Jump to content

Rep:Mod:Wlt113

From ChemWiki

Introduction

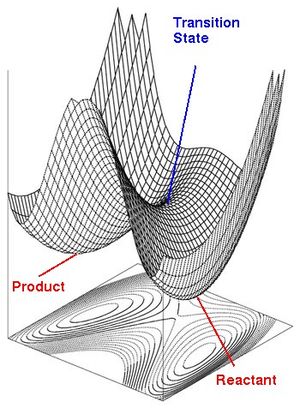
Much of chemical kinetics today is fundamentally based upon transition state theory (TST), which postulates that the transition state is a theoretical high-energy state that reacting molecules can attain.[1] Mathematically, it is a type of stationary point, and as shown in Figure 1, can appear as either a maximum point in a 1-dimensional (1D) plot, or a saddle point in a 2-dimensional potential energy surface (PES) plot.[1] The saddle point in the 2D PES divides the stable potential wells of the reactants and products, and represents a dividing surface where there is only one direction to proceed in without elevating the system's energy. In addition, the reaction coordinate taken in the 1D plot often represents the minimum energy path (MEP) in the 2D PES leading from the reactants to the products.[1]


Figure 1: (a) 1D Reaction Profile and (b) 2D PES.[2]
(a) (b)


Using computational methods, it is possible to calculate and compare the energies of the reactants, transition state and products, and assess the reactivity of various pathways for a reaction by comparing activation energies and reaction free energy changes or reaction energies. In this work, using the computational software Gaussian at the semi-empirical PM6 and hybrid functional density functional theory (DFT) method B3LYp/6-31G(d),[3] the transition states of several Diels-Alder reactions are investigated to shed insight on the kinetics and thermodynamics of the pathways possible, taking into account stereoelectronic effects where relevant.

Nf710 (talk) 22:26, 8 March 2017 (UTC) You have shown a fairly good understanding here. However you should have talked about the TS and minima in terms of second derivatives.

Exercise 1: Reaction of Butadiene with Ethene

Reaction Scheme


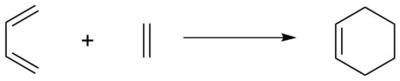
In this exercise, the Diels-Alder cycloaddition between butadiene and ethene was studied, and the transition state optimized using Gaussian at the PM6 level. Links to the calculation output for the optimized structures of butadiene,[4] ethene,[5] cyclohexene,[6] the transition state,[7] and the intrinsic reaction coordinate (IRC)[8] can be found in References.


Orbital Symmetry-controlled Overlap of Frontier MOs of Butadiene and Ethene

The reactivity of the reactants in a Diels-Alder cycloaddition can be rationalized using frontier molecular orbital (FMO) theory.[9] As shown in Figure 2, the highest occupied molecular orbitals (HOMOs) and lowest unoccupied molecular orbitals (LUMOs) of ethene and butadiene can overlap to form key FMOs in the transition state and resultant cyclohexene product. An MO can be symmetric (having a plane of symmetry) or antisymmetric (lacking a plane of symmetry), and as shown in the MO diagram, the symmetry requirements in such a reaction are that reactant MOs of the same symmetry must interact for the orbital overlap to be non-zero. The overlap integrals for the three possible cases where reactant MOs can be either symmetric or antisymmetric are shown below (Table 2). These results are consistent with the Woodward-Hoffmann rules for pericyclic reactions (Figure 3), which predicts that the reaction is thermally allowed whether the HOMO of butadiene overlaps with the LUMO of ethene (normal electron-demand Diels-Alder reaction) or the HOMO of ethene overlaps with the LUMO of butadiene (inverse electron-demand).[10] Since there is significant overlap in both cases, this system may be considered an example of a neutral Diels-Alder reaction [11]


Figure 2: MO diagram showing overlap of FMOs of Ethene and Butadiene to form FMOs in the Diels-Alder transition state (shown in Table 1). MOs can be either symmetric (S) or asymmetric (AS).

(Fv611 (talk) 13:15, 6 March 2017 (UTC) Very good MO diagram.)


Table 1: FMOs of the Diels-Alder Transition State between Butadiene and Ethene. (N.A. = Not Applicable.)
MO Butadiene Ethene Cyclohexene
LUMO+1 N.A. N.A.
LUMO
HOMO
HOMO-1 N.A. N.A.


Table 2: Overlap Integrals for Interaction of Symmetric and/or Antisymmetric Reactant MOs
Symmetries of Reactant MOs Overlap Integral Reaction allowed?
Symmetric-Symmetric Non-zero Allowed
Symmetric-Antisymmetric Zero Forbidden
Antisymmetric-Antisymmetric Non-zero Allowed

(Fv611 (talk) 13:15, 6 March 2017 (UTC) Could have discussed this instead of just giving a table.)

Figure 3: Suprafacial-suprafacial overlap of (a) the HOMO of Butadiene with the LUMO of Ethene, and; (b) the HOMO of Ethene with the LUMO of Butadiene


Variation in C-C Bond Lengths with Reaction Coordinate

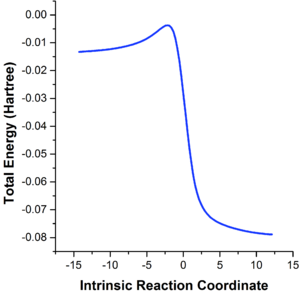
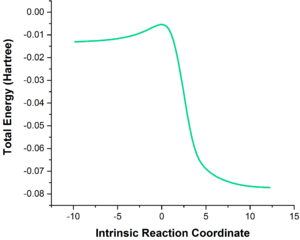
The lengths of the C-C bonds within reactant molecules vary continuously with reaction coordinate, as shown in Figure 4, which was obtained via an intrinsic reaction coordinate (IRC) calculation that is based on following the MEP from reactants to products. The computed C-C bond lengths within the reactants, transition state and product are tabulated in Table 3.

The C1-C6 and C4-C5 bonds (1.33 Å) are initially slightly shorter than the typical sp2-sp2 C=C double bond length (1.34 Å) in butadiene, due to π-conjugation, but subsequently surpasses 1.34 Å and increases to 1.37 Å in the transition state, ultimately becoming single bonds (1.50 Å) in the cyclohexene product with the typical sp2-sp3 C-C bond length (1.50 Å).[12] The C4-C5 bond is initially a typical sp2-sp2 C-C bond (1.47 Å), but decreases in length in the transition state (1.41 Å), until it reaches a typical sp2-sp2 C=C bond.[12]

The C2-C3 C=C bond in ethene (1.33 Å) is slightly shorter than the typical sp2-sp2 C=C bond length; as the reaction progresses, it lenghthens to being intermediate to typical sp2-sp2 and sp3-sp3 C-C bond lengths (1.38 Å), and eventually becomes a typical sp3-sp3 C-C bond.[12]

Within the transition state, the C1-C2 and C3-C4 bond length of 2.11 Å is intermediate between a typical sp3-sp3 C-C bond (1.54 Å)[12] and the sum of Van der Waals (VDW) radii for two carbon atoms (3.40 Å).[13] The distance between two atoms being under the sum of their VDW radii is the indication of a bonding interaction, which is the case of the two partially formed C1-C2/C3-C4 bonds in the transition state.

Table 3: C-C Bond Distances in the Butadiene and Ethene Reactants, the Transition State, and the Cyclohexene Product. (N.A. = Not Applicable.)
Butadiene Ethene Transition State Cyclohexene
C1-C2 N.A. N.A. 2.11 1.54
C2-C3 N.A. 1.33 1.38 1.53
C3-C4 N.A. N.A. 2.11 1.54
C4-C5 1.33 N.A. 1.38 1.50
C5-C6 1.47 N.A. 1.41 1.34
C1-C6 1.33 N.A. 1.38 1.50


Figure 4: Plot showing Variation in C-C Bond Distances with Reaction Coordinate.


Visualization of Reaction Coordinate

As shown in Figure 5, corresponding to the vibration with an imaginary frequency of 948.83i cm-1, formation of the two C-C bonds between butadiene and ethene in the transition state is a synchronous and concerted process, as expected for the symmetrical system where two equivalent C-C bonds are formed.


Figure 5: Front and Side Views of the Vibration corresponding to the Reaction Path at the Transition State.
Front View Side View

Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole

Reaction Scheme

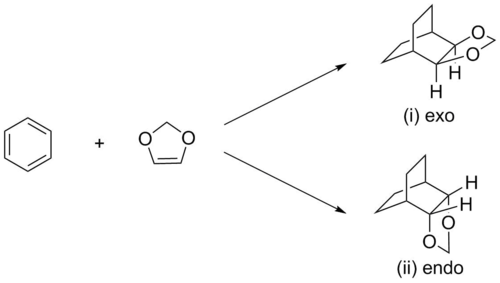
(You're missing the distinguishing double bonds in the products Tam10 (talk) 12:51, 8 March 2017 (UTC))

In this exercise, the Diels-Alder reaction between the electron-rich dienophile 1,3-dioxole and the diene cyclohexadiene was studied, and the transition state was initially optimized at PM6, before being reoptimized at the B3LYP/6-31G(d) level of theory. Links to the calculation output for the PM6 and B3LYP/6-31G(d)-optimized structures of cyclohexadiene,[14] [15] 1,3-dioxole,[16] [17] the exo product,[18] [19] the endo product,[20] [21] the exo transition state,[22] [23] the endo transition state,[24] [25] and the intrinsic reaction coordinate (IRC) of the exo pathway[26] [27] and endo pathway[28][29] can be found in References.


Overlap of FMOs of Cyclohexadiene and 1,3-Dioxole

The orbital symmetry-controlled overlap of reactant FMOs are shown in Figure 6. This is an example of an inverse electron-demand Diels-Alder reaction as the HOMO in the system is that of the 1,3-dioxole dienophile, whereas the LUMO is contributed by cyclohexadiene.


Figure 6: MO diagram showing overlap of FMOs of 1,3-Dioxole and Cyclohexadiene to form FMOs in the exo and endo Diels-Alder transition state (shown in Table 4).
Exo Endo


Table 4: FMOs of the (a) exo and (b) endo Diels-Alder Transition State between 1,3-Dioxole and Cyclohexadiene
MO Graphic Representation of exo MOs Graphic Representation of endo MOs
LUMO+1
LUMO
HOMO
HOMO-1


Kinetics and Thermodynamics of Reaction Pathways

The activation energies and reaction enthalpies for the formation of the exo and endo adducts respectively were calculated by taking differences in the values of Sum of electronic and thermal Free energy obtained for the reactants, transition state and products through Gaussian (Table 5). It was found that the endo product was both the kinetically (lower activation energy) and thermodynamically (larger, more negative reaction enthalpy) favoured product, as compared to the exo product.


Table 5: Computed Energies (EH), Activation Energies (kJ mol-1) and Reaction Enthalpies (kJ mol-1) for the Exo and Endo Adducts, at 298.15 K.
Computed Energy of Species (EH) Activation Energy (kJ mol-1) Reaction Energy (kJ mol-1)
Reactants Cyclohexadiene -233.324375 N.A. N.A.
1,3-Dioxole -267.068643
Sum of Reactant Energies -500.393018
Transition State Exo -500.285411 282.52 N.A.
Endo -500.332149 159.81
Product Exo -500.417322 N.A. -63.81
Endo -500.418692 -67.41


Nf710 (talk) 22:34, 8 March 2017 (UTC) Your activation energies are incorrect for the exo you used the Sum of electronic and thermal Energies rather than Sum of electronic and thermal free Energies. This is a shame as your energy of reaction is correct for both.

Secondary Orbital Interactions and Steric Factors influencing Stereoselectivity in the Transition State

The lower activation energy for endo product formation can be explained by secondary orbital interactions. As shown in Table 6, the p-orbital coefficients on the oxygen atoms are of the correct phase to and can overlap with the orbital coefficients on the diene carbon atoms not directly involved in bond formation. In addition, in the exo transition state, the steric repulsion non-reacting atoms of the reactants (as illustrated in Table 6) is destabilizing. Hence, both electronic and steric factors favour the endo transition state, leading to the computed kinetic and thermodynamic stereoselectivity. The steric clash within the exo geometry also raises the energy of the exo product, leading to the endo product being the thermodynamically favoured one.


Table 6: Primary and Secondary Orbital Interactions between 1,3-Dioxole and Cyclohexadiene in the Diels-Alder Transition State. (Primary bonding interactions are shown as black dashed lines, whereas secondary orbital interactions are shown as red dashed lines.)
Exo Endo
MO Graphic
Computed MO

Nf710 (talk) 22:40, 8 March 2017 (UTC) Very good section. Nice diagrams explaining all your points. Shame you got the exo activation energy wrong.

Exercise 3: Comparing the Diels-Alder and Cheletropic Reactions between o-Xylylene and SO2

Reaction Scheme

In this final exercise, the expected exo and endo hetero-Diels-Alder reaction pathways, the alternative exo and endo Diels-Alder reaction, and the cheletropic reaction pathway between the electron-deficient dienophile SO2 and the electron-rich diene o-xylylene are compared by optimization of the corresponding reactants, transition states and products at the PM6 level. Links to the calculation output for the optimized structures of o-xylylene, [30] SO2, [31] the exo,[32] and endo[33] product for the expected Diels-Alder reaction, the cheletropic product,[34] the exo, [35] and endo product [36] for the alternative Diels-Alder reaction, the exo [37] and endo [38] transition state for the expected Diels-Alder reaction, the cheletropic transition state,[39] the exo[40] and endo[41] transition states for the alternative Diels-Alder reaction, and the intrinsic reaction coordinate (IRC) of the exo[42] and endo[43] pathways of the expected Diels-Alder reaction, and the cheletropic[44] pathway can be found in References.

An analysis of reactant FMO overlap has not been included in this Exercise: it is expected that similar overlaps exist here between the archetypal diene fragment and dienophile fragments, and secondary orbital and/or steric interactions in the transition state can be used to rationalize relative activation energies and whether the endo or exo Diels-Alder adduct is kinetically favoured. It is also expected that this system behaves like a normal electron-demand Diels-Alder reaction, considering that the diene has electron-donating alkyl substituents, whereas the dienophile contains electronegative oxygen atoms and electron-withdrawing S=O functioncal groups.

Visualization of Reaction Coordinate

The IRCs were calculated and illustrated for the exo and endo pathways of the expected Diels-Alder reaction, and the cheletropic reaction. As shown in Table 6, the formation of two new bonds is asynchronous with both Diels-Alder reactions (with formation of the C-O bond slightly faster than that of the C-S bond), but synchronous in the cheletropic reaction (where both C-S bonds form simultaneously). In addition, the o-xylylene fragment appears to aromatize and form an aromatic 6-membered ring with delocalization extending to the carbon atoms outside the ring, which suggests that o-xylylene reacts as a diradical in the transition state. This would be due to the aromatic driving force and the inherent instability of o-xylylene.

Table 6: Illustration of Bond Formation in the Transition State and Plot of Energy against IRC for the formation of the (a) exo and (b) endo Diels-Alder adducts and (c) the Cheletropic adduct.
(a) Exo (b) Endo (c) Cheletropic
Illustration of Bond Formation
Plot of Energy against IRC


Kinetics and Thermodynamics of Reaction Pathways

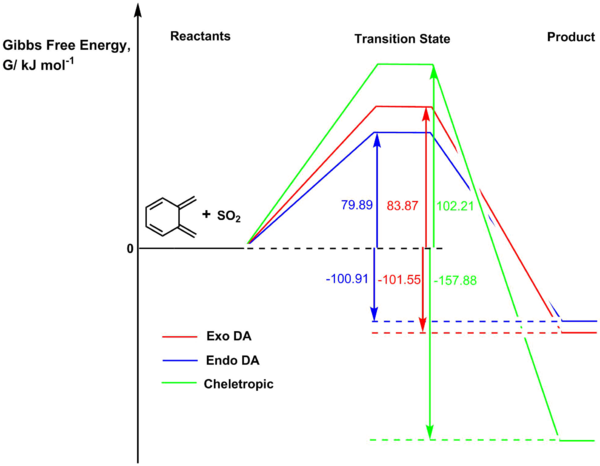
Analysis of activation energies and reaction energies (Table 7) revealed that for the expected Diels-Alder reaction, the endo product is the kinetic product and the exo product is the thermodynamic product, but overall, taking the chelotropic reaction into account, the chelotropic product is the thermodynamically favoured product (largest, most negative reaction energy) whereas the endo Diels-Alder product is the kinetic product (lowest activation energy). This suggests that if a mixture of o-xylylene and SO2 were allowed to react, the endo Diels-Alder product would be the fastest-formed, but if left to equilibrate, the product mixture will feature the cheletropic adduct as the major product; this result is consistent with literature observations and computations.[45] The reaction profile of all three pathways is illustrated in Figure 7.

Table 7: Computed Energies (EH), Activation Energies (kJ mol-1) and Reaction Energies (kJ mol-1) for the Exo and Endo Diels-Alder, and Cheletropic reaction adducts, at 298.15 K.
Computed Energy of Species (EH) Activation Energy (kJ mol-1) Reaction Energy (kJ mol-1)
Reactants o-Xylylene 0.178746 N.A. N.A.
SO2 -0.118614
Sum of Reactant Energies 0.060132
Transition State Exo 0.092077 83.87 N.A.
Endo 0.090559 79.89
Cheletropic 0.099062 102.21
Product Exo 0.021454 N.A. -101.55
Endo 0.021696 -100.91
Cheletropic -0.000001 -157.88


Figure 7: Reaction Profile Diagram for the Three Possible Reaction Pathways.


Diels-Alder Cycloaddition involving an Alternative Diene in o-Xylylene

As indicated in the Reaction Scheme, o-Xylylene contains a second diene fragment in an s-cis configuration, and the reactivity of this fragment in an alternative Diels-Alder reaction via the exo and endo pathways was examined by computation of the corresponding activation energies and reaction energies. As shown in Table 9, the kinetically favoured product is the endo product, and the thermodynamically favoured product is the exo product. However, the activation energies for both pathways are higher than their counterparts' in the previous Diels-Alder reaction, and the reaction enthalpies are both endothermic, as opposed to the exothermic reaction energies for the previous Diels-Alder reaction. Hence, this alternative Diels-Alder reaction is both kinetically and thermodynamically disfavoured with respect to the previous one discussed.


Table 9: Computed Energies (EH), Activation energies (kJ mol-1) and Reaction Energies (kJ mol-1) for the AlternativeExo and Endo Diels-Alder Reaction Pathways, at 298.15 K.
Computed Energy of Species (EH) Activation Energy (kJ mol-1) Reaction Energy (kJ mol-1)
Transition State Exo 0.105057 117.95 N.A.
Endo 0.102071 110.11
Product Exo 0.067304 N.A. 18.83
Endo 0.065609 14.38

Conclusion

In conclusion, the reactivity of the Diels-Alder reactions between the diene/dienophile systems, butadiene/ethene (Exercise 1), cyclohexadiene/1,3-dioxole (Exercise 2), and o-xylylene/SO2 (Exercise 3), were investigated via calculations on Gaussian software, and the reactants, transition state structures and products were optimized at PM6 (Exercise 1 and 3) and B3LYP/6-31G(d) (Exercise 2) levels of theory. IRC calculations were used to illustrate the reaction coordinate, and the type of Diels-Alder reaction (normal or inverse electron-demand) was determined from analysis of overlapping reactant FMOs. The activation energies and reaction energies were calculated to establish the kinetically and thermodynamically favoured reaction pathways, and the involvement of secondary orbital interactions and sterics was used to explain the lower activation energy for the formation of the kinetically favoured endo product for the cyclohexadiene/1,3-dioxole system (Exercise 2). Finally, optimized transition state structures with different sites of reaction were obtained, and used to determine regioselectivity in a system with more than one diene functional group (Exercise 3).

References

  1. ↑ 1.0 1.1 1.2 P. Pechukas, "Transition state theory.", Annual Review of Physical Chemistry, 1981, 32, 159-177.DOI:10.1146/annurev.pc.32.100181.001111
  2. ↑ "2-Dimensional Potential Energy Surface." Taken from: http://211.81.50.59//education/OCPkb/module2.php
  3. ↑ A. D. Becke, "A new mixing of Hartree–Fock and local density‐functional theories", J. Chem. Phy., 1993, 98, 1372.DOI:10.1063/1.464304
  4. ↑ "PM6-optimized Structure of Butadiene." https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:WLT_EXERCISE_1_BUTADIENE_MOS_OPT.LOG
  5. ↑ "PM6-optimized Structure of Ethene." https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:WLT_EXERCISE_1_ETHENE_MOS_OPT.LOG
  6. ↑ "PM6-optimized Structure of Cyclohexene." https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:WLT_EXERCISE_1_CYCLOHEXENE_OPT.LOG
  7. ↑ "PM6-optimized Transition State Structure for Exercise 1." https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:WLT_EXERCISE_1_CYCLOHEXENE_FROZEN_TS_MOS_OPT.LOG
  8. ↑ "Intrinsic Reaction Coordinate (IRC) for Exercise 1." https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:WLT_EXERCISE_1_CYCLOHEXENE_FROZEN_TS_IRC.LOG
  9. ↑ K. Fukui, T. Yonezawa, and H. Shingu, "Molecular Orbital Theory of Reactivity in Aromatic Hydrocarbons", J. Chem. Phy., 1952, 20, 722.DOI:10.1063/1.1700243
  10. ↑ F. A. Carey, R. J. Sundberg. (2007). "Advanced Organic Chemistry: Part A: Structures and Mechanisms (5th ed.)", New York: Springer. ISBN 978-0-387-44899-2
  11. ↑ G. Hilt, K. I. Smolko, B. V. Lotsch, "Cobalt(I)-catalyzed Neutral Diels-Alder Reactions of Oxygen-functionalized Acyclic 1,3-Dienes with Alkynes", Synlett, 2002, 7, 1081-1084.DOI:10.1063/1.1700243
  12. ↑ 12.0 12.1 12.2 12.3 J. Clayden, N. Greeves, S. Warren, P. Wothers. (2001). "Organic Chemistry (2nd ed.)", OUP Oxford. ISBN 978-0-19-927029-3
  13. ↑ S. S. Batsanov. "Van der Waals Radii of Elements", Inorganic Materials, 2001, 37, 871-885.DOI:10.1023/A:1011625728803
  14. ↑ "PM6-optimized Structure of Cyclohexadiene." https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:WLT_EXERCISE_2_CYCLOHEXADIENE_REACTANT_SYMMETRY_BROKEN.LOG
  15. ↑ "B3LYP/6-31G(d)-optimized Structure of Cyclohexadiene." https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:WLT_EXERCISE_2_CYCLOHEXADIENE_REACTANT_SYMMETRY_BROKEN_B3LYP_6-31G(D)_OPT.LOG
  16. ↑ "PM6-optimized Structure of 1,3-Dioxole." https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:WLT_EXERCISE_2_DIOXOLE_REACTANT_OPT.LOG
  17. ↑ "B3LYP/6-31G(d)-optimized Structure of 1,3-dioxole." https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:WLT_EXERCISE_2_DIOXOLE_REACTANT_SYMMETRY_BROKEN_B3LYP_6-31G(D)_OPT.LOG
  18. ↑ "PM6-optimized Structure of the Exo Product for Exercise 2." https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:WLT_EXERCISE_2_EXO_PRODUCT_OPT.LOG
  19. ↑ "B3LYP/6-31G(d)-optimized Structure of the Exo Product for Exercise 2." https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:WLT_EXERCISE_2_EXO_PRODUCT_B3LYP_6-31G(D)_OPT.LOG
  20. ↑ "PM6-optimized Structure of the Endo Product for Exercise 2." https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:WLT_EXERCISE_2_ENDO_PRODUCT_OPT.LOG
  21. ↑ "B3LYP/6-31G(d)-optimized Structure of the Endo Product for Exercise 2." https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:WLT_EXERCISE_2_ENDO_PRODUCT_B3LYP_6-31G(D)_OPT.LOG
  22. ↑ "PM6-optimized Exo Transition State Structure for Exercise 2." https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:WLT_EXERCISE_2_EXO_PRODUCT_FROZEN_TS_OPT.LOG
  23. ↑ "B3LYP/6-31G(d)-optimized Exo Transition State Structure for Exercise 2." https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:Wlt_exercise_2_exo_product_frozen_TS_B3LYP_6-31G(d)_MO_opt.log
  24. ↑ "PM6-optimized Endo Transition State Structure for Exercise 2." https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:WLT_EXERCISE_2_ENDO_PRODUCT_FROZEN_TS_OPT.LOG
  25. ↑ "B3LYP/6-31G(d)-optimized Endo Transition State Structure for Exercise 2." https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:Wlt_exercise_2_endo_product_frozen_TS_B3LYP_6-31G(d)_MO_opt.log
  26. ↑ "PM6-optimized Intrinsic Reaction Coordinate (IRC) for Exo Transition State in Exercise 2." https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:WLT_EXERCISE_2_EXO_PRODUCT_FROZEN_TS_IRC_RECORRECT_NEVER.LOG
  27. ↑ "B3LYP/6-31G(d)-optimized Intrinsic Reaction Coordinate (IRC) for Exo Transition State in Exercise 2." https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:WLT_exercise_2_exo_product_frozen_TS_B3LYP_6-31G(d)_IRC.log
  28. ↑ "PM6-optimized Intrinsic Reaction Coordinate (IRC) for the Endo Transition State in Exercise 2." https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:WLT_EXERCISE_2_ENDO_PRODUCT_FROZEN_TS_IRC.LOG
  29. ↑ "B3LYP/6-31G(d)-optimized Intrinsic Reaction Coordinate (IRC) for the Endo Transition State in Exercise 2." https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:WLT_exercise_2_endo_product_frozen_TS_B3LYP_6-31G(d)_IRC.log
  30. ↑ "PM6-optimized Structure of o-Xylylene." https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:WLT_EXERCISE_3_DIENE_REACTANT_OPT.LOG
  31. ↑ "PM6-optimized Structure of Sulfur Dioxide." https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:WLT_EXERCISE_3_SO2_REACTANT_OPT.LOG
  32. ↑ "PM6-optimized Structure of the Exo Product from the Expected Diels-Alder Reaction for Exercise 3." https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:WLT_TUTORIAL_METHOD_3_XYLYLENE-SO2_OPT.LOG
  33. ↑ "PM6-optimized Structure of the Endo Product from the Expected Diels-Alder Reaction for Exercise 3." https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:WLT_EXERCISE_3_ENDO_PRODUCT_OPT.LOG
  34. ↑ "PM6-optimized Structure of the Cheletropic Product for Exercise 3." https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:WLT_EXERCISE_3_CHELETROPIC_PRODUCT_OPT.LOG
  35. ↑ "PM6-optimized Structure of the Exo Product from the Alternative Diels-Alder Reaction for Exercise 3." https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:WLT_EXERCISE_3_OTHER_DA_EXO_PRODUCT_OPT.LOG
  36. ↑ "PM6-optimized Structure of the Endo Product from the Alternative Diels-Alder Reaction for Exercise 3." https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:WLT_EXERCISE_3_OTHER_DA_ENDO_PRODUCT_OPT.LOG
  37. ↑ "PM6-optimized Transition State Structure of the Exo Pathway of the Expected Diels-Alder Reaction for Exercise 3." https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:WLT_TUTORIAL_METHOD_3_XYLYLENE-SO2_FROZEN_TS_OPT.LOG
  38. ↑ "PM6-optimized Transition State Structure of the Endo Pathway of the Expected Diels-Alder Reaction for Exercise 3." https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:WLT_XYLELENE-SO2_ENDO_POSTFROZEN_TS_OPT.LOG
  39. ↑ "PM6-optimized Transition State Structure of the Cheletropic Pathway of the Expected Diels-Alder Reaction for Exercise 3." https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:WLT_EXERCISE_3_CHELETROPIC_FROZEN_TS_OPT.LOG
  40. ↑ "PM6-optimized Exo Transition State Structure of the Alternative Diels-Alder Reaction for Exercise 3." https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:WLT_EXERCISE_3_OTHER_DA_EXO_POSTFROZEN_TS_OPT.LOG
  41. ↑ "PM6-optimized Endo Transition State Structure of the Alternative Diels-Alder Reaction for Exercise 3." https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:WLT_EXERCISE_3_OTHER_DA_ENDO_POSTFROZEN_TS_OPT.LOG
  42. ↑ "Intrinsic Reaction Coordinate (IRC) of the Exo Pathway of the Expected Diels-Alder Reaction for Exercise 3." https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:WLT_TUTORIAL_METHOD_3_XYLYLENE_SO2_TS_IRC.LOG
  43. ↑ "Intrinsic Reaction Coordinate (IRC) of the Exo Pathway of the Expected Diels-Alder Reaction for Exercise 3." https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:WLT_XYLELENE-SO2_ENDO_POSTFROZEN_TS_IRC.LOG
  44. ↑ "Intrinsic Reaction Coordinate (IRC) of the Cheletropic Reaction Pathway for Exercise 3." https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:WLT_EXERCISE_3_CHELETROPIC_FROZEN_TS_IRC.LOG
  45. ↑ D. Suarez, T. L. Sordo, J. A. Sordo, "A Comparative Analysis of the Mechanisms of Cheletropic and Diels-Alder Reactions of 1,3-Dienes with Sulfur Dioxide: Kinetic and Thermodynamic Controls", J. Org. Chem., 1995, 60, 2848-2852.DOI:10.1021/jo00114a039
Retrieved from "https://chemwiki.ch.ic.ac.uk/index.php?title=Rep:Mod:Wlt113&oldid=818214"