Jump to content

Rep:Mod:WhatWentWong

From ChemWiki

Computational Chemistry Laboratory: Module 3

By Eugene Wong

Reaction kinetics are an important aspect of chemical reactivity, as they help to explain phenomena that thermodynamic data fails to predict. In synthetic chemistry, the major product of a reaction may not always be the most stable, and this is more often than not attributed to a lowered transition state energy (and thus activation energy barrier) for that product, which leads to it being formed faster. In this module, transition states will be studied extensively in order to reproduce the correlation between experimentally observed "kinetic" major products and their lower activation energy barriers.

Cope Rearrangement

The Cope Rearrangement, named after Arthur Cope[1], is a pericyclic, [3,3]-sigmatropic rearrangement which is specific for 1,5-dienes. In this section, ten conformers of 1,5-hexadiene, as well as a boat transition state (TS) and a chair TS will be studied using two different levels of theory (HF/3-21G & DFT/B3LYP/6-31G*). This is done in order to gain a better understanding of the mechanistic pathway for the Cope Rearrangement. Figure 1 below depicts the reaction mechanism, and the two possible transition states leading to the product.

Figure 1 - Mechanism for the Cope rearrangement

Optimisation of 1,5-Hexadiene Conformers

A total of ten different "Anti-" and "Gauche-" conformers were optimised to a minimum using the HF/3-21G level of theory. (Anti- and "Gauche-" refer to the conformational arrangement of the 4 central sp3 C-H bonds: "Anti-" being the case where both H-C-C-H dihedral angles are 180o; and "Gauche-" being the case with one 180o H-C-C-H dihedral angle and the remaining H-C-C-H having a dihedral angle of 60o. The molecules were also symmetrised. The following Table 1 lists the optimised energies and symmetries of the ten conformers:

Table 1: Optimised (HF/3-21G) Data for 1,5-Hexadiene Conformers
Conformer Total Energy (Hartrees) Relative Energy (Kcal mol-1) Point Group
Anti (1) [2] -231.69260 +0.04 C2
Anti (2) [3] -231.69254 +0.08 Ci
Anti (3) [4] -231.68907 +2.25 C2h
Anti (4) [5] -231.69097 +1.06 C1
Gauche (1) [6] -231.68722 +3.10 C2
Gauche (2) [7] -231.69167 +0.62 C2
Gauche (3) [8] -231.69266 0.00 C1
Gauche (4) [9] -231.69153 +0.71 C2
Gauche (5) [10] -231.68962 +1.91 C1
Gauche (6) [11] -231.68916 +2.20 C1

Of these ten conformers, the lowest three in energy (Anti(1), Anti(2) and Gauche(3)) were re-optimised at the DFT/B3LYP/6-31G* level in order to analyse the differences in optimisation from each of the different levels of theory. The results are summarised in the following Table 2:

Table 2: Optimised (DFT/B3LYP/6-31G*) Data for 1,5-Hexadiene Conformers
Conformer Total Energy (Hartrees) Relative Energy (Kcal mol-1) Point Group
Anti (1) [12] -234.61179 0 C2
Anti (2) [13] -234.61171 +0.05 Ci
Gauche (3) [14] -234.61133 +0.29 C1

Comparison of Optimisation Results from Both Theory Levels

(Please see the annotated Jmol files in Tables 1 & 2)

The different levels of theory employed only lead to slight differences in optimised dihedral angle measurements. The more striking difference, however, is attributed to the minimisation energies. DFT/B3LYP/6-31G* gives optimisation energies which are approximately 3 Eh more negative than those observed for HF/3-21G. An explanation for this is the larger basis set (6-31G*) employed for the B3LYP method, which takes into account stabilising stereoelectronic effects, such as σ(C-H) → σ*(C-C) donation. The Anti(1) conformer is shown to be the most stable conformer from the DFT/B3LYP/6-31G* level, as opposed to the Gauche(3) conformer from HF/3-21G. This is most probably due to a higher extent of the aforementioned σ(C-H) → σ*(C-C) donation being observed for the Anti(1) conformer, as the Gauche(3) conformer displays higher deviations from anti-periplanar H-C-C-C dihedral angles, and experiences a lower extent of σ(C-H) → σ*(C-C) orbital overlap.

IR Frequency Analyses (DFT/B3LYP/6-31G*)

Frequency analyses were run on the three lowest energy conformers, after their optimisation at the DFT/B3LYP/6-31G* level of theory. Each of the three conformers display two C=C stretches (symmetric and antisymmetric). Tables 3 to 5 display these stretching modes:

Table 3 - IR Data[15] for Anti(1) conformer.
Vibrational Mode Absorption Intensity Bond Frequency (cm-1) Diagram
Symmetric C=C stretch 5 1732
Asymmetric C=C stretch 14 1735
Table 4 - IR Data[16] for Anti(2) conformer.
Vibrational Mode Absorption Intensity Bond Frequency (cm-1) Diagram
Symmetric C=C stretch 0 1731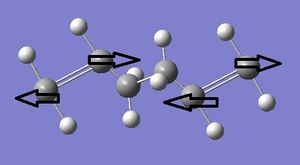
Asymmetric C=C stretch 18 1734
Table 5 - IR Data[17] for Gauche(3) conformer.
Vibrational Mode Absorption Intensity Bond Frequency (cm-1) Diagram
Symmetric C=C stretch 7 1732
Asymmetric C=C stretch 6 1733

It can be observed from these that the symmetry of the compound plays a large role in determining the number of IR active modes, as well as their intensity. The Anti(2) conformer (Ci symmetry), for instance, has the largest dipole moment change caused by an antisymmetric C=C stretch, but its symmetric C=C stretch causes no change in dipole moment, and is hence inactive. The other two conformers experience dipole moment changes upon both symmetric and antisymmetric C=C stretching, and thus have two active C=C IR modes each.

Thermochemical Data

The thermochemical data was obtained from the log files[15],[16],[17] for the frequency calculations: 

Anti(1)
_________________________________________________________________________________

 Sum of electronic and zero-point Energies=           -234.469298
 Sum of electronic and thermal Energies=              -234.461966
 Sum of electronic and thermal Enthalpies=            -234.461022
 Sum of electronic and thermal Free Energies=         -234.500862


Anti(2)
_________________________________________________________________________________

 Sum of electronic and zero-point Energies=           -234.469204
 Sum of electronic and thermal Energies=              -234.461857
 Sum of electronic and thermal Enthalpies=            -234.460913
 Sum of electronic and thermal Free Energies=         -234.500777


Gauche(3)
_________________________________________________________________________________

 Sum of electronic and zero-point Energies=           -234.468693
 Sum of electronic and thermal Energies=              -234.461464
 Sum of electronic and thermal Enthalpies=            -234.460520
 Sum of electronic and thermal Free Energies=         -234.500105

The data can be summarised as follows:

The first term, "Sum of electronic and zero-point Energies" is computed at T=0K, while the other three are taken at T=298.15K and P=1atm.

The second term, "Sum of electronic and thermal Energies", includes rotational, vibrational and electronic degrees of freedom.

The third term, "Sum of electronic and thermal Enthalpies", includes an additional RT correction for convertion of potential energy into enthalpy (c.f. second term).

Lastly, the fourth term, "Sum of electronic and thermal Free Energies", includes a contribution from entropy to obtain the free energy of the system at 298.15K. (G = H - TS)

It is shown that while the first three terms differ by no more than approximately 0.008 Eh (5 kcal mol-1), the fourth term for free energy is about 0.04 Eh (25 kcal mol-1) more negative than all of them. This shows that the contribution from the entropy of the system is about 5 times as high as the other degrees of freedom, which is not a trivial amount.

Given more time, calculations at varying temperatures can be done using the "Freq=ReadIsotopes" option in Gaussian. It is understood that at 0K, all the four terms will give the same value, due to the absence of temperature dependent terms, while at higher temperature values (i.e. 500K), the difference between the four values will increase, with the difference being much more pronounced for the free energy term (as compared with the other values), due to the higher numerical value for entropy (TS > RT).

Chair Transition State (HF/3-21G)

Optimisation and Frequency Calculations

Berny TS Calculations

The C2v-symmetric chair transition state[18] (see Figure 1) was optimised, via a "guess structure" involving two optimised allyl fragments[19], with the initial terminal C to terminal C distance set at 2.2Å. The level of theory used for these optimisations was HF/3-21G, and Gaussian was configured to calculate the frequencies (Opt+Freq) for the TS(Berny) as well.

The optimised TS shows that the terminal C to terminal C distance is ideally 2.02Å (see annotated Jmol file above). The optimisation energy from this level of theory was given to be -231.61932 Eh.

An imaginary frequency of -818 cm-1 was obtained from the frequency calculations, and this is characteristic of an optimised TS. The mode of vibration also corresponds to the formation of the product in the Cope Rearrangement, as seen in the following animation:

Figure 2: Chair TS imaginary frequency
Frozen Reaction Coordinate Method

An alternative approach to obtaining the TS was carried out by freezing the bonding reaction coordinate involving the terminal C atoms of each allyl fragment (using the Redundant Coordinate Editor in Gaussview), which had the effect of restricting any bond breaking or forming between these terminal C atoms. The system was then optimised [20] (HF/3-21G) to a minimum. This pre-optimised file was then edited with Gaussview's Redundant Coordinate Editor to allow for the "adding" of "bonds" between the previously frozen terminal C atoms, prior to TS(Berny) optimisation[21]. The results of this optimisation match those seen in the previous section, with the same bond breaking/forming distances of 2.02Å, and energy of -231.61932 Eh. (See annotated Jmol file, below)

Boat Transition State (HF/3-21G)

QST2 Optimisation and Frequency Calculations

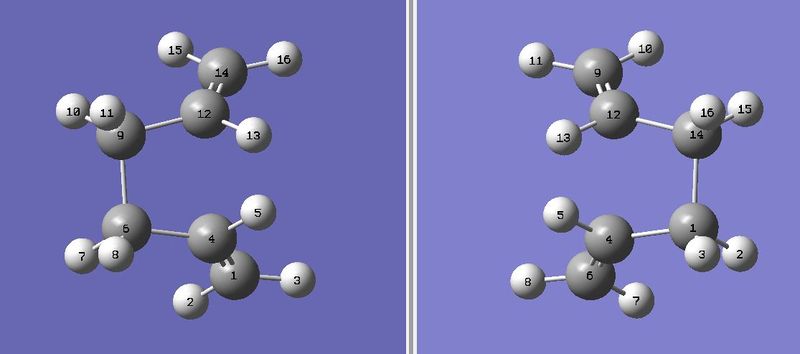
For the optimisation of the boat TS, the QST2 calculation method was used, in order to interpolate between the reactant and product structures and locate a TS. Special attention was paid to the numbering of the C and H atoms in the reactant and product, in order to show that the difference in the initial and final states was due to a rearrangement of the allyl fragments and not just a simple reorientation of the whole molecule. The atom numbering as follows:

Figure 3: Initial QST2 Reactant and Product Configurations

The first QST2 attempt[22] was shown to have failed due to the initial and final states not being close enough to the TS in terms of geometry. The Gaussian job file was edited as neccessary: The central dihedral C4-C6-C9-C12 angles were reduced to 0o, and the inner C4-C6-C9 and C6-C9-C12 bond angles were reduced to 100o, prior to resubmission:

Figure 4: 2nd QST2 Reactant and Product Configurations

The second QST2 attempt[23] was successful, and resulted in a TS with 2.14Å bond breaking/forming distances and energy of -231.60280 Eh. (See annotated Jmol file below)

This optimised TS structure was further confirmed by an imaginary frequency of -840 cm-1, which corresponds to the bond forming and bond breaking motion of the reaction.

Figure 5: Boat TS imaginary frequency

Intrinsic Reaction Coordinate Calculations (HF/3-21G)

This section details the use of the Intrinsic Reaction Coordinate (IRC) method as a means of following the TS structure, on the potential energy surface, down towards a local minimum, which represents the reactant/product structure.

From Chair TS to Product

An IRC calculation[24] was carried out on the HF/3-21G optimised chair TS, with 50 points to be plotted, in the forward direction (only the forward direction was required due to the symmetrical nature of the reaction profile).

The Gaussian job was shown to have stopped after 26 iterations, but this was nonetheless sufficient to obtain a reaction profile diagram, which begins from the TS and proceeds towards the product:

Figure 6: IRC profile for the chair TS
Figure 7: IRC reaction animation. (Click to open link; then click on picture to animate)

The result of this IRC calculation was a product structure with an energy of -231.68863 Eh. It is clear that from the end of this job, a local minimum was not reached, due to the RMS gradient being numerically higher than zero. A few alternatives were mentioned, as a solution to this problem:

(i) Run an optimisation on the last point on the IRC obtained - This method was used due to it being the fastest, and also due to the fact that the energy of the structure represented by this point is sufficiently close to the energies obtained for the ten hexadiene conformers (seen above in Table 1)

(ii) Re-run the IRC with more points plotted - This method, if attempted, would not give a different result. This is due to all the other parameters being exactly the same, which would still result in the job terminating prematurely before the other points were plotted. Thus, this method was not used.

(iii) Re-run the IRC specifying the computation of force constants at every step - This method was not attempted, in order to save time and resources.

Optimisation (HF/3-21G)[25] of the last point on the IRC yielded the C2-symmetric Gauche(2) conformer of 1,3-hexadiene (energy = -231.69167 Eh, c.f. Table 1).

From Boat TS to Product

The same IRC calculations specified earlier were run on the HF/3-21G optimised boat TS. The results[26] are as follows:

Figure 7: IRC profile for the chair TS
Figure 8: IRC reaction animation. (Click to open link; then click on picture to animate)

The energy of the system at the last point (-231.67507 Eh) was deemed to be close enough to a local minimum, and an optimisation similar to that detailed in the previous section was run on it[27]. The final product energy was -231.69266 Eh, both energy and geometry matched that of the C1-symmetric Gauche(3) 1,3-hexadiene conformer (c.f. Table 1).

Activation Energies (HF/3-21G & DFT/B3LYP/6-31G*)

In order to compare the effectiveness of both levels of theory at determining the activation energies, both the HF/3-21G optimised TSes (chair and boat) were subjected to a TS(Berny) optimisation[28],[29]. The energies obtained for each TS at these levels of theory were then compared with the lowest energy conformers obtained (Gauche(3) for HF/3-21G; Anti(1) for B3LYP/6-31G*, c.f. Table 1 & 2). The results are detailed in the following table:

Table 6 - Activation Energies for HF/3-21G & DFT/B3LYP/6-31G*
HF/3-21G DFT/B3LYP/6-31G* Literature Activation Energy (kcal/mol)
Transition State Gauche(3) Energy (Eh) TS Energy (Eh) Activation Energy (Eh) Activation Energy (kcal mol-1) Anti(1) (Eh) TS Energy (Eh) Activation Energy (Eh) Activation Energy (kcal mol-1)[30]
Chair -231.69266 -231.61932 0.07334 46.0 -234.61179 -234.55698 0.05481 34.4 33.5 (±0.5)
Boat -231.69266 -231.60280 0.08986 56.4 -234.61179 -234.54309 0.0687 43.1 44.7 (±2.0)

It can be seen from the results that the DFT/B3LYP/6-31G* level of theory gives better agreement with the literature values than HF/3-21G. The influence of the basis set can be seen here, as despite the use of the more comprehensive HF method, the smaller 3-21G basis set possesses limitations in terms of higher error.

Thus, given its lower activation energy, it can be seen that the chair TS is formed more quickly during the Cope Rearrangement, and leads to the "kinetic product", the Gauche(2) conformer.

Suggestions for Improvement: Cope Rearrangement

In order to closely reproduce the literature activation energies, further B3LYP optimisations could be run for each of the conformers (Anti(1) to (4); Gauche(1) to (6)), and an average of all the conformational energies could be obtained. This would then give a more accurate activation energy value.

A further experiment which could be carried out to obtain a more comprehensive IRC would be to use the B3LYP/6-31G* level of theory. Despite requiring more computational resources, the more extensive calculations employed by this theory level would most possibly result in an IRC that ends in a minimised structure.


Diels-Alder Cycloaddition

The Diels-Alder (DA) reaction, as previously seen in Module 1[31], is a pericyclic [4+2] cycloaddition involving a conjugated diene and an olefin (usually termed a "dienophile"). This section will focus on the transition states (TS) of two Diels-Alder cycloadditions, particularly that of cis-butadiene and ethylene, where the concerted, or synchrous, nature of the cycloaddition will be confirmed; and that between maleic anhydride (MA) and cyclohexa-1,3-diene (CH), where the specific regioselectivity (leading to the endo-adduct) of the reaction will be explored. The 6-31G* basis set was used for all the calculations involved from this point.

Diels-Alder Cycloaddition: cis-Butadiene and Ethylene

Synchrous Cycloaddition: Geometry Analysis

The typical curly arrow mechanism for the Diels-Alder cycloaddition always depicts the concerted "pushing" of 6 π-electrons (see Figure 9). The concerted nature of this mechanism can be confirmed via observation of the bond breaking (involving the three π-bonds in the diene and dienophile) and bond forming (of the two σ-bonds and one π-bond in the adduct). The semi-empirical AM1 method was used for the optimisation of both reactants, as well as the TS formed between them (see Jmol files, below). The TS was optimised using an initial "guess" structure involving both reactants aligned such that they resembled the boat structure in a bicyclo-compound, with the distance between the terminal (bond-forming) C atoms set at about 2.2Å.

Figure 9: Mechanism for Diels-Alder reaction between butadiene and ethylene.

[32]

[33]

[34]


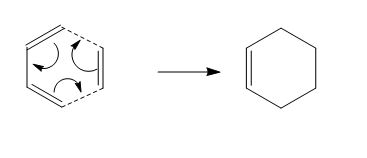
By comparison of the C-C distances (see annotated Jmol files), as well as consideration of typical C-C bond distances[35](ca. 1.53Å, sp3; 1.48Å, sp2 single bond; 1.32Å, sp2 double bond), it can be seen that the reactant geometries are in good agreement with the typical bond lengths, even when considering partial π-electron delocalisation in cis-butadiene. The TS geometry, with respect to the reactants, provides evidence of the following events:

i) Partial formation of two C-C σ-bonds, at the same distance of 2.12Å. Given that the van der Waals' radius[36] of a carbon atom is 1.70Å, it can be seen that this observed C-C distance is less than twice the van der Waals' radius, and that a bond has partially been formed due to attractive overlap of electron density between the two C atoms. The fact that these two C-C distances are alike in the TS suggest that the bonds are formed at the same time.

ii) Lengthening of the sp2 C=C distances from 1.33Å (ethylene) and 1.34Å (cis-butadiene) to 1.38Å, which implies that the C=C bonds have been weakened simultaneously as well.

iii) Shortening of the sp2 C-C single bond in the cis-butadiene fragment from 1.45Å to 1.40Å, showing the partial formation of a double bond.

These geometry changes present in the TS suggest that reaction occurs in one step, and this will be further confirmed by vibrational analysis.

Synchrous Cycloaddition: Analysis of Vibrational Frequencies

Frequency analysis of the TS, as made possible by (opt+freq) calculations, shows that the TS possesses one imaginary stretching frequency at -956 cm-1. The animations for this imaginary vibrational mode and the lowest energy mode are shown in Table 7.

Table 7 - Imaginary and lowest vibrational frequencies of butadiene-ethylene Diels-Alder TS (AM1)[34]
Vib. Frequency (cm-1) Animation
-956 (imaginary)
147

The negative value for the imaginary frequency is attributed to the second derivative of the energy (specifically from the potential energy surface) with respect to the reaction coordinate being negative. This is in turn due to the uphill curvature on which the stationary point corresponding to the TS is found, an energy maximum. The animation for this vibrational frequency corresponds to the reaction coordinate for concerted (or synchrous) bond forming and breaking, and all three events described in the previous section can be observed. Conversely, the lowest stretching frequency, which depicts an asynchrous bond forming/breaking event, does not correspond to a transition state, as its frequency is positive, and corresponds to movement along the potential energy surface minimum.

Symmetry Requirements

Pericyclic reactions are governed by rules of orbital symmetry, and this can be seen especially for this particular DA reaction, whereby both the reactants and TS possess a mirror plane of symmetry. The MOs for the reactant molecules and the TS were calculated using the AM1 method, and used to construct an orbital correlation diagram, as seen in Figures 9 & 10 below.

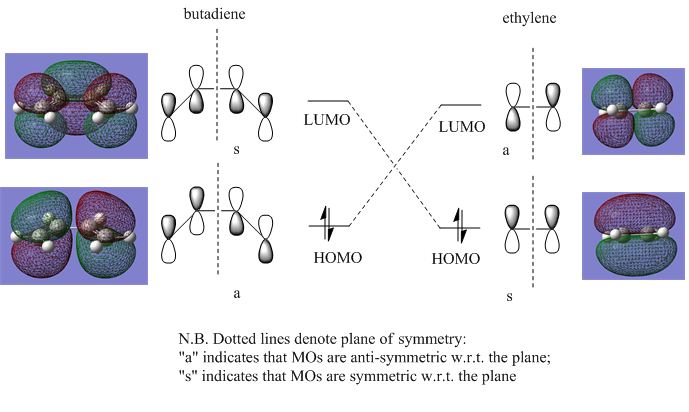
Figure 10: Orbital correlation diagram for butadiene [37] and ethylene[38].

One of the rules that must be observed for an "allowed" DA reaction is that only orbitals of the same symmetry may cross[39], in the correlation diagram. The orbitals are defined as "symmetric" (s) or "anti-symmetric" (a) with respect to a mirror plane of symmetry. As shown by Figure 9, the orbital correlation diagram for the HOMOs and LUMOs of cis-butadiene and ethylene adhere to this orbital crossing rule, and this reaction is formally "allowed". The HOMO and LUMO for the TS are the result of overlap of these symmetry-matched orbitals, and are depicted in Figure 11.

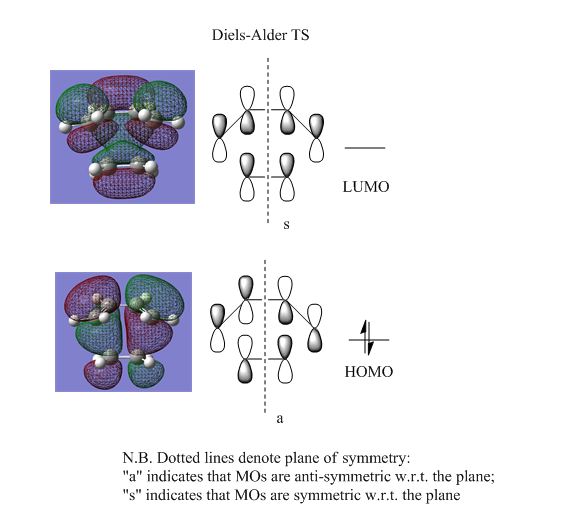
Figure 11: Orbital symmetries for butadiene-ethylene Diels-Alder TS[40].

The HOMO for the transition structure in Figure 11 is anti-symmetric (a) with respect to the plane of symmetry, and is the result of the overlap between the cis-butadiene HOMO and the ethylene LUMO (both of which are anti-symmetric as well, c.f. Figure 10). From this it can be concluded that it is electron donation from the HOMO of the diene to the LUMO of the dienophile that results in the DA reaction.

Diels-Alder Cycloaddition: Cyclohexa-1,3-diene and Maleic Anhydride

The DA reaction between cyclo-1,3-hexadiene (CH) and maleic anhydride (MA) was explored in order to further understand its endo-regioselectivity. Figure 12 depicts two possible orientations of diene and dienophile, which lead to endo- and exo- adducts.

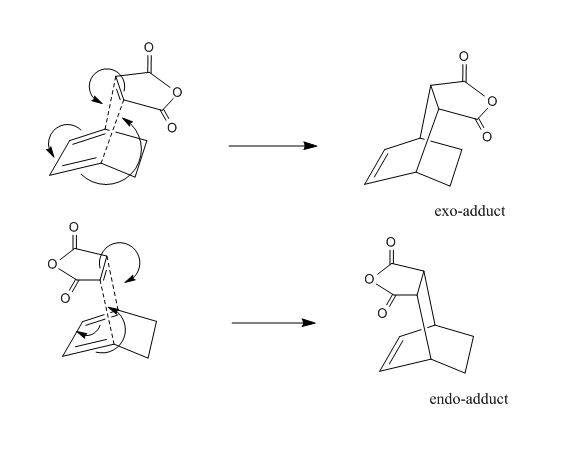
Figure 12: Mechanism for Diels-Alder reaction between cyclohexa-1,3-diene and maleic anhydride.

Relative Energies of the Transition States

AM1 optimisation, frequency and MO calculations were run on both TSes, with the "guess" method (similar orientation as in the previous case) being used to locate the TS geometry in the optimisation calculations.

[41]

[42]


Analysis of the geometries of these TSes (see annotated Jmol files) shows that the two C-C σ-bond formation distances are lower in the endo-TS than in the exo-TS, and this is most probably due to steric crowding in the exo-TS (particularly with respect to the clash between the sp3 bonded H atoms and the anhydride functionality), which limits the approach of the C atoms involved in bonding, towards each other. The relevant energy and frequency results from this AM1 (opt+freq) calculation are shown in Table 8.

Table 8 - Optimisation energies and frequencies of endo-[41] and exo-[42] (MA-CH) Diels-Alder TSes (AM1)
TS Energy (Eh) Relative Energy (kcal mol-1) Vib. Frequency (cm-1) Animation
Endo-TS -0.05150 0.00 -806 (imaginary)
Exo-TS -0.05042 +0.68 -812 (imaginary)


As with the other DA reaction, imaginary vibrational frequencies were obtained, which correspond to the synchrous bond formation which is characteristic of this type of reaction. The AM1 method shows that the exo-TS is indeed higher in energy, by 0.68 kcal mol-1. As mentioned above, implied by the optimised geometries, steric crowding of the exo-TS is a reason for its destabilisation. Another possible reason for the difference in energy between both TSes is the secondary orbital overlap, which will be explored in more detail over the remainder of the wiki.

Secondary Orbital Overlap Effect

The molecular orbitals of the TS were modelled using the AM1 method. As shown in Table 9, while both endo- and exo- HOMOs resemble the antisymmetric TS HOMO found previously in Figure 11 (for cis-butadiene and ethylene), the LUMO+1 level of the endo- TS shows a direct spatial overlap of the MA carbonyl π*-orbitals with the partially formed CH double bond π-orbitals. The exo-TS possesses a nodal plane between the MA carbonyl π*-orbitals and the partially formed CH double bond π-orbitals, and does not benefit from this overlap.

Table 9 - Molecular orbitals of endo-[43] and exo-[44] (MA-CH) Diels-Alder TSes (AM1)
Molecular Orbitals endo-TS exo-TS
LUMO+1
HOMO

A further NBO analysis of these two TSes was not possible due to the Gaussian job crashing whenever the same AM1 job file with the keywords "pop=(full,nbo)" were submitted. It is suspected that the semi-empirical AM1 method does not possess the required parameters for a transition state NBO analysis. Due to this limitation, a separate investigation of the optimised geometries was conducted using the more comprehensive, ab initio MP2 method, which will be detailed in the next section.

MP2 Calculations

The same calculations, with the addition of full NBO analysis, were carried out using the MP2 method and the same 6-31G* basis set. The results are as follows:

Optimisation and Frequency

The optimised TS geometries (obtained via an initial "guess" structure; see also the annotated Jmol files) follow the same trend between the exo- and endo- geometries mentioned earlier; the exo-TS suffers from slightly more steric crowding, and has longer C-C partial bond distances.

[45]

[46]

Both optimised TSes also show a single imaginary vibrational frequency that corresponds to the forward reaction pathway. As also can be seen in Table 10, the difference between endo- and exo-TSes is much more pronounced (about 5 times as high as shown previously for the AM1 optimisation). This further emphasises that the AM1 method is not well suited for the optimisation of transition states, due to the inaccuracy of some of the parameters used. It is also suspected that the MP2 method's higher degree of accuracy in modelling π-electron behaviour makes it more reliable for Hückel-aromatic transition states such as those produced by the Diels-Alder reaction.


Table 10 - Optimisation energies and frequencies of endo-[45] and exo-[46] (MA-CH) Diels-Alder TSes (MP2)
TS Energy (Eh) Relative Energy (kcal mol-1) Vib. Frequency (cm-1) Animation
Endo-TS -610.83622 0.00 -332 (imaginary)
Exo-TS -610.83087 +3.35 -347 (imaginary)
MO and NBO analysis

The MOs of the TSes obtained by the MP2 MO calculations are identical to those obtained by the AM1 method in terms of symmetry, with minor differences. The LUMO+1 levels in this case show that it is possible to reproduce the secondary orbital overlap effect as seen previously.

Table 11 - Molecular orbitals of endo-[47] and exo-[48] (MA-CH) Diels-Alder TSes (MP2)
Molecular Orbitals endo-TS exo-TS
LUMO+1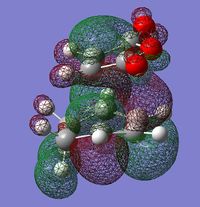
HOMO

The log file which possesses the NBO data shows an electron donation from the partially formed double bond betweeb C5 and C6 into the C15 and C18 (anhydride carbonyl carbon atoms), which is present only for the endo-TS (see log file excerpt below).

Excerpt from endo-TS MO LOG file[47]: 

                                                                              E(2)  E(j)-E(i) F(i,j)
         Donor NBO (i)                     Acceptor NBO (j)                 kcal/mol   a.u.    a.u.
 ===================================================================================================

 from unit  1 to unit  2

  14. BD (   1) C   5 - C   6        /120. RY*(   5) C  15                    0.08    2.75    0.013
  14. BD (   1) C   5 - C   6        /121. RY*(   6) C  15                    0.06    2.30    0.011
  14. BD (   1) C   5 - C   6        /150. RY*(   5) C  18                    0.08    2.75    0.013
  14. BD (   1) C   5 - C   6        /151. RY*(   6) C  18                    0.06    2.30    0.011

However, the magnitude of this interaction is insignificant as it is less than 0.1 kcal mol-1. Therefore it can be concluded that the difference in energy levels between the endo- and exo- TSes is mostly due to steric effects, with little or no contribution from the secondary orbital overlap effect.

Further Discussion

The limitations of the AM1 method as compared to the full ab initio method were highlighted in this section, particularly with regard to transition state calculations. It is proposed, for further work where steric effects must be considered, semi empirical methods should not be assumed to be completely accurate - use of an intermediate approach such as DFT will prove more reliable. However, the AM1 method is useful for smaller, simpler systems, and this is demonstrated by its use in confirming the synchrous nature of the Diels-Alder reaction.

Suggestions for Improvement: Diels-Alder Cycloaddition

More computational experiments could be run to explore normal and inverse electron demands of the [4+2]-cycloaddition. The normal electron demand scenario (already partly investigated in the case of cis-butadiene and ethylene), could be modified by adding electron-withdrawing groups to the dienophile fragment (such as CF3CO2- groups). The inverse electron demand could be investigated by making the diene more electron-withdrawing, via the same modification. The effects of these on transition state energies, if studied, would prove insightful in determining reactivities of these systems.

However, the drawback of this would be the increased computational cost of dealing with systems with more atoms.


Conclusion

The computational methods used here were adept at reproducing the general trends between experimentally observed major kinetic reaction products and lower transition state energies. Investigation of the secondary orbital overlap effect did not prove conclusive, and in general, more extensive computational methods should be used in order to study these phenomena in greater detail.

References

  1. ↑ A. C. Cope, E. M. Hardy, J. Am. Chem. Soc. 1940, 62, 441 - 444 DOI:10.1021/ja01859a055
  2. ↑ https://wiki.ch.ic.ac.uk/wiki/images/4/4f/EW109_REACT_ANTI_1.LOG
  3. ↑ https://wiki.ch.ic.ac.uk/wiki/images/9/98/EW109_REACT_ANTI_2.LOG
  4. ↑ https://wiki.ch.ic.ac.uk/wiki/images/c/c2/EW109_REACT_ANTI_3.LOG
  5. ↑ https://wiki.ch.ic.ac.uk/wiki/images/e/ee/EW109_REACT_ANTI_4.LOG
  6. ↑ https://wiki.ch.ic.ac.uk/wiki/images/f/fd/EW109_REACT_GAUCHE_1.LOG
  7. ↑ https://wiki.ch.ic.ac.uk/wiki/images/5/54/EW109_REACT_GAUCHE_2.LOG
  8. ↑ https://wiki.ch.ic.ac.uk/wiki/images/8/80/EW109_REACT_GAUCHE_3.LOG
  9. ↑ https://wiki.ch.ic.ac.uk/wiki/images/a/ad/EW109_REACT_GAUCHE_4.LOG
  10. ↑ https://wiki.ch.ic.ac.uk/wiki/images/3/34/EW109_REACT_GAUCHE_5.LOG
  11. ↑ https://wiki.ch.ic.ac.uk/wiki/images/7/7c/EW109_REACT_GAUCHE_6.LOG
  12. ↑ http://hdl.handle.net/10042/to-13298
  13. ↑ http://hdl.handle.net/10042/to-13299
  14. ↑ http://hdl.handle.net/10042/to-13300
  15. ↑ 15.0 15.1 http://hdl.handle.net/10042/to-13298
  16. ↑ 16.0 16.1 http://hdl.handle.net/10042/to-13299
  17. ↑ 17.0 17.1 http://hdl.handle.net/10042/to-13300
  18. ↑ http://hdl.handle.net/10042/to-13440
  19. ↑ http://hdl.handle.net/10042/to-13435
  20. ↑ https://wiki.ch.ic.ac.uk/wiki/images/0/0d/EW109_CHAIRTS_OPTREDUNDANT.LOG
  21. ↑ https://wiki.ch.ic.ac.uk/wiki/images/7/70/EW109_CHAIRTS_OPTREDUNDANT2.LOG
  22. ↑ https://wiki.ch.ic.ac.uk/wiki/images/d/d9/EW109_BOATTS_OPTFAIL.LOG
  23. ↑ https://wiki.ch.ic.ac.uk/wiki/images/a/a9/EW109_BOATTS_OPT_QST2_SUCCESS.LOG
  24. ↑ https://wiki.ch.ic.ac.uk/wiki/images/c/cd/EW109_CHAIRTS_IRC.LOG
  25. ↑ https://wiki.ch.ic.ac.uk/wiki/images/e/e8/EW109_CHAIRTS_POSTIRC_OPT.LOG
  26. ↑ https://wiki.ch.ic.ac.uk/wiki/images/2/2d/EW109_BOATTS_IRC.LOG
  27. ↑ https://wiki.ch.ic.ac.uk/wiki/images/3/3f/EW109_BOATTS_POSTIRC_OPT.LOG
  28. ↑ http://hdl.handle.net/10042/to-13478
  29. ↑ http://hdl.handle.net/10042/to-13479
  30. ↑ https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3#Optimizing_the_.22Chair.22_and_.22Boat.22_Transition_Structures
  31. ↑ https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:TheWongAndWindingRoad#Diels-Alder_Dimerisation_of_Cyclopentadiene
  32. ↑ http://hdl.handle.net/10042/to-13566
  33. ↑ http://hdl.handle.net/10042/to-13567
  34. ↑ 34.0 34.1 http://hdl.handle.net/10042/to-13569
  35. ↑ M. Smith, J. March, March's Advanced Organic Chemistry: Reactions, Mechanisms, and Structure, 2007
  36. ↑ A. Bondi, J. Phys. Chem., 1964, 68, 441–451 DOI:10.1021/j100785a001
  37. ↑ http://hdl.handle.net/10042/to-13571
  38. ↑ https://wiki.ch.ic.ac.uk/wiki/images/3/3e/EW109_ETHY_AM1_MOS.LOG
  39. ↑ http://www.ch.ic.ac.uk/local/organic/pericyclic/p1_theory.html
  40. ↑ https://wiki.ch.ic.ac.uk/wiki/images/a/a9/EW109_BUTA_ETHY_TS_MOS_AM1.LOG
  41. ↑ 41.0 41.1 https://wiki.ch.ic.ac.uk/wiki/images/9/94/EW109_MALEI_CYCLO_ENDO_AM1_OPT.LOG
  42. ↑ 42.0 42.1 http://hdl.handle.net/10042/to-13574
  43. ↑ http://hdl.handle.net/10042/to-13575
  44. ↑ http://hdl.handle.net/10042/to-13573
  45. ↑ 45.0 45.1 http://hdl.handle.net/10042/to-13576
  46. ↑ 46.0 46.1 http://hdl.handle.net/10042/to-13577
  47. ↑ 47.0 47.1 http://hdl.handle.net/10042/to-13578
  48. ↑ http://hdl.handle.net/10042/to-13579
Retrieved from "https://chemwiki.ch.ic.ac.uk/index.php?title=Rep:Mod:WhatWentWong&oldid=818208"