Rep:Mod:Weathercock

Cope rearrangement tutorial

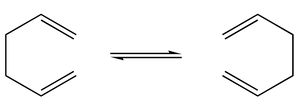
In this part, Cope rearrangement of 1,5-hexadiene (shown on the right) is studied using computational methods.

Cope rearrangement of 1,5-hexadiene.

Optimization of starting material and product

Both starting material and product of the reaction is 1,5-hexadiene. Four conformations of this diene were optimized using two methods:

a) Hartree-Fock with 3-21G basis set

b) B3LYP DFT with 6-31(d) basis set, using the structure optimized with method a) as an input

The results are shown in the table below:

			Hartree-Fock, 3-21G	B3LYP, 6-31G(d)
conformer	image of B3LYP-optimized structure	point group	electronic energy [Hartree]	electronic energy [Hartree]	rel. energy [Hartree]	rel. energy [kcal/mol]
anti 1 input file output file (HF) output file (B3LYP)		C2	-231.69260235	-234.61180037	0.00000000	0.00
anti 2 input file output file (HF) output file (B3LYP)		Ci	-231.69253518	-234.61170273	0.00009764	0.06
gauche 2 input file output file (HF) output file (B3LYP)		C2	-231.69166702	-234.61070764	0.00109273	0.69
gauche 3 input file output file (HF) output file (B3LYP)		C1	-231.69266122	-234.61132934	0.00047103	0.30

As seen in the output files, the geometry of each molecule stayed the same after the second optimization, with bond lengths differing by 0.01-0.02 Å.

Trivially, the energy values of conformers calculated with different methods are different. However, the ordering of these energies also changed. As expected, the conformers with antiperiplanar ("anti") geometry around the central two carbon atoms have lower energies than gauche conformers after using the more accurate B3LYP computation. Just like in alkanes, three factors are expected to influence the relative energies of conformers:

a) orbital overlap (σ_C-H/σ*_C-H, σ_C-C/σ*_C-H, σ*_C-C/σ_C-H)

b) bond-bond repulsion (Pauli repulsion)

c) Van der Waals attractive interactions

In n-butane, effect a) lowers the energy of antiperiplanar conformation while b) and c) approximately cancel each other, hence the lowest energy conformer of this molecule is antiperiplanar. For 1,5-hexadiene the the values of these contributions are expected to be different, because:

a) the σ_C-C. and σ*_C-C orbitals are formed from one sp² and one sp³ orbitals

b) bond-bond repulsion energy is different because the overall shape of the molecule is different

c) in gauche conformations, two alkene groups are closer, which are suspected to attract by Van der Waals interactions

However, the lowest energy conformation is still antiperiplanar.

In all four conformers, the conformation of the alkene group is such that the hydrogen in the -CH= fragment is in gauche position. This is called A^1,3-eclipsed conformation and is known to be the lowest energy conformation of alkenes. The energy is lowered due to the overlap with π orbital, in this case π_C=C/σ*_C-H, π*_C=C/σ_C-H, π_C=C/σ*_C-C, π*_C=C/σ_C-C.

The energy difference between the two antiperiplanar conformations is small and we can't exactly say where does it come from unless more detailed computational studies are performed.

The optimized anti 1 and anti 2 conformers were then used for frequency computations using the same methods as for optimization. Output files:

Hartree-Fock:

anti 1: https://wiki.ch.ic.ac.uk/wiki/images/b/b9/SB_ANTIPP1_FREQ.LOG

anti 2: https://wiki.ch.ic.ac.uk/wiki/images/a/a6/SB_ANTIPP2_FREQ.LOG

B3LYP:

anti 1: https://wiki.ch.ic.ac.uk/wiki/images/0/06/SB_ANTIPP1_2_FREQ.LOG

anti 2: https://wiki.ch.ic.ac.uk/wiki/images/8/88/SB_ANTIPP2_2_FREQ.LOG

All the computed frequencies are positive, confirming that the structures reached the energy minimum.

Optimizing the transition states

The Cope rearrangement can proceed via two transition states:

Chair transition state	Boat transition state

where the chair transition state has slightly lower energy. In the following section, the Hartree-Fock method with 3-21G basis set was used to optimize the transition state structures and perform the IRC computation.

Chair transition state

Chair transition state was optimized using two methods.

Direct computation using the guess structure

As an input, a guess structure was set up from two neutral allyl fragments (CH₂CHCH₂) placed on top of each other, with distance ca. 2.20 Å between terminal carbon atoms. Input file: https://wiki.ch.ic.ac.uk/wiki/images/7/79/SB_TS_chair_guess.gjf

The structure was then optimized using Berny method. Output file:

https://wiki.ch.ic.ac.uk/wiki/images/0/05/SB_TS_CHAIR_1.LOG

The resultant structure:

The distances between the terminal carbon atoms are now 2.02023 Å and 2.02048 Å. The computed frequencies confirm that a transition state structure was reached - one of the frequencies is negative (-818 cm^-1). This vibration mode having this frequency indeed corresponds to Cope rearrangement:

Computation using a restricted coordinate

The same guess structure was used for an optimization using a "frozen coordinate" - the distances between the terminal carbons were fixed and the structure was optimized to energy minimum. Output file:

https://wiki.ch.ic.ac.uk/wiki/images/1/15/SB_TS_CHAIR2.LOG

The output structure was then optimized to a transition state (Berny method). Output file:

https://wiki.ch.ic.ac.uk/wiki/images/e/e2/SB_TS_CHAIR3.LOG

The resultant structure looks very similar to previous one:

The terminal carbon distances are very similar to the ones obtained previously: 2.02054 and 2.02016 Å.

Boat transition state

The structure of the boat transition state was optimized with QST2 method, using "bent" structure of the anti-2 conformer as the starting material and product:

Reactant	Product

Input file:

https://wiki.ch.ic.ac.uk/wiki/images/9/96/SB_TS_boat_2.gjf

Output file:

https://wiki.ch.ic.ac.uk/wiki/images/b/b9/SB_TS_BOAT_2.LOG

Resultant structure:

The terminal carbon distances are now 2.13999 and 2.14002 Å. As in case of the chair transition state, the vibrational analysis shows one negative frequency (-840 cm^-1) originating from the mode corresponding to the Cope rearrangement.

IRC computation

In order to check what kind of conformer is obtained directly from the chair transition state, IRC (intrinsic reaction coordinate) computation was set up. The chair structure optimized directly from the guess structure was used. The number of steps was set to 50. Input file:

https://wiki.ch.ic.ac.uk/wiki/images/1/10/SB_CHAIR_1_IRC_1.gjf

Output file:

https://wiki.ch.ic.ac.uk/wiki/images/1/1e/SB_CHAIR_1_IRC_1.LOG

The transition state turned in 44 steps into a structure resembling the gauche 2 conformation of 1,5-hexadiene:

The obtained structure was then optimized to energy minimum. The result didn't differ much. Output file:

https://wiki.ch.ic.ac.uk/wiki/images/2/23/SB_CHAIR_1_IRC_2.LOG

The conformation obtained directly from the transition state is not the lowest energy one (anti 1). When we inspect all the computed transient structures (output file), we see that the two halves of the diene molecule "open up" without any rotation around bonds, which results in gauche 2 product conformation. In order to obtain the anti 1 or 2 conformation, the molecule has to additionally rotate around the central C-C bond, which requires to overcome a potential barrier.

Activation energy calculation

The transition state structures optimized by the Hartree-Fock method were optimized further using the B3LYP method with 6-31G(d) basis set, together with frequency calculations. The chair transition state optimized from the guess structure was used. Output files:

chair TS: https://wiki.ch.ic.ac.uk/wiki/images/5/57/SB_TS_CHAIR_1_2.LOG

boat TS: https://wiki.ch.ic.ac.uk/wiki/images/d/d8/SB_TS_BOAT_2_2.LOG

The geometries of the transition states are similar, with the terminal bond distances differing by ca. 3% (in chair TS, the lengths decreased from 2.020 to 1.968 Å, in boat TS, the lengths increased from 2.140 to 2.207 Å.). However, the calculated frequencies are significantly different - the negative frequency of the vibration mode corresponding to the reaction is now -566 cm^-1 (chair TS) and -530 cm^-1 (boat TS). This is because the force constants (calculated as second derivatives of the energy with respect to displacement) were calculated by the new method to have different values.

In the table below, the energies of the transition states, including energies with vibrational contributions are shown. All energies are given in Hartrees.

	Hartree-Fock, 3-21G			B3LYP, 6-31G(d)
	electronic energy	sum of electronic and zero-point energies (0 K)	sum of electronic and thermal energies (298.15 K)	electronic energy	sum of electronic and zero-point energies (0 K)	sum of electronic and thermal energies (298.15 K)
chair TS	-231.61932239	-231.466699	-231.461340	-234.55698303	-234.414929	-234.409009
boat TS	-231.60280249	-231.450929	-231.445300	-234.54309307	-234.402342	-234.396008
anti 1	-231.69260235	-231.539601	-231.532644	-234.61180037	-234.469286	-234.461965

Knowing the energies of both the starting material and the transition state, it is possible to calculate the activation energy of the reaction. The activation energies, calculated as the difference between energies of transition state and the diene in anti 1 conformation (lowest energy conformation), are shown below. The energies with vibrational contributions were used. All energies are given in kcal/mol.

	HF, 3-21G (0 K)	HF, 3-21G (298.15 K)	B3LYP, 6-31G(d) (0 K)	B3LYP, 6-31G(d) (298.15 K)	experimental (0 K)
AE (chair TS)	45.75	44.74	34.11	33.23	33.5 ± 0.5
AE (boat TS)	55.64	54.81	42.01	41.39	44.7 ± 2.0

As can be seen, the activation energies calculated from with the B3LYP method are significantly lower and very close to the experimental energies, which justifies optimizing the structures with this method and basis set.

The Diels-Alder cycloadditon

Butadiene + ethene cycloaddition

The simplest example of the Diels-Alder reaction is the addition of ethene to butadiene (shown on the right).

Diels-Alder cycloaddition of butadiene and ethene.

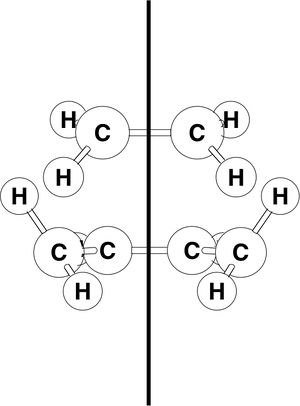
In this section, the molecular orbitals involved in the reaction are explored. The symmetry labels applied to the orbitals denote their symmetry with respect to the plane of symmetry perpendicular to the planes of both molecules (shown on the right). "Symmetric" molecular orbital has planar symmetry while "antisymmetric" orbital retains shape after the reflection but has opposite signs of wavefunction.

Plane of symmetry for symmetry labels.

For the following computations, the AM1 semi-empirical method was used.

Starting materials

Ethene molecule was optimized and molecular orbitals were plotted. Output files:

https://wiki.ch.ic.ac.uk/wiki/images/f/f6/SB_ETHENE.LOG

https://wiki.ch.ic.ac.uk/wiki/images/3/32/SB_ethene.chk

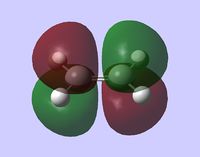
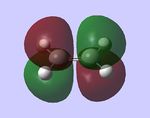
As expected, the HOMO of ethene is the π bonding orbital (symmetric):

and the LUMO is the π* antibonding orbital (antisymmetric):

In the same way, butadiene molecule was optimized. Output files:

https://wiki.ch.ic.ac.uk/wiki/images/7/72/SB_BUTADIENE.LOG

https://wiki.ch.ic.ac.uk/wiki/images/c/c2/SB_butadiene.chk

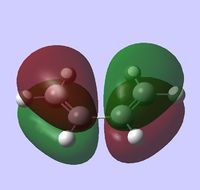
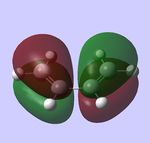
HOMO is antisymmetric:

LUMO is symmetric:

Transition state

In order to optimize the transition state, a guess structure was set up, consisting of cyclohexene ring with a -CH₂CH₂- fragment (C-C bond length: 1.23 Å) bent out of plane at an angle of ca. 59°. The bonds between the -CH₂CH₂- fragment were set to 2.15 Å. Input file:

https://wiki.ch.ic.ac.uk/wiki/images/2/2f/SB_DA_1_TS_guess.gjf

The guess structure was then optimized to a transition state (Berny method), together with frequency computations. Output files:

https://wiki.ch.ic.ac.uk/wiki/images/9/9b/SB_DA_1_TS_guess.chk

https://wiki.ch.ic.ac.uk/wiki/images/8/80/SB_DA_1_TS_GUESS.LOG

The resultant structure is shown below:

The distances between terminal carbon atoms in the computed transition state are 2.11900 and 2.11936 Å, which is much longer than typical single C-C bonds (1.54 Å for sp³-sp³, 1.47 Å for sp²-sp²)). This is because the bonds in the transition state are being formed and have not yet reached the equilibrium length obtained in the product. On the other hand, the obtained distances are smaller than two van der Waals radii of carbon (1.70 Å), so the bonding interactions between carbon atoms are already significant.

As expected, the vibrational analysis of the transition state shows one mode with negative frequency (-956 cm^-1). This mode corresponds to simultaneous bond formation (or bond breaking) during the reaction:

On the other hand, the lowest positive frequency mode corresponds to twisting of two reactant fragments with respect to each other:

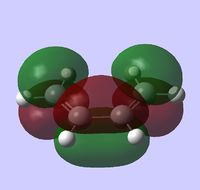
The computed HOMO of the transition state is antisymmetric:

while the LUMO is symmetric:

It's easy to notice that the frontier orbitals of the transition state resemble the overlapping frontier orbitals of both reactants. In the table below, the formation of the transition state orbitals is summarized:

ethene	butadiene	transition state
LUMO, antisymmetic	HOMO, antisymmetric	HOMO, antisymmetric
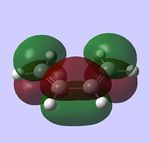HOMO, symmetric	LUMO, symmetric	LUMO, symmetric

The HOMO/LUMO overlap (constructive interference of wavefunctions) is what makes the cycloaddition possible - the two new sigma bonds are formed by diene HOMO donating the electron density to the ethene LUMO (visible as the two large lobes between the molecules in the TS HOMO). At the same time, the ethene HOMO donates (some) electron density to the antibonding π* orbtials in the diene, which corresponds to breaking of double bonds (the C=C bond length is 1.33 Å in butadiene and 1.38 Å in the transition state).

The overlap between the orbitals is associated with having the same symmetry properties - symmetric orbital overlaps with another symmetric orbital and asymmetric orbital overlaps with another asymmetric orbital. If the symmetry properties of the HOMO and LUMO of reactants were different (not leading to overlap), the reaction would not occur. This is the reason why this reaction proceeds with suprafacial geometry (which in this case means almost no rotation of CH₂ groups in diene or ethene).

The cycloaddition between ethene and butadiene is possible, hut occurs in poor yield . This is because in unsubstituted alkene and diene the overlapping HOMO and LUMO orbitals have much different energies. This is why in most Diels-Alder reactions we use electron deficient alkene as dienophile so that its LUMO has lower energy (and therefore closer to the diene's HOMO). Alternaively, one can use dienophle with electron donating groups and a diene with electron withdrawing groups (a situation known as "reverse electron demand").

Cyclohexa-1,3-diene + maleic anhydride cycloaddition

Diels-Alder cycloaddition between cyclohexa-1,3-diene (1) and maleic anhydride (2) gives exo product (3) and endo product (4).

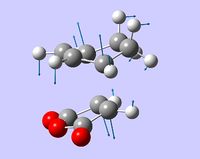
In this section, a Diels-Alder reaction between a cyclohexa-1,3-diene and maleic anhydride (shown on the right) is investigated. The reaction can proceed via two transition states, leading to two different products: endo and exo. Experimental results show that the reaction is under kinetic control, which causes the endo to predominate.

Both transition states were drawn as guess structures and then optimized (together with frequency calculations) by the AM1 semi-empirical method. The output files of these calculations were then used for a more accurate optimization using B3LYP DFT method with 6-31G(d) basis set. This method and basis set already proved to give results in agreement with experimental measurements (see previous sections). In both cases, the transition states were reached, which was confirmed by one negative frequency mode, corresponding to synchronous bond formation (shown in the table below).

	exo-TS	endo-TS
files	input file .log output file (AM1) .chk output file (B3LYP) .log output file (B3LYP)	input file .log output file (AM1) .chk output file (B3LYP) .log output file (B3LYP)
image of B3LYP-optimized structure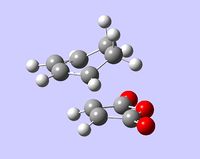
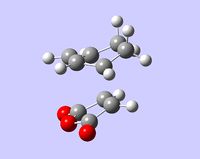
negative frequency vibration mode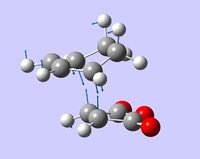
sum of electronic and zero-point energies (0 K) [Hartrees]	-612.498012	-612.502142
length of the formed σ bond [Å]	2.29056, 2.29058	2.26873, 2.26842
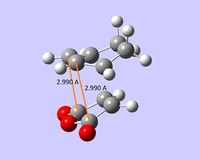
non-covalent distances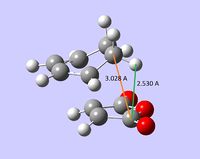
LUMO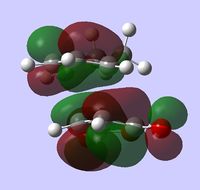
HOMO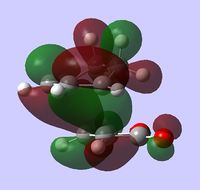
HOMO-1
secondary interactions	(MO 34) 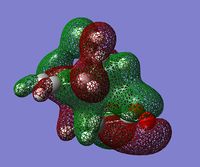(MO 37)	(MO 37)

The computed energy of the endo transition state is lower than that of exo, in agreement with experimental observations. The difference equals ca. 2.6 kcal/mol.

In both transition structures, the distances between the anhydride group and the neighboring hydrocarbon fragment are below the respective sum of van der Waals radii (C: 1.70 Å, H: 1.20 Å), hence there probably exist repulsive (steric) interactions between these fragments. The repulsion is expected to be larger for the exo structure because the anhydride group approaches closely both carbon and hydrogen atoms.

The lower energy of the endo transition state (and therefore the steroselectivity of the reaction) is explained by the secondary orbtial interactions in this transition state, i.e. the interactions between orbitals where they are not involved in making bonds. Such interactions however, are not very apparent in HOMO or HOMO-1 orbitals - there is a correct arrangement of oxygen p orbitals in the endo HOMO for overlap to occur but there is no significant overlap shown in the plot. Some stabilizing interactions can however be seen in the lower energy orbitals: MO 37 of endo transition state or in MO 34 and 37 of exo transition state. Because we can notice these interactions in both transition states, one can't simply predict which structure has lower energy by visual inspection of the MO plots.

Further discussion

Effects neglected in the computations of transition states:

a) Interaction with solvent and/or other molecules. Pericyclic reactions don't proceed via ionic intermediates (by definition), so the effect of solvent on reaction in general is low. In fact, Diels-Alder reactions don't need solvent at all - the reactants can be mixed together. On the other hand, carrying out the reaction by adding reagents to water is known to both accelerate the reaction and increase the endo selectivity.