Rep:Mod:WSL1819
Optimisation of NH3
General Information of Optimised NH3
From the 'Summary' table (Figure 1.1), the following general information about the optimisation calculation is obtained: the molecule optimised is ammonia, NH3, the calculation method is RB3LYP; the basis set is 6-31G(d,p); the final energy E(RB3LYP) is -56.44397188 a.u.; the RMS gradient is 0.05399560 a.u.; and the point group of NH3 is C3v.
Geometric Information of Optimised NH3
Optimised bond length: 1.01798 Å ≈ 1.018 Å
Optimised bond angle: 105.741 o ≈ 105.7 o
Verification of Successful Optimisation of NH3
The 'Item' table (Figure 1.2) shows that the final set of forces and displacements are converged and that the forces are approximately zero; since force is the gradient of a potential energy vs distance graph, this indicates that the structure obtained is at equilibrium, demonstrating successful optimisation of NH3.
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
Figure 1.2: Item Table of optimised NH3
Moreover, successful optimisation of NH3 is indicated by the last structure having the most negative energy and the smallest gradient (Figure 1.3).
Dynamic Image of Optimised NH3
test molecule |
Figure 1.4: A 3D jmol file of optimised NH3
The optimisation file is linked to here
Vibrational Analysis of Optimised NH3
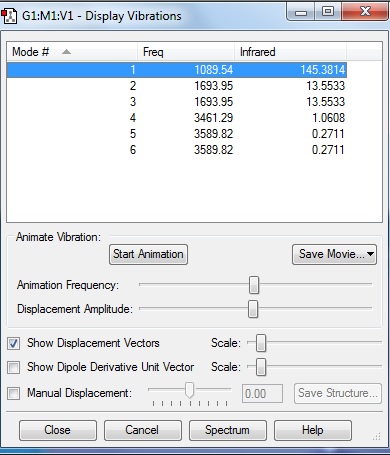
From Figure 1.5 in vibrational analysis, there are 6 modes as expected, modes 2 and 3 and modes 5 and 6 are degenerate as they have the same frequency of 1693.95 cm-1 and 3589.82 cm-1 respectively; modes 1, 2 and 3 are "bending" vibrations and modes 4, 5 and 6 are "bond stretch" vibrations; mode 4 is highly symmetric ; mode 1 is the "umbrella" mode and 2 bands in the experimental spectrum (Figure 1.6) of gaseous ammonia as expected.
2 bands in the experimental spectrum are expected firstly because modes 4, 5 and 6 have very small intensities due to small rate of change of dipole moment and since its an experimental spectrum, the noise is great enough to cover such small intensities and secondly because modes 2 and 3, though with significant intensities, are degenerate.
Charge Analysis of Optimised NH3
Charge analysis (Figure 1.7) shows the charge on the nitrogen atom is -1.125 whilst that of the hydrogen atoms is +0.375. This result where nitrogen has a negative charge with a larger magnitude and hydrogen has a positive charge with a smaller magnitude is expected, since nitrogen is more electronegative than hydrogen, nitrogen should withdraw more electron density from each of the three N-H bonds.
Optimisation of N2
General Information of Optimised N2
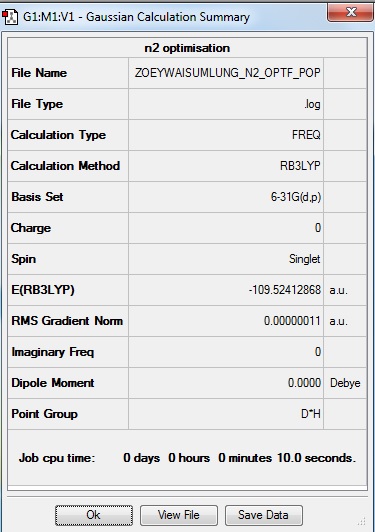
From the 'Summary' table (Figure 2.1), the following general information about the optimisation calculation is obtained: the molecule optimised is nitrogen, N2, the calculation method is RB3LYP; the basis set is 6-31G(d,p); the final energy E(RB3LYP) is -109.52412868 a.u.; the RMS gradient is 0.00000011 a.u.; and the point group of N2 is D∞h.
Geometric Information of Optimised N2
Optimised bond length: 1.10550 Å ≈ 1.106 Å
Verification of Successful Optimisation of N2
The 'Item' table (Figure 2.2) shows that the final set of forces and displacements are converged and that the forces are zero; since force is the gradient of a potential energy vs distance graph, this indicates that the structure obtained is at equilibrium, demonstrating successful optimisation of N2.
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
Figure 2.2: Item Table of optimised N2
Moreover, successful optimisation of N2 is indicated by the last structure having the most negative energy and the smallest gradient (Figure 2.3).
Dynamic Image of Optimised N2
Figure 2.4: Optimised nitrogen |
The optimisation file is linked to here
Vibrational Analysis of Optimised N2
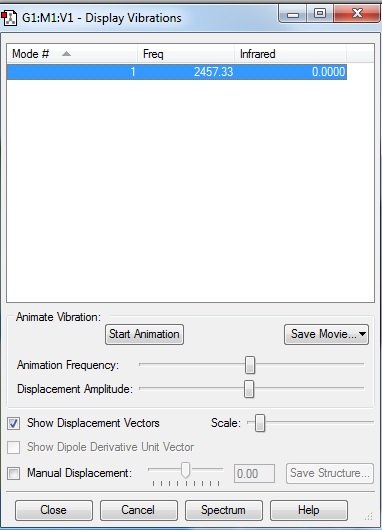
From Figure 2.5 in vibrational analysis, there are 0 modes as expected, and 0 bands in the experimental spectrum (Figure 2.6) of gaseous nitrogen as expected.
No bands are expected to be seen in the experimental spectrum because nitrogen is a linear molecule there is no dipole moment hence no change in dipole moment in a linear molecule.
Charge Analysis of Optimised N2
Charge analysis (Figure 2.7) shows the charge on both nitrogen atoms is 0.000. This result is expected because both atoms of the lienar bond are the same so there are no expected differences in electronegativity therefore electron density is shared equally between the nitrogen atoms. Note that the atoms are colored by charge, a charge of 0.000 is represented by the color black and the numbers are written in black therefore they cannot be seen here.
Optimisation of H2
General Information of Optimised H2
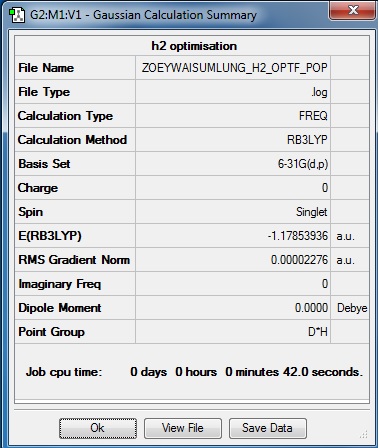
From the 'Summary' table (Figure 3.1), the following general information about the optimisation calculation is obtained: the molecule optimised is hydrogen, H2, the calculation method is RB3LYP; the basis set is 6-31G(d,p); the final energy E(RB3LYP) is -1.17853936 a.u.; the RMS gradient is 0.00002276 a.u.; and the point group of H2 is D∞h.
Geometric Information of Optimised H2
Optimised bond length: 0.74274 Å ≈ 0.7427 Å
Verification of Successful Optimisation of H2
The 'Item' table (Figure 3.2) shows that the final set of forces and displacements are converged and that the forces are zero; since force is the gradient of a potential energy vs distance graph, this indicates that the structure obtained is at equilibrium, demonstrating successful optimisation of H2.
Item Value Threshold Converged? Maximum Force 0.000039 0.000450 YES RMS Force 0.000039 0.000300 YES Maximum Displacement 0.000052 0.001800 YES RMS Displacement 0.000073 0.001200 YES
Figure 3.2: Item Table of optimised H2
Moreover, successful optimisation of H2 is indicated by the last structure having the most negative energy and the smallest gradient (Figure 3.3).
Dynamic Image of Optimised H2
Figure 3.4: Optimised hydrogen |
The optimisation file is linked to here
Vibrational Analysis of Optimised H2
From Figure 3.5 in vibrational analysis, there are 0 modes as expected, and 0 bands in the experimental spectrum (Figure 3.6) of gaseous hydrogen as expected.
No bands are expected to be seen in the experimental spectrum because hydrogen is a linear molecule there is no dipole moment hence no change in dipole moment in a linear molecule.
Charge Analysis of Optimised H2
Charge analysis (Figure 3.7) shows the charge on both hydrogen atoms is 0.000. This result is expected because both atoms of the linear bond are the same so there are no expected differences in electronegativity therefore electron density is shared equally between the hydrogen atoms. If a higher basis set is used, a single bond would likely to be displayed.
Energy Analysis
E(NH3) = -56.44397188 a.u. 2*E(NH3)= -112.88794376 a.u. E(N2)= -109.52412868 a.u. E(H2)= -1.17853936 a.u. 3*E(H2)= -3.53561808 a.u. ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -112.88794376 a.u. - (-109.52412868 a.u. + -3.53561808 a.u.) = -112.88794376 a.u. -(-113.05974676) a.u. = + 0.171803 a.u. = +451.0687765 kJ/mol = +451.07 kJ/mol
However, the forward reaction is supposed to be exothermic, further optimisation would be needed.
Optimisation of S2
General Information of Optimised S2
From the 'Summary' table (Figure 4.1), the following general information about the optimisation calculation is obtained: the molecule optimised is sulphur, S2, the calculation method is RB3LYP; the basis set is 6-31G(d,p); the final energy E(RB3LYP) is -796.32599779 a.u.; the RMS gradient is 0.00000905 a.u.; and the point group of S2 is D∞h.
Geometric Information of Optimised S2
Optimised bond length: 1.92947 Å ≈ 1.929 Å
Verification of Successful Optimisation of S2
The 'Item' table (Figure 4.2) shows that the final set of forces and displacements are converged and that the forces are approximately zero; since force is the gradient of a potential energy vs distance graph, this indicates that the structure obtained is at equilibrium, demonstrating successful optimisation of S2.
Item Value Threshold Converged? Maximum Force 0.000016 0.000450 YES RMS Force 0.000016 0.000300 YES Maximum Displacement 0.000027 0.001800 YES RMS Displacement 0.000038 0.001200 YES
Figure 4.2: Item Table of optimised S2
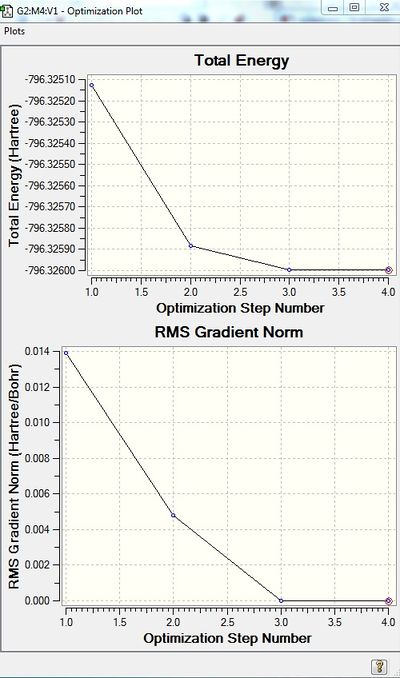
Moreover, successful optimisation of S2 is indicated by the last structure having the most negative energy and the smallest gradient (Figure 4.3).
Dynamic Image of Optimised S2
Figure 4.4: Optimised sulphur |
The optimisation file is linked to here
Vibrational Analysis of Optimised S2
From Figure 4.5 in vibrational analysis, there are 0 modes as expected, and 0 bands in the experimental spectrum (Figure 4.6) of gaseous sulphur as expected.
No bands are expected to be seen in the experimental spectrum because sulphur is a linear molecule there is no dipole moment hence no change in dipole moment in a linear molecule.
Charge Analysis of Optimised S2
Charge analysis (Figure 4.7) shows the charge on both sulphur atoms is 0.000. This result is expected because both atoms of the linear bond are the same so there are no expected differences in electronegativity therefore electron density is shared equally between the sulphur atoms. A single bond instead of a double bond is displayed however this would most likely not be the case if a higher basis set is used for optimisation.
Molecular Orbitals of Optimised S2
| heading | heading |
|---|---|
 |
The two 1s AOs form a non-bonding σ MO. The energy of the MO formed is -88.93663 a.u. The MOs cannot be visualised and there is minimal if no interaction between the orbitals because the AOs are so concentrated within each of the individual respective nuclei and they are so small. |
 |
The two 1s AOs form a non-bonding σ* MO. The energy of the MO formed is -88.93661 a.u. The MOs cannot be visualised and there is minimal if no interaction between the orbitals because the AOs are so concentrated within each of the individual respective nuclei and they are so small. |
 |
The two 2s AOs form a non-bonding σ MO. The energy of the MO formed is -7.99779 a.u. |
 |
The two 2s AOs form a non-bonding σ* MO. The energy of the MO formed is -7.99769 a.u. |
  |
The two 2px and two 2py AOs form two non-bonding π MOs. These two orbitals are degenerate- the energies of the MOs are -5.96349 a.u. and -5.94946 a.u. respectively. |
  |
The two 2px and two 2py AOs form two non-bonding π* MOs. These two orbitals are degenerate- the energies of the MOs are -5.96135 a.u. |
 |
The two 2pz AOs form one non-bonding σ MO. The energy of the MO is -5.96135 a.u. |
 |
The two 2pz AOs form one non-bonding σ * MOs. The energy of the MO is -5.96078 a.u. |
 |
The two 3s AOs overlap constructively head=on to form a bonding σ MO. The energy of the MO formed is -0.83212 a.u. |
 |
The two 3s AOs overlap destructively to form an anti-bonding σ* MO. The energy of the MO formed is -0.61535 a.u. |
 |
The two 3pz AOs overlap constructively head-on to form a bonding σ MO. The energy of this bonding MO is -0.39516 a.u. The energy of this MO is lower in energy than the bonding MOs formed from the overlap of the two 2px and the two 2py orbitals because the head-on interaction is much stronger than the lateral interactions. |
  |
The two 3px and the two 3py AOs overlap constructively laterally to form two bonding π MOs of relatively the same energy of -0.36283 a.u. and -0.34958 a.u. respectively. |
  |
The two 3px and the two 3py AOs overlap destructively laterally to form two anti-bonding π* MOs of relatively the same energy of -0.21843 a.u. and -0.18463 a.u. respectively. It is important to note that these two anti-bonding π* MOs formed are the HOMO and LUMO respectively of sulphur, meaning that all reactions would react with the sulphur-sulphur pi-bond and not the sigma bond of the double bond. |
 |
The two 3pz AOs overlap destructively head-on to form an anti-bonding σ* MO. The energy of this bonding MO is -0.01307 a.u. |