Rep:Mod:WS4718
Part 1: NH3 Molecule
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| E(RB3LYP) | -56.55776873 au |
| RMS Gradient | 0.00000485 au |
| Point Group | C3V |
| N-H Bond Distance | 1.02 ± 0.01 Å |
| H-N-H Bond Angle | 106 ± 1 ° |
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Ammonia Molecule |
The optimisation file is linked to here
Part 2: Vibration and Charge Analysis of NH3 Molecule
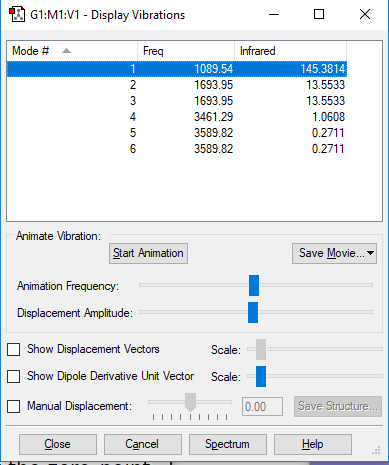
Display Vibrations
| Mode | wavenumber (cm-1) | symmetry | Intensity (au) | Image |
|---|---|---|---|---|
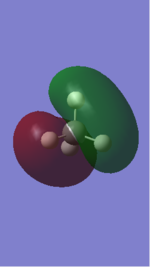
| 1 | 1090 | A1 | 145 | 
|
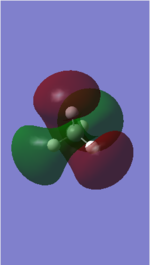
| 2 | 1694 | E | 14 | 
|
| 3 | 1694 | E | 14 | 
|
| 4 | 3461 | A1 | 1 | 
|
| 5 | 3590 | E | 0.3 | 
|
| 6 | 3590 | E | 0.3 | 
|
• You would expect from the 3N-6 rule that there would be 6 vibration modes, where in NH3 N=4
• Modes 2 and 3 are degenerate (at 1694 cm-1) , as well as modes 5 and 6 (at 3590 cm-1). They are the same energy, as shown by identical frequency, intensity and symmetry data
• Modes 1 (at 1090 cm-1), 2 (at 1694 cm-1) and 3 at 1694 cm-1) are 'bending' vibrations and modes 4 (at 3461 cm-1) , 5 (at 3590 cm-1) and 6 (at 3590 cm-1) are 'stretching' vibrations
• Mode 4 (at 3461 cm-1) is highly symmetric
• Mode 1 (at 1090 cm-1) is known as the 'umbrella' mode
• You would expect to see 2 bands on an experimental spectrum of gaseous ammonia, this is because the intensity of modes 4 and (5/6) is so low it would not be visible on the spectra. Moreover, 2/3 are degenerate.
Charge Analysis
• The nitrogen atom is negatively charged as it is more electronegative, hence more electron withdrawing than the hydrogen atoms. Leaving the hydrogen atoms with a corresponding positive charge as the negatively charged bonding electrons are 'pulled' closer to the nitrogen atom. As such the nature of the bond isn't purely covalent and has ionic character.
Part 3: Reaction Energy and Molecular Orbitals for Hydrogen and Nitrogen
Hydrogen
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| E(RB3LYP) | -1.17853930 au |
| RMS Gradient | 0.00000017 au |
| Point Group | D*H |
| H-H Bond Distance | 0.074 ± 0.01 Å |
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES Predicted change in Energy=-1.164080D-13 Optimization completed.
Hydrogen Molecule |
The optimisation file is linked to here
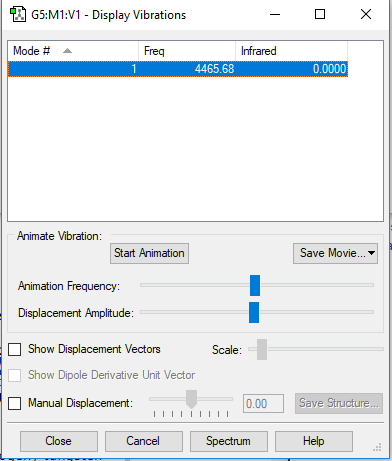
Display Vibrations
| Mode | wavenumber (cm-1) | symmetry | Intensity (au) | Image |
|---|---|---|---|---|
| 1 | 4466 | SGG | 0 | 
|
No. of expected modes (3N-5) = 1
No. of bending = 0
No. of stretching=1
No. of IR Bands= 0, there is no change in dipole moment therefore no bands visible
Charge Analysis
• 0 was the expected charge as the atoms in this diatomic molecule are the same, therefore have the same electronegativity values
Nitrogen
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| E(RB3LYP) | -109.52412868 au |
| RMS Gradient | 0.00000060 au |
| Point Group | D*H |
| N-N Bond Distance | 1.11 ± 0.01 Å |
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES Predicted change in Energy=-3.401042D-13
Nitrogen Molecule |
The optimisation file is linked to here
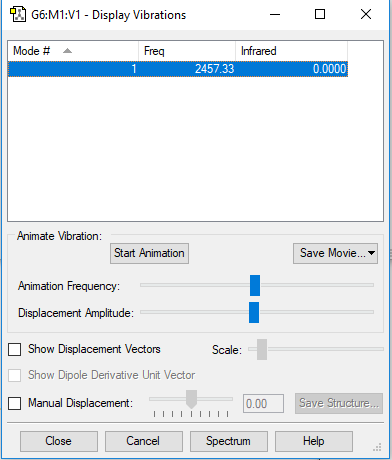
Display Vibrations
]]
| Mode | wavenumber (cm-1) | symmetry | Intensity (au) | Image |
|---|---|---|---|---|
| 1 | 2457 | SGG | 0 | 
|
No. of expected modes (3N-5) = 1
No. of bending = 0
No. of stretching=1
No. of IR Bands= 0, there is no change in dipole moment therefore no bands visible
Charge Analysis
• 0 was the expected charge as the atoms in this diatomic molecule are the same, therefore have the same electronegativity values
Mono-metallic Transition Metal complex with N2 : (Dinitrogen-N)-(bis(di-t-butlyphosphinomethyl(dimethyl)silyl)amino)-rhodium(i)
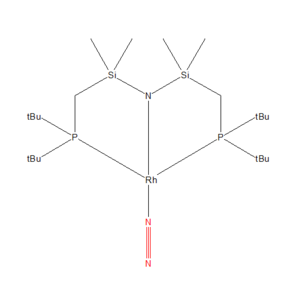
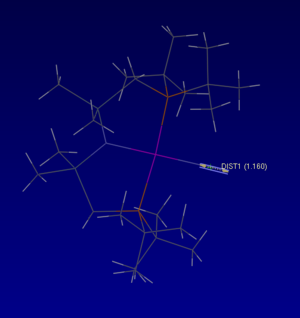
The CCDS file is linked to here
•This complex has the unique identifier of DIVEP
•It is light brown in colour, with the formula C22H52N3P2RhSi2. The N2 acts as an 'end on' ligand.
• It has an experimentally determined dinitrogen bond length of 1.160 Å. The computational calculated N-N bond length was 1.11 ± 0.01 Å, the lengths are similar however, the experimentally observed bond length is slightly longer. As such the dinitrogen bond is weaker.
• The bond length found via optimisation of the molecule using Gaussian was an approximation, correct to around 0.01 Å. So, the experimentally determined bond lengths whilst close in length to the optimisation, would be longer and therefore weaker due to the coordination complex formed with Rhodium. This is because of the sharing of electrons between the Rhodium and Nitrogen atoms, that form an interaction creating the metal-ligand complex. The Rhodium atom withdraws electron density from the dinitrogen bond weakening it.
• There also could be error in the calculation method, in that quantum mechanical calculations are being used to approximate the physical world, which will give discontinuities.
The Haber-Bosch Process
• The Haber-Bosch process is an industrial process used to produce ammonia using gaseous nitrogen and hydrogen. Ammonia is a useful resource, particularly as a fertiliser for agricultural purposes.
N2 + 3H2 → 2NH3
| E(NH3) | -56.55776873 au |
| 2*E(NH3) | -113.11553746 au |
| E(N2) | -109.52412868 au |
| E(H2) | -1.17853936 au |
| 3*E(E(H2)) | -3.53561808 au |
| ΔE = 2*E(NH3)-[E(N2) + 3*E(H2)] | -0.0557907 au = -146.4784829 kJ/mol |
Due to the reaction being exothermic the ammonia is the more stable compound than the gaseous reactants combined.
Part 4/5: CH4 Molecule
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| E(RB3LYP) | -40.52401404 au |
| RMS Gradient | 0.00003263 au |
| Point Group | Td |
| C-H Bond Distance | 1.09 ± 0.01 Å |
| H-C-H Bond Angle | 109 ± 1 ° |
Item Value Threshold Converged? Maximum Force 0.000063 0.000450 YES RMS Force 0.000034 0.000300 YES Maximum Displacement 0.000179 0.001800 YES RMS Displacement 0.000095 0.001200 YES Predicted change in Energy=-2.256043D-08 Optimization completed.
Methane Molecule |
The optimisation file is linked to here
Display Vibrations
| Mode | wavenumber (cm-1) | symmetry | Intensity (au) | Image |
|---|---|---|---|---|
| 1 | 1356 | T2 | 14 | 
|
| 2 | 1356 | T2 | 14 | 
|
| 3 | 1356 | T2 | 14 | 
|
| 4 | 1579 | E | 0 | 
|
| 5 | 1579 | E | 0 | 
|
| 6 | 3046 | A1 | 0 | 
|
| 7 | 3162 | T2 | 25 | 
|
| 8 | 3162 | T2 | 25 | 
|
| 9 | 3162 | T2 | 25 | 
|
No. of expected modes (3N-6) = 9
No. of bending = 5 (1,2,3,4,5)
No. of stretching= 4 (6,7,8,9)
No. of expected IR Bands= 0, there is no change in dipole moment so no clear bands visible
Charge Analysis
• The carbon atom is negatively charged as it is more electronegative than hydrogen, hence more electron withdrawing than the hydrogen atoms. Leaving the hydrogen atoms with a corresponding positive charge as the negatively charged bonding electrons are 'pulled' closer to the carbon atom. However, due to the symmetric nature of the tetrahedral structure overall there is no net polarity, even if there is an electronegativity difference in the individual bonds.
Molecular orbitals
| Image | Description |
|---|---|
 |
Energy= -10.16707
This orbital is the lowest in energy. It will not have an effect on bonding as it is too deep in energy. The largest contribution is from the 1s AO on the carbon atom. |
 |
Energy= -0.69041
This orbital is an occupied molecular bonding orbital. It has no nodes and the electrons are distributed evenly among all atoms. This will have an effect on bonding. The AO contribution is mostly from the 2s/3s on carbon and the 1s AO on the hydrogen atoms. |
 |
Energy= -0.38831
This orbital is an occupied molecular bonding orbital. It is a mixture of bonding and anti-bonding orbitals, shown by the node separating the phases. This produces 3 degenerate molecular orbitals, for molecular orbitals 3, 4, 5. These represent the HOMO of the methane molecule. This will have an affect on bonding. There is a large contribution from the 2p orbital on carbon and the 1s AO on the hydrogens. Where 2 1s AO of the hydrogens have added in phase with the 2p orbital on the carbon, as well as 2 out of phase. |
 |
Energy= 0.11824
This orbital is an unoccupied mixture of bonding and anti-bonding orbitals. This is in the LUMO region. The contribution of the orbitals is mostly from the 3s and 2s on the carbon and the 1s and 2s on the hydrogen. The 2s and 3s on the carbon are in the same phase, but opposite to the AOs on hydrogen. This will not have an effect on bonding. |
 |
Energy= 0.17677
This orbital is an unoccupied mixture of bonding and anti-bonding orbitals. This is high in energy. The largest contributions of AOS are from the p orbitals on carbon and the s on the Hydrogen atoms. This will not have an effect on bonding. |
The optimisation file is linked to here
Part 6ː Independent (Fluorine)
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| E(RB3LYP) | -199.49825218 au |
| RMS Gradient | 0.00007365 au |
| Point Group | D*H |
| F-F Bond Distance | 1.40 ± 0.01 Å |
Item Value Threshold Converged? Maximum Force 0.000128 0.000450 YES RMS Force 0.000128 0.000300 YES Maximum Displacement 0.000156 0.001800 YES RMS Displacement 0.000221 0.001200 YES Predicted change in Energy=-1.995025D-08 Optimization completed.
Fluorine Molecule |
The optimisation file is linked to here
Display Vibrations
| Mode | wavenumber (cm-1) | symmetry | Intensity (au) | Image |
|---|---|---|---|---|
| 1 | 1065 | SGG | 0 | 
|
No. of expected modes (3N-5) = 1
No. of bending = 0
No. of stretching=1
No. of IR Bands= 0, there is no change in dipole moment therefore no bands visible
Charge Analysis
• 0 was the expected charge as the atoms in this diatomic molecule are the same, therefore have the same electronegativity values
Marking
Note: All grades and comments are provisional and subject to change until your grades are officially returned via blackboard. Please do not contact anyone about anything to do with the marking of this lab until you have received your grade from blackboard.
Wiki structure and presentation 1/1
Is your wiki page clear and easy to follow, with consistent formatting?
YES
Do you effectively use tables, figures and subheadings to communicate your work?
YES
NH3 1/1
Have you completed the calculation and given a link to the file?
YES
Have you included summary and item tables in your wiki?
YES
Have you included a 3d jmol file or an image of the finished structure?
YES
Have you included the bond lengths and angles asked for?
YES
Have you included the “display vibrations” table?
YES
Have you added a table to your wiki listing the wavenumber and intensity of each vibration?
YES
Did you do the optional extra of adding images of the vibrations?
YES
Have you included answers to the questions about vibrations and charges in the lab script?
YES
N2 and H2 0.5/0.5
Have you completed the calculations and included all relevant information? (summary, item table, structural information, jmol image, vibrations and charges)
YES
Crystal structure comparison 0/0.5
Have you included a link to a structure from the CCDC that includes a coordinated N2 or H2 molecule?
NO - You linked a file instead of the CCDC entry of the TM complex. However, you gave an unique identifier instead. This identifier does not work on the CCDC structure search facility.
Have you compared your optimised bond distance to the crystal structure bond distance?
YES
Haber-Bosch reaction energy calculation 0.5/1
Have you correctly calculated the energies asked for? ΔE=2*E(NH3)-[E(N2)+3*E(H2)]
YES
Have you reported your answers to the correct number of decimal places?
NO - Energies in kJ/mol should only be reported up to one decimal place.
Do your energies have the correct +/- sign?
YES
Have you answered the question, Identify which is more stable the gaseous reactants or the ammonia product?
YES
Your choice of small molecule 3.5/5
Have you completed the calculation and included all relevant information?
YES
Have you added information about MOs and charges on atoms?
YES
2 bands would be expected for CH4 because the vibrations at 1356 and 3162 cm-1 have intensities greater than 0. The first MO could have been labelled as non-bonding and you missed to state its occupancy. MO3 is only bonding. A change in phase does not necessarily mean a MO is anti-bonding. The same is true for MOs 4 and 5. Both of them are only anti-bonding. You could have explained the relative MO energies.
Independence 1/1
If you have finished everything else and have spare time in the lab you could:
Check one of your results against the literature, or
Do an extra calculation on another small molecule, or
Do some deeper analysis on your results so far