Rep:Mod:WLL12Physicalcomplab

Introduction

In this computational experiment, the Cope rearrangement of 1,5-hexadiene and two examples of Diels-Alder cycloaddition reaction were investigated. The structures of the transition state of these reactions are the focus of study. The geometry and energies of the transition structures were analysed. The Molecular orbitals of the reactants and transition states for the Diels-Alder reactions were studied in order to understand their interactions and the geometries of the transition structures. All molecules were modelled using GaussView 5.0 and all calculation was done by the Gaussian program.

Gaussian applies the Born-Oppenheimer Approximation in which the nuclei is much heavier than the electrons and hence the motion of nuclei and electrons can be treated separately. A potential energy surface (PES) is created based on this approximation. It represents the potential energy as a function of the internuclear distance in a reaction. The use of different method and basis set for the calculation would affect the accuracy of the results compared to experimental data. These are discussed in the following sections.

The Cope Rearrangement Tutorial

Optimisation of 1,5-Hexadiene

Table 1 Optimised structure of 1,5-hexadiene

	Optimised "anti" 1,5-hexadiene molecule	Optimised "gauche" 1,5-hexadiene molecule
Jmol
Method/Basic set	HF/3-21G	HF/3-21G
Energy (a.u.)	-231.6853962	-231.6926612
Point group	C2h	C1

Figure 1. Newman projection of conformers of 1,5-hexadiene. a) "Anti" structure, C₂h. b) "Gauche" Structure, C1

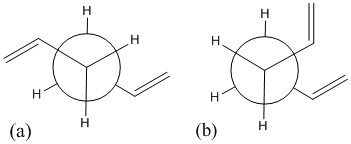
The free rotations about the C-C single bonds give rise to many possible conformations in 1,5-hexadiene. Table 1 shows two optimised 1,5-hexadiene molecules. One is antiperiplanar and the other is gauche. By comparing to Appendix 1, they are anti 3 and gauche 3. It was predicted that the 1,5-hexadiene with gauche linkage at the centre of the molecule would have a higher energy then the "anti" structure. The vinyl groups at the end of hexadiene are closer together in the gauche structure than in the "anti" structure. The gauche structure has a dihedral angle of 60 degree at the centre and repulsive steric interaction was expected to result in an increase in energy.

However, it was shown that the "anti" 1,5-hexadiene has a higher energy compared to the gauche conformer which has a slightly lower energy. By comparing to the table shown in Appendix 1, it was also found that the C₁ gauche conformer is the lowest energy conformation of 1,5-hexadiene.

A possible explanation to this is that the gauche structure is stabilised by an attractive interaction between the protons on one vinyl group and the π-orbital on the other. A vinyl proton is covalently bonded to a carbon atom and weakly interacting with the π-orbital of the double bond. This is known as the CH/π interaction . In the antiperiplanar structure (Fig. 1a), such interaction is not possible as the vinyl groups are far apart. In the gauche structure (Fig. 1b), the vinyl groups are close to each other and therefore it is stabilised by this interaction.

1,5-hexadiene with an "anti" linkage, C_i conformation

Table 2 Optimised structure of "anti" 1,5-hexadiene, C_i

Method/basis set	HF/3-21G	DFT/6-31G*
Jmol
Labelled molecule
Energy (a.u.)	-231.695353	-234.559704

The C_i "anti 2" 1,5-hexadiene optimised at the HF/3-21G level of theory has an energy of -231.6925353 au. This value is the same as the one given in Appendix 1. This was subsequently re-optimised at B3LYP/6-31G* level and yielded a lower energy form than the one at HF/3-21G level. The structure from the HF/3-21G calculation closely resembles that from B3LYP/6-31G* calculation. Table 3 summarizes the dihedral angles and the bond lengths of both structures. The centre dihedral angle and all carbon-carbon bond lengths are similar in both 1,5-hexadiene. There is only a 4 degrees difference in the terminal dihedral angle between them. Overall, the change in geometry is minimal.

Table 3 Geometry data "anti" 1,5-hexaidene optimized at HF/3-21G and DFT/6-31G* level; C_i

Method	HF			DFT
Dihedral angle(C1-C4-C6-C9);(º)	114.7			118.8
Dihedral angle(C4-C6-C9-C12);(º)	180.0			180.0
	C1-C4	C4-C6	C6-C9	C1-C4	C4-C6	C6-C9
Bond length(Å)	1.07	1.33	1.51	1.09	1.34	1.51

Frequency Analysis of "anti" 1,5-hexadiene, C_i conformation; DFT/6-31G

Figure 2 Vibrational Spectrum of "anti" 1,5-hexadiene

Frequency analysis was carried out. It gives the second derivative of the potential energy surface. If all frequencies are positive, it means a minimum was resulted. The absence of imaginary (negative) frequencies shows that the structure is optimized to a minima. Table 4 shows the thermochemical analysis of the optimized structure.

Table 4 Summary of energy

	Energy (in hatree)
Sum of electronic and zero point energies (E = Eelec + ZEP), at 0 K	-234.469215
Sum of electronic and thermal energies (E = E + Evib + Erot + Etrans), at 298.15 K and 1 atm	-234.461867
Sum of electronic and thermal enthalpies+	-234.460922
Sum of electronic and thermal free energies++	-234.500800

⁺ An additional correction for RT(H = E + RT) (Under which conditions is this expression for the enthalpy correct? João (talk) 12:03, 16 February 2015 (UTC))

⁺⁺ Including entropic contribution to the free energy (G = H-TS) (Any idea how the entropy is estimated in this case? João (talk) 12:03, 16 February 2015 (UTC))

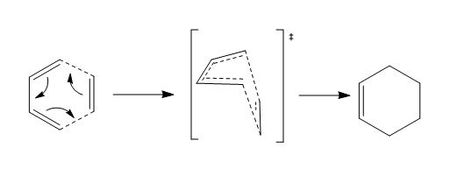
Optimization of "Chair" Transition Structures

The Cope rearrangement have two different transition state: Chair and Boat.

Optimisation and Frequency Analysis of Chair Transition Structure (Opt+Freq)

An allyl fragment (CH₂CHCH₂) was first optimised to TS(Berny) at HF/3-21G level. Two optimised fragments were arranged in the chair form and underwent optimisation and frequency analysis. This optimised structure has an imaginary frequency at -818 cm^-1. The negative second derivative of the potential energy surface corresponds to a maxima. This shows that the optimisation of the chair transition state structure was successful. The imaginary frequency was also animated in table 5.

Table 5 Results of optimisaed chair transition structure

Jmol	Animated vibration at -818 cm-1			Vibrational spectrum
(3-21G) optimised chair transition state

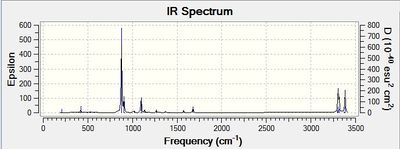
Alternatively the frozen coordinate method was used to optimise the transition structure. This was done by fixing the distance between the terminal carbons from both allyl fragments to 2.2 Å and then optimised to a minimum (HF/3-21G). A transition state optimisation to TS(Berny) was carried out subsequently at HF/3-21G level. This allows the bond forming/breaking distances between the two fragments to be optimised as well (Did you confirm the existance of an imaginary frequency in this case as well? João (talk) 12:03, 16 February 2015 (UTC)). The table below summarizes the geometry data of the transition structures that were optimised differently.

Both optimised transition structures with either frozen or optimized bond forming/breaking distances, show similar C-C bond length and C-C-C angle within one allyl fragment. These are also similar in values compared to the structure from "Opt+Freq" calculation. The main difference lies in the distance between C1-C6 and C3-C4. When the bond forming/breaking distances were optimised, these values are more similar to that in the structure from "Opt+Freq" calculation. This shows that freezing the coordinate would give a less accurate optimisation of structure. (Does the structure labeled Opt(Freeze Coordinate) below correspond to a transition state? Does it have a zero gradient? João (talk) 12:03, 16 February 2015 (UTC))

Table 6 Geometry data of optimised chair transition structure

	Bond length (C1-C2)(Å)	Angle (C1-C2-C3)(º)	Distance between (C1-C6) (Å)	Distance between (C3-C4) (Å)
Opt + Freq	1.39	120.5	2.02	2.02
Opt(Freeze Coordinate)	1.39	121.8	2.16	2.20
Opt(Derivative)	1.39	120.5	2.02	2.02

Optimization of "Boat" Transition Structures

Figure 3. First attempt of QST2 calculation

Figure 4. Rearrangement of butadiene

Figure 5. Cope Rearrangement

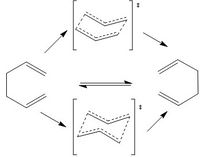The previously optimised C_i "anti" 1,5-hexadienes were optimised to a transition state and frequency analysis were carried out using the QST2 method. QST2 requires reactant and product as the input and all atoms must be labelled in the same way in both structure. The first calculation was done without any modification to the structure orientation. The job was failed and resulted in the transition structure shown in figure 3 (In which sense did the calculation fail? João (talk) 19:06, 16 February 2015 (UTC)). The 1,5-hexadiene molecules were re-orientated so that they had the same arrangement as what shown in figure 4. The modified molecules had a dihedral angle of 0 degree at the centre and 100 degrees for the inside C-C-C angle. The QST2 calculation of the modified structure was successful and the following results (table 7) were obtained. The distance between the two fragments is 2.14 Å. The boat transition structure was optimized and it has an imaginary frequency at -840 cm^-1.

The optimisation was also carried out using the QST3 calculation. This requires 3 inputs in the following order: the reactant, product, and guess transition state structures. Similar to QST2, the atoms must be labelled in the same order. The energy and geometry of the optimized structure of QST3 calculation resembles that of QST2 (What do you conclude from that? João (talk) 19:06, 16 February 2015 (UTC)). It also has an imaginary frequency at -840 cm^-1.

Table 7 Results of optimised boat transition structure

Jmol	Vibration at -840 cm-1			Vibrational spectrum
(3-21G) optimised boat transition state

Intrinsic Reaction Coordinate (IRC) Method

Table 8 Results of IRC calculation

First Calculation	Total Energy along IRC	RMS Gradient Norm along IRC
No. of points along IRC: 50

It is difficult to predict which conformers of 1,5-hexadiene will form from the chair and boat transition structures. Intrinsic Reaction Coordinate (IRC) method was used to find out the structure that has the lowest energy (Do you then expect to obtain the gauche3 structure? Why don't you? João (talk) 19:06, 16 February 2015 (UTC)). It allows the lowest energy reaction path from the transition state towards the reactants and products to be followed. Only the forward direction of the reaction coordinate was considered here. The number of data points along the IRC was set to 50 and the force constant was set to "calculate always" in the first attempt. Forty-four intermediates were obtained. A second attempt of IRC calculation with 100 points was carried out to ensure the minimum energy geometry was reached (If your previous calculation converged after 44 steps, why did you increase the step number? João (talk) 19:06, 16 February 2015 (UTC)). There was no change to the energy graph and the gradient was closed to zero at the end of calculation. These prove that a minimum geometry has reached. A gauche conformer with an energy of -231.691608 a.u. (gradient: 0.00015154 a.u.) was found to be the minimum geometry from this calculation. This is gauche 2 in Appendix 1.

Optimisation of Chair and Boat Transition structures using B3LYP/6-31G*

The HF/3-21G optimised chair and boat structure were re-optimised using B3LYP/6-31G* method. The following tables present a comparison for the geometries and different energies values. The chair transition structures optimised at HF/3-21G and B3LYP/6-31G* have very similar geometry compared to each other. The same applies to the boat transition structure (Did you check you still had a transition state at this level of theory? João (talk) 19:06, 16 February 2015 (UTC)). However, the energies are lower for the transition structures optimised at B3LYP/6-31G* level.

Table 9 Geometry data of chair and boat transition structure

	HF/3-21G			B3LYP/6-31G*
	Bond length (C1-C2)(Å)	Angle (C1-C2-C3)(º)	Distance between (C1-C6)/(C3-C4) (Å)	Bond length (C1-C2)(Å)	Angle (C1-C2-C3)(º)	Distance between (C1-C6)/(C3-C4) (Å)
Chair TS (Top)	1.38	122.0	2.20	1.39	122.0	2.20
Boat TS (bottom)	1.41	121.2	2.14	1.39	121.1	2.14

Table 10 Summary of Energy (in hatree)

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies (0 K)	Sum of electronic and thermal energies (298.15 K)	Electronic energy	Sum of electronic and zero-point energies (0 K)	Sum of electronic and thermal energies (298.15 K)
Chair TS	-231.619332	-231.466702	-231.461343	-234.553938	-234.413269	-234.406982
Boat TS	-231.602802	-231.450928	-231.445299	-234.542868	-234.401492	-234.395284
Reactant (Ci; Anti)	-231.692535	-231.539539	-231.532565	-234.611712	-234.469215	-234.461867

Calculation of Activation Energies for Both Transition Structures

Table 11 Summary of Activation Energy (in kcal/mol)

	HF/3-21G		B3LYP/6-31G*		Experimental value from Appendix 1
Temperature	0 K	298.15 K	0 K	298.15 K	0 K
∆E (Chair)	45.70	44.69	35.12	34.44	33.5 ± 0.5
∆E (Boat)	55.78	54.93	42.50	41.91	44.7 ± 2.0

The boat transition structure was found to have a higher activation energy than the chair. This can be due to the unfavourable repulsive interaction between the protons in the structure. The activation energies at 0 K of both transition structures optimised at B3LYP/6-31G* level are more similar to the experimental values . This can be explained by the choice of method and basis set. Electronic structure methods such as Hartree-Fock (HF) or Density functional theory (DFT) all approximate the exact solution in some ways. Generally, the lower the energy structure after a geometry optimisation, the more suited the method is to describe the ground state. (This would be true if the method obeys the variational principle. Is that the case for both methods you used? In general, one cannot compare absolute energies calculated with different methods as they often use different references. João (talk) 19:06, 16 February 2015 (UTC))

The HF approximation describe non-interacting electrons under the influence of a mean electron field potential (If electrons interact with the mean field of other electrons, electrons are interacting. João (talk) 19:06, 16 February 2015 (UTC)). It also accounts for the Pauli exclusion principle. DFT takes into account the electron correlation, but not the Pauli exclusion principle (In which way does DFT not obey the exclusion principle? João (talk) 19:06, 16 February 2015 (UTC)). The fact that electrons interaction is considered in the calculation gives a better approximation to strongly correlated problems. Different basis sets uses different number of functions to describe each atomic orbital and hence would affect the accuracy of calculation. The 6-31G* is a larger basis set compared to 3-21G in which more gaussian functions are used to describe each atomic orbital. 6-31G* also takes into account the distortion (polarisation) of the orbitals when molecules are formed. This in turn enables the basis set to describe the wavefunction more accurately.

The Diels Alder Cycloaddition

Optimisation of cis-butadiene and Molecular Orbitals Analysis

Figure 6 Diels Alder reaction of ethene and cis-butadiene

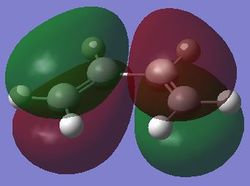
Ethene and cis-butadiene were optimised to a minimum using the AM1 semi-empirical method. Their corresponding HOMO and LUMO were plotted as shown in table 12 and 13. The plane of symmetry bisect the C=C bond in ethene and centre C-C in butadiene.

Table 12 Ethene MO

HOMO, symmetric with respect to the plane	LUMO, antisymmetric with respect to the plane

Table 13 Cis-butadiene

Jmol	HOMO, antisymmetry with respect to the planne	LUMO, symmetric with respect to the plane
(AM1)optimised cis butadiene

Table 14 Diels Alder Transition State

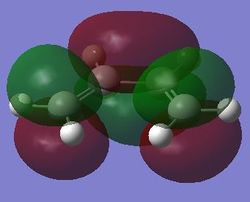
Jmol	Vibration at -956 cm-1	Vibration at 147 cm-1
(AM1)optimised Diels Alder transition state

The imaginary frequency at -956 cm^-1 corresponds to the bond forming/breaking of the Diels-Alder reaction. The animated vibration motion (table 14) shows that the bonds are formed synchronously. The lowest positive frequency does not show the same movement, and bonds do not seem to be forming or breaking.

Table 15 Diels Alder Transition State MO

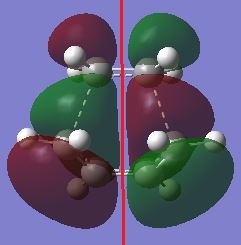
HOMO, Antisymmetry with respect to the plane	LUMO, symmetric with respect to the plane

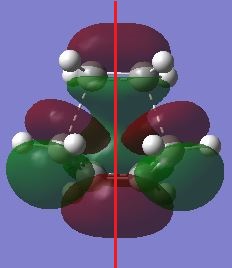
The Woodward–Hoffmann rules apply to cycloaddition reaction. It explains the stereochemical outcome of pericyclic reactions by considering the symmetry of the ‘frontier orbitals’ that contribute to the formation and breaking of bonds. A cycloaddition reaction involves the concerted formation of two or more σ bonds between the termini of two or more conjugated π systems. In Diels Alder reactions, two π systems are involved. The highest occupied molecular orbital (HOMO) of the dienophile overlaps with the lowest unoccupied molecular orbital (LUMO) of the diene. The diene contributes 4π electrons, and the dienophile contributes 2π electrons. This gives a total count of 6 electrons and hence the reaction is called [4πs + 2πs] cycloaddition. The reaction is thermally allowed and proceed suprafacially (new bonds form on the same face at both ends) via Hückel topology since it has 4n+2 (n=1) electrons in the system. Similarly, the Dewar and Zimmerman rules states that favourable pericyclic reactions will proceed via an aromatic transition state. If the reaction has a 4n+2 suprafacial topology, it is a Hückel system and reaction is allowed.

The reaction is favored by electron-donating groups such as COR, COOR and CN on the dienophile as this will lower the energy of LUMO. An electron-rich diene is also favoured. These would decrease the energy gap between the HOMO and LUMO. Since butadiene and ethene are discussed here, the effect of substituents is ignored.For an allowed reaction, the orbitals that overlap must have the same symmetry. The antisymmetric HOMO of butadiene interests with the antisymmetric LUMO of ethene to give rise to the antisymmetric HOMO of the transition state. Similarly, the same applied to the LUMO of the transition state. The symmetric HOMO of ethene overlaps with the symmetric LUMO of butadiene to form the symmteric HOMO of the transition state.

Table 16 Geometry data of optimised Diels Alder transition structure

Bond length (C1-C2),(C3-C4)(Å)	Bond length (C2-C3)(Å)	Distance between (C4-C5),(C1-C6) (Å)	Distance between (C5-C6) (Å)
1.38	1.39	2.12	1.38
Typical sp 3 bond length (Å): 1.54		Typical sp 2 bond length (Å): 1.34
van der Waals radius of C atom (Å): 1.70

The distances of the bond forming/breaking in the transition structure are 2.12 Å. These distances are much greater than the sp² and sp³ hybridised C-C bond. They are shorter than twice the van der Waals radius for carbon (3.40 Å) and are not close enough to experience repulsive interaction towards each other (Could it be attractive though? João (talk) 19:06, 16 February 2015 (UTC)). Hence bond formation is favourable.

Table 17 Results of IRC (No. of points: 60)

Energy of product(a.u.): 0.0746648	Final gradient: 0.0005776

An IRC calculation was carried out. This time, both direction was run. The energy graph (table 17) shows an expected reaction coordinate. A minimum geometry in the forward direction has an energy of 0.0746648 a.u. and a gradient close to zero. Increasing the number of data points to 70 made no difference to the results. This proves that a minimum geometry has reached. (It just confirms that your first calculation had converged. João (talk) 19:06, 16 February 2015 (UTC))

Cyclohexadiene-1,3-diene Reaction with Maleic Anhydride

The AM1 semi-empirical method was applied for all calculation in this session. Maleic anhydride and cyclohexa-1,3-diene were optimized to a minimum. There HOMO and LUMO were plotted in table 18.

Table 18 HOMO and LUMO of Maleic Anhydride and Cyclohexa-1,3-diene

Maleic Anhydride		Cyclohexa-1,3-diene
HOMO	LUMO	HOMO	LUMO

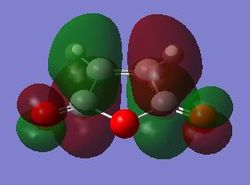
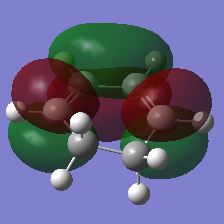
The reactants were rearranged into a guess structure that resembles the exo transition state. They were optimised to TS(Berny) by freezing the coordinates and subsequently unfrozen. Frequency analysis was carried out. The imaginary frequency at -812 cm^-1 confirms that a transition state was optimized.

Table 19 Exo Transition State

Jmol	Vibration at -812 cm-1	HOMO
optimised exo transition state

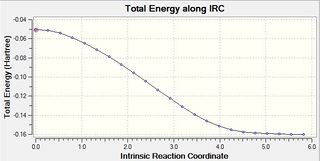
IRC calculation was carried out for the exo transition structure and yielded the following results:

Table 20 Results of IRC of Exo Transition Structure, No. of data points: 40

Energy of the product (a.u.): -0.160168	Gradient: 0.0001171

(In this case the IRC should have two non-equivalent branches. What happens in the other branch? João (talk) 19:06, 16 February 2015 (UTC))

The reactants were rearranged into the endo transition state. They were optimized to TS(Berny) by freezing the coordinates and subsequently unfrozen. Frequency analysis was carried out. The imaginary frequency at -806 cm^-1 confirms that a transition state was obtained.

Table 21 Endo Transition State

Jmol	Vibration at -806 cm-1	HOMO
(AM1) optimised exo transition state

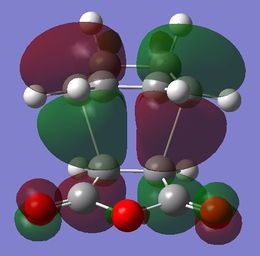
IRC calculation was carried out for the endo transition structure and yielded the following results (table 22). The gradient did not reach a value close to zero upon first calculation (middle). Another IRC calculation was run from the last point of the first calculation and yields results shown on the left hand side and right hand side (The idea of continuing the IRC is not bad, but you need to be a bit careful in doing so. Did you instruct the program that you were doing an IRC continuation? By default the IRC is started along the imaginary frequency mode, but in this region of the potential energy surface you likely don't have an imaginary frequency. You can instruct the program to follow the gradient instead, did you do that? João (talk) 19:06, 16 February 2015 (UTC)). This shows that the minimum geometry was found. (How did you confirm this? João (talk) 19:06, 16 February 2015 (UTC))

Table 22 Results of IRC of Endo Transition Structure, No. of data points:20

Energy of product (a.u.): -0.159874	Gradient along IRC of first calculation	Gradient:0.00002890

Table 23 Geometry data and energy of Exo and Endo transition structure

	Bonding forming distance (C2-C8),(C5-C7)(Å)	Orientation (C3-C9),(C4-C11)(Å)	Maleic anhydride C=O bond length (Å)	Maleic anhydride C-C bond length (C7-C8)/(C8-C9)(Å)	Cyclohexadiene C-C bond length(Å)	Cyclohexadiene C=C bond length(Å)	Energy (a.u.)
Exo TS(Top)	2.17	2.95	1.22	1.41/1.49	1.39/1.49	1.39	-0.0504198
Endo TS (bottom)	2.16	2.89	1.22	1.41/1.49	1.39/1.49	1.39	-0.0515048

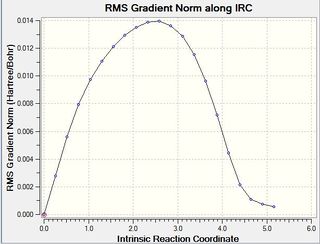
Analysis

Figure 7 Reaction scheme of Diels-Alder reaction of cyclohexadiene-1,3-diene with Maleic Anhydride

In cycloaddition, two new bonds are formed at the same time. Two filled p orbitals and two empty p orbitals need to be arranged at the right place and with the right symmetry in order to interact. In this Diels-Alder reaction, the LUMO of electron poor anhydride interacts with the HOMO of the diene. A node is present at the middle of HOMO of the diene and same in LUMO of dienophile. By Woodward–Hoffmann rules, it is an allowed interaction. The interaction of LUMO of diene and HOMO of anhydride also have the correct symmetry but due to the larger energy gap between them, it is less favourable. The HOMO of the diene and the LUMO of dienophile are closer in energy and gives a better overlap.

Figure 8 Second orbital overlap effect of Diels-Alder reaction of cyclohexadiene-1,3-diene with Maleic Anhydride. a)Through space interaction between C=O and the back of diene. b)Primary and secondary orbital overlaps in endo structure. c) Overlap of orbitals in exo structure

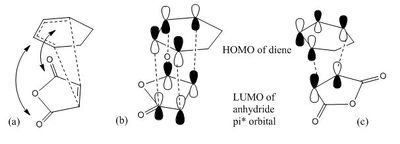
Second orbital overlap effect was proposed by Woodward and Hoffmann. It is the positive overlap of inactive orbitals in the frontier molecular orbitals of a pericyclic reaction. In the endo transition structure (Figure 8b), it has the primary orbital overlap in which the p-orbitals of the anhydride LUMO interacts with the diene HOMO. However, the p-orbital on both side of the C=O also interacts with the p-orbitals at the back of the diene. These interactions are descriped as secondary as there are no change in the bonds. They interact strongly in the endo transition state (Figure 8a) but such interaction is not possible in the exo transition state (Figure 8c). The secondary overlap gives a stabilizing effect in the endo structure irrespective of the energies of the HOMO and LUMO. (Wouldn't such and effect influence the orbital energy? João (talk) 19:06, 16 February 2015 (UTC))

Table 23 shows a comparison of structure and energy of the two transition structure. In general, both structures resemble each other. The main difference lies in the through space distance (Orientation distance) between the -(C=O)-O-(C=O)- fragment of maleic anhydride and the C atoms of -CH₂-CH₂- in exo and -CH=CH- in endo . This distance is closer in endo. The endo structure also has a lower energy than the exo. These provides evidence that the endo structure is stabilized by the secondary overlap. Another way of analysing the presence of secondary overlaps, is to look at the MOs of the transition structure.

Table 24 MOs of Endo and Exo Transition Structure

	HOMO - 4	HOMO	LUMO	LUMO + 1	LUMO + 2
Endo TS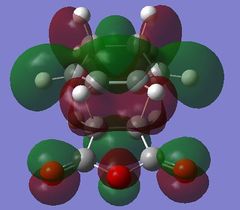
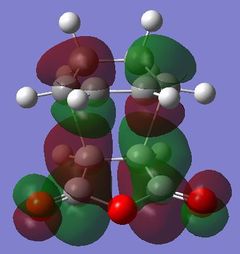
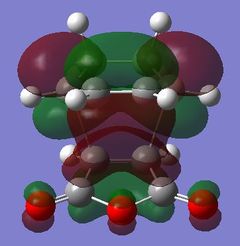
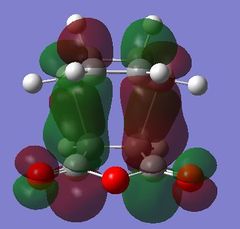
Exo TS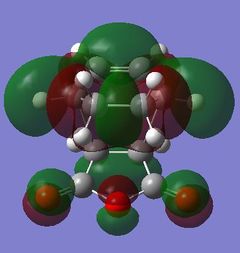

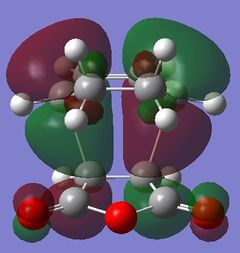
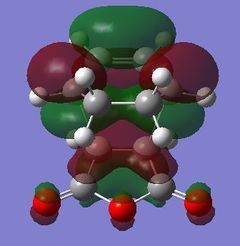
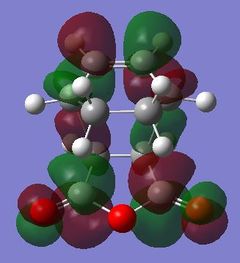
Table 24 shows a comparison of several MOs from the endo and exo transition state. The secondary orbitals overlap was not observed in the HOMO nor LUMO of the endo structure. The interaction was present in the HOMO-4, LUMO+1 and LUMO+2 instead. This is possibly due to the fact that orbital mixing was not taken into account in the calculation. A high level of theory such as HK or DFT might give a result closer to expectation. In the exo transition structure, no secondary orbitals overlap was observed which correlates with the discussion above.

Despite having endo form as the lower energy transition structure, it was shown that it leads to a higher energy product. Table 20 and table 22 shows the result of the IRC calculation. The energy of the endo product has an energy of -0.159874 a.u. where and the energy of the exo product has an energy of -0.160168 a.u.. This shows that the endo product is less stable. The structure experience steric repulsive interaction between the alkene of the six membered ring and the carbonyl groups of the dienophile. In an irreversible Diels-Alder reactions, therefore it would be the kinetic product of the reaction. The kinetic product is formed faster. If the reaction is under kinetic control, the energies of the transition states would dictate the outcome of the reaction. By Hammmond's postulate, the starting material, intermediate or product closest in energy to the transition state of the interest will be similar in structure.

The semi-empirical method was a simplification of the HF theory therefore it offers a much faster calculation for large molecules compared to HF and DFT method. However, the accuracy of this method might not be high for other systems. AM1 is a modified model of the 'Modified Neglect of Diatomic Overlap' (MNDO) model. MNDO uses only s and p orbital basis sets. AM1 model considers the nuclear-nuclear core repulsion and hence the van der Waals interactions. However, this model may over-estimate the system and result in miscalculation of the geometry of molecules. This may also be the reason that secondary orbitals overlap was not observed in the HOMO or LUMO of the endo transition state. (I do not quite follow the argument in the last 3 sentences, and its implications. João (talk) 19:06, 16 February 2015 (UTC))

Conclusion

All molecules were optimised successfully. For 1,5-hexadiene, the frozen coordinate method was found to be the most accurate way of optimising the strucutre. The chair transition structure is has a lower energy than the boat transition structure due to having less steric repulsion. The gauche 1,5-hexadiene was confirmed to be the lowest energy conformer. It was found that the DFT/B3LYP/6-31G* method and level of theory was found to be the most accurate among all the method used.

In the Diels-Alder cycloaddition, an allowed reaction requires a matching symmetry from both reactants. the Woodward-Hoffmann rule was discussed in detailed. In the reaction of cis-butadiene and ethene, the symmetric HOMO of ethene interacts with the symmetric LUMO of butadiene. In the reaction of cyclohexa-1,3-diene and maleic anhydride, the same rule applies. The endo transition structure was found to be the lowest energy form but the endo product was in fact the kinetic products. The secondary orbitals overlap effect played an important role when determining the energies of the transition structures. However, the AM1 semi-empirical method was not accurate enough to simulate this. Owning to time constrain, the calculation was not carried out using different method.