Rep:Mod:WGW1993phys3

The Cope Rearrangement

Introduction

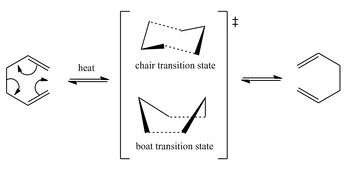
The Cope rearrangement, originally discovered by Arthur C. Cope, is a [3,3]-sigmatropic shift involving the migration of an allyl group. The reaction under investigation is the Cope rearrangement of 1,5-hexadiene, which is a thermally allowed six electron process that proceeds suprafacially. There are three extreme mechanistic pathways that have been proposed in the literature based on experimental and computational studies. Two of these mechanisms are in fact not concerted processes and involve the formation of radical intermediates: one via the formation of two allyl radicals and the other via the 1,4-cyclohexanediyl diradical. The third mechanism involves the formation of an aromatic transition state in a concerted process. Though the first two mechanisms have been observed in more substituted molecules, for the case of 1,5-hexadiene it is currently accepted that a concerted mechanism operates. In addition, there are two possible transition state geometries for the Cope rearrangement: the chair form and the boat form. The chair form has been shown to be lower in energy due to its aromatic nature, whereas the boat transition state is non-aromatic.

In this study we aim to find and optimize the geometries of the most stable conformers of 1,5-hexadiene and use these structures to model the possible transition state geometries of the Cope rearrangement.

Optimizing the Reactants and Products

Finding the lowest energy conformer - anti or gauche?

The structure of 1,5-hexadiene was optimized at the HF/3-21G level of theory in order to find the lowest energy conformation. The point group, ground-state energy and conformation relative to the wiki page appendix are specified for each case in table 1.1. The first optimization was carried out using an anti-periplanar arrangement of the four central carbon atoms. This calculation yielded a conformer of Ci symmetry and was assigned as the anti2 conformer from its electronic energy. A second molecule was then constructed with a gauche interaction in the central four carbon atoms. The optimization of this structure gave a higher energy conformer with C2 symmetry. Taken simply, this result suggests that an anti-periplanar arrangement of the central four carbon atoms is more stable than a gauche arrangement. However, this conclusion does not take into account the rotation about bonds C2-C3 and C4-C5 which control the positions of the two terminal alkene groups.

It is known from conformational studies of straight chain alkanes that stability of a specific conformation is based on three key factors: σ/σ* overlap, bond-bond repulsion and van der Waals interactions. For short chain alkanes the maximization of σ/σ* overlap in the anti-periplanar arrangement of bonds dominates, though in medium and long chain alkanes the attractive van der Waals interactions between hydrogen atoms becomes more important. These attractive forces arise from gauche linkages and hence the tendency for longer alkane chains to fold back on themselves is known as the gauche effect. For 1,5-hexadiene, it was unclear what stabilising factor would predominate, though it was predicted that a more stable gauche conformation could be found. The third calculation attempted to increase the number of van der Waals contacts by positioning one of the alkene groups 'inwards' while maintaining a gauche arrangement for the central four carbons. This resulted in an even higher energy structure due to a repulsive interaction between two hydrogens 2.19 Å apart. With this knowledge, the final calculation yielded the most stable gauche structure: gauche3. The alkene groups were positioned in order to maximize van der Waals contacts while avoiding unfavourable steric clashes. Two key interactions set up were the A^1,3 eclipsed interactions between one of the alkene hydrogens and an alkyl hydrogen at each end of the molecule, which allowed for both effective σ/π* overlap of orbitals and an attractive interaction to form (d(H-H) = 2.43 and 2.45 Å).

It must be noted that while the gauche3 conformer was found to be the lowest in energy using the HF/3-21G method it is possible that a higher level of theory would suggest a different conformation as being the lowest energy.

Table 1.1 Optimization of four conformers of 1,5-hexadiene using HF/3-21G theory

Optimization	Structure	Point Group	Electronic Energy (hartrees)	Relative Energy (kcal/mol)	Conformation
1 - anti		Ci	-231.69253528	0.08	anti2
2 - gauche		C2	-231.69153032	0.71	gauche4
3 - gauche		C1	-231.68961573	1.91	gauche5
4 - gauche		C1	-231.61170280	0.00	gauche3

Optimization of the anti2 conformer - comparison of HF/3-21G and B3LYP/6-31G* theory

The anti2 structure optimized in the first set of calculations was reoptimized using the B3LYP/6-31G* method. This is a higher level of theory and hence more accurate results for the structure and energy are expected. Overall, the optimized structure of the anti2 conformer is very similar for both levels of theory. The point group remains as Ci and the dihedral angle as 180 degrees. However there are small differences in the bond lengths and angles. For example, B3LYP/6-31G* gave C=C bond lengths of 1.334 Å while HF/3-21G gave lengths of 1.316 Å. The increase in bond length at the higher level of theory also led to a widening of the C=C-C angles, from 124.8^o in HF/3-21G to 125.5^o.

Table 1.2 Summary of energies (in hartrees) of the anti2 conformer using HF/3-21G and B3LYP/6-31G* theory

Level of Theory	General Structure	Electronic Energy	Sum of Electronic and Zero-point Energies	Sum of Electronic and Thermal Energies	Sum of Electronic and Thermal Enthalpies	Sum of Electronic and Thermal Free Energies
HF/3-21G		-231.69253528	-231.539539	-231.532565	-231.531621	-231.570916
B3LYP/6-31G*		-234.61170280	-234.469204	-234.461857	-234.460913	-234.500778

A frequency calculation was also carried out for the anti2 conformer at both levels of theory. The key values obtained in this additional calculation were the 'the sum of electronic and zero-point energies' and 'the sum of electronic and thermal energies' which correspond to the potential energy at T = 0 K and T = 298 K respectively. These energies are used later in the calculation of the activation energies for the Cope rearrangement. On the other hand, 'the sum of electronic and thermal enthalpies' and 'the sum of electronic and thermal free energies' involve corrections for an RT term and entropic term respectively.

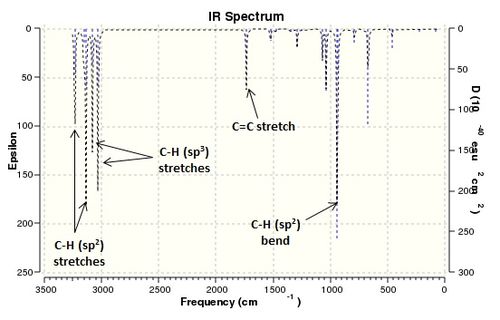
The frequency calculation also generated a list of vibrational modes for the anti2 conformer. The vibrations found using B3LYP/6-31G* theory are displayed below in an annotated IR spectrum.

Optimizing the Chair and Boat Transition State Structures

The chair and boat transition state structures were modelled using the HF/3-21G level of theory. The allyl fragment that features in both transition states was also optimized using the HF/3-21G method. The chair and the boat transition structures differ with respect to the orientation of the allyl group, resulting in the chair structure having C_2h symmetry and the boat C_2v symmetry. The chair structure was found to be 10.366 kcal/mol lower in energy than the boat structure and hence is in agreement with observations in the literature. Table 1.3 summarizes the output from the optimization and frequency calculations, including thermochemistry data to be used later in the calculation of activation energies.

Table 1.3 Optimizing the chair and boat transition structures for the Cope rearrangement using HF/3-21G theory

Transition Conformation	General Structure	Method	Distance between terminal allyl carbons (angstroms)	Imaginary Frequency (cm-1)	Electronic Energy (hartrees)	Sum of Electronic and Zero Point Energies (hartrees)	Sum of Electronic and Thermal Energies (hartrees)
Chair		Initial force constant	2.020	-817.86	-231.61932237	-231.466698	-231.461339
		Frozen coordinate	2.020	-817.78	-231.61932236	-231.466696	-231.461337
Boat		QST2	2.140	-839.94	-231.60280200	-231.450928	-231.445299
		QST3	2.140	-839.96	-231.60280247	-231.450928	-231.445299

Modelling the chair transition state geometry

The optimized allyl group was used to generate an initial guess structure for the chair transition state. The allyl groups were aligned in a chair conformation with the terminal carbon atoms of each group being separated by approximately 2.2 Å in space. This structure was then saved as a Gaussian input file to be used in two alternative optimization techniques.

Computing the force constants at the beginning of the calculation

This first method for optimizing the transition state involves computing the force constant matrix at the beginning of the calculation based on the initial guess structure. This technique only requires a single calculation and hence is quick to carry out however it does require a guess structure that is very similar to the optimized transition structure in order to locate the reaction coordinate.

An optimization and frequency calculation was carried out on the guess structure with the setting "Optimization to a TS (Berny)" and force constants calculated once. The optimized structure had a single imaginary frequency at -817.86 cm^-1 which corresponded to the σ-bond migration.

Freezing the reaction coordinate

The frozen coordinate method is an alternative way of generating the transition structure. It involves initially freezing the coordinates of the reacting centres and minimizing the energy of the rest of the guess structure before computing the Hessian of the system. Therefore, for the case of the Cope rearrangement of 1,5-hexadiene, the allyl fragments are first optimized while being frozen in space and then are unfrozen to allow for the optimization of the transition state. The advantage of this method is that it is often not necessary to compute the whole Hessian and hence time-consuming calculations involved in optimizing complex transition structures can be avoided.

As for the previous method, a guess structure was used as the starting point. The first step was to freeze the coordinates of the two pairs of carbon atoms involved in the bond breaking and bond forming processes. With this limitation in place, an optimization was then carried out specifying "Optimization to a minimum". The output of this calculation generated a structure that closely resembled that of the initial force constant method, but with the allyl fragments frozen at a distance of approximately 2.2 Å. The bonds previously frozen in space were unfrozen and were assigned the "Derivative" setting to provide spacial information for the calculation of the Hessian in this region. In addition, the force constants were specified to not be calculated.

The optimized structure generated was very similar to the structure generated by the previous method. In fact, the electronic energy, the imaginary frequency and the separation of the two allyl fragments were all found to be essentially identical for the two methods. This result agreed with what was expected, as the same level of theory should give the same structure and energy regardless of the method used, particularly for small systems as in the case of 1,5-hexadiene.

Modelling the boat transition state geometry

The QST2 method

The QST2 method uses the optimized structures of the reactant and product molecules to predict the structure of the transition state. The optimized anti2 conformer of 1,5-hexadiene generated in the first set of calculations at the HF/3-21G level of theory was used as both the reactant and product structures. The numbering of the atoms was then adjusted to correspond to a Cope rearrangement, as shown in the figure on the right. The QST2 calculation was then set up as an optimization and frequency calculation using the setting "TS (QST2)".

As expected, this first calculation failed to predict the boat transition structure, instead giving the more stable chair transition structure. To overcome this problem, the original input file was modified by changing the dihedral angle of the four central carbon atoms to 0^o and the internal C2-C3-C4 and C3-C4-C5 bond angles to 100^o. Using these structures as the new starting point, the QST2 calculation was re-run and this time was successful in locating the boat transition state. Again, as for the chair conformation, a single imaginary frequency was observed. The value for the boat transition state (-839.94 cm^-1) was found to be more negative than for the chair transition state (-817.86 cm^-1), indicating the presence of stronger interactions at the reacting centres in the former case. This is a direct result of the higher electronic energy of the boat structure relative to the chair structure.

The QST3 method

The QST3 method involved the input of a guess transition structure in addition to the reactant and product molecules and provided a more reliable method of obtaining the boat transition state. The anti2 conformers of 1,5-hexadiene, used initially in the QST2 method, were now used without modification because the orientation of the components in the transition state was predefined in the input file. The optimized allyl fragments were again used to construct a guess transition structure.

The first run of the QST3 method with the guess transition state as the second molecule group in the input file was observed to fail, producing a somewhat twisted boat transition structure. However, a second run with the the guess transition state as the third molecule group was successful in locating the boat structure, affording almost identical data to the QST2 method.

Modelling the Pathway from the Transition State to 1,5-Hexadiene Using the IRC Method

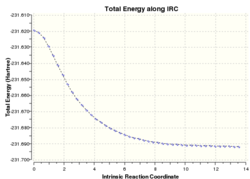
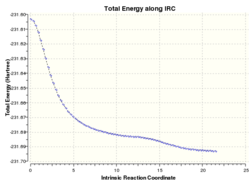
The intrinsic reaction coordinate (IRC) method can be used to simulate the lowest energy pathway from the transition state to the reactant or product molecule. The result of this calculation would then allow one to predict which conformers different transition state structures arise from. Chair and boat transition structures optimized in the previous section were used as the starting point for the IRC calculation and the general method is the same for both. The input file was specified to run in only the forward direction and to calculate the force constants at each data point for a maximum of 50 points. Again, the level of theory used was HF/3-21G. Table 1.4 summarizes the results from the IRC calculations.

Table 1.4 Results from the IRC calculations using HF/3-21G theory

Transition Conformation	Number of points to reach minimum	Local Minimum		Optimized Minimum		Conformer
		Structure	Energy (hartrees)	Structure	Energy (hartrees)
Chair (initial force constant)	44		-231.69157903		-231.69166702	gauche2
Boat (QST3)	75		-231.69261116		-231.69266119	gauche3

Starting from the chair transition state

The chair transition state optimized using the initial force constant method was used for this IRC calculation. The simulation ran for 44 points before a local energy minimum was located. The structure at this point was then visualized in Gaussview and its energy noted. The energy did not match exactly with any conformer in the appendix, though was closest to that of the gauche4 conformer. The local minimum was then re-optimized using HF/3-21G theory, resulting in the gauche2 conformer being obtained. It can be seen from the images in table 1.4 that the conformation of gauche2 is very similar to that of data point 44. Therefore, although gauche4 was closer in energy to the local minimum, it is likely that less structural rearrangement was required to obtain gauche2, leading to it being favoured in the optimization.

Starting from the boat transition state

Initially, the QST2 optimized boat transition structure was used as the starting point for the IRC calculation. This resulted in a local minimum being found after 45 points, however, the structure obtained for point 45 was the same as the input structure in the QST2 calculation - namely 1,5-hexadiene with modified dihedral and bond angles. In addition, this structure did not change upon further optimization. Nevertheless, it was found that using the output from the QST3 calculation did not have this problem and hence yielded more useful results. For this run, a local minimum was not found after 50 data points and another run was carried out with a maximum of 100 points. This time a local minimum was located after 75 points, with the structure at point 75 having very similar energy to the gauche3 conformer. Upon further optimization using the HF/3-21G level of theory, the gauche3 conformation was obtained as expected from both energy and structural considerations.

Re-optimization of the Transition Structures using B3LYP/6-31G* Theory

The chair and boat transition structures were re-optimized using the B3LYP/6-31G* level of theory. The same chair and boat transition structures as used for the IRC calculations were used in these optimization and frequency calculations. A summary of the key data is shown in table 1.5.

Upon comparison with the transition structures optimized at the HF/3-21G level of theory, it is clear there has been little change in the overall geometries of the chair and boat structures. However, one significant difference was in the distance between the allyl fragments. For the chair conformation, the distance was found to decrease for the higher level of theory, whereas for the boat conformation the distance increased. One possible reason for this is that steric interactions between the eclipsing allyl groups in the boat conformation are a more dominant factor in the B3LYP/6-31G* method than for HF/3-21G theory. Another more convincing reason is that the B3LYP/6-31G* level of theory takes into account the aromaticity of the chair conformation and non-aromatic nature of the boat conformation, thus resulting in the respective shortening and lengthening of the fragment distances. A comparison of the energies of the transition structures at the the two levels of theory shows the B3LYP/6-31G* method results significantly lower energies. This is not surprising as the two methods use different basis sets and hence a direct comparison here is not possible.

Table 1.5 Optimizing the chair and boat transition structures for the Cope rearrangement using B3LYP/6-31G* theory

Transition Conformation	Structure	Distance between terminal allyl carbons (angstroms)	Imaginary Frequency (cm-1)	Electronic Energy (hartrees)	Sum of Electronic and Zero Point Energies (hartrees)	Sum of Electronic and Thermal Energies (hartrees)
Chair (initial force constant)		1.968	-565.65	-234.55698287	-234.414932	-234.409011
Boat (QST3)		2.206	-531.04	-234.54309312	-234.402343	-234.396011

Calculation of the Activation Energies

Using the data obtained for the reactant (anti2) and the chair and boat transition states the activation energies can be calculated at both the HF/3-21G and B3LYP/6-31G* levels of the theory. In addition, using data found in the thermochemistry section of the log file, the activation energies at T = 0 K and T = 298 K can be found. Table 1.6 summaries the calculated activation energies and also includes experimentally determined values for comparison.

Upon heating of the system from T = 0 K to T = 298 K the activation energy for both the chair and boat pathways decreases. This is most likely because the reactant has a greater number of accessible vibrational modes than the transition state, leading to a greater increase of its potential energy upon heating. It can also be seen from the data that B3LYP/6-31G* theory provides energies much closer to the experimental data than HF/3-21G theory. This is of course expected from a higher level of theory and hence agrees with the expected outcome.

Table 1.6 Comparison of the computed and experimental activation energies at T = 0 and 298 K (in kcal/mol)

	HF/3-21G		B3LYP/6-31G*		Experimental
	T = 0 K	T = 298 K	T = 0 K	T = 298 K	T = 0 K
ΔE (chair)	45.710	44.696	34.056	31.161	33.5 ± 0.5
ΔE (boat)	55.604	54.760	41.956	41.319	44.7 ± 2.0

The Diels-Alder Cycloaddition

Introduction

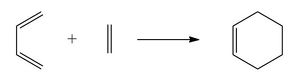
The Diels-Alder reaction is a [4+2] cycloaddition that occurs in a concerted fashion via an aromatic transition state. Six π electrons are involved in this reaction and hence it is allowed thermally with all suprafacial components according to the Woodward-Hoffmann selection rules. Typically the four electron component is an electron-rich diene and the two electron component (the "dienophile") is an electron-deficient alkene. In this case, the HOMO of the diene and the LUMO of the dienophile are close in energy, resulting in a low energy transition state. On the other hand, so-called hetero-Diels-Alder reactions involving electron poor hetero-dienes or 1,3-dipoles have the reverse situation in terms of frontier orbitals and are described as having inverse electron demand. Diels-Alder reactions are often kinetically controlled and the fastest formed product predominates.

The Cycloaddition of Butadiene and Ethylene

Butadiene reacts with ethylene in a cycloaddition reaction to form cyclohexene. The reaction is the simplest case of a [4+2] cycloaddition and regioselectivity is not an issue here. Computational studies have confirmed the concerted nature of this reaction at various levels of theory, with the concerted transition state being calculated as 7.7 kcal/mol lower in free energy than the lowest energy stepwise transition state.

Optimization of s-cis butadiene

s-cis Butadiene was optimized using the semi-empirical AM1 method. The resulting structure was planar and hence had a dihedral angle of 0^o. Table 2.1 below also includes the optimized structures using higher levels of theory. For both HF/3-21G and B3LYP/6-31G* methods steric repulsions dominated and consequently twisted gauche structures with reduced π-overlap were obtained.

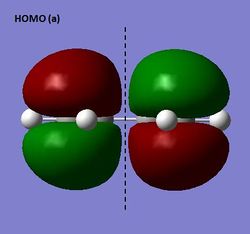
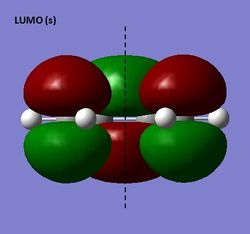
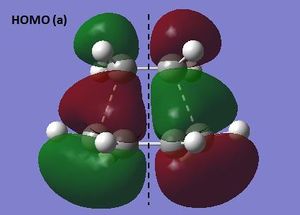
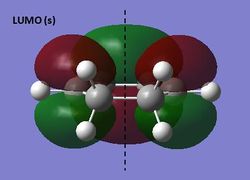
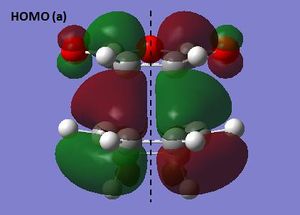
The HOMO and LUMO were visualized for the s-cis butadiene structure optimized using semi-emprical AM1 theory. The HOMO is antisymmetric (a) and the LUMO symmetric (s) with respect to the plane indicated.

Table 2.1 Summary of the structure and energies (in hartrees) of s-cis butadiene obtained from optimization calculations

Level of Theory	Structure	Dihedral angle (degrees)	Point Group	Electronic Energy	Sum of Electronic and Zero-point Energies	Sum of Electronic and Thermal Energies
Semi-empirical AM1		0.0	C2v	0.04879719	0.134553	0.138574
HF/3-21G		38.1	C2	-154.05513989	-153.963180	-153.958757
B3LYP/6-31G*		30.3	C2	-155.98648969	-155.901143	-155.896438

HOMO and LUMO of s-cis butadiene (semi-empirical AM1)

Optimization of ethene

The structure of ethene was optimized using three levels of theory, as for s-cis butadiene. The general structure remained planar for all methods, however the length of the C=C bond was observed to differ slightly in each case. The trend was not continuous with the increasing level of theory though, as the length of the C=C bond decreased in the HF/3-21G method but increased in the B3LYP/6-31G* method.

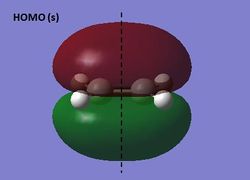
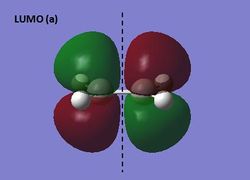
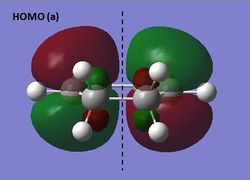
The HOMO and LUMO of ethene were visualized at the semi-empirical AM1 level of theory. It can be seen from the diagrams below that the HOMO is symmetric and the LUMO antisymmetric with respect to the plane.

Table 2.2 Summary of the structure and energies (in hartrees) of ethene obtained from optimization calculations

Level of Theory	General Structure	C=C bond length (Å)	Point Group	Electronic Energy	Sum of Electronic and Zero-point Energies	Sum of Electronic and Thermal Energies
Semi-empirical AM1		1.326	D2h	0.02619027	0.077198	0.080252
HF/3-21G		1.315	D2h	-77.60098736	-77.545896	-77.542938
B3LYP/6-31G*		1.331	D2h	-78.58745822	-78.536231	-78.533189

HOMO and LUMO of ethene

Optimization of the transition state

The transition state of the Diels-Alder cycloaddition was modelled initially at the semi-emprical AM1 level before using two higher levels of theory to obtain more accurate structures. The biocyclo[2.2.2]octane fragment was used in Gaussview to construct the guess transition state geometry. The bridging ethylene group was removed and the bond types changed to correspond to the cycloaddition reaction. The two fragments were assumed to be separated by 2.2 Å. The frozen coordinate method was then used to optimize the structure with the same procedure as used previously for the chair transition state of the Cope rearrangement. The structure obtained for the transition state at the semi-empirical AM1 level is shown below, along with the calculated HOMO and LUMO.

Optimized Structure, HOMO and LUMO of the transition state (semi-empirical AM1)

Inspection of the transition state HOMO indicates that the HOMO of cis butadiene interacts with the LUMO of ethene. Both of these MOs are antisymmetric and hence the HOMO of the transition state is also antisymmetric. On the other hand the LUMO of the transition state is symmetric with respect to the plane. The reaction is allowed because there is a strong HOMO/LUMO interaction as a result of a small energy gap between the interacting orbitals of the reactant as well as a significant overlap of electron density. The lengths of the partially formed σ-bonds in the transition state are identical and measure 2.120 Å. The average lengths of a C-C single bond and C=C double bond are 1.54 Å and 1.34 Å respectively. The van der Waals radius of a carbon atom however is 1.70 Å. The partially formed σ-bonds are much longer than an average C-C single bond but shorter than the van der Waals radii of two carbon atoms. Hence there is a small overlap of electron density and this corresponds to a bonding interaction rather than a formal C-C bond. On the other hand the length of the partially formed π-bond in the transition state lies between that of an average C-C single and double bond as expected.

The frequency calculation of the optimized transition state indicated a single imaginary frequency at -955.87 cm^-1, confirming that the transition state had been successfully located. Animation of this frequency showed the formation of the two σ-bonds to be synchronous. However the two lowest positive frequencies at 147.16 and 246.80 cm^-1 involved twisting of the ethylene fragment and asymmetric stretching of the partially formed σ-bonds respectively. This does not suggest the bond forming process is asynchronous though as these frequencies are positive and hence do not correspond to the nature of the forward reaction, rather the transition state itself.

The three levels of theory generated vastly different energies and imaginary frequencies as seen previously. The overall geometry of the transition structures however was similar, with a small increase in the lengths of the partially formed σ- and π-bonds being observed for the higher levels of theory.

Table 2.3 Summary of the structure and energies (in hartrees) of the Diels-Alder transition states

Level of Theory	General Structure	Length of partially formed σ-bonds (Å)	Length of partially formed π-bond (Å)	Imaginary Frequency (cm-1)	Electronic Energy	Sum of Electronic and Zero-point Energies	Sum of Electronic and Thermal Energies
Semi-empirical AM1		2.120	1.398	-955.87	0.11165482	0.253273	0.259449
HF/3-21G		2.210	1.394	-818.37	-231.60320833	-231.451338	-231.445651
B3LYP/6-31G*		2.272	1.407	-524.94	-234.54389651	-234.403323	-234.396906

Calculation of activation energies

The activation energies at T = 0 K and T = 298 K were calculated at three levels of theory based on data summarized in the previous three tables. Again, as was seen for the Cope rearrangement, the activation energies decreased upon increasing the temperature of the system. As noted for ethene, the trend here is also not continuous with respect to the level of theory used. In fact, the highest level of theory (B3LYP/6-31G*) gave the lowest activation energies. Furthermore, the lowest level of theory (semi-empirical AM1) gave energies closest to the experimental value. It is not clear why this is the case, as higher levels of theory should match the experimental data more closely. Hence it is more likely that the experimental value is incorrect, given that it was extrapolated from energies measured at much higher temperatures.

Table 2.4 Comparison of the computed and experimental activation energies at T = 0 and 298 K (in kcal/mol)

	semi-empirical AM1		HF/3-21G		B3LYP/6-31G*		Experimental
	T = 0 K	T = 298 K	T = 0 K	T = 298 K	T = 0 K	T = 298 K	T = 0 K
ΔE	26.055	25.491	36.231	35.168	21.367	20.533	25.1

The Cycloaddition of Cyclohexa-1,3-diene and Maleic Anhydride

The reaction between cyclohexa-1,3-diene and maleic anhydride is a more complex example of a Diels-Alder cycloaddition. Both components are substituted and consequently two stereoisomeric products are possible depending on whether the top or bottom face of maleic anhydride is attacked. For kinetically controlled reactions, the endo isomer is often favoured due to the presence of secondary orbital interactions that form in the transition state. A computational study of an analogous reaction involving maleic anhydride and cyclopentadiene found that the endo transition state is 1.01 kcal/mol lower in energy than the exo transition state and hence confirms that secondary interactions dominate over steric effects for this system. It is expected that the reaction under investigation will give similar results, though it is likely that the more bulky diene will lead to higher energy transition structures being obtained.

Optimization of cyclohexa-1,3-diene

The structure of cyclohexa-1,3-diene was optimized at two levels of theory. Optimization using the semi-empirical AM1 method gave a planar structure with C2 symmetry. This structure suffers from torsional strain at the sp³ carbon atoms due to eclipsing interactions between the hydrogen atoms. As a result, it is clear this structure is not an energy minimum and this is confirmed by the presence of a negative frequency in its IR spectrum at -73.97 cm^-1. This frequency represents a twisting motion of the ethylene fragment, which results in a lower energy conformation due to relief of torsional strain. It can be seen that the higher level of theory (HF/3-21G) accounts for this and thus gives a twisted structure with a gauche alignment of the sp³ carbons.

The HOMO and LUMO orbitals were visualized using semi-empirical AM1 theory, with the HOMO being antisymmetric and the LUMO symmetric with respect to the plane.

Table 2.5 Summary of the structure and energies (in hartrees) of cyclohexa-1,3-diene obtained from optimization calculations

Level of Theory	Structure	Dihedral angle (degrees)	Point Group	Electronic Energy	Sum of Electronic and Zero-point Energies	Sum of Electronic and Thermal Energies
Semi-empirical AM1		0.0	C2	0.02795781	0.152537	0.157031
HF/3-21G		44.1	C2	-230.54323124	-230.411186	-230.406354

HOMO and LUMO of cyclohexa-1,3-diene (semi-empirical AM1)

Optimization of maleic anhydride

Maleic anhydride was also optimized at two levels of theory, both of which generated planar structures with C_2v symmetry. Unlike for cyclohexa-1,3-diene, the optimized structure using semi-empirical AM1 theory for maleic anhydride is an energy minimum and hence no negative frequencies were observed in its IR spectrum.

The HOMO and LUMO of maleic anhydride at the semi-empirical AM1 level are shown below, with the HOMO being symmetric and the LUMO antisymmetric with respect to the plane. This is complementary to the case of cyclohexa-1,3-diene and thus allows for good overlap between the frontier orbitals of the reactants in the transition state.

Table 2.6 Summary of the structure and energies (in hartrees) of maleic anhydride obtained from optimization calculations

Level of Theory	General Structure	Point Group	Electronic Energy	Sum of Electronic and Zero-point Energies	Sum of Electronic and Thermal Energies
Semi-empirical AM1		C2v	-0.12182383	-0.063347	-0.058193
HF/3-21G		C2v	-375.10351351	-375.042901	-375.038068

HOMO and LUMO of maleic anhydride

Optimization of the transition states

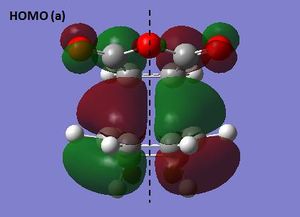
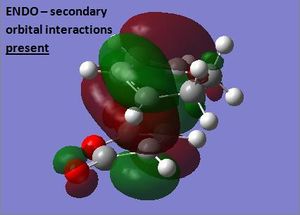
The transition structures for the exo and endo transition states were calculated using the frozen coordinate method, as for the previous cycloaddition reaction. For this reaction only two levels of theory were used. The B3LYP/6-31G* method used previously was found to be a lengthy calculation for this system and hence was not carried out due to time constraints. The initial guess structure for both transition states was again constructed using the bicyclooctane fragment as a starting point, with the distance between the two components being 2.2 Å. The optimized structures and HOMOs of the exo and endo transition structures at the semi-empirical AM1 level are shown below. Table 2.7 summarizes the structures and energies obtained from the optimization and frequency calculations. For each transition structure, one observed imaginary frequency was obtained. The distance between the -(C=O)-O-(C=O)- group of maleic anhydride and the group opposite on the diene was measured as the shortest distance between two atoms on different components. For the exo structure this was between a hydrogen on the bridging ethylene group and the carbonyl carbon and for the endo structure was between a carbon in the -CH=CH- group and the carbonyl carbon.

Optimized Structure and HOMO of the exo transition state (semi-empirical AM1)

Optimized Structure and HOMO of the endo transition state (semi-empirical AM1)

There are a number of similarities between the optimized structures of the exo and endo transition states. For example, they both have C_S symmetry and their HOMOs both involve the LUMO of maleic anhydride and the HOMO of cyclohexa-1,3-diene and hence are antisymmetric. There is good overlap between the π systems in both cases and hence this confirms the reaction is allowed thermally.

The two levels of theory again gave transition structures with similar overall structures, but with differences in the lengths of the partially formed bonds. The higher level of theory (HF/3-21G) led to increases in the length of the partially formed σ-bonds and decreases in the length of the partially formed π-bond, suggesting the transition state is earlier along the reaction coordinate for HF/3-21G theory. Overall, however, the distance between the fragments were found to be relatively similar for the exo and endo transition structures, indicating there is an optimum distance for orbital overlap. Consequently, this was observed to result in shorter distances between the -(C=O)-O-(C=O)- group of maleic anhydride and the group opposite in the exo structure, leading to a more crowded environment than in the endo structure. This suggests the exo form is more strained and thus is expected to be higher in energy. Another factor which adds to this energy difference is the presence of secondary orbital interactions in the endo structure. The MO of the -(C=O)-O-(C=O)- fragment is antisymmetric with respect to the plane indicated and hence has the correct symmetry to overlap with the π system of the opposite -CH=CH- group. This interaction acts to stabilise the transition state and therefore lowers its overall energy. On the other hand, the exo structure cannot form secondary interactions as the -(C=O)-O-(C=O)- group is too far away in space to effectively overlap with the orbitals of the diene. At the semi-emprical AM1 level the exo structure is calculated to be 0.681 kcal/mol higher in energy, and for the HF/3-21G level is 4.253 kcal/mol higher in energy. This result indicates that the secondary orbital interactions are likely not to be included in the semi-emprical AM1 method, thus leading to the small observed energy difference.

Table 2.7 Summary of the structure and energies (in hartrees) of the exo and endo transition states obtained from optimization calculations

Transition Geometry	General Structure	Level of Theory	Length of partially formed σ-bonds (Å)	Length of partially formed π-bond (Å)	distance between -(C=O)-O-(C=O)- and opposite group (Å)	Imaginary Frequency (cm-1)	Electronic Energy	Sum of Electronic and Zero-point Energies	Sum of Electronic and Thermal Energies
Exo		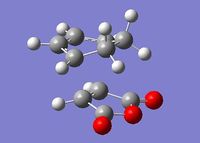Semi-empirical AM1	2.170	1.397	2.416	-812.19	-0.05041985	0.134881	0.144881
		HF/3-21G	2.261	1.340	2.426	-647.46	-605.60359125	-605.408139	-605.398679
Endo		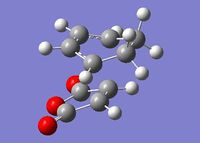Semi-empirical AM1	2.162	1.397	2.892	-806.42	-0.05150480	0.133494	0.143683
		HF/3-21G	2.231	1.396	2.847	-643.79	-605.61036821	-605.414902	-605.405476

Calculation of activation energies

The activation energies have been calculated for two levels of theory based on data from previous optimization and frequency calculations. It is clear that for both levels of theory, the activation energy is lower for the endo pathway than for the exo pathway, as predicted from the analysis of the computed structures and molecular orbitals. The energy difference between the exo and endo pathways is more pronounced at the HF/3-21G level as secondary interactions were found to not be accounted for in the semi-empirical AM1 method. One major difference in comparison to previous activation energy data is the temperature dependence. For this reaction, an increase in temperature was found to generally lead to an increase in activation energy, the opposite to what has been seen in previous reactions. In addition, there was a very large increase of 2.883 kcal/mol for the endo pathway using HF/3-21G theory. The reason for this temperature dependence is unclear and further studies at higher levels of theory should be undertaken to find out whether this trend continues.

Table 2.8 Summary of the activation energies (in kcal/mol)

	semi-empirical AM1		HF/3-21G
	T = 0 K	T = 298 K	T = 0 K	T = 298 K
ΔE (exo)	28.672	28.892	28.833	28.704
ΔE (endo)	27.801	28.141	21.556	24.439

What effects have been neglected in these calculations of Diels Alder transition states?

1) Solvent effects: The calculations carried out in this report were all in the gas-phase and therefore solvent effects were completely neglected. It has been observed experimentally that varying the solvent results in minimal changes in the rate of reaction, indicating that the difference in polarity between the transition state and reactants is relatively small for most systems. This is expected for cycloaddition reactions as their mechanisms usually involve concerted and synchronous bond formation. In particular, it would be interesting to see whether using water as the solvent has a significant effect, which has been found in the literature to accelerate pericyclic reactions by a factor of 10 to 100.

2) Pressure dependence: Cycloaddition reactions combine the ends of two conjugated π systems to form a single product molecule, therefore reducing the total volume of the system in the forward reaction. Consequently, the pressure dependence of cycloaddition reactions is often very strong. In addition, it has been noted that for the Diels-Alder reactions of maleic anhydride the volume of activation is significantly larger than the total change in volume, which suggests the transition state structures occupy smaller volumes than the products. This is a distinctive property of reactions involving maleic anhydride and is not common to cycloadditions in general. It would be interesting to see whether computational studies are able to predict this experimental behaviour.

3) Regioselectivity: Both Diels-Alder reactions under investigation involved reactants which were symmetric with respect to the plane. As a result, regioselectivity of the reactions did not need to be discussed. For unsymmetrical starting materials, regioselectivty must be considered in addition to stereoselctivity. The frontier orbitals of the reactants are analysed to determine which combination results in the greatest HOMO/LUMO overlap. For normal electron demand Diels-Alder reactions, 1-substitued dienes give mainly the ortho product and 2-substituted dienes give mainly the para product with singly substituted dienophiles.

4) Product stability - kinetic or thermodynamic control?: Calculating the product energies was not carried out in this computational investigation, and hence it was only assumed that the reactions were under kinetic control. Comparison of the product energies with experimental findings would provide direct confirmation of whether this assumption was valid. In kinetically controlled reactions the fastest formed product predominates whereas in thermodynamically controlled reactions the most stable product predominates.