Rep:Mod:Vishali Pala
Ammonia
jmol Image
An ammonia molecule optimised in GaussView |
The image above shows the trigonal pyramidal structure of ammonia, formed due to extra repulsion provided by the lone pair on nitrogen, distorting the molecule's structure from having a tetrahedral bond angle of 109.5°.
Summary of results from optimisation
| Parameter | Result | Literature Value |
|---|---|---|
| Molecular formula | NH3 | |
| Calculation method | RB3LYP | |
| Basis set | 6-31G(d.p) | |
| Final Energy E(RB3LYP) | -56.55776873 a.u. | |
| RMS gradient | 0.00000485 a.u. | |
| Point group | C3V | |
| Optimised N-H bond distance | 1.01798 angstroms | 1.008 angstroms [1] |
| Optimised H-N-H bond angle | 105.741° | 107.298° [1] |
There is good agreement between the values found in GaussView and literature values. Percentage errors on bond length and bond angle are 0.99% and 1.45% respectively. Slight variation can be accounted for by a possibility that optimisation was not fully complete.
Item table
| Item | Value | Threshold | Converged? |
|---|---|---|---|
| Maximum Force | 0.000004 | 0.000450 | YES |
| RMS Force | 0.000004 | 0.000300 | YES |
| Maximum Displacement | 0.000072 | 0.001800 | YES |
| RMS Displacement | 0.000035 | 0.001200 | YES |
Predicted change in Energy=-5.986271D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
The optimisation file is linked to here
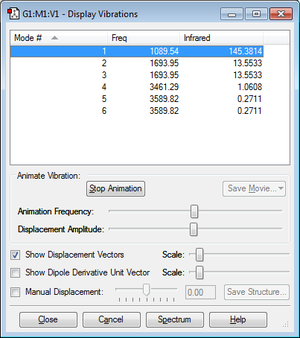
Summary of vibration results
| Parameter | Result |
|---|---|
| Number of modes expected from 3N-6 | 6 |
| Number of degenerate modes | (2 and 3) and (5 and 6) |
| Bending vibrations | 1, 2 and 3 |
| Bond stretch vibrations set | 4, 5 and 6 |
| Highly symmetric mode | 4 |
| Umbrella mode | 1 |
| Number of bands expected in experimental spectrum of gaseous ammonia | 4 |
| Charge on N atom | -1.125 a.u. |
| Charge on H atoms | 0.375 a.u. |
The degenerate modes have equivalent energies and therefore will appear as single peaks in the IR spectrum. As a result, 4 bands are expected in the experimental spectrum, despite there being 6 vibrational modes. Looking at the charge distribution, it is as expected in an ammonia molecule as nitrogen is much more electronegative than hydrogen. Therefore the N-H bond is polarized and a partial negative charge on nitrogen and a partial positive charge on hydrogen is observed.
Mode 1 has a much stronger absorbance in the IR spectrum than the other modes. This can be explained as this bending vibration creates a much greater change in dipole moment and therefore is more strongly detected.
Nitrogen
jmol Image
A nitrogen molecule optimised in GaussView |
The image above shows a linear nitrogen molecule, with a strong triple bond that contributes to the stability of the molecule, and explains why a much more lower energy is obtained compared to that of ammonia or hydrogen.
Summary of results from optimisation
| Parameter | Result | Literature Value |
|---|---|---|
| Molecular formula | N2 | |
| Calculation method | RB3LYP | |
| Basis set | 6-31G(d.p) | |
| Final Energy E(RB3LYP) | -109.52412868 a.u. | |
| RMS gradient | 0.00000060 a.u. | |
| Point group | Dinfh | |
| Optimised bond distance | 1.10550 angstroms | 1.0975 angstroms [2] |
Again, the predicted and literature values for the bond length are in strong agreement, giving a small percentage error of 0.73%
Item table
| Item | Value | Threshold | Converged? |
|---|---|---|---|
| Maximum Force | 0.000001 | 0.000450 | YES |
| RMS Force | 0.000001 | 0.000300 | YES |
| Maximum Displacement | 0.000000 | 0.001800 | YES |
| RMS Displacement | 0.000000 | 0.001200 | YES |
Predicted change in Energy=-3.401000D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
The optimisation file is linked to here
Summary of vibration results
There is no absorbance detected for the nitrogen molecule. This is because it is a diatomic homonuclear molecule and therefore there is no change in dipole moment during the vibration. As a result, it is IR inactive.
Hydrogen
jmol Image
A hydrogen molecule optimised in Gaussview |
Summary of results from optimisation
| Parameter | Result | Literature Value |
|---|---|---|
| Molecular formula | H2 | |
| Calculation method | RB3LYP | |
| Basis set | 6-31G(d.p) | |
| Final Energy E(RB3LYP) | -1.17853936 a.u. | |
| RMS gradient | 0.00000017 a.u. | |
| Point group | Dinfh | |
| Optimised bond distance | 0.74279 angstroms | 0.74 angstroms [3] |
This shows very strong agreement with the literature. Percentage error on the bond length is found to be 0.38%
Item table
| Item | Value | Threshold | Converged? |
|---|---|---|---|
| Maximum Force | 0.000000 | 0.000450 | YES |
| RMS Force | 0.000000 | 0.000300 | YES |
| Maximum Displacement | 0.000000 | 0.001800 | YES |
| RMS Displacement | 0.000001 | 0.001200 | YES |
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7428 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
The optimisation file is linked to here
Summary of vibration results
Similar to nitrogen, no absorbance is recorded for hydrogen. Again, this is a homonuclear diatomic molecule and so there is no change in dipole moment during the stretching vibration, making it IR inactive.
Haber-Bosch Process
The Haber-Bosch process is used industrially in the manufacture of ammonia. Understanding the reaction is essential for optimising conditions in order to increase reaction rates and maximise yield and therefore profit. Below is the overall forward reaction that takes place:
N2 + 3H2 → 2NH3
This exists in equilibrium with the reverse reaction which involves decomposition of ammonia into nitrogen and hydrogen gas. The forward reaction is exothermic and therefore favoured by lower temperatures according to Le Chatelier's principle. Furthermore, since 4 moles of reactant form 2 moles of product, the forward reaction is favoured by higher pressures. In reality, low temperatures decrease the rate of reaction and high pressures require expensive equipment that can withstand this and therefore compromising conditions are used.
Using the energy values calculated previously for ammonia, nitrogen and hydrogen, it is possible to find the energy change for the reaction, as has been done step by step below:
| E(NH3) | -56.55776873 a.u. |
| 2E(NH3) | -113.11553746 a.u. |
| E(N2) | -109.52412868 a.u. |
| E(H2) | -1.17853936 a.u. |
| 3E(H2) | -3.53561808 a.u. |
| ΔE=2*E(NH3)-[E(N2)+3*E(H2)] | -0.0557907 a.u. |
Therefore the energy change for this reaction is -146.48 kJ mol-1. The Gibbs Free energy change is negative and therefore the product (ammonia) is more stable than the reactant gases.
Tetrahydroborate ion
jmol Image
A tetrahydroborate ion optimised in GaussView |
The image above shows the tetrahedral structure of the tetrahydroborate ion. Boron is electron deficient and therefore acts as a lewis acid, accepting an electron pair to form a dative covalent bond with hydrogen. This allows it to complete its octet.
Summary of results from optimisation
| Parameter | Result | Literature Value |
|---|---|---|
| Molecular formula | BH4- | |
| Calculation method | RB3LYP | |
| Basis set | 6-31G(d.p) | |
| Final Energy E(RB3LYP) | -27.24992681 a.u. | |
| RMS gradient | 0.00003029 a.u. | |
| Point group | C1 | |
| Optimised B-H bond distance | 1.23944 angstroms | 1.19 angstroms [4] |
| Optimised H-B-H bond angle | 109.476° |
Percentage error on the bond length is 4.15%.
Item table
| Item | Value | Threshold | Converged? |
|---|---|---|---|
| Maximum Force | 0.000047 | 0.000450 | YES |
| RMS Force | 0.000030 | 0.000300 | YES |
| Maximum Displacement | 0.000823 | 0.001800 | YES |
| RMS Displacement | 0.000378 | 0.001200 | YES |
Predicted change in Energy=-6.978471D-08
Optimization completed.
Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.2393 -DE/DX = 0.0 !
! R2 R(1,3) 1.2393 -DE/DX = 0.0 !
! R3 R(1,4) 1.2395 -DE/DX = 0.0 !
! R4 R(1,5) 1.2394 -DE/DX = 0.0 !
! A1 A(2,1,3) 109.4358 -DE/DX = 0.0 !
! A2 A(2,1,4) 109.5147 -DE/DX = 0.0 !
! A3 A(2,1,5) 109.4762 -DE/DX = 0.0 !
! A4 A(3,1,4) 109.4695 -DE/DX = 0.0 !
! A5 A(3,1,5) 109.4765 -DE/DX = 0.0 !
! A6 A(4,1,5) 109.4546 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -119.9822 -DE/DX = 0.0 !
! D2 D(2,1,5,3) 119.9629 -DE/DX = 0.0 !
! D3 D(2,1,5,4) -120.0461 -DE/DX = 0.0 !
! D4 D(3,1,5,4) 119.991 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
The optimisation file is linked to here
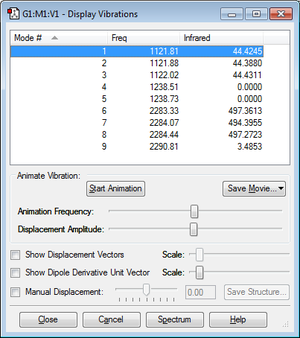
Summary of vibration results
| Parameter | Result |
|---|---|
| Number of modes expected from 3N-6 | 9 |
| Number of degenerate modes | (1, 2 and 3) and (4 and 5) and (6,7,8) |
| Bending vibrations | 1, 2, 3, 4 and 5 |
| Bond stretch vibrations | 6, 7, 8 and 9 |
| Charge on B atom | -0.615 |
| Charge on H atoms | -0.096 |
Modes 4 and 5 show no absorbance at the relevant frequency. This is due to the vibration causing no change in dipole moment overall. Modes 6, 7 and 8 are more strongly detected in the IR spectrum prediction as they involve a stronger change in dipole moment. Comparing the electronegativities of boron and hydrogen, which are 2.04[5] and 2.2[6]respectively, there is not a large difference, and hydrogen is in fact more electronegative. Despite this, boron has a larger partial negative charge which can be explained as it makes a dative covalent bond with hydrogen, giving it a noble gas configuration and therefore more electron density surrounds the central boron atom.
Molecular Orbitals
| 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|
 |
 |
 |
 |
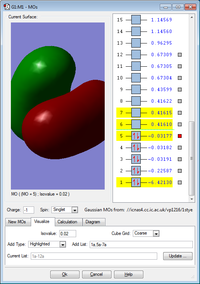 |
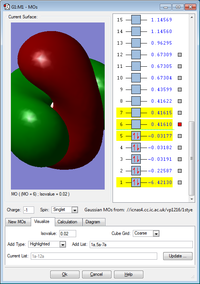 |
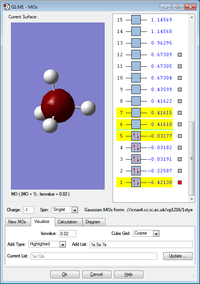
MO no. 1 is a visual representation of the deepest energy molecular orbital. There is no overlap between the atoms and therefore it is a non bonding MO, consisting of only the 1s atomic orbital on boron. It is occupied, but the 1s electrons are core and therefore not involved in bonding.
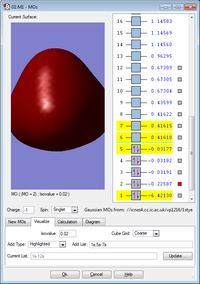
MO no. 2 is formed from the overlap between the 2s atomic orbital on boron and the 1s atomic orbital on hydrogen to form a sigma bond. This MO is occupied and involved in bonding as the electrons in 2s on boron are valence.
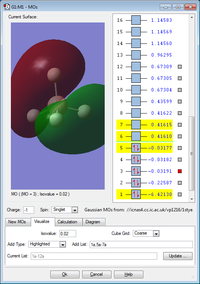
MO's no. 3, 4 and 5 are all degenerate and formed by the overlap of 3 x 2p atomic orbtials on boron and the 1s atomic orbital on hydrogen. This forms 1 sigma bond and 2 pi bonds. MO 5 is the highest occupied molecular orbital (HOMO).
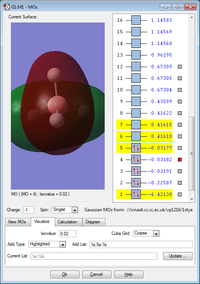
MO 6 is the lowest unoccupied molecular orbital (LUMO). The energy difference of 0.38433 a.u. represents the energy required to make the HOMO-LUMO transition.
References
- ↑ 1.0 1.1 http://www.kayelaby.npl.co.uk/chemistry/3_7/3_7_3.html.
- ↑ http://www.wiredchemist.com/chemistry/data/nitrogen-compounds.
- ↑ http://www.wiredchemist.com/chemistry/data/bond_energies_lengths.html.
- ↑ http://www.wiredchemist.com/chemistry/data/bond_energies_lengths.html.
- ↑ https://www.webelements.com/hydrogen/electronegativity.html.
- ↑ https://www.webelements.com/boron/electronegativity.html.