Rep:Mod:VilfyPhys
Endo final product |
to view the surfaces you have to look at .chk file.
Computational Module 3 (Physical)
This computational experiment introduces and analyses examples of two pericyclic reaction types - the Cope rearrangement, discovered by A. Cope [1] and the Diels Alder cycloaddition discovered by O. Diels and K. Alder[2]. The two reactions were investigated by carrying out computational chemistry calculations, whereby generally speaking, respective structures were optimised, transition states were both calculated and analysed and other analysis and interpretation of the data was performed, as outlined in the following.
The Cope Rearrangement Tutorial
Introduction
The Cope rearrangement belongs to the category of pericyclic reactions, meaning that a cyclic transition state is present for molecules that undergo this rearrangement route. In the process of a [3,3]-sigmatropic shift an allyl group migrates. This migration occurs with a concerted bond formation and breakage at different sides of the molecule. The example below shows the intramolecular rearrangement of a 1,5 diene triggered by heat.
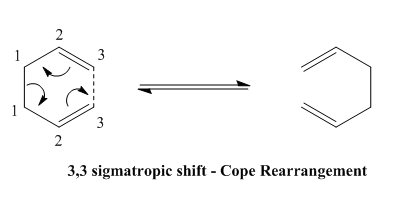
This Cope rearrangement involves the movement of 6 electrons (4n+2). The reaction is thermally allowed via Hückel Topology, bearing suprafacial components (as opposed to antarafacial which would have been the case for a photochemically triggered reaction). The rearrangement can undergo two different types of transition states, the boat or the chair (see below), whereby the chair is considered to be lower in energy due to less steric repulsions.
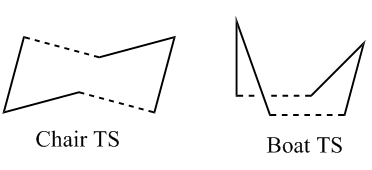
The Cope rearrangement stands in equilibrium, however the addition of substituents to the 1,5-hexadiene at the 3 or 4 position i.e. where the bond breakage or formation would take place, changes this and favours certain rearrangement to others. A more substituted end product would be favoured in that case due to increased thermodynamic stability at the more substituted end.
The following exercises demonstrate how the different transition states of 1,5-hexadiene can be analysed by investigating respective activation energies of the rearrangements and energy differences of varioous transition states to predict reactivity. Furthermore, symmetry was considered to correctly confirm the optimised structures, and energy pathways were calculated to identify local energy minima.
The Optimisation of the Reactants and Products
This part looks at different conformers (anti and gauche) of 1,5-hexadiene and optimises their structures, finds transition states and characterises their symmetry by finding their corresponding point groups. The following calculations also investigate vibrational frequencies to identifiy and reconfirm whether an optimisation or transition state was calculated. As a general procedure for the following exercises, all structures were created on the Gausview software, thereafter cleaned and optimised using the Hessian method which can be either HF/3-21G i.e. Hartree-Fock or B3LYP/6-31G(d) i.e. DFT. The (label) refers to the label found in the script to prove and show which structure the calculated molecule corresponds to.
1,5-hexadiene anti-periplanar conformer (anti1)
1,5-hexadiene was created in Gaussview in its antiperiplanar form, meaning that the dihedral angle was set at 180º between the four central Carbon atoms. The molecule was cleaned and optimised via the HF/3-21G method. The molecular structure can be found below.
Anti conformer |
Below is a summary of the obtained data on the molecule.
| Category | Result |
|---|---|
| File Type | .chk |
| Calculation Type | FOPT |
| Calculation Method | RHF |
| Basis Set | 3-21G |
| Charge | 0 |
| Spin | Singlet |
| Total Energy (a.u.) | -231.69260235 |
| Total Energy (kcal/mol) | -145,389.33408424 |
| RMS Gradient Norm | 0.00001824 a.u. |
| Dipole Moment | 0.2021 Debye |
| Point Group | C2 |
| Log File | File:2 ANTI.LOG |
1,5-hexadiene gauche conformer (gauche4)
1,5-hexadiene was created in Gaussview in its gauche form, meaning that this time the dihedral angle was set at 60º instead of 180º between the four central Carbon atoms. The optimisation energy was expected be higher than for the previous case due to larger steric interactions in the gauche form. The molecule was cleaned and optimised via the HF/3-21G method. The molecular structure can be found below.
Gauche conformer |
| Category | Result |
|---|---|
| File Type | .chk |
| Calculation Type | FOPT |
| Calculation Method | RHF |
| Basis Set | 3-21G |
| Charge | 0 |
| Spin | Singlet |
| Total Energy (a.u.) | -231.69153032 |
| Total Energy (kcal/mol) | -145,388.66137511 |
| RMS Gradient Norm | 0.00002038 a.u. |
| Dipole Moment | 0.1281 Debye |
| Point Group | C2 |
| Log File | File:4 GAUCHE.LOG |
As predicted, the anti-structure turned out to be lower in energy which was assumed to be, due to steric effects. The gauche conformation pushes the four central atoms of the six membered Carbon chain to a close structure, whereby steric repulsion can occur.
Finding and rationalising the lowest energy conformer
Gauche 3 is lowest in energy. The fact that it is a gauche structure shows that steric effects do not play the crucial role but stereoelectronics are even more relevant when about reducing the energy of the molecule to a minimum. This instance is due to the gauche effect. The effect is particularly strong for the gauche 3 conformer (refer to appendix 1 in script) as electron donation from the C=C bond (π-bond) can be very well transferred to the σ* C-H, due to the geometry the molecule is in i.e. 60º. This process is also known as sigma conjugation. A good overlap of the bonding and anti-bonding orbitals is achieved as shown in the figure below which gives rise to an increased stabilisation for this orientation of this molecular structure.
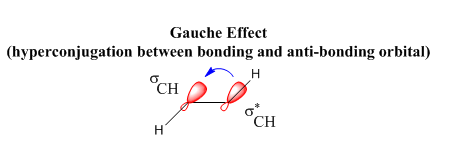
The gauche 3 conformer was therefore constructed on ‘‘Gaussview‘‘, cleaned and optimised via the HF/3-21G method. The molecular structure, as well as a summary of the energy values obtained is shown below.
1,5-hexadiene (gauche) conformer (gauche 3)
Gauche 3 conformer |
| Category | Result |
|---|---|
| File Type | .chk |
| Calculation Type | FOPT |
| Calculation Method | RHF |
| Basis Set | 3-21G |
| Charge | 0 |
| Spin | Singlet |
| Total Energy (a.u.) | -231.69266122 |
| Total Energy (kcal/mol) | -145389.37102573 |
| RMS Gradient Norm | 0.00000927 a.u. |
| Dipole Moment | 0.3407 Debye |
| Point Group | C1 |
| Log File | File:3 GAUCHE.LOG |
1,5-hexadiene anti conformer (Cianti2)
This exercise investigated the anti2 conformer. First, the structure was drawn out in Gausview, cleaned and optimised via the HF/3-21G method.
1,5-hexadiene Cianti2 conformer (HF/3-21G)
Anti 2 conformer |
Below is the summary of the significant data for this calculation:
| Category | Result |
|---|---|
| File Type | .chk |
| Calculation Type | FOPT |
| Calculation Method | RHF |
| Basis Set | 3-21G |
| Charge | 0 |
| Spin | Singlet |
| Total Energy (a.u.) | -231.69253528 |
| Total Energy (kcal/mol) | -145389.29199717 |
| RMS Gradient Norm | 0.00001891 a.u. |
| Dipole Moment | 0.0000 Debye |
| Point Group | Ci |
| Log File | File:C(I) ANTI2.LOG |
The Hessian method can be carried out in two different methods, the lower level one (HF/3-21G) and the higher level one (B3LYP/6-31G(d)). The lower level method, as will be shown later on is very useful to get an idea of whether a calculation was set up correctly, as it usually runs faster. The Hartree-Fock method is also more useful to analyse the orbitals of the optimised product or the transition state. The higher level method (also known as DFT) is more accurate when calculating energies, it runs longer, uses less to almost no assumptions in the energy calculation and usually gives better results, as opposed to the Hartree Fock method. The second step in the analysis of the 1,5-hexadiene Cianti2 conformer was about the reoptimisation of the output file of the HF/3-21G calculation in Gaussview by applying the DFT method.
1,5-hexadiene Cianti2 conformer (B3LYP/6-31G(d))
C(i) anti2 DFT calculation |
| Category | Result |
|---|---|
| File Type | .chk |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(D) |
| Charge | 0 |
| Spin | Singlet |
| Total Energy (a.u.) | -234.61170280 |
| Total Energy (kcal/mol) | -145,338.56883933 |
| RMS Gradient Norm | 0.00001326 a.u. |
| Dipole Moment | 0.0000 Debye |
| Point Group | Ci |
| Log File | File:C(I) ANTI2 DFT RECALCULATION.LOG |
Due to a change in basis sets between the two methods, a comparison of respective energies cannot be made. The two methods are based on different assumptions with respect to the theory they refer to and thus only the energies of molecules that were optimised by the same method can be compared. Nevertheless, it can be seen that the difference in bond lengths, especially at the C=C double bond is different for the two Hessian methods. The difference may be minimal, however it cannot be disregarded. Furthermore, the bond angles differ slightly between the two optmisation methods. The point group stays the same, so does therefore the symmetry of the molecule for both optimisations.
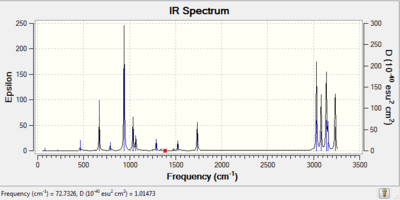
The last part in the analysis of the 1,5-hexadiene Cianti2 conformer was to investigate the frequencies. The key point was to show that no negative i.e. imaginary frequency was obtained in the optimisation calculation, hence proving a successful minimisation as opposed to a transition state calculation, where negative frequencies are present. Frequency calculations were run via the DFT method at both room temperature(File:C(I) ANTI2 FREQUENCY CALC.LOG) and at 0.001K(File:C(I) ANTI2 FREQUENCY CALC FOR 0K.LOG), giving the same IR spectra which is shown below.
The vibration data indicated 42 different vibrations that gave rise to the obtained IR spectrum. The highest frequency vibration of the in total 42 vibrations is shown below:
Furthermore, the thermochemistry data for these calculations was investigated and respective energies for the room temperature and 0K case were compared. The different energy contributions that were considered were sum of electronic and zero-point energies (=Epot at 0 K including the zero-point vibrational energy), sum of electronic and thermal energies (=E at 298K and 1 atm of pressure which includes contributions from the rotational, translational and vibrational energy modes at this temperature), sum of electronic and thermal enthalpies and sum of electronic and thermal free energies.
| Energy classification | Respective equation | Energy in a.u. (at 298K) | Energy in kcal/mol (298K) | Energy in a.u. at 0.001K |
|---|---|---|---|---|
| Sum of electronic and zero-point energies | E = Eelec + ZPE | -234.469212 | -147131.683317 | -234.469212 |
| Sum of electronic and thermal energies | E(298K) = E(0K) + Evib + Erot + Etrans | -234.461856 | -147127.067357 | -234.469212 |
| Sum of electronic and thermal enthalpies | H = E(298K) RT | -234.460912 | -147126.474988 | -234.469212 |
| Sum of electronic and thermal free energies | G = H -TS | -234.500821 | -147151.518269 | -234469212 |
0K could not be achieved, as Gaussview did not accept it as keyword, therefore temperature=0.001 was chosen. In the data of Table 6' it can be seen that the energies for the measurements at 0.0001K were all the same, for all different considered sums of energies. the obtained value -234.469212 is also equal to the energy obtained for the sum of electronic and zero-point energies which makes sense, since at 0K, the other energy sums do not play key role.
For all calculations carried out so far it must be kept mind that:
- No imaginary frequencies were observed for any of the calculations, meaning that optimisations were successfully calculated as opposed to transition states.
- The RMS gradient (shown in the summary tables) gave low values, indicating that minimum values were reached i.e. reconfirms a successful optimisation.
- All values obtained matched clearly with the values given in the Appendix in the script.
- The two Hessian methods DFT and Hartree-Fock cannot be compared in terms of their energy results.
Chair and Boat Optimisations
The next exercise investigates 3 different computational methods applied on the chair and boat structure of cyclohexane. The three considered methods are the Hessian method, the freeze coordinate = redundant coordinate method which consist of two steps and the QST2 method.
Hessian Method (chair)
The exercise was started by the optimisation of an allyl fragment (C3H5). The product of this optimisation process and the corresponding data is shown below:
| Category | Result |
|---|---|
| File Type | .chk |
| Calculation Type | FOPT |
| Calculation Method | UHF |
| Basis Set | 3-21G |
| Charge | 0 |
| Spin | Doublet |
| Total Energy (a.u.) | -115.8230401 |
| Total Energy (kcal/mol) | -72,680.07049406 |
| RMS Gradient Norm | 0.00003049 |
| Dipole Moment | 0.0292 Debye |
| Point Group | C1 |
| C-C-C bond angle | 124º |
| Equal bond distances | 1.39Å |
| Log File | File:C(I) ANTI2 DFT RECALCULATION.LOG |
Thereafter a guess chair structure was constructed made out of two allyl fragments which had to be moved manually to take in the correct geometry and the transition state was calculated. On Gaussview this was achieved by selecting Opt+Freq as job type, whereby the structure was set to be optimised to a TS (Berny) and the Force constant was calculated once. The method was HF/3-21G and the keyword that is usually used for transition state calculations is opt=noeigen.
An image of the guessed transition structure is given below, followed by an animation of the obtain transition state.
The above animation on the right (if it is not activated please click on it) was obtained by investigating the vibrations obtained in the output (LOG) file of the chair transition state calculation. A negative, imaginary frequency was observed at -818.01cm-1. The two C-C bond lengths that were pointed out in the guess chair structure were minimsed to be 2.20Å (File:Chair TransitionState Method 1.LOG). The table below reconfirms the formation of the correct transition state, also due to its great accuracy with the values in Appendix 2 in the script.
| Category | Result |
|---|---|
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RHF |
| Basis Set | 3-21G |
| Charge | 0 |
| Spin | Singlet |
| Total Energy (a.u.) | -231.6932230 |
| Total Energy (kcal/mol) | -145,389.7235481 |
| RMS Gradient Norm | 0.00004545 |
| Imaginary Frequency | -818.01 cm-1 |
| Dipole Moment | 0.0011 Debye |
| Point Group | C2h (after symmetrisation of the molecule) |
Finally the Thermochemistry data for the chair structure was found and is shown below:
| Energy classification | Respective equation | Energy in a.u. (at 298K) | Energy in kcal/mol (298K) |
|---|---|---|---|
| Sum of electronic and zero-point energies | E = Eelec + ZPE | -231.466696 | -145247.575679 |
| Sum of electronic and thermal energies | E(298K) = E(0K) + Evib + Erot + Etrans | -231.461338 | -145244.213483 |
| Sum of electronic and thermal enthalpies | H = E(298K) RT | -231.460393 | -145243.62049 |
| Sum of electronic and thermal free energies | G = H -TS | -231.495201 | -145265.46284 |
Freeze Coordinate Method (chair)
The second method that was investigated for the chair structure was the frozen coordinate method. This method is carried out in two steps. This method is different from the Hessian method in the sense that it does not calculate force constants. The frozen coordinate method rather differentiates along the reaction coordinate. This approach can turn out to be much quicker, especially when trying to optimise or calculate transition state structures, where the exact position of the atoms for the guess structure are far apart from the reality case. In this way, the unknown bond distances can be regarded as redundant at first, and once the structure has been correctly optimised, the distances can be calculated to obtain the final structure.
To carry out this method, the two allyl fragments were again matched up in the way to form a chair structure when combined. The first step was about selecting the distances between the terminal Carbon atoms as redundant coordinates and the structure was optimised. It was found that after this first optimisation, the bond distances between the terminal Carbon atoms were fixed at 2.2Å. In the second part another optimisation was run, whereby the previously fixed bond distances were relaxed to allow for the correct chair transition state to form. The keyword used in step 1 was Opt=ModRedundant. The final distances between the terminal Carbon atoms were again 2.02 Å. The transition state obtained was almost identical with the one obtained via the Hessian method. All results obtained are listed below.
| Category | Result |
|---|---|
| File Type | .log |
| Calculation Type | FTS |
| Calculation Method | RHF |
| Basis Set | 3-21G |
| Charge | 0 |
| Spin | Singlet |
| Total Energy (a.u.) | -231.6932240 |
| Total Energy (kcal/mol) | -145389.7241756 |
| RMS Gradient Norm | 0.00003621 |
| Imaginary Frequency | -818 cm-1 |
| Dipole Moment | 0.0003 Debye |
| Terminal bond lengths | 2.02Å |
| Point Group | C2h (after symmetrisation of the molecule) |
| Log File | File:FREEZE COORDINATE OPTIMISATION.LOG |
The differences in the thermochemistry data between the two methods was negligible. The imaginary frequency at -818 cm-1 corresponded again to the Cope Rearrangement, whereby the vibration indicated the bon formation and breakage at the terminal Carbon atoms by undergoing a six atom transition state.
QST2 Method (boat)
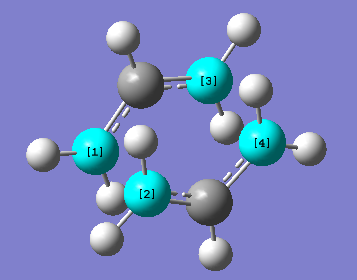
The third investigated method was the QST2 method which was applied onto the cyclohexane boat structure. The QST2 method uses the labeling system of the molecules. It has to be computed in Gaussview which molecule transforms to which (here according to the mechanism of the Cope Rearrangement). When starting off with two 1,5-hexadiene molecules, the molecules have to be set to the correct angles and conformation to ensure the formation of a boat transition state. This was done by setting the dihedral angle at the 4x central C-C bonds to 0º and the angles between the terminal C-C-C bonds to 100º, as illustrated below.
Any other set angles and can lead to the formation of other transition states, such as the chair-like transition state shown below.
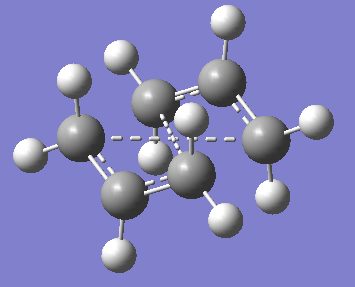
As a result, a boat transition state was obtained with a bond distance of 2.14Å between the terminal Carbon atoms (2.78Å between the two central Carbon atoms). The following two tables show all relevant data on the boat transition state including energy and thermochemistry data.
| Category | Result |
|---|---|
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RHF |
| Basis Set | 3-21G |
| Charge | 0 |
| Spin | Singlet |
| Total Energy (a.u.) | -231.60280200 |
| Total Energy (kcal/mol) | -608073.20297156 |
| RMS Gradient Norm | 0.00007080 |
| Imaginary Frequency | -839.94 cm-1 |
| Dipole Moment | 0.1579 Debye |
| Terminal bond lengths | 2.14Å |
| Point Group | C2v (after symmetrisation of the molecule) |
| Log File | File:QST2 BOAT.LOG |
QST2: Boat transition state (Cope Rearrangement - imaginary frequency)
(if the animation is not activated please click on it)
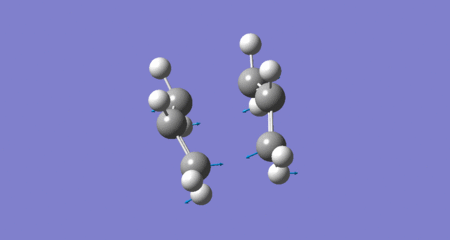
| Energy classification | Respective equation | Energy in a.u. (at 298K) | Energy in kcal/mol (298K) |
|---|---|---|---|
| Sum of electronic and zero-point energies | E = Eelec + ZPE | -231.450928 | -145237.681108 |
| Sum of electronic and thermal energies | E(298K) = E(0K) + Evib + Erot + Etrans | -231.445299 | -145234.148856 |
| Sum of electronic and thermal enthalpies | H = E(298K) RT | -231.444355 | -145233.556487 |
| Sum of electronic and thermal free energies | G = H -TS | -231.479774 | -145255.78225 |
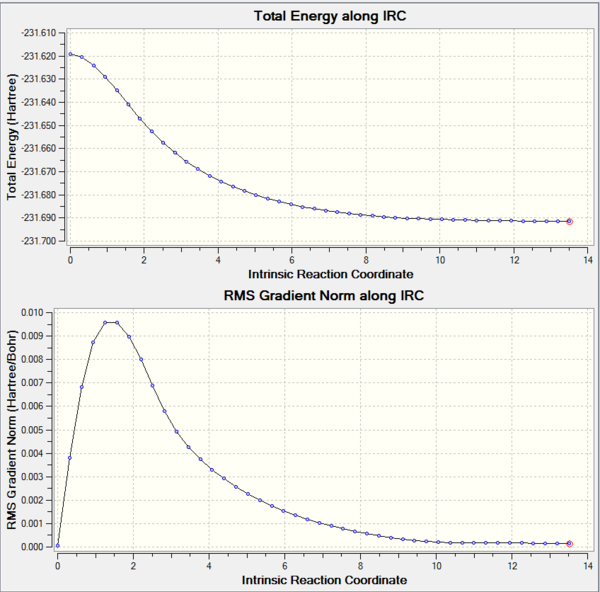
IRC of the boat transition state structure
The IRC (Intrinsic reaction coordinate) is a tool to demonstrate the reaction mechanism a molecule undergoes starting with the starting material and ending with the formation of the product via the transition state. The IRC calculations were run by submitting an IRC job type (50 steps, calculate one way, calculate force constant always) into Gaussview with the H/F3-21G method for both the output (LOG-files) of the respective conformers. This computational tool was used in the case of both the chair and boat transition states, as can be seen in the diagrams below:
Calculations regarding the Chair structure
To calculate the IRC for the chair conformer, only 44 steps of the indicated max. 50 steps were considered by the software. The corresponding minimum energy is -231.61932230 a.u. and the minimum value for the RMS gradient was 0.00004545. The given point group for the product was observed to be C2. Therefore it can be concluded with respect to the formed structure and point group that the gauche 2 conformer is eqivalent to the product.
Calculations regarding the Boat structure
The IRC calculation was carried out on the LOG file which was obtained from the previous QST2 calculation. To calculate the IRC for the boat conformer, only 45 steps of the indicated max. 50 steps were considered by the software. The corresponding minimum energy is -231.60280200 a.u. and the minimum value for the RMS gradient was 0.00007069. The given point group for the product was observed to be Cs. With regards to the given appendix in the script no structure can however be allocated with Cs symmetry and it becomes clear that Gaussview in the IRC job remodeled the structure that was submitted from the QST2 exercise, i.e. the form into which the Reactant and Product had to be modeled into to form the boat conformer instead of the chair. This could be avoided in future work, when carrying out the QST3 exercise instead or calculating the boat transition state via for example the Hessian method.
From the animations it can be clearly observed which one corresponds to the boat and which one corresponds to the chair, when looking at the final movement of the terminal Carbon atoms (in the boat structure both ends move to the same direction). The animations also show when the bond was formed i.e. locate the correct transition state. The diagrams for each conformer outline that a metastable product was formed due to the plateau region at the right end of the graph. This corresponds to a local energy minimum and the total energy of the product formed in this reaction. The RMS gradient plot shows the same trend and by approaching 0.000 asymptotically it can again be concluded that the correct product was formed. Nevertheless, there are three approaches that should be considered to absolutely confirm the formation of the final product.
- Running a further minimisation from the last step given (44 or 45) in the IRC calculation
- Increasing the number of steps for the IRC calculation when submitting into Gaussview
- Calculating the Force constant at every step
The first step was carried out and it was observed that the same minimum energy was obtained as shows below table for the chair conformer.
| Category | Result |
|---|---|
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RHF |
| Basis Set | 3-21G |
| Charge | 0 |
| Spin | Singlet |
| Total Energy (a.u.) | -231.69166702 |
| Total Energy (kcal/mol) | -145388.74715567 |
| RMS Gradient Norm | 0.00000475 |
| Dipole Moment | 0.3806 Debye |
| Log File | File:IRC CALCULATION PIC 44 OPT.LOG |
From the results above it can be seen that the reoptimisation does not make a large difference nor improvement. The second suggestion can be ignored as the maximum amount of steps was 50 and only 44 (chair), 45(boat) were needed for the IRC calculation, hence a larger amount of steps would not have made a difference. The third suggestion was not considered either, since the force constant was set to be always calculated and hence it would not have given a better result. Therefore only the first suggestion can give a better result, nevertheless no big energy difference results from it.
Activation Energies
The final exercise was about the consideration of the activation energies (=energy difference between the reactant and transition state structure) for both chair and boat conformers and a final summary of the results obtained in previous exercises. The first step was the reoptimisation of the lower level HF-3-21G) to a higher level i.e. B3LYP-6-31G(d).
Chair reoptimisation
Chair_higher level opt |
| Category | Result |
|---|---|
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d) |
| Charge | 0 |
| Spin | Singlet |
| Total Energy (a.u.) | -234.55698303 |
| Total Energy (kcal/mol) | -147186.76048199 |
| RMS Gradient Norm | 0.00001198 |
| Imaginary Frequency | -565.54 cm-1 |
| Terminal C atoms distance | 1.96755 Å |
| Dipole Moment | 0.0000 Debye |
| Energy classification | Respective equation | Energy in a.u. (at 298K) | Energy in kcal/mol (298K) |
|---|---|---|---|
| Sum of electronic and zero-point energies | E = Eelec + ZPE | -234.414929 | -147097.620213 |
| Sum of electronic and thermal energies | E(298K) = E(0K) + Evib + Erot + Etrans | -234.409009 | -147093.905356 |
| Sum of electronic and thermal enthalpies | H = E(298K) RT | -234.408065 | -147093.312987 |
| Sum of electronic and thermal free energies | G = H -TS | -234.443814 | -147115.745828 |
Boat Reoptimisation
Boat_higher level opt |
| Category | Result |
|---|---|
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d) |
| Charge | 0 |
| Spin | Singlet |
| Total Energy (a.u.) | -234.54309307 |
| Total Energy (kcal/mol) | -147178.04439864 |
| RMS Gradient Norm | 0.00000193 |
| Imaginary Frequency | -530.30 cm-1 |
| Terminal C atoms distance | 2.20679 Å |
| Dipole Moment | 0.0613 Debye |
| Energy classification | Respective equation | Energy in a.u. (at 298K) | Energy in kcal/mol (298K) |
|---|---|---|---|
| Sum of electronic and zero-point energies | E = Eelec + ZPE | -234.402343 | -147089.722377 |
| Sum of electronic and thermal energies | E(298K) = E(0K) + Evib + Erot + Etrans | -234.396008 | -147085.747104 |
| Sum of electronic and thermal enthalpies | H = E(298K) RT | -234.395064 | 147085.154735 |
| Sum of electronic and thermal free energies | G = H -TS | -234.443814 | -147115.745828 |
The above calculations show in both cases (chair and boat) that more accurate results can be obtained with the higher level optimisation method. As already mentioned it is not possible however to directly calculate the energy values that are obtained from the two methods, as Hartree-Fock and DFT are based on different assumptions. All transition state optimisations were carried out on the anti 2 conformer, hence its energy is considered as the energy of reactant for the activation energy calculations.
From the data obtained from the higher level reoptimisation the difference in energy can be calculated and teh activation energies can be worked out for both chair and boat structures. It was observed that the calculated energies differed between the lower level and higher level optimisation. The same was experienced in the case of the anti 2 conformer where different methods gave different energy values.
Summary of energy values (all units are given in a.u.)
| HF/3-21G | B3LYP/6-31G* | |||||
|---|---|---|---|---|---|---|
| Electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | Electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | |
| at 0 K | at 298.15 K | at 0 K | at 298.15 K | |||
| Chair TS | -231.61932230 | -231.466705 | -231.461338 | -234.55698303 | -234.414929 | -234.409009 |
| Boat TS | -231.602802 | -231.450928 | -231.445300 | -234.54309307 | -234.402343 | -234.396008 |
| Reactant (anti2) | -231.69253528 | -231.539539 | -231.532565 | -234.61170280 | -234.469212 | -234.461856 |
*1 hartree = 627.509 kcal/mol
Summary of the activation energies to predict transition state selectivity (in kcal/mol)
| HF/3-21G | HF/3-21G | B3LYP/6-31G* | B3LYP/6-31G* | Expt. | |
| at 0 K | at 298.15 K | at 0 K | at 298.15 K | at 0 K | |
| ΔE (Chair) | 45.89 | 44.87 | 34.20 | 37.07 | 33.5 ± 0.5 |
| ΔE (Boat) | 55.82 | 54.98 | 42.13 | 45.26 | 44.7 ± 2.0 |
Values labelled as Expt. refer to the ones given in the lab script. The results obtained are fairly within the range of where we would expect them from experiments with some deviations. This outlines once again the importance of computational chemistry and its precision that is extremely challenging to achieve in the lab. The values obtained in the calculations agree quite accurately with the ones quoted in the script. The second table highlights which transition state is preferred at respective conditions and it can be observed that the chair transition state is generally lower in energy and hence more stable. The values obtained from the higher level method ((B3LYP 6-31G(d)) method match the experimental values better than the ones obtaoned by the Hartree-Fock method. The reason is most probably because the higher level method uses less approximations, takes longer and thus provides results that are more precise.
Diels Alder pericyclic Cycloaddition
The Diels Alder reaction represents a classic type of periciclic rearrangement whereby 6π electrons are moved in a concerted fashion, forming two new Carbon-Carbon bonds and one double bond. This cycloaddition where a diene is attacked by a dienophile is triggered by heat and can form both the exo and endo product. A successful Diels Alder reaction depends on the symmetry overlap between the two molecules i.e. only if they are of the same symmetry (asymmetric + asymmetric or symmetric + symmetric) a reaction can occur. The cycloadditions considered in the following calculations are all of the 4n+2 type and hence occur via Huckel Topology in a suprafacial fashion. The following exercises consider two examples where the transition states of Diels Alder cycloaddition examples were modeled and annalysed by methods that were explored in the previous part.
Cis-Butadiene and ethene cycloaddtion: Optimisation and Transition States
Below is the reaction scheme for the investigated Diels Alder reaction of this exercise.
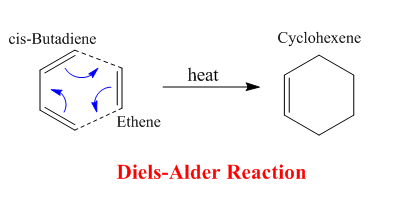
Cis-Butadiene
Cis-Butadiene and ethene were optimised and their orbitals (individual molecules and transition state) as well as their transition states including IRC analysis was calculated to understand the mechanism of the underlying reaction. Only the HOMO and LUMO molecular orbitals dictate the reactivity and hence only these orbitals were considered for the sake of this analysis.
Table 13 shows the HOMO and LUMO orbitals for cis-Butadiene (File:CIS BUTADIENE OPT+FREQ.LOG). To view the symmetry, the checkpoint file had to be opened.
| Molecular Orbital | HOMO | LUMO | |
|---|---|---|---|
| Image |  |

| |
| Energy in a.u. | -0.34382 | 0.01709 | |
| Symmetry | Asymmetric | Symmetric |
Regarding the symmetry it can be concluded that the HOMO has one node (=asymmetric) and the LUMO has two nodes (=asymmetric). Cis-Butadiene was optimised by the AM1 method and showed a C2v symmetry with an energy of 0.04879734 a.u..
Ethene
Table 14 shows the HOMO and LUMO orbitals for ethene (File:ETHENE OPT+FREQ.LOG)
| Molecular Orbital | HOMO | LUMO |
|---|---|---|
| Image |  |

|
| Energy in a.u. | -0.38777 | 0.05284 |
| Symmetry | Symmetric | Asymmetric |
Both the cis-Butadiene and ethene optimisations were run via the AM1 method which is important to be able to compare them and match the optimised structures together onto one window in Gaussview to be able to calculate a correct transition state. Ethene showed a D2h point group and an energy of 0.02619024 a.u.. Having analysed the optimisations of both reactants in terms of their orbital symmetry , it can already been predicted that the reaction can occur since the HOMO of cis-Butadiene has the same symmetry as the LUMO of ethene and vice versa.
Transition state for the cycloaddition between cis-Butadiene and ethene
| Molecular Orbital | HOMO | LUMO |
|---|---|---|
| Image | 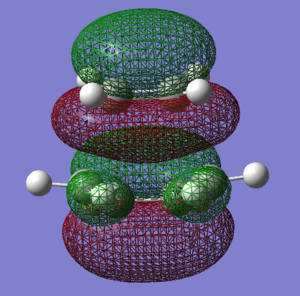 |

|
| Energy | ||
| Symmetry | Symmetric | Asymmetric |
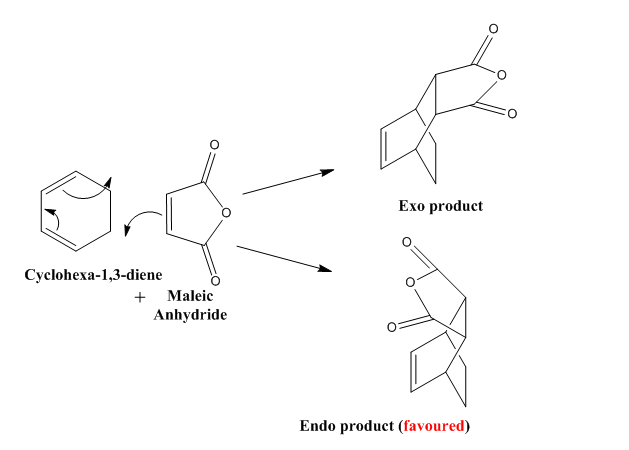
Transition State calculations for cyclohexa-1,3-diene and maleic anhydride
| Molecular Orbital | HOMO | LUMO |
|---|---|---|
| Image | 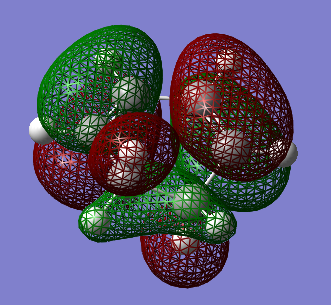 |

|
| Energy | ||
| Symmetry | Asymmetric | Symmetric |
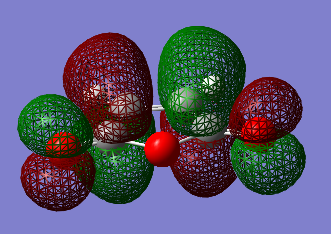
| Molecular Orbital | HOMO | LUMO |
|---|---|---|
| Image |  |
|
| Energy | ||
| Symmetry | Asymmetric | Symmetric |