Rep:Mod:Victoria3

The Cope Rearrangement

The cope rearrangemnt is a concerted process, i.e. the bonds are borken and formed in the same process, though the same cycle of electrons around the ring. The [3,3]-sigmatropic rearrangment occurs via either a 'chair' or a 'boat;' transition state. Gaussian will be used (with the B3LYP method and 6-31G* basis set) to investigate the reaction and its transition state.

Optimizing the Reactants and Products

A 1,5-hexadiene was modelled on Gaussview. This is the reactant molecule for the cope rearrangment. The diene was first drawn with an 'anti linkage' (i.e. looking along the centeral bond the substituent groups were anti periplanar (180degrees) to each other.) The structure was then 'cleaned' and optimised using the Hatree Fock method and the 3-21G basis set. When the structure had been optimised it was 'symmetrized' and the point group and energy recorded.

The same mehtod was then used on a hexadiene with a 'gauche' linkage in the centeral bond. The following structure was the result of the optimization. This shows that the Gauche confromer is more stable than the anti conformer. One reason for this is that the gauche confromer, being less 'ordered' will have a higher entropy. This greater disorder is energetically more favourable. The anti confromer is more ordered in comparison and therefore has a lower entropy and as a result is less eenrgetically favourable.

When comparing the conformers drawn and optimised to the table given in Appendix 1(http://www.ch.ic.ac.uk/wiki/index.php/Mod:phys3#Appendix_1) I found that the confemres I have drawn are 'anti2' and 'gauche3'. The energies of my optimized structures compare very well with the energies given in appendix 1. The energies fo my optimized structures, given to 5 decimal places matches the energies given in the table exactly.

**1,5-Hexadiene Conformers**
Conformer	Energy	Point Group	Conformer in appendix 1
Anti	-231.69253527	Ci	Anti 2 (-231.69254)
Gauche	-231.69266120	C1	Gauche 3 (-231.69266)

. I found that the conformers I drew were the lowest energy Anti and Gauche conformers so modelling further structures and optimising them was not necarssary.

The 'anti 2' confomrer was then used for further modelling and investigation. The first task was to further optimise the structure to a more accurate degree, using the more complex basis set 6-31G* and the B3LYP method. This reoptimised structure had an energy of -234.559670 Hatrees. This structure is therefore 7527.73KJ/mol more stable than the same structure optimized using the 3-21G basis set. The geometry does not change when the structure is reoptimized to a higher level.

In order to be able to compare the results given computationally to energies recorded experiminetally it is necarssary to compute some additional thermochemistry values. These will be calculated by carrying out a frequency calculation on the re-optimised 'anti 2' conformer. BY carrying out this frequency calculation we can also verify that the optimization has found a minimum rtaher than a maximum. This can be verified by ensuring there are no imaginary frequencies (i.e. neagtive frequencies).

The results of the calcualtion showed that the optimization had reached a minimum as there were no negative frequencies.

Viewing the output file the following data was collected:

**Anti2 Thermochemistry**
Energy Term	Energy
Sum of electronic and zero point energy	-234.416244
Sum of electronic and thermal energies	-234.408954
Sum of electronic and thermal free energies	-234.447850
Sum of electronic energies and thermal enthalpies	-234.408010

Optimizing the Chair and Boat Transistion Structures

IN this section we will use three different methods to optimise the transition states of the Cope Rearrangement. For the first transition state of the cope rearrangement, the 'chair' we will use two different methods to carry out the optimization: firstly by computing the force constants at the beginning of the calcualtion and secondly by using the redundant coordinate editor. For the second transition state , the 'boat' the QST2 method will be used.

The activation energies for the rearrangment via the chair transition state and the boat transisition state will be calcualated also to compute which transition state corresponds to the kinetic reaction and which the thermo dynamic one.

Chair Transisiton State Optimizations

In order to begin the investigation the substituenets of the transistion states must be modelled. The chair transition states involve the following fragment (essentially half the rign structure round which the electrons cycle) which was modelled on Gaussview and trhen optimized using the Hatree-Fock/ 3-21G method.

To produce the chair transiton state 2 of the optimised allyl fragements were copied and pasted into a new molecule group and manipulated to look like the transition state of the cope rearrangement. The fragments were positioned about 2.2A apart.

This structure was then optimised in two different ways to the chair transition state. An explaination of each of the two methods and their results follows.

Using the Hessian Matrix and Berny Algorithim

The first method used to optimise the transition state was by computing the force constants at the beginning. Since we have a good idea of what the transition state looks like (see above picture) this is a good method to use. The calcualations will compute the 'force constant matrix' aka 'the hessian'and optimises to a Transition State using the Berny method . This is an algorithim developed by Bernhard Schlegel. It uses the forces acting on the molecule and the force constant matrix (which is computed at the beginning of the calculation, 'once') to predict 'energetically more favourable structures and this optimises the molecular structure towards the next local minimum on the potential energy surface'. http://www.cup.uni-muenchen.de/oc/zipse/lv18099/basic.html. Hence why this method only works well when there is already a good idea of what the transisiton state looks like. This method will only find the next minimum along on the reaction coordinate so if the input structure is a long way from the transistion structure the method may not find the transition state minimum, but a local minimum closer in energy to the input structure.

The calcualtion carried out was the'Opt+Freq' calculation and the words 'Opt=NoEigen' were added to the 'addiditonal keywords' box. The reason for this is to prevent the calculation from crashing if it finds more than one imaginary frequency .An imaginary frequency is a vibration with a nagative(or very small) frequency. It is 'imaginary' because it is associated with the bonds that are being made and the bonds being broken in the rerarrangment. The bonds arent fully made or broken in the transition state but partially exist so have some vibration associated with them.

A simple explaination as to why the 'vibration' is imaginary is because it onyl related to a one way movement of the bond in question. The imaginary frequency relates to the new bond being formed, at the transtion state this bodn is only partially formed. Negative frequency relates to the movement tofomr the bond. there is no 'opposite' force, one that causes the bond to spring back lengthening again, there is only a movement of the bond shortening (i.e. fully forming) as the trnanstion state moves towards the product. The one way vibration is negative because it relates to the second derivate of the reaction coordinate function. the transtion state is at a maxima at the top of the curve of the reaction cooridnate. The second derivate is neagtive because this ia a maxima. the vibrational frequency is then related to the square root of this nagative derivative, which is obvoously an imaginary number.

The calculation only found one imaginary frequency, -817.92cm-1 with an intensity of 5.8572, which corresponds well to the -818.00cm-1 frequency expected for the Cope Rearrangement. This shows that the 'Approximate Transiiton State' above was a good approximation of what the chair transiton state looks like. Only one imaginary frequency was found and animation of this frequency clearly shows the forming/breaking bonds.

**Chair Transition State**
	Energy (Hatrees)
Electronic Energy (HF/3-21G)	-231.61932247
Electonic and Zero Point Energy (HF/3-21G)	-231.466700
Electronic and Thermal Energies (HF/3-21G)	-231.461340
Electronic and Thermal Enthalpies (HF/3-21G)	-231.460396
Electronic and Free Energies (HF/3-21G)	-231.495206

The geometry of the Chair Transition State Showed that the forming/breaking bond distances in this structure were 2.0205A.

Using the Frozen Coordinate Method

The second method used to optimise the transition state is using the redundant coordinate editor. Using this method, in the first step we freeze the bonds that are being made or broken in the transition state. These bonds are set to 2.2A, we know they are forming C-C bonds so this a reasonable length to set the bonds to. The rest of the structure is then optimised to a minimum (HF/3-21G).

In the optimised strucvture the forming/breaking C-C bonds are then unfrozen and are set to 'derivative'. The structure is then reoptimised (opt+freq, HF/3-21G) to a Transition State (Berny) using the berny algorithim and the hessian matrix (calcualted by the 'derivative' function on the forming/breaking bonds).

The result using the frozen coordinate method is that int he frist step the whole structure (with the exception of the froming/breaking bonds) is optimized to a minimum and then in the second optimisation the areas directly related to the transiton (the forming and breaking bonds) are optimized to a transiton state.

The optimised transtion state had an imaginar vibrational frequency of -817.92cm-1 with an intensity of 5.8551.

**Chair Transition State Frozen Coordinate Method**
	Energy (Hatrees)
Electronic Energy (HF/3-21G)	-231.61932247
Electonic and Zero Point Energy (HF/3-21G)	-231.466700
Electronic and Thermal Energies (HF/3-21G)	-231.461340
Electronic and Thermal Enthalpies (HF/3-21G)	-231.460396
Electronic and Free Energies (HF/3-21G)	-231.495206

The geometry fo this transiton state showed that the bond lengths of the forming/breaking bonds in this strucutre were 2.0205A. The data collected, both the energies and the geometries, by each method for the Chair Transition States matches exactly. This shows that both methods have reached the transition state.

Boat Transition State Optimisation

This optimisation will be carried out using the QST2 method. In this method we can specify the reactants and products of a reaction, labelling the atoms in each molecule the same. The QST2 calculation will then find the transition state which lies bewteen them.

For this mehtod we will use the 'anti2' molecule from one of the previous sections. For the first part of the task the anti2 isomer is copied twice, one moelcule is the reactant and one the product of the cope rearrangement and the molecules are labelled as follows:

The QST2 calculation was run (opt+freq,minimuised to a TS(QST2) 3-21G/HF). The output of this calculation is clearly not a viable structure for the boat transition state. The calcualtion does not consder the rotation around the centeral bond possible to make the product.

The solution to this problem is to begin with the rotated product and reactant. As follows:

The return of this calcualtion (again opt+freq,minimuised to a TS(QST2) 3-21G/HF) is the following Boat Transiton state for the cope Rearrangment.

**Boat Transition State**
	Energy (Hatrees)
Electronic Energy (HF/3-21G)	-231.60280208
Electonic and Zero Point Energy (HF/3-21G)	-231.450928
Electronic and Thermal Energies (HF/3-21G)	-231.445300
Electronic and Thermal Enthalpies (HF/3-21G)	-231.444355
Electronic and Free Energies (HF/3-21G)	-231.479118

The bond lengths of the fomring/breaking bonds in this transition state were measured as 2.1403A.

Intrinsic Reaction Coordinates

Although looking at transition states is very useful the transisiton states alone cannot give a good idea of what the product (or reactant) looks like. The IRC, or Intrinsic Reaction Coordinate, involves calculations which allow the strucure to move further towards the product. The IRC computes the hessian along the reaction path way and takes samll steps in terms of the geometry of the molecule following the steepest gradient of the reaction path in order to move towards the products (or reactants) of the reaction. It can therefore give a good understanding of what the product (or reactant) of the reaction will look like.

The first IRC i ran on the reaction was on the chair transition state to give an idea of what the product of the reaction would look like (that is, I ran the IRC for the forwards reaction rather than the reverse).This first calcualton was run looking at 50 points along the IRC.

As can be seen from the graph of the Reaction Gradient the IRC does not reach a plateau and therfore does not reach the lowest energy product molecule. That is, although the products will look somewhat like the last step of this IRC, since the gradient is not at a plateau the products are not at their minimum energy and therfore may look slightly different to this result.

Since this first IRC has not reached a minimum further optimisations must be carried out. There are three options for calculations to carry out in order to reach a real minimum for the products. Firstly the last point on the IRC can be used as an input and a normal optimization be run on it (Opt to a minimum , HF/3-21G or similar). Secondly the IRC can be run computing a larger number of steps in order to allow the IRC to continue to the global minimum. Finally the IRC can be rerun but computing force constants at every point (rather than just once at the begining, as in the last calculation). Computing the force constants at every step means that if the IRC has reached a local minima the calculation will not get stuck and will be able to continue to find the global nminima.

Minimising the Final Step on the IRC

By optimising the last step of the original IRC a lower energy structure is reached which is 7.76KJ/mol more energetically more favourbale than the last step of the original IRC. However, although a lower energy structure is reached this is not necarssarily a reliable representation of the product of the reaction. If the final step of the IRC was not very close in energy to the products and there was a local minima closer the optimisation may have optimised to this structure.

Adding more steps to the IRC

I reran the IRC but foudn that although it with 100 steps the calcualtion stopped after 25 steps. This is due to the IRC reaching a local minimum. This is cooroborated by the energy recorded for the structure at the last step. The energy was given as the smae as for the original IRC, -231.68871205 hatrees.

The graph shows a minimum hasn;t been reached so more steps on the IRC are necarssary.

In order to solve this problem the IRC was run calcualting the force constants at every step with 300 steps. Obviously this calcualtion would take sometime as as well as adding more steps to the calculation, to avoid falling into a local minima the frorce constants must be calculated often. This makes the process expensive and time consuming. The result was good though the structure fo the product was given as 7.74KJ/mol more stable than the last point on the original IRC.

Recalculating the Force Constants

This calculation was similar meant the force constants were calculated at every step in order to avoid falling into a local minima. The result was that the structure found was 7.73KJ/mol more stable than the structure found for the original IRC. This should also give a more realistic representation fo the products that simply reoptimizing the last step on the IRC plot would as this method is still following the reaction coordinate.

Results of IRCs

**Intrinsic Reaction Coordinate**
Method	Energy (Hatrees)	Forming Bond Length A	Breaking Bond Length A
Oringal IRC	-231.68871205	3.34	1.56
Optimization of last point on IRC	-231.69166702	4.39	1.55
Adding more point (fallen into local minimum)	-231.68871205	3.34	1.56
Adding more point(300 points	-231.6916618	4.39	1.55
Calculating force constants at every point	-231.69165717	4.35	1.55

Activation Energies

In order to find the activation energies for the reaction moving to each of the boat and the chair transisition state I considered how the reaction would progress. I used the lowest energy confromer of the 1,5-hexadiene as the starting point. The thermo chemistry fo this confromer was then calculated using an opt+freq calculation 3-21G/HF. These values (of the reactant) could then be compared to the same values at the transition state. the difference would give the activation energies.

The electronic and zero point energies of the 'gauche 3' confomer: -231.539486 hatrees. This will be used to find the activation energy at 0K. The electronic and Thermal energies of the 'Gauch 3' conformer: -231.532646 hatrees. This will be used to find the activation energy at 298K.

**Activation Energies**
	Chair at 0K	Chair at 298K	Boat at 0K	Boat at 298K
activation energy (hatrees)	0.072786	0.071306	0.081718	0.087346
activation energy (Kcal/mol)	45.6739143	44.7452001	51.2788301	54.8104542
activation energy (ref)(Kcal/mol)	45.70	44.69	55.60	54.76
activation energy experimental (Kcal/mol)	33.5+-0.5		44.7+-2.0

There is good agreement between the values I have computed and the values in the referance:https://www.ch.imperial.ac.uk/wiki/index.php/Mod:phys3. That the Gauche 3 optimised structure and the optimised chair and boat transition states were the lowest energy forms. the agreement with the experimental values is quite good, though it shows that the cpmputed values are often a little higher than the real values.

Diels Alder Investigations

The Deils Alder Reaction is a pericyclic reaction. electrons fomr conjugated pi systems cyle round a ring like transition state using pi bonds to form new sigma bonds. The following investgation is into this reacton.

The first task was to model this reaction:

The first objective was to model cis butadiene on Gaussview and clean and optimise the structure. This structure had to be cleaned because i found that without cleaning the optimisation produced a cis butadiene which was non-planar, however all 4 carbon atoms in the moelcule are sp2 hybridised and therfore have trignoal planar sp2 orbitals for interaction, the results butadiene moelcule should therefore be planar. The structure was optimised using a semi empircal method, AM1. the enry for the cis butadieen was 0.04879719 hatress.. (the value when it was optimised with the HF/3-21G method was -154.05394316 hatrees). The structure had a point group of C2v.

The HOMO and LUMO Molecular Orbitals were then computed.

The LUMO MO was found to be symmetric as a plane of symmetry exists (the xz plane). The HOMO is not symmetric, its anti symertic becasue although the shapes of the orbital are symetric in the xz plane the phase of the orbitals is not symmetric.The energy of the HOMO was -3.4381 Hatrees and the LUMO 0.01707 Hatrees (when calculated by the HF/3-21G method the HOMO had an energy of -0.32599 and the LUMO 0.12366 Hatrees). The MOs show the pi sysmtes in both the ethene and the cis butadiene. It6 is the voerlap and interaction of these pi orbitals that will create the sigma bonds in the reaction.

The next task was to compute the transition state for this reaction. The areas of bond forming and at the ends of the pi conjugated system of the butadiene and each carbon fo the ethene and also the single bond between the two pi bonds of the cis butadiene which will become a pi bond. The areas of bond breaking are each pi bond of the cis butadien which willl both become sigma bonds in the product and the pi bond of the ethene structure which will become a sigma bond. In order to compute the transition state accurately it is important to have a good idea of how the transisiton state will look. In the first calcualtions I carried out to find the transition state (using the TS(berny) algorithim) the sigma bond forming areas were modelled to be 2.0A apart. The calculation failed. This is due to the fact that bonds in Gaussian are based on a pre-determined length between atoms. the molecules for my reaction were too close together which means that gaussian treated them as if they were already bonded and therefore no transistion state was found.

The calculation was rerun with longer bond lengths (2.2A). This calcualtion did find a transiton state with an imaginary frequency which shows the bonds forming. This is proof that the optimization foud a transition state as the single imaginary frequnecy represents symmetric bonds being formed. The energy of this transtion state was 0.20534216 hatrees. The imagiary frequency was found at -319.98cm-1 with an intensity of 0.3131.

The bond lengths for the fomring sigma bonds were 2.14354A. The length between the two Sp2 carbons (pi bond) was 1.33781A and the Sp3-Sp3 bond length for a sigma C-C bond was 1.56954. This shows us that in the transition state the bonds are not fully fomred. Neverthe;ess, the bond is a shorter distance than the sum of two Carbon Van Der Waals radii (1.7A) so clearly the interactiion here involved the overlap of the 'effective radii' of the carbon atoms involved. Also, they have a very long bond length compared to the bond length of the other carbon carbon bonds in the molecule. The bond length of a C-C sigma bond (sp3 bond)is 1.54A and the bond length of a C=C double bond (sp2 bond) is 1.34A. In the transition state the sp2sp2 bond and the sp3sp3 bond are far closer to their literature values than the sp3-sp3 sigma bonds that are forming. This suggests that the reaction proceeds by lengthening the ethene bond to be closer to the length of a sigma bond and shortening the simga bond in the cis butadiene before fomring the new sigma bonds and breaking the pi bonds in the diene (which in the transisition state are 1.48325A).

The Transition states imaginary frequency shows that the formation of the sigma bonds is synchronous, they occur at the smae time, the molecule vibrateds in a symmetric fashion. teh smallest positive frequency is at 141.04cm-1 (with a small intensity of 0.4198). This frequency shows the sigma bonds forming in a non synchronous fashion.

The computed MOs for the Diels Alder reaction of cis-butadiene and ethene show the HOMO as anti-symmetric (a) and the LUMO as symmetric (s). The HOMO lcearly shows the bonding interaction betweeen the two molecules. It is within this 'bonding' region that we see the new sigma bonds being formed. When a reaction occurs the MOs which are 'mixing' must have a similar symmerty, ie, they must both be symmetric or both be anti symmetric. The LUMO of the cis butadiene and the HOMO of the ethene are therefore 'allowed' to mix as they both have symmetric symmetry, and the HOMO of butadiene and the LUMO of ethene are allowed to mix because they are both anti-symmetric. the matching symmetries of the HOMO-LUMO means the reaction is 'allowed' to proceed where these orbitals are mixing.

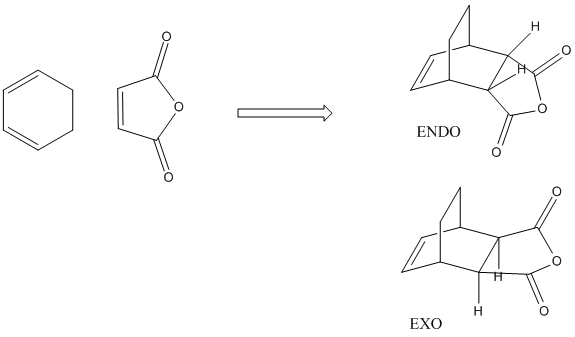
The Diels Alder reaction of cyclohexa-1,3-diene reaction with maleic anhydride

This reaction is another Diels alder reaction. The task in this section is to examine the two routes by which the reaction could proceed, i.e. via the EXO or ENDO reaction.

An approximate guess at the transition state for each conformer was modelled on Gaussview. I order to optimise the approximate transisito states I chose to use the forzen coordinate method. The conformers were modelled with the two molecules around 2.2A aprat and this is the length at which the bodns were set.

**ENDO and EXO Transisiton States**
	ENDO	EXO
Transition state	EXO transition state	ENDO transisiton state
Imaginary frequnecy of transntion state	-647.86cm-1 (intensity 67.48)	-644.40cm-1 (intensity 36.43)
Energy of transition state (hatrees)	-605.60359125	-605.61036828
Highest Occupied Molecular Orbtials	EXO HOMO	ENDO HOMO
	EXO HOMO	ENDO HOMO
Geometry	Distance between the C=OOC=O fragment and the 'oposite'-CH2-CH2- fragment: 2.92A	Distance between the C=OOC=O fragment and the 'oposite'-CH-CH- fragment: 2.85A
	Distance of new sigma forming bonds	Distance of new sigma forming bonds: 2.23A
	Distance between -CH=CH- in anhydride and -CH=CH- in diene: 2.72A	Distance between -CH=CH- in anhydride and -CH2-CH2- in diene: 2.78A

The endo transition state is more stable than the exo transition state by 17.79KJ/mol. The lower energy transition state means taht in this kinetically controlled reaction the endo from is favourable as a product.

The result of this reaction is that primarily the endo product is formed, despite the product being less stable than the exo product. In the exo product we can see that there is less steric strain between the Hydrogen group on the sp3 carbon on diene and the H on the maleic anhydride. In the exo form the gap between these two groups is much larger than in the endo form in which the hydrogen atoms are pointing towards each other, inducing steric strain. The more important origin of steric strina is the strain between, in the endo, the C=OOC=C and -CH-CH- group on the diene and in the exo, the C=OOC=C and the -CH2-CH2- gourp on the diene. as we can see form the MO diagrams in the exo form the larger CH2-CH2 gourp has tetrahederal carbon centres whose H atoms point directly towards the large electron dense Oxygen atoms on the anhydride. This cuases unfavourbale steric interactions. In the endo form however the Oxygen rich fragemtn is onyl interacting with -CH-CH- so there is far less steric interaction. This means the EXO form is more sterically strained.

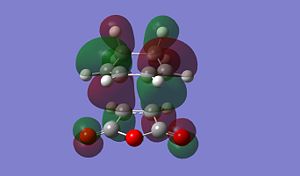
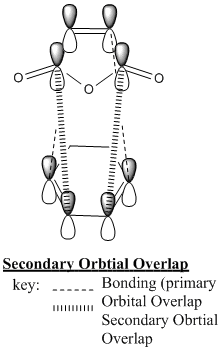
From the MO diagrmas we can see that there are two 'planes' of MOs in the molecule. In both confromers we can see that there is overlap betwen the -HC=CH- fragemnt of the diene moelcule (this is the pi bond which is being formed in the reaction) and the C(=O)OC(=O) fragment of the maleic anhydride. this is 'Secondary Orbital Overlap' that stabilises the endo transition state and causes it to be the predominant product. In the endo from we can see that the two 'planes' of orbtials are more 'lined up' where as in the exo from these orbitals are more staggered. The lining up of the orbitals int he endo form causes an interaction which is favourable and stabilises the transition state. the lack of this orbital overlap in the exo form menas it is not stabilised in this way. The secondary orbital overlap stabilisation has a greater effect than the steric destabilisation so the endo form has a more stable transisiton state.

DOIs

http://dx.doi.org/10042/to-2897 ENDO transtition state http://dx.doi.org/10042/to-2898 EXO transition state