Rep:Mod:Victoria2
Investigation of the BH3 Molecule
[[1]] This is the BH3 Opt. [[2]] This is the BH3 Freq [[3]] This is the BH3 POP
The first task was to model BH3 on Gaussview. The geometry was optimized and the structure examined. The MOs of the molecule were also examined and the vibrations of the bonds computed.
Modelling BH3 on Gaussview ONce the simple task of drawing the BH3 molecule was comolete the structure could be optimised. The optimization finds the 'best' (most stable, lowest energy) postition for the atoms in the molecule. Gaussian was used to run these calculations solving the Schrondinger Equation, making certain approximiations as outlined by the method 'B3LYP'. The basis set Gaussian was instructed to use was '3-21G'; this basis set is relativley simple, whilst it means the calculations can be carried out very quickley (the optimization took only a few seconds) it means the results are often not highly accurate.

I found that when the structure was returned after the optimisation the bonds were missing from the structure. Whilst thsi seems alarming it is to be expected. Gaussian works on the basis that bonds are given certain limits which are 'pre-defined'. Bonds that exceed this limit are not drawn as bonds in the structure Gaussian produces. This however does not mean that the bodns don't exist in the structure. Bondsa are area of electron denisty and whilst the program does not draw the line that usually represents a bond it does recognise the area of electron density that exists between the two bonded atoms.
The optimised structure was returned and the following data recorded:
| B-H Bond Length | H-B-H Bond Angle | Energy | Point Group |
|---|---|---|---|
| 1.19 | 120.00 | -26.46 | D3h |
The MO's of the BH3 Molecule
The MO's of the BH3 molecule were also examined. The calculations carried out by Gaussian using the basis set
The following MOs were computed by the gaussian calculations:
 |
 |
 |
 |
 |
 |
 |
 |
The MO diagram was drawn on chemdraw and the LCAO representations can be found in the diagram following:
aftre examining the MO diagram and the ccaluclated orbitals I found there was very good agreement between them. The orbitals computed by gaussian have a lot of resemblence to the LCAO MOs. The first orbital computed by gaussian does not appear on the MO diagram as it is not a valance orbital. This orbital is the 1s2 orbital of the Boron atom. It is very deep in energy compared to the other Molecular Orbitals (-6.81 au) and therefore is not seen on the MO diagram. The next orbital, MO2, calculated by gaussian looks alot like the all bonding 1a1' orbital (energy -0.48 au). MO3 and MO4 look like the bonding degenrate 1e' orbitals (-0.33 au). MO5 is the p orbital which is non bonding in the MO diagram (-0.08 au). MO6 is the antibonding) (note the positive energy) 3a1' orbital (0.04 au). The final orbitals MO7 and MO8 are the anti bonding 2e' orbtials (0.11 au). As can be seen these results fit very well with the MO diagram. The lumo orbitals are perhaps not as similar to the computational results but overall the agreement is good. The reason for this may be because the lumos are less well defined as they have no electron density and the calcualtions therefore don't work as well. SO whilst the compuational analysis of the MO's is useful thwe accuracy of the LUMOs calulated is not as good as for the occupied orbitals.
The Vibrational Analysis of BH3
| Frequency | Vibration | Intensity | Point Group |
|---|---|---|---|
| 1144.15 |  |
92.9 | |
| 1203.64 |  |
12.3 | |
| 1203.64 |  |
12.3 | |
| 2598.42 |  |
0.0 | |
| 2737.44 |  |
103.7 | |
| 2737.44 |  |
103.7 |
Investigation of the BCl3 Molecule
[[4]] This is the BCl3 Opt [[5]] This is the BCl3 freq
The BCl3 molcule was investigated in much the same way. The structure was drawn and the geomtery optimised. Gaussian was then used to run FREQ calcualtions which are used to compute the vibrations of the molecule. Both the optimization and the frequency calcualtions were run using the LANL2MB basis set/pseudo potential and the RB3LYP method. The same basis set and method had to be used to optimise the geometry and to calculate the frequencies of the molecules vibrations as otherwise the results would not be comparable. That is, the results form the optimization were used as the input for the frequency calucaltion and had the basis sets and methods not been the same the frequency calucaltiosn would not have been able to use and build on the optimisation results.
Using this method and basis set the optimization calculation took 7.0 seconds and the frequency analysis took 11.0 seconds.
The frequency analysis was run in order to ensure that the geometry optimisation that was run found as minima rather than another point where the gradient of the energy surface was zero(i.e. a maxima). By analysing the frequecies we can prove that the optimization found a minima as the frequencies of the vibrations will be positive. The frequencys of the vibrations are a second differentiation of the energy surface. The second differentiation of a function can be used to determine if the point is a maxima is a minima or a maxima. If the frequecies are positive an energy minima has been found (if negative frequecies are found the eneryg is at a maxima).
| B-Cl Bond Length | Lit. Value | Cl-B-Cl Bond Angle | Lit. Value | Dipole Moment | Lit. Value | Energy | Point Group |
|---|---|---|---|---|---|---|---|
| 187 pm | 175pm | 120 | 120 | 0.00 | 0.00 | -69.44 Hatrees | D3h |
As can be seen from the table the agreement between the literatrue values and the calculated values is good. The calucalted bond length is slighty longer than in the real structure.
The bond angle is as expected, 120 in the trigonal planar structure. This is the expected angle as the molecule is symtrical. The symmtry gaussian uses is D3h, this is the symmetry of the real molecule as it has a C3 rotational axis, 3 C2 roational axis and a sigma h plane of symmtry.
The Vibrational Analysis of BCl3
The vibrational analysis of the BCl3 molecule was carried out and it was found that there were 6 vibrations for this molecule. The following table describes the vibration and their intensity.
| Frequency | Vibration | Intensity |
|---|---|---|
| 214.13 |  |
3.9341 |
| 214.13 |  |
3.9343 |
| 376.94 |  |
43.7751 |
| 417.38 |  |
0.0000 |
| 939.47 |  |
258.6856 |
| 939.47 |  |
258.6884 |
Investigating the Cis and Trans Isomers of a Transition Metal Complex
http://dx.doi.org/10042/to-2831 http://dx.doi.org/10042/to-2833
http://dx.doi.org/10042/to-2835
http://dx.doi.org/10042/to-2834
This task involved the investigation of the cis and trans isomers of a Molybdenum complex, Mo(CO)4(PCl3)2. A similar Molydenum complex, (Mo(CO)4(PPh3)2, was produced and investigated by IR in second year synthesis lab. IN this experiment it was found that the IR spectrum is very closely related to the symmetry of the complex. The trans isomer, which has greater symmetry, had only 1 band of vibration for the CO ligands, the cis isomer however, which has less symmetry, showed 3 vibrational bands. In this task the two Mo(CO)4(PCl3)2 complexes will be modelled on Gaussview, optimised (loosely first) by Gaussain and then be analysed vibrationally by a Gaussian calculated. The aim is to investgiate if the computation produces the same results found experimentally.



Methodology
In this task, unlike in the first tasks, a 'pseudo potential' must be used. The transisiton metal complex has many electrons and in order to simplify the calcualtions a pseudo potential is used. The pseudo potential asigns a function to a set of electrons (18e-) instead of giving each electron its own function. This will allow the calculations to run quicker. In the initial optimization the 'LanL2MB' pseudo potiential was used, the equivalent to a 3-21G basis set and in the 2nd optimization adn frequency analysis 'LAL2DZ' was used which is the equivalent to 6-21G. or this task aslonit was found that the structure calculated form the optimisation didn't have some bonds drawn in. This is not because the regions fo electron density (i.e. bonds) do not exist in these areas. It is becasue the bonds exceed Gaussians pre-determined lengths for these bonds.
Energies of the Trans and Cis Isomers of Mo(CO)4(PCl)3
The energies of the isomers follows:
| Isomer | Energy (hatrees) |
|---|---|
| Cis | -623.577 |
| Trans | -623.576 |
The Trans isomer had a slightly lower energy and wa therefore slightly more stable. This is due to the larger PCl3 gorups being further away form each other and therefore avoiding the steric interactions which the PCl3 groups in the cis isomer experience, increasing the enrgy and destabilising the cis isomer.
The difference in energy between the structures however is very small, 2.73KJ/mol.
There was also, unsurpisingly, found to be a difference in the dipoles of each of the isomers. The Trans isomer had a dipole of 0.31D where as the Cis isomer had a dipole of 1.31D. The cis isomer had a larger dipole becasue the PCl3 groups, which have very electronegative chlorine atoms on them, were both on the same side fo the molecule. The trans had a smaller dipole becasue the PCl3 gorups, at 180degrees to each other somewhat cancelled out the dipole each created.
The geometry of the Trans structure was found to match up well with literature values for a similar molecule. The agreement is good. The reason 2 values are given for the Mo-C length and the C-Mo-C angle is probably die to the slight effect the oreination of the phosphorous gourp has. In 3 groups can not be in exactly the same position in relation to all the CO groups, which means there will be a slight disagreement in the values for each gorup depending on theri relation to the PX3 gourps X substituents.
| Bond length(A) or Angle(degrees) | Computed Value | Literature Value[1] |
|---|---|---|
| Mo-P | 2.44 | 2.50 |
| Mo-C | 2.06, 2.06 | 2.01, 2.06 |
| C-O | 1.17 | 1.16 |
| P-Mo-P | 177.39, 182.613 (av.180.00) | 180.00 |
| P-Mo-C | 90.68, 89.33 | 92.0, 87.2 |
| C-Mo-C | 90.50 | 92.1 |
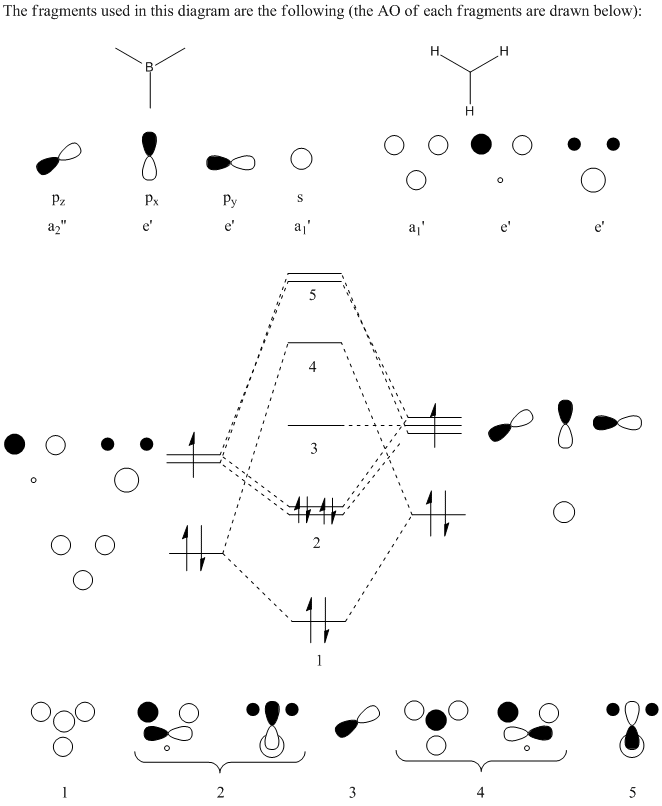
The Infra Red analysis of the Cis and Trans Isomers of the Molybdenum Complexes
The frequency analysis of the two molecules revealed that the Cis isomer showed 3 vibratational bands for the C-O strecthes and the Trans isomer showed 1.
| Complex | IR CO stretches (cm-1) | Intensity | Literature Value Stretch (cm-1) |
|---|---|---|---|
| Cis | 1945.28 | 762.67 | 1860.00 |
| 1948.66 | 1498.56 | 1889.65 | |
| 1958.34 | 633.06 | 2012.75 | |
| Trans | 1950.42 | 1475.38 | 1948.26 |
| 1951.05 | 1466.79 | ||
| 1977.33 | 0.65 |
NB: Literature data is taken from the Year 2 experiment, synthesis lab, 5S.

As can be seen from the table there were actually 3 trans C-O strecthes recorded. However looking at the intesnity, one strecth has such a low intensity it is negligable and can be ignored. For the other 2 strecthes we find that the virbtation frequency is very similar. These can therefore be grouped together and assumed to be one stetch due to their similarity.
FOr the trans Isomer the data fits well with the literature value. The Cis data does not fit as well. This may be due to impurities in the product from the experiment. There is good agreement however that for the cis isomer there are 3 bands of strecthing and for the trans there is one.
The reason there are 3 vibrational stercthes for the cis and only one for the trans is due to the symmetry of the trans molecule. In the Trans isomer all the CO groups are in the same environment with the same relationto the PCl3 gourps. On the other hand in the cis isomer the CO groups are not all in the same environment in realation to the PCl3 group. It is the effect fo this lack of symmetry that results in more CO streches being recorded.
Mini Project: An Investigation into the Schlenk Equillibrium
http://dx.doi.org/10042/to-2838 Molecule 1 opt
http://dx.doi.org/10042/to-2839 Molecule 2 opt
http://dx.doi.org/10042/to-2841 Molecule 3 opt
http://dx.doi.org/10042/to-2842 Molecule 4 opt
http://dx.doi.org/10042/to-2843 Molecule 2 freq
The mini project I chose to investigate was the Schlenk Equillibrium. When the grignard rewagent is in solution the Schlenk Equillibrium shows that not all the conformers of the dimerized grignard reagents are the same. The proportions of each isomer is dependant (amongst other factors) upon the electroonic nature of the 'R' group and the halide group and the type of solvent. I have chosen to study the schlenk equillibrium for my mini project as there are many interesting questions posed by it. Some of which i will attempt to adress in my project.
Methodology The method used for this project does not differ enormously from the method used for the transition metal isomerism task above. Once an isomer has been modelled in gaussview it will be submitted to the super computer for a 'loose' optimization. This will be calculated using the 'LanL2MB' pseudo potential which is equivalent to the '3-21g' basis set. It is important to note that for all the calculations carried out by gaussian for this project that a pseudo potential be used. This will speed up the calculations for the larger atoms on in the molecule. The halide atoms have many electrons and each electron has its own potential. By usign the pseudo potential gaussian can assign one fuction of potential to each group of electrons, thereby reducing the complexity of the caluclations.
After the LanL2B loose optimization the output of this will be adjusted slightly and submitted for a complete optimisation with a more complex basis set. This optimisation will be carried out with the LAL2DZ pseudo , which is the equivalnet to the '6-31G' basis set, which is more accurate than the '3-21G'. This will give more accurate results for the optimisation.
How are dative bonds represented?
In the grignard dimer the halide bridge is respresented as one bond with a sharing of electrons between the Mg atom and the halide and one dative covlavent bond where the halide donates 2 electrons in a bond to the Mg atom. The first queston I wish to inveistgate for my mini project is how this sharing fo electrons is represented by the MO's computed by Gaussian. Each halide atom must overall share 3 electrons in order to complete the octet for each fo the 2 Mg atoms. The question that will be answered in this section is ; how is this bridging by the halides represented computationally.
The MOs were computed through gaussain and there was found to be 96 occupied Molecular Orbitals. Looking at the orbital pictures we can see that the expected datvie covlanet bond does not appear. In order to understand the MO's that were computed we must first understand the electronic configurations of the atoms involved.
The electronic configuration fo Mg is [1s22s23p63s2] we are interested in the valence electrons, so an atom of magnesium has 2 3s electrons in its valence shell. The tetrahedral magnesium forms a 2e/2c (2electron/2centre) bond each with the O of the THF and the C of the methyl organic ligand. This bonding allows Mg to have a valence shell which has acess to 4 electons. In order to fullfill the Octet rule and have increased stability the Mg must have 4 more electrons in its valence shell. Mg can be in a 1+ oxidation state, giving it another electron in order to make a 2c/2e bond to the Br halide. It now has 6 electrons. The final 2 electrons are a donation from the Br which has 3 lone pairs of electrons (configuration:[Ar]4s23d104p5, with a valnece shell with 7e). From this theory we might therefore expect the computation to show the Br with 2 p orbitals occupied, a bonding orbital to Mg and another orbital which represents a dative covalent pair from a p orbtial.
The followign diagrms show the MOs related to the dative covalent bond area
 |
 |
 |
 |
 |
 |
 |
 |
| MO Number | Energy of MO hatrees | Description of Orbital |
|---|---|---|
| 89 | -0.297 | There is lots of bonding character in this MO from the in phase Px orbtials on each of the Br atoms. This orbital shows the bonding between the Mg and Br molecules. However it does not demonstrate a dative convalent bond as such. Whilst Gaussian is able to calculate where the areas of electron density lie (the bonding and anti bonding orbtials) it cannot show the origins of the density (i.e. which atom it comes from.) |
| 90 | -0.296 | This MO shows the Pz orbtials on each of the Br molecules in a bonding environment. There is very little interaction with the rest of the molecule. This is a sigma bond between the end on Pz orbitals. |
| 91 | -0.283 | The Px anti bonding orbtial is seen here. The interaction between the Px orbtials on each of the Br atoms is shown. This is a pi interaction. There is no bonding with other areas of the molecule shown. |
| 92 | -0.266 | The Py orbtials are shown in a bonding environment in this molecular orbtial. there is a pi interaction between the 2 Br Py orbtials. There is no interaction with the rest of the molecule. |
| 93 | -0.260 | The Pz anti bonding orbtials are shown in this MO. There is no interaction with other areas of the molecule. |
| 94 | -0.256 | The Py anti bonding orbitals are shown in this MO. There is no interaction with other areas of the molcule. |
| 95 | -0.209 | Small Pz orbtials are shown in this MO. This may reresent the anti bonding interaction with the Mg atoms by the Pz orbtials. The Pz orbtials in this representation are much samller than in MO90 and MO93, this represents the reduced electron density on the Br atom which could be a result of sharing the electron density with the Mg atoms. |
| 96 | -0.203 | There is a proportion of Px anti bonding charactoer in this orbital. Similarly to the MO95 the Px orbtials are evry small which may represent some sharing o electron density with the Mg (these are the anti bonding parts of the bond). |
| 97 | 0.013 | This MO represents the LUMO of the molecule. As was suggested in the study of the BH3 MOs, gaussian is not as good at computing unoccupied orbitals as it is at computing occupied orbtials. This means that this orbtial may be an inaccurate representation of the LUMO of the molecule. |
|

Does the position of the R groups (organic groups) and the ligands (solvent) make a dfference to the properties of the moelcule?[2]
The next question I am posing is if the position of the solvant molecules and organic ligands changes the physical properties of the molecules (i.e. the frequency of bond vibrations and the energie of the molecules). In order to answer this quesiton I have suggested three different isomers of the dimer to investigate.
 |
 |
 |
As can be seen from the table of geometries there is very little differecne in the bodn lengths for the moelcules 1,2 and 3. This shows that the conformation of the molecule and the position of the R group and solvant ligand have no significant effect on the length of the bonds in the molecule. The computed data agrees well with literature data from similar molecules. (Mg-O: 2.03A, Mg-C: 2.13A). ONe interesting observation of the data was that in the molecule 2 where one 'end' of the dimer has both R ligands and one end has both solvant ligands the Br-Mg bridging bonds were not the same legth. There was one set of 'short' bonds (2.65A, 2.64A)and one set of 'long' bonds (2.76A, 2.80A). The shorter bonds were on the THF end. Their shorter length may be a result of stronger bonds. The O on the THF has 2 lone pairs. These lone pairs may donate towards the Mg and result in the Mg being less electron deficicent and therefore able to create stonrger bonds with the Br(less dependant on the dative covalnet donation form the Br). This effect may also be the reason why the Mg-O bonds and the Mg-C bonds are shorter and longer respectivly than the similar bonds in molecules 1 and 3. The MgO electron density might donate towards the Mg somwhat and allow stronger (and therefore shorter) bonds to be formed from this Mg centre. And the lack of any O lone pair electron density at the other end of the molecule causes the bonds to be less electron dense and therefore weaker and longer.
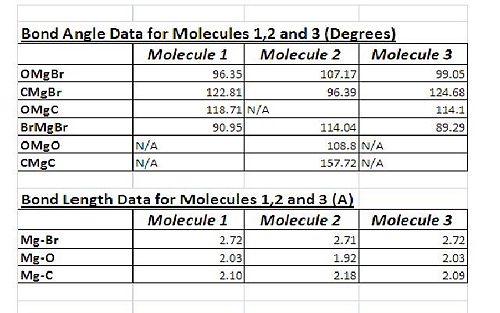
The Bond angles also compare well to data from literature[3]. (Br-Mg-C: 125degrees, O-Mg-O: 96.4degrees, C-Mg-C: 140.2degrees). We find that the data for molecule 1 and 3 is quite similar, for molecule 2 we find slightly different results. This variation is due to the changes in bond length. In order for the shorter Mg-Br bond to exist on the THF end of the molecule 2 the bond angle OMgBr must increase. Similarly for the CH3 end of the molecule, the longer bonds here must be accounted for by a reduced bond angle of C-Mg-Br. As a result of these effects the Br Bond angle becomes wider also in order to keep the Br bridge far enough formt he plane of the rest of the atoms to avoid steric repulsions.
| Energy (Hatrees) | |
|---|---|
| Molecule 1 | -572.93 |
| Molecule 2 | -572.87 |
| Molecule 3 | -572.93 |
The Molecule 2 is lowest in energy. The difference in energy (in KJ/mol) between molecules 1and2 is 1470.45, between 2 and 3 is 1379.54 and between molecule 1 and 3 90.90. As we can see form this data molecules 1 and 3 are actually very close in energy (a C-C bond is about 300KJ/mol so 90KJ/mol is negligable). The major differance in energy is that molecule 2 is a lot more stable than either 1 or 3. This is quite a large energy difference and is somewhat unexpected. The two THF groups have oxygen atoms which have 2 lone pairs each, it is expected intuitvily that these 2 groups would be least electronically unfavourbale as far apart as possible. This shows that the theoretical idea is not the real case.
From this study we can conclude that whilst the 2 solvent ligands (or equally the two R ligands) are on opposite ends of the molecule their arrangement has little effect on the geometry. Having both fo the solvent molecules (or R gorups) on one end howver does have a major effect on the geometry and the energy of the molecule.
IR investigation of Molecule 2
| Bond | Frequency of Vibration (cm-1) | Literature Value (cm-1) |
|---|---|---|
| Mg-Br | 112.32, 113.90 | 110 |
| Mg-C | 534.38 | 535 |



There is relatively good agreement here for the IR frequencies. It would be interesting as a further investigation to look at the difference in the vibrationas between molecules 1,2 and 3.
How will Gaussian represent an organic bridge?
In all the dimers investigated so far the bridge of the dimer has been a halide. It is also possible for dimers such as this to form organic bridges between metal atoms, though these are not favourable. This section will deal with the investigation of just how unfavourable the organic bridges are in comparision to the (isomeric) halide bridged dimers. The section will also investigate nhow Gaussian treats a organic bridge and whether it is able to compute this effectivly.

The energy was recorded as -571.67 hatrees which is a difference of 682.6KJ/mol. The data suggests that the organic bridge is actually more energetcially stable. This however is due to the calculation of the optimization of the moelcule. Gaussian has treated the organic groups in the bridge as if they were bonded to each other rather than both bonded to each Mg atom. We know (experimentally) that the organic bridge in the molecule is less stable. This therefore shows that Gaussian cannot be used to compute the organic bridge in this molecule.
Looking at the Geomtery I observed the following data:
| Bond | Comparable Bond in Mol.1 | Bond Length(A) | |
|---|---|---|---|
| Mg-CH2 | 2.78, 2.08 | Mg-Br | 2.72 |
| Mg-Br | 2.49 | Mg-CH3 | 2.10 |
| Mg-O | 2.02 | MgO | 2.03 |
| Angle | Comparable Angle in mol.1 | Angle(degrees) | |
|---|---|---|---|
| BrMgC | 127.02, 141.94 | CMgBr | 122.81 |
| OMgC | 112.09, 101.39 | BrMgO | 118.71 |
| CMgC | 34.95 | BrMgBr | 90.95 |
Fro the bond lengths there is some agreement, for exmaple ther Mg-O bond is a constant length. We must also bare in min dthat the Mg-CH2 and Mg-Br bonds aren't really that comparable as they are different atoms. One differnce we can observe though is that the organic bridge has 2 different bond lengths, unlike molecule 1 (which is its equivalent with a halide bridge). The reason for this is that Th Gaissain program returned the molecule with a bond between the two bridging carbon groups and treated the Mgs as if they were 3 coordinate instead of 4. I measured the C-C bond length witht he result of 1.61 (which is similar to a normal C-C bond length.
The angles in the molecule also show a little agreement.The BrMgC and CMgBr angles are very similar, which is not surprising as these are the same atoms. The major difference is the bon angle of the bridge itself. The C-Mg-C angle is very accute in comparison to the Br-Mg-Br angle. This, again, is due to the fact that the Gaussian calculation treated the Mg atoms as 3 coordinate and treated the Carbon gorups as if they were bonded (proabbly due to their proximity in the original molecule, as we have already seen that bonds in Gaussian are distance dependant).
In conclusion Gaussian does not treat the organic bridge as expected. This could be verified by using x-ray crystallography on the molecule practically to find the true geometry.
Further Investigations
Further investigations could include looking at how changing which halide is used to bridge effects the structure and also how changing the solvent or the R group effects it.
