Rep:Mod:Vic0313
Transition state and the Potential Energy Surface
Introduction
Figure 1. Transition state diagram1
- Transition state: corresponds to the point with maximum potential energy along the reaction coordinates. Therefore, the location of transition state along the reaction coordinate must be zero in gradient and positive in curvature with negative in second derivative value.1 In our optimisation and frequency calculations, the results of transition state are expected to show a negative imaginary frequency.
- For a real chemical system to undergo reactions, the reaction coordinate can be moving away from its equilibrium position in any degree of freedom, the potential energy can therefore be plotted against any one or a combination of these degrees of freedom or coordinates, known as Potential Energy Surface.
- Minimum: represents the lowest point on the potential energy surface along the reaction coordinate. Therefore, the corresponding gradient of the minimum should be zero with a negative curvature.
Optimisation and frequency calculations are carried out by methods described below 2 :
- HF/3-21G: A Hartree-Fock method of optimisation for the minimal basis set.
- Semi-empirical/PM6: A fitted method using experimental data to generate reasonable initial geometreis.
- B3LYP/6-31G: A more accurate method by Density Functional Theory (DFT) optimisation. This method taking the molecular orbitals into account to construct a more accurate higher basis set. This is used to optimize the initial geometries generated by the semi-empirical method.
Exercise 1: Diels-Alder reaction with butadiene and ethylene
In this exercise, transition state of reaction with butadiene and ethylene is obtained by semi-emperical/PM6 method. Orbital interactions as well as changes in bond distance are investigated to understand requirement of an allowed chemical reaction.
Molecular orbital analysis
Figure 2. MO diagram of Normal demand Diels-Alder reaction 3,4,5
The MO diagram above illustrates the expected orbital interaction for a Diels-Alder reaction with butadiene and ethylene. 3,4,5 Only the orbitals that are both symmetric or antisymmetric are capable to interact. Since the HOMO of butadiene and LUMO of ethylene are both antisymmetric and they obey the normal electron demand of Diels-Alder reaction (electron rich diene and electron poor dienophile), they are likely to interact strongly and hence result in the HOMO and LUMO of transition state. Whereas the LUMO of butadiene and HOMO of ethylene are further away in energy and therefore they are expected to interact weakly.
(Fv611 (talk) 13:03, 6 March 2017 (UTC) You haven't shown the interactions between symmetric orbitals, and you have switched around the bonding and antibonding MOs resulting from the combination of the asymmetric orbitals. Also the lowest energy MO for butadiene is drawn wrong.)
- Table of HOMO and LUMO
| Ethylene | Butadiene | Transition state | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| HOMO |
|
|
| |||||||||
| LUMO |
|
|
|
As shown above, the HOMO and LUMO of the transition state is arose by the interaction of the LUMO of butadiene and the HOMO of ethylene, which is not agreed with the MO diagram prediction for a normal demand Diels-Alder reaction above. This phenomena can be understood by large energy gap between the HOMO of butadiene and LUMO of ethylene is too large and therefore the transition state is dominated by interaction of butadiene LUMO and ethylene HOMO.
(Fv611 (talk) 13:03, 6 March 2017 (UTC) Not only you have not included the HOMO-1 and LUMO+1 orbitals for the transition state, you realised that your HOMO and LUMO didn't match the diagram you drew. You should have drawn it again with the help of the orbitals you computed.) It is clearly shown that the interacting molecular orbitals are both symmetric, and the interaction of symmetric-asymmetric molecular orbitals will be forbidden. This can lead to conclusion that an allowed chemical reaction will have symmetric-symmetric or antisymmetric-antisymmetric interactions with non-zero orbital overlap integral The reaction of symmetric-antisymmetric interaction with zero orbital overlap is expected to be forbidden.
Change in C-C bond lengths
- Table of typical C-C bond length 6
| C-C single bond | C=C double bond | Van der Waals radius of carbon | |
|---|---|---|---|
| Bond length (Å) | 1.54 | 1.47 | 1.7 |
- Bond distance of reactants and product
| Bond length (Å) | C1-C2 | C5-C6 | C3-C4 | C4-C5 | C2-C3 | C1-C6 |
|---|---|---|---|---|---|---|
| Butadiene | 1.33343 | 1.33343 | / | / | / | 1.47078 |
| Ethylene | / | / | 1.32754 | / | / | / |
| Product | 1.50030 | 1.50031 | 1.54070 | 1.53997 | 1.53995 | 1.33761 |
(Fv611 (talk) 13:03, 6 March 2017 (UTC) You were asked to compute the bond distances at the TS - it would have helped you provide a more complete discussion of the variation of internuclear distances.)
Carbon assignment |
During the reaction, the bond length of both double bonds (C1-C2, C5-C6, C3-C4) increase and the product corresponding bong length confirm this decrease in bond order from double bond to single bond with a longer bond length in the product. This is consistent with our expected mechanism. Formation of new carbon-carbon single bonds (C2-C3, C4-C5) is confirmed with the bond length in product with 1.53997 and 1.53995 Å respectively. This value is close to the single C-C bond value shown above. And the formation of new double bond at C1-C6 can be visualize through the change in bond length from 1.47078 to 1.33761 Å.
- Variation of internuclear distance from product to reactant
As shown above, bond distance between original doubly bonding C3-C4, C1-C2 and C5-C6 is decreasing slightly from product to reactant which is consistent with the expected bond order variation from single bond (product) to double bond (reactant). And the internuclear distance of C4-C5 and C2-C3 is decreasing hugely from reactant to product to prove the formation of new carbon bonds.
As we can see from the plot above, the bonding distance variation of C4-C5 and C2-C3 is synchronous and they map onto each other in the plot above. This demonstrates that the formation of two bonds happens synchronously. Therefore, the Diels-Alder reaction is known as a concerted cycloaddition.
- Vibration at transition state
Vibration at transition state |
Vibration at transition state is shown above at frequency equals - 948.79 cm-1. This negative frequency is known as the imaginary frequency correspond to the vibration at transition state. This also shows a synchronous and symmetric vibration at transition state.
Exercise 2: Regioselectivity of Diels-Alder Reaction with Cyclohexadiene and 1,3-Dioxole
In this exercise, transition states of a [4+2] cycloaddition with 1,3-dioxole and cyclohexadiene to yield endo and exo products respectively are investigated using the more accurate "B3LYP/6-31(G)" method by Density Functional Theory (DFT) to optimize the initial geometries generated by the "semi-emperical/PM6" method. Analysis of the corresponding molecular orbitals and relative energy levels can determine reaction barriers and reaction energies and thus understand the regioselectivity of this Diels Alder reaction.
Molecular Orbital analysis
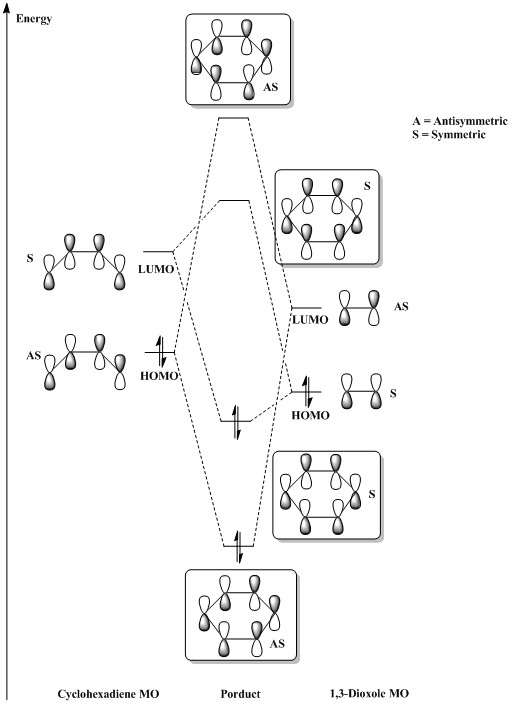
An inverse electron demand is expected for this Diels-Alder reaction due to the electron donating effect of two oxygen on dienophile (i.e. 1,3-dioxole) raises the energy of its HOMO sufficiently to interact with the LUMO of diene (cyclohexadiene). 3,4,5 The Molecular Orbitals of transition states confirm this expected results.
- Table of HOMO and LUMO involved in the formation of endo and exo transition states
| HOMO | LUMO | |||||||
|---|---|---|---|---|---|---|---|---|
| Endo |
|
| ||||||
| Exo |
|
| ||||||
| Cyclohexadiene |
|
| ||||||
| 1,3-Dioxole |
|
|
As shown in the table above, HOMO and LUMO formations of the transition states for both products are dominate by interaction of LUMO of cyclohexadiene and HOMO of 1,3-dioxole. Both the occupied and unoccupied orbitals associated with this reaction for both transition states have a plane of symmetry since they arose by the symmetric-symmetric (LUMO of diene and HOMO of dienophile) orbital interactions.
- Molecular Diagram of Inverse Demand Diels-Alder reaction
(Be careful, you've done this earlier - the diene and dienophile are not in the same plane. Attack occurs from above or below Tam10 (talk) 12:32, 8 March 2017 (UTC))
Figure 3. Inverse Demand MO diagram 3,4,5
Activation energies and reaction energies
- Summary of computed datas
| Cyclohexadiene | 1,3-Dioxole | Endo T.S. | Endo Product | Exo T.S. | Exo Product | |
|---|---|---|---|---|---|---|
| The Gibbs free energy (kJ/mol) | -612505.404377 | -701106.655215 | -1313505.33826 | -1313741.43111 | -1313499.44139 | -1313738.74523 |
Activation energy (Eact)= energy of transition state - sum of reactant energies;
Reaction energy = energy of product - sum of reactant energies;
For Endo product:
Eact = -1313505.33826 - (-612505.404377 - 701106.655215) = + 106.72 kJ/mol
Reaction energy = E = -1313741.43111 - (-612505.404377 - 701106.655215) = - 129.37 kJ/mol
For Exo product:
Eact = -1313499.44139 - (-612505.404377 - 701106.655215) = + 112.62 kJ/mol
Reaction energy = E = -1313738.74523 - (-612505.404377 - 701106.655215) = - 126.69 kJ/mol
- Summary of reaction barriers and reaction energies
| Endo | Exo | |
|---|---|---|
| Activation energy (Eact) (kJ/mol) | + 106.72 | + 112.62 |
| Reaction energy (kJ/mol) | - 129.37 | - 126.69 |
Calculations above demonstrate that formation of the endo transition state requires a lower activation energy, therefore the endo product is considered to be kinetically favourable. This observation can be explained by the stabilising interaction between the oxygen lone pairs on 1, 3-dioxole and the developing π bond on cyclohexadiene below the plane of the oxygen orbitals.
In terms of thermodynamic products, the exo product is expected to be thermodynamically favourable due to less steric hindrance occurring during the exo transition state. However, according to the calculated value, the thermodynamic product is the endo product. This can be understood by effect of secondary orbital interaction arise between the new π orbitals on the cyclohexadiene and the 1, 3-dioxole oxygen lone pairs that are locating below the plane of cyclohexadiene for the endo product whereas the exo product has only primary orbital interactions.
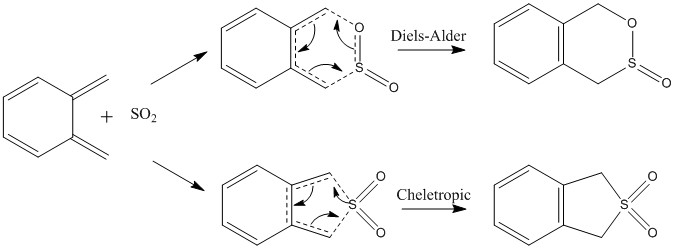
Exercise 3: Xylyene-SO2 Cycloaddition
There are three possible reaction pathways for cycloaddition reaction of xylyene and sulfur dioxide to occur including Diels-Alder Endo, Diels-Alder Exo and Cheletropic reaction. In this exercise, investigations of the transition states and relative energy levels are carried out to determine the most likely reaction route for this cycloaddition reaction.
Pathway analysis
- Reaction pathways and corresponding products
| Reaction pathway | Product | Vibration at imaginary frequency | IRC | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Diels-Alder Endo |
|
|
| |||||||||
| Diels-Alder Exo |
|
|
| |||||||||
| Cheletropic |
|
|
|
As shown above, the computational IRC illustrates the process of bond formation during the reaction. During the sigma bond formation of the cycloaddition reaction, bonding of the 6-membered ring becomes delocalized with 6 electrons, and thus becomes aromatic.
For the Diels-Alder reaction, both pathway (Endo or Exo) shows the same order of bond formation that the C-O bond forms first follow by the C-S bond. However, during the cheletropic reaction, bond formation is synchronous. Reasons for this synchronization of cheletropic reaction and asynchronization of Diels-Alder reaction can be due to the size difference of oxygen and sulfur atom. Since oxygen is smaller in size with similar size as the carbon atom, the interaction of C-O pair is expected to be higher due to better orbital overlap, and thus lead to faster C-O bond formation.
Energy calculations and analysis
(The IRCs from the calculations shouldn't be plotted together. Their TSs should at least be at IRC=0. In reality, they do not share the same coordinate. The relative energies of the stationary points can be legitimately compared however Tam10 (talk) 12:32, 8 March 2017 (UTC))
Figure 4. Change in energy for three reaction pathway
- Summary of computed datas
| Energy (kJ/mol) | Reactant (diene) | Reactant (dienophile) | Transition state | Product |
|---|---|---|---|---|
| Diels-Alder Endo | 573.692798 | -239.0097852 | 359.123794 | 175.91639 |
| Diels-Alder Exo | 573.692798 | -239.0097852 | 363.366602 | 173.369655 |
| Cheletropic | 573.692789 | -239.0097852 | 383.323029 | 114.440303 |
(You have taken the wrong values for the thermochemistry. These are the sums of the electronic and thermal energies, not the electronic and thermal free energies Tam10 (talk) 12:32, 8 March 2017 (UTC))
For Diels-Alder Endo:
Eact = 359.123794 - (573.692798 - 239.00978752) = 24.44 kJ/mol
E = 175.91639 - (573.692798 - 239.00978752) = - 158.767 kJ/mol
For Diels-Alder Exo:
Eact = 363.366602 - (573.692798 - 239.00978752) = 28.68 kJ/mol
E = 173.369655 - (573.692798 - 239.00978752) = - 161.313 kJ/mol
For Cheletropic:
Eact = 383.323029 - (573.692798 - 239.00978752) = 48.64 kJ/mol
E = 114.440303 - (573.692798 - 239.00978752) = - 220.243 kJ/mol
- Summary of thermodynamic datas
| Energies (kJ/mol) | Reaction barrier | Reaction energies |
|---|---|---|
| Endo | 24.44 | -158.767 |
| Exo | 28.68 | -161.313 |
| Cheletropic | 48.64 | -220.243 |
According to the thermodynamic data calculated above, it is clear that the Diels-Alder Endo path has a lowest activation energy of only 24.44 kJ/mol, thus the Endo Diels-Alder product is most kinetically favourable. For cheletropic reaction, the reaction barrier is much larger than the Diels-Alder reaction. This can be due to unfavourable electron-electron replusion by the two oxygen atoms on the 1,3-dioxole during transition state Whereas for the Cheletropic product with highest reaction energy of -220 kJ/mol is considered to be the thermodynamic product. This can be due to formation of a less strained ring in cheletropic reaction compared to the highly strained Diels-Alder product.
Unfavourable Diels-Alder reaction with second cis-butadiene (diene) fragment
- Summary of computed datas
| Energy (kJ/mol) | Reactant (diene) | Reactant (dienophile) | Transition state | Product |
|---|---|---|---|---|
| Diels-Alder Endo | 573.692798 | -239.0097852 | 267.984805 | 172.259068 |
| Diels-Alder Exo | 573.692798 | -239.0097852 | 275.821924 | 176.706665 |
- Reaction barriers and reaction energy
| Energy (kJ/mol) | Reaction energy | Reaction barrier |
|---|---|---|
| Endo | 66.70 | 162.42 |
| Exo | 58.86 | 157.98 |
According to the calculations above, both reaction pathway require much higher activation energy than the previous Diels-Alder reaction path discussed above. Both reaction is kinetically unfavourable as well as thermodynamically unfavourable due to a positive value of reaction energies. (i.e. products are higher in energy than reactants.)
Conclusion
Use of computational techniques in Gaussian can predict the feasibility of a chemical reaction via transition state investigation as well as thermodynamic data calculations. This is a convenient and easy approach for chemist to determine possible outcomes without actual experimental work. Gaussian gives relatively accurate molecular orbitals via optimisation of the starting geometries and frequency calculations. Direct visualisation of molecular orbitals of the reactant fragments and transition state can be used to predict the dominant orbital interactions during the reaction process. Also, this method can show the reaction pathways for new bond formations via IRC studies, and thus visualize the synchronization of bond formations.
However, the tutorial and exercise calculations above exclude consideration of reaction conditions. For normal Diels-Alder reaction, certain temperature is required for a reaction to take place. Also, use of different methods in Gaussian basis sets (i.e. DFT or Semi-empericial) can lead to different results. As mentioned in the tutorial section, the “Semi-empirical/PM6” setting will give a wrong prediction of TS for Azide-Alkyne Huisgen Cycloaddition. Therefore, decision on which method to use should be considered carefully. Generally, the more complex method with higher basis sets will give a more accurate prediction of the outcomes, and which is time-consuming.
Reference
1. P. Atkin and J. Paula, Physical chemistry, 2006.
2. Quantum Mechanics 3, Calculation of Molecular Geometries, Prof M. Bearpark, Imperial College London, 2015.
3. Boger, Dale (1989). Progress in heterocyclic chemistry (1st ed.). New York: Pergamon.
4. Rooshenas, Parham; Hof, Kira; Schreiner, Peter R.; Williams, Craig M. (1 February 2011). "1,2,4-Triazine vs. 1,3- and 1,4-Oxazinones in Normal- and Inverse-Electron-Demand Hetero-Diels-Alder Reactions: Establishing a Status Quo by Computational Analysis". European Journal of Organic Chemistry. 2011 (5): 983–992.
5. Dang, Anh-Thu; Miller, David O.; Dawe, Louise N.; Bodwell, Graham J. (1 January 2008). "Electron-Deficient Dienes. 5. An Inverse-Electron-Demand Diels−Alder Approach to 2-Substituted 4-Methoxyxanthones and 3,4-Dimethoxyxanthones". Organic Letters. 10 (2): 233–236.
6. Fox, Marye Anne; Whitesell, James K. (1995). Organische Chemie: Grundlagen, Mechanismen, Bioorganische Anwendungen. Springer.