Rep:Mod:VR1994

Introduction

This computational study is based on the characterisation of transition structures on potential energy surfaces for two different types of reactions, the Cope Rearrangement and several Diels-Alder cycloaddition reactions. In particular, the Cope Rearrangement reaction of 1,5-hexadiene, the Diels-Alder cycloaddition of ethene and s-cis-1,2-butadiene and, finally, the Diels-Alder cycloaddition of cyclohexa-1,3-diene and maleic anhydride via both the endo and exo transition states. It is now well known that the transition state corresponds to the largest energy point (i.e. a maximum in energy) in the reaction coordinate and so these species can not be isolated as it is a transient species that immediately reverts back to the reactants or goes on to form the products. As a result of the fleeting existence of the transition state, the only method that one could use to be able to locate and study the transition state is to use computational chemistry i.e. via calculations using the Gaussview Program. There is a great interest in studying the transition state as it provides much chemical information that form the basis for any chemical reaction such as the activation energy, and thus the rates of reactions, as well as providing information on reaction mechanisms.

In this study, the method of using the Gaussview program to locate the transition states was adopted by the use of three main calculation methods: Hartree-Fock/321-G, B3LYP/6-31G(d) (Density Functional Theory) and Semi-Empirical/AM1 levels of theory.

In summary, these methods involved two different processes to optimize the structure of the transition state. The first of which involved the guessing of a transition structure and optimizing this guess using the TS (Berny) optimization method. The second method involves the use of the QST2 optimization method in which the all the atoms in the reactants and products were labelled and the subsequent calculation provided the transition structure via interpolation between the input reactant and product structures; this worked by finding a maxima in energy between these structures on the potential energy surface.

Nf710 (talk) 11:22, 4 December 2015 (UTC) Nice well rounded intro

The Cope Rearrangement of 1,5-hexadiene

Background

The reaction scheme for the Cope Rearrangement of 1,5-hexadiene is provided in Figure 1 below. The Cope Rearrangement is a [3,3]-sigmatropic rearrangement, which is a pericyclic reaction in which one sigma bond is broken whilst another sigma bond is formed. According to the Woodward-Hoffman rules, the Cope Rearrangement is a thermally allowed reaction ,as the total number of components that fit the equation (4q + 2)_s + (4r)_a is odd, since there are two _π2_a components and one _σ2_s component.

The mechanism of the Cope Rearrangement has widely been studied to understand whether the mechanism proceeds via a concerted or a non-concerted process. However, the modern opinion is in accord with the former mechanism process, a concerted mechanism. From the concerted mechanism, the Cope Rearrangement occurs via both a boat and a chair conformations of the transition state. In the following calculations, the local minima, associated with the reactants and products, as well as the maxima, corresponding to the transition states, were located and analysed for this Cope Rearrangement. All the calculations were carried at out the Hartree-Fock and Density Functional Theory levels of theory with the aim of attaining the activation energies of the Cope Rearrangement when the reaction proceeded via a boat or a chair transition state conformation.

Fig.1 The Cope Rearrangement of 1,5-hexadiene.

Nf710 (talk) 11:23, 4 December 2015 (UTC) Really good understanding of the chemistry

Hartree-Fock and Density Functional Theory comparisons

Before commencing the calculations for locating the transition states for the Cope Rearrangement it is important to discuss the theoretical points behind the HF and DFT levels of theory. The Density Functional Theory method uses far fewer approximations in its calculations which leads to more accurate results and energy values that are closer to the true value being given. HF tends to give values in energy that are far higher than the true value. The Hartree-Fock and DFT calculations have a lot in common as the equations must be solved self-consistently. The Hartree-Fock method focuses on wavefunctions and orbitals, in particular it concentrates on the Slater Determinant. However, DFT equations concentrate on electron densities and as it includes an approximate treatment of electron correlation, it produces more accurate results than the Hartree-Fock theory. In the Hartree-Fock theory, the movement of the electrons are described by MO theory i.e. a linear combination of atomic orbitals. Hartree-Fock does not produce exact results as the theory is a significant approximation to the Schrödinger equation. This approximation is that the electrons, at all times, feel an average negative Coulomb energy when interacting with other electrons. Whilst this approximation simplifies matters, it leads to inaccurate results being presented. In cases where this approximation leads to severe errors, the Density Functional Theory is used to help overcome any issues by accounting for electron correlation, which is the potential that electrons experience, in the equations. A significant drawback of the DFT calculations is that it cannot be improved upon and thus more accurate results cannot be achieved.

Nf710 (talk) 11:34, 4 December 2015 (UTC) very nice understanding of the methods, HF does not account for electron correlation because electrons of opposite spin can be in the same place at the same time in one spatial orbital which is wrong and there for the repulsion term is incorrect.

Optimising the Reactants and Products

In the following section, various conformers of 1,5-hexadiene will be studied. There is a possibility of many different conformers due to the ability of 1,5-hexadiene to be able to freely rotate about it's central C-C single bond.

Optimising the conformers of 1,5-hexadiene using the HF/3-21G level of theory

To begin, a molecule of 1,5-hexadiene was prepared on the Gaussview program. This structure was then optimised at the HF/3-21G level of theory to give many different conformers, namely the anti1, anti2 and gauche3 conformers shown below (in the Jmol structures). Below, the energies and point groups (which was provided via the symmetrize tool on Gaussview) of the conformers are given.

Conformer	Jmol structure	Energy (hartrees)	Calculation Summary	Point Group	Point Group Summary
anti1		-231.69260236		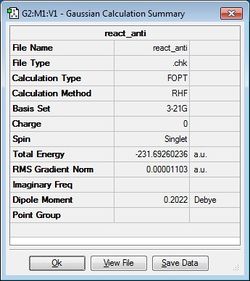C2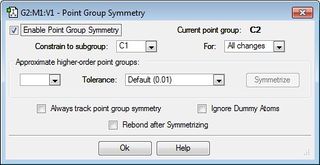
gauche3		-231.69266121		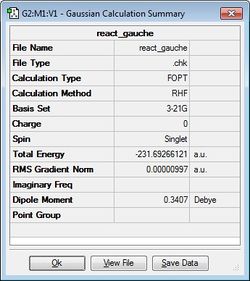C1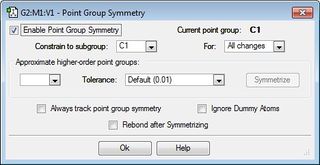
anti2		-231.69253517		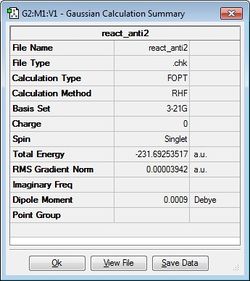Ci

Firstly, the 1,5-hexadiene molecule was altered to ensure an "anti" linkage was formed with an anti-periplanar geometry (i.e. the dihedral angle is 180°), was formed. This structure was then optimised at the HF/3-21G level of theory to provide the anti1 and anti2 conformers via separate calculations. It can be seen that the energies and point groups of both of these conformers agree with the data provided in the appendix in the laboratory script. It can also be seen that the anti1 conformer is slightly more stable (i.e. lower in energy) than the anti2 conformer.

Next, the initial 1,5-hexadiene molecule was altered to provide a gauche linkage for the central four carbon atoms (i.e. the dihedral angle is 60°) and again it was optimised using the HF/3-21G level of theory to give the gauche3 conformer.

The expectation is that the anti1 and anti2 conformers would be lower in energy than gauch3 conformers as there are no steric clashes or interactions as the alkenyl groups attached to C3 and C4 are 180° apart in anti1 and anti2 conformers whilst only 60° apart in gauche3 leading to greater steric interactions. The greater the angle between the alkenyl groups, the less the steric repulsion between the groups. However, as can be seen from the table above, the gauche3 conformer has the lowest energy geometry which contradicts the initial expectation. The global minimum is in fact the gauche3 conformer as there a favourable interaction possible between the bonding π orbital of one alkenyl group and the vinyl proton of the other alkenyl group which lowers the total energy ; in this case, there is a weak form of hydrogen bonding between the softly acidic vinyl C-H bond and the soft π bonding orbital (basic) .

Nf710 (talk) 11:58, 4 December 2015 (UTC) interesting theory you are correct but that study is pretty old if you had looked in the orbitaks you should be able to see the twist of the gauche leads to favourable inphase overlap between the pi systems.

Optimising the anti2 conformer of 1,5-hexadiene using the B3LYP/6-31G(d) level of theory

Next, the anti2 conformer was further optimised at the B3LYP/6-31G(d) level to give a reactant with the energy and Jmol structure given below.

Energy (hartrees)	Calculation Summary	Jmol structure
-234.61171062

After re-optimising at the B3LYP/6-31G(d) level, the point group of the anti2 conformer remains the same, i.e. C_i, which can be seen in Fig. 2 below.

Fig. 2 The point group summary of the anti2 conformer of 1,5-hexadiene when using the 6-31G(d) level of theory

Comparison of the anti2 conformer of 1,5-hexadiene when using the HF/3-21G and B3LYP/6-31G(d) levels of theory

Whilst the energy of the anti2 conformer cannot strictly be compared between the two levels of theory, the difference in geometries can be discussed. Below the difference in bond lengths and dihedral angles are discussed.

Bond Lengths

Fig. 3 The numbering of the carbon atoms in the anti2 conformer of 1,5-hexadiene corresponding to the bond lengths given below.

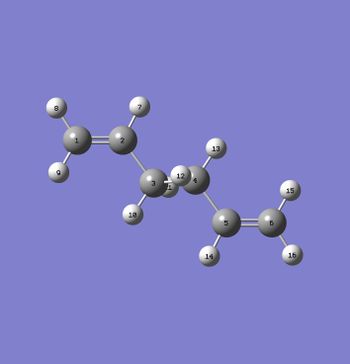
The anti2 conformer was labelled as depicted in Fig. 3 and these labels are used to provide the bond lengths given in the table below.

	Bond Lengths (Å)
Atoms	HF/3-21G	B2LYP/6-31G(d)
C1-C2	1.31615	1.33350
C2-C3	1.50895	1.50420
C3-C4	1.55264	1.54816

Immediately, it can be seen that the HF level of theory gives a slightly shorter C1-C2 bond length (i.e. a C=C alkene bond) than B3LYP. The literature value of the C1-C2 bond length is 1.340 Å ; thus, one can see that the B3LYP level of theory is much more accurate in reproducing C1-C2 alkene bond length in 1,5-hexadiene. The literature value of the C2-C3 bond length is 1.508 Å and that of C3-C4 is 1.538 Å . So it can be seen that the HF level of theory is better at reproducing the C2-C3 bond length whilst B3LYP is better at reproducing the C3-C4 bond length. Overall, the B3LYP level of theory is better at reproducing a structure more accurately as it uses fewer approximations in it's calculations.

Dihedral angles

The dihedral angles of the anti2 conformer are given below when using the different levels of theory.

	Dihedral Angle (°)
Atoms	HF/3-21G	B3LYP/6-31G(d)
C1-C2-C3-C4	114.65912	118.59923
C2-C3-C4-C5	179.99940	180.00000

Initially, the dihedral angle (i.e. between C2-C3-C4-C5) was set to 180° and so the fact that the dihedral angle had been altered from 180° to 179.99940° shows the inconvenience when using the Hartree-Fock level of theory. This is further backed up by examining the angle between the carbons C1-C2-C3-C4. One would expect that at an alkene centre, there is a trigonal planar arrangement and so the dihedral angle should be 120°. However, the Hartree-Fock level of theory deviates from this expected trigonal planar by more than the B3LYP level of theory suggesting the greater appropriateness in using the B3LYP level of theory in order to produce accurate dihedral angles.

Frequency analysis of the anti2 conformer of 1,5-hexadiene

Next, a frequency analysis was conducted on the anti2 conformer using a B3LYP/6-31G(d) calculation and the calculation summary is provided below (Fig. 4).

Fig. 4 The calculation summary of the anti2 conformer of 1,5-hexadiene when performing a frequency analysis.

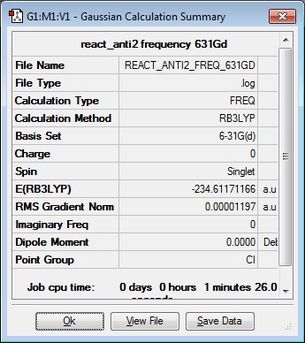
All vibrational frequencies, as can be seen from the IR spectra below (Fig. 5), are positive and real and so confirms that a minimum has been reached for the anti2 conformer. The absence of imaginary frequencies confirms that a minimum is reached and the calculation didn't result in a structure that corresponded to a transition state (i.e. an energy maximum). This frequency calculation corresponds to the second derivative of the potential energy; a negative second derivative (maximum i.e. transition states) would lead to the presence of imaginary frequencies whilst a positive second derivative (minimum) would provide positive vibrational frequencies.

Nf710 (talk) 12:06, 4 December 2015 (UTC) This is true but you could have proved with the quantum harmonic oscilator equation

Fig. 5 The IR spectrum of the anti2 conformer of 1,5-hexadiene obtained using a frequency analysis with the 6-31G(d) level of theory.

Thermochemical properties of the anti2 conformer of 1,5-hexadiene

The thermochemical properties gained from performing a frequency analysis on the anti2 conformer are listed below.

	Calculation at 298 K (Hartrees)	Calculation at 0 K (Hartrees)
Sum of Electronic and Zero-Point Energies	-234.469215	-234.469215
Sum of Electronic and Thermal Energies	-234.461867	-234.469215
Sum of Electronic and Thermal Enthalpies	-234.460922	-234.469215
Sum of Electronic and Thermal Free Energies	-234.500800	-234.469215

Optimisation of the "Chair" and "Boat" Transition Structures

Having now optimised the anti2 conformer of 1,5-hexadiene and subsequently performing a frequency analysis, it is now appropriate to discuss the "Chair" and "Boat" transition structures in further detail to allow us to determine which reaction pathway gives lowest activation energy for the Cope Rearrangement.

Optimising the allyl fragment

Prior to analysing the transition structures, an allyl fragment must be drawn and optimised using the HF/3-21G level of theory. One needs two allyl fragments to be able to construct both the "chair" and "boat" transition structures. Below, the results are shown when the allyl fragment was optimised.

Jmol structure	Calculation Summary

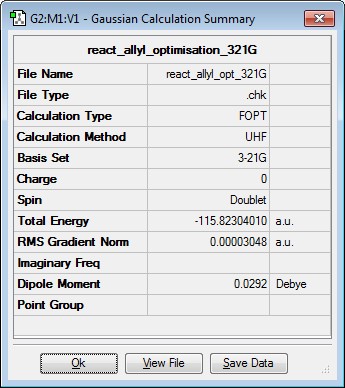N.B. the point group of the allyl fragment was C_2v after optimisation.

Optimising the "Chair" Transition Structure

Using the HF/3-21G level of theory

Using the optimised allyl fragment, the "chair" transition structure was guessed by placing two allyl fragments 2.2 Å (i.e. the separation of the terminal carbons are 2.2 Å) apart in a staggered conformation. This guess structure was optimised to a transition state structure by optimising to a TS(Berny). The summary of the results are provided below.

Jmol structure	Calculation Summary

The calculation had converged and so the "chair" transition structure had successfully been computed. Thus, it is now possible to attain the imaginary frequency corresponding to the Cope Rearrangement. The imaginary frequency, -817.94 cm^-1, is shown below.

Vibration that leads to a reaction

The presence of the imaginary frequency confirms that the structure calculated is present at a maximum in energy and hence corresponds to the "chair" transition structure. An imaginary frequency represents a negative second derivative of the potential energy surface and so corresponds to a maximum in energy and thus a transition state structure. A transition structure only has one imaginary frequency. An imaginary frequency comes about due to a negative second derivative and it corresponds to a negative force constant i.e. a transition state. A negative second derivative means that the energy decreases in directions away from the point under consideration and thus it shows it is a maximum. The negative force constant gives rise to an imaginary frequency as the vibrational frequency depends on the square root of the force constant.

$v=\frac{1}{2\pi }\sqrt{\frac{k}{m}}$

k is the force constant. The square root of a negative number gives rise to an imaginary solution and hence an imaginary vibration.

Nf710 (talk) 12:07, 4 December 2015 (UTC) apologies for above I see you have clearly explained it here

Using the Frozen Coordinate Method

The optimised allyl fragment can also be used to produce a "chair" transition state by using the Frozen Coordinate Method. In this case, the optimised allyl fragments are again placed 2.2 Å (i.e. the separation of the terminal carbons are 2.2 Å) apart in a staggered conformation. The distance between each set of terminal carbon atoms on the allyl fragments are frozen to 2.2 Å whilst the rest of the molecule to move. An optimisation is subsequently carried out at an HF/3-21G level of theory. Following this, the bond breaking and bond forming distances were optimised, using the HF/3-21G level of theory, further to produce the final transition state structure shown below. This was also a successful method in producing the "chair" transition state structure.

Jmol structure	Calculation Summary

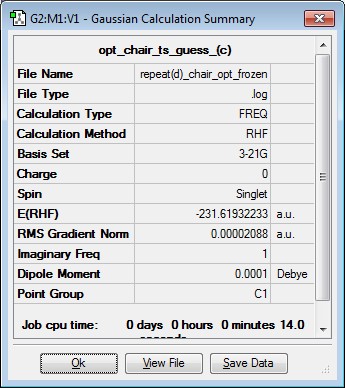Once again, a single imaginary frequency is produced with a frequency of -817.89 cm^-1. The vibration below leads to the Cope Rearrangement.

Vibration that leads to a reaction

Comparison of the "Chair" transition structures using the guessed transition structure method and the Frozen Coordinate Method

Below, a comparison of the bond breaking and bond forming distances of the "chair" transition structure using the guessed structure and Frozen Coordinate methods are given below.

	Bond forming length (Å)	Bond forming length (Å)
T.S structure from guess method	1.38928	2.02009
T.S. structure from Frozen coordinate method	1.38929	2.02070

Whilst the bond forming bond lengths are virtually exact when using either method, there is a small difference in the bond breaking lengths. The Frozen Coordinate method produced a bond breaking length which is slightly larger but the difference is not insignificant and thus very similar transition state structures have been produced by both methods.

Optimising the "Boat" Transition Structure

Now, the "boat" transition structure will be optimised.

Using the QST2 method

The boat transition structure was optimised using the QST2 method using the HF/3-21G level of theory. This method works by interpolating between the reactant and product structures and in this process, it is expected that an energy maxima will be reached corresponding to the transition structure.

Initially, the anti2 conformer was used as the starting point to generate the "boat" transition structure using the labelling provided in Fig. 6.

Fig. 6 Numbering used for the initial conformer of 1,5-hexadiene.

However, optimising the anti2 conformer using a QST2 calculation provided an error resulting in the transition structure shown below (Fig. 7). This is extremely unfavorable as the reactant and product geometries are too different from the transition structure geometry and so they are not able to form the transition structure. The calculation failed as it did not produce the transition structure that was required.

Fig. 7 Transition state observed using the conformer above.

Therefore, instead of using the anti2 conformer, the (imaginary) conformer shown below (Fig. 8) was used instead as it provided the reactants and products with a geometry that closely resembled the boat transition structure. The atoms were labelled as according to Fig. 8. In order to have a successful QST2 calculation, the reactants and products must share a similar geometry to the transition structure we are after i.e. the "boat" transition structure.

Fig. 8 The numbering of the conformer required to produce the correct Transition Structure.

Nf710 (talk) 12:10, 4 December 2015 (UTC) All your frequcenies for this part are correct well done.

The conformer above (Fig. 8) was then optimised using the QST2 calculation at the HF/3-21G level to produce the boat transition structure; the results are provided below.

Jmol structure	Calculation Summary

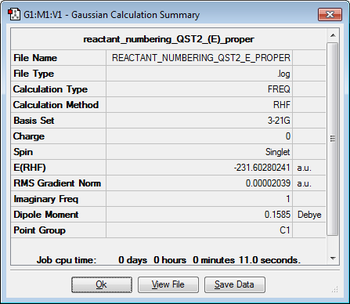Once again, a single imaginary frequency, of -839.90^-1, was produced which corresponds to a transition structure. The vibration shown below corresponds to the vibration that leads to the Cope Rearrangement.

Vibration that leads to a reaction

Intrinsic Reaction Coordinate (IRC) analysis

Now the optimized "chair" transition structure will be analysed by the Intrinsic Reaction Coordinate calculation using the HF/3-21G level of theory. The point of the IRC calculation is provide information regarding which conformers are connected to the chair and boat transition structures. The IRC calculation had converged after sampling 44 points along the IRC even though a sampling of 50 points was initially specified in the calculation input. It must be stated that the calculation needs only to be run in the forward direction as the reaction coordinate is symmetrical. The accuracy of an IRC calculation can be improved by increasing the number of points to be sampled along the IRC coordinate but 50 points was found to be enough in order to allow a convergence of the calculation. The results from the IRC calculation are provided below.

Fig. 9 Total Energy IRC of the optimised "chair" transition structure.
Fig. 10 RMS Gradient Norm along the IRC for the optimised "chair" transition structure.

From the results of the IRC calculation, it can be seen that the RMS gradient (i.e. derivative of the total energy along the IRC) approaches and becomes zero with increasing IRC which confirms that calculation has been completed and has converged. N.B. the IRC calculation must be run at the same level of theory as that used when optimising the transition state structure (here, the HF/3-21G level was used consistently).

Nf710 (talk) 12:13, 4 December 2015 (UTC) Nice IRC but you havent connect the confs that it connects and therefor. you could have done this by computing force constants at every step and then comparing the final one to the appendix. or re optimised the final structure.

Activation Energies

In order to be able to calculate the activation energies of this Cope rearrangement via either transition structure, the previously optimised chair and boat transition structures must be reoptimised at the B3LYP/6-31G(d) level. This was done by optimising to a TS(Berny)(as was done when computing the chair transition structure from a guess structure) whilst completing a frequency analysis. Below the results of the boat and chair transition structures arising from the reoptimisations are shown.

Below, the calculation summary and the imaginary vibration, of frequency -530.36^-1, of the reoptimised boat structure is shown.

Imaginary frequency vibration	Calculation Summary

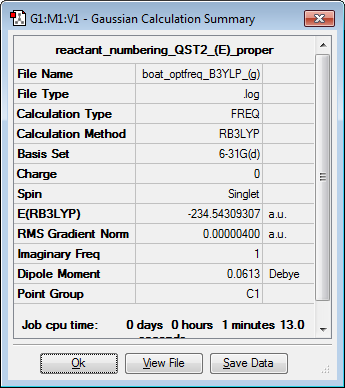Below, the calculation summary and the imaginary vibration, of frequency -566.36^-1, of the reoptimised chair structure is shown.

Imaginary frequency vibration	Calculation Summary

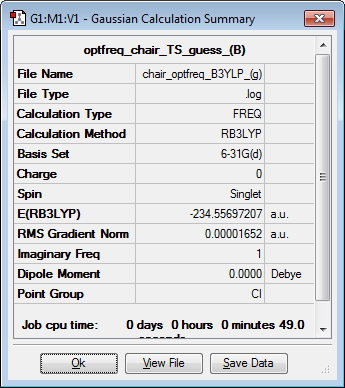Having now reoptimised the chair and boat transition structures, it is possible to calculate the activation energies for the reactant, in the anti2 conformation, to convert to the product via both the chair and boat transition structures when using the HF/3-21G and B3LYP/6-31G(d) levels of theory at both 0 K and 298.15 K. Before that, all the thermochemical data associated with the transition structures (both chair and boat) and the reactant, in the anti2 conformation, are provided below at HF/3-21G and B3LYP/6-31G(d) levels of theory used (and at 0 K and 298.15 K).

	HF/3-21G Electronic Energy (a.u.)	HF/3-21G Sum of Electronic and Thermal Energies at 0 K (a.u.)	HF/3-21G Sum of Electronic and Thermal Energies at 298.15 K (a.u.)	B3LYP/6-31G(d) Electronic Energy (a.u.)	B3LYP/6-31G(d) Sum of Electronic and Thermal Energies at 0 K (a.u.)	B3LYP/6-31G(d) Sum of Electronic and Thermal Energies at 298.15 K (a.u.)
Chair	-231.61932241	-231.466697	-231.461338	-234.55697207	-234.414894	-234.408976
Boat	-231.60280241	-231.450930	-231.445301	-234.54309307	-234.402342	-234.396008
Anti 2 Reactant	-231.69253517	-231.539539	-231.532565	-234.61171062	-234.469215	-234.461867

From this thermochemical data, the activation energies can be found and they have been listed in the table below.

	HF/3-21G		B3LYP/6-31G(d)		Expt.
	0 K	298.15 K	0 K	298.15 K	0 K
ΔE (Chair)(kcal/mol)	45.709011	44.695584	34.086916	33.189579	33.5 ± 0.5
ΔE (Boat)(kcal/mol)	55.602945	54.758945	41.963409	41.327115	44.7 ± 2.0

Much information can be gathered from this data. Firstly, the energy required to surmount the transition structure is greater at 0 K than at 298.15 K. This statement is rather straight forward as there is an absence of thermal energy at 0 K and so a greater energy input is required to surmount the activation barrier. The presence of thermal energy (E = kT) means that the activation barrier can be surmount much more easily as less energy must be input into the system. Furthermore, the accuracy of the activation energies that are obtained is much greater when using the B3LYP/6-31G(d) level of theory as it uses fewer approximations in its calculations. Lastly, our aim was to find out which transition structure provided a lower energy pathway for the Cope rearrangement. This can now be ascertained by observation of the activation energies above. It can clearly be seen that the activation energy for the Cope Rearrangement when passing through a chair transition structure is much lower than when passing through a boat transition structure. Thus one can conclude that the rate of the Cope Rearrangement is much greater when passing through the chair transition structure and so it is the preferred route for the reaction.

Nf710 (talk) 12:24, 4 December 2015 (UTC) Your energies are correct and you have come to correct conclusions. You didnt however say how the geoms are approximated well for the lower basis set. but energies or very off. therefore for geoms a lower basis set can be sufficient. This was an extremly well written report and you have done basically everything asked of you and you have backed it up with a very good understanding of the theory

The Diels-Alder cycloaddition

Background

Two different Diels-Alder reactions were studied in this study. Firstly, the Diels-Alder cycloaddition of ethene and cis-butadiene (Fig. 11) was studied in depth followed by the Diels-Alder cycloaddition of maleic anhydride and cyclohexa-1,3-diene (Fig. 12). Diels-Alder reactions are [4+2]-cycloadditions in which a diene and a dienophile react in a concerted pericyclic reaction. The Diels-Alder cycloadditions are thermodynamically favorable as two new σ bonds are much stronger than two π bonds. For the reaction to occur most effectively, there must be an electron rich diene and an electron deficient dienophile as this allows the HOMO and LUMO to be closer in energy and so allows greater orbital interactions. Thus it is expected that the reaction between maleic anhydride, an electron poor dienophile, and cyclohexa-1,3-diene, a relatively electron diene, should be more facile than that between cis-butadiene and ethene. In terms of the Woodward-Hoffmann rules, the Diels-Alder cycloaddition is a thermally allowed reaction. This is because the total number of components that fit the equation (4q + 2)_s +(4r)_a is odd. In this case there is one _π4₂ component and one _π2_s component. It is important to note that q and r can only take integer values and that the suffixes 'a' and 's' stand for antarafacial and suprafacial respectively . In all of the following calculations, semi-empirical/AM1 calculations will be carried out. There are many advantages of using this orbital method over using Hartree-Fock as the calculations converge more quickly and it is more applicable towards the organic molecules studied in these reactions. Moreover, the endo and exo transition states of the reaction between maleic anhydride and cyclohexa-1,3-diene will be studied which forms the endo and exo products shown below in Fig. 12. It should be noted that reactions between reactants in which the HOMO and LUMO are most closely matched in energy with the same symmetry will allow a reaction to occur.

Fig. 11 The Diels-Alder reaction between ethene and cis-butadiene.

Fig. 12 The Diels-Alder reaction between maleic anhydride and cyclohexa-1,3-diene to form the endo and exo products.

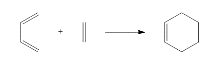
Before commencing the studies on the Diels-Alder reactions, the semi-empirical/AM1 level of theory that will be used throughout the experiment should be introduced. The semi-empirical level of theory is based on the Hartree-Fock theory described previously. However, as described previously, the Hartree-Fock method makes many approximations and this can often lead to errors being computed. Thus, the semi-empirical level of theory, the results produced are fitted under a set of parameters such as to produce data that best agrees with the experimental data. The AM1 calculation is based on the Neglect of Differential Diatomic Overlap integral approximation which decreases the complexity of the calculations in comparison to the Hartree-Fock equations discussed previously.

Diels-Alder cycloaddition of ethene and cis-butadiene

Optimising the ethene and cis-butadiene reactants

Prior to studying the Diels-Alder cycloaddition of ethene and cis-butadiene, these reactants will first be optimised at the Semi-Empirical/AM1 level of theory. Using Gaussview, a molecule of cis-butadiene and ethene were built and optimised in an Opt+Freq job type at the level of theory stated above. The results of these calculations are provided in the next two sections.

Cis-butadiene

The cis-butadiene molecule was optimised, as stated above, to provide the results which are shown in the table below. N.B. The dihedral angle of the butadiene molecule had been changed to 0° to build a butadiene molecule in the cis conformation.

Jmol Structure	Calculation Summary	Point Group	Energy (Hartrees)
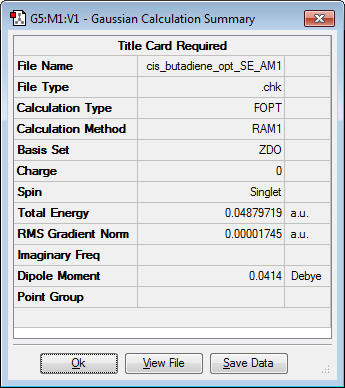		C2v	0.04879719

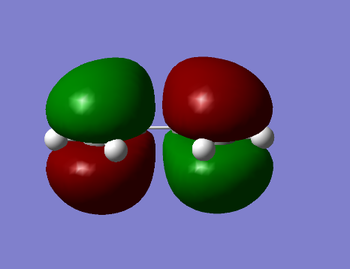
From the Opt+Freq job type carried out, the molecular orbitals of cis-butadiene can be obtained. The HOMO and LUMO of cis-butadiene are given below.

HOMO of cis-butadiene	LUMO of cis-butadiene
Antisymmetric	Symmetric

Thus, one can observe that the HOMO is antisymmetric with respect to the plane bisecting the C-C single bond whilst the LUMO is symmetric with respect to this plane.

Ethene

Similarly, a molecule of ethene was optimised at the Semi-Empirical/AM1 level of theory using an Opt+Freq job type. The results of this calculation are shown below.

Jmol Structure	Calculation Summary	Point Group	Energy (Hartrees)
		D2h	0.02619028

Once again, having done a frequency analysis, it is possible to analyse the molecular orbitals of ethene. The HOMO and LUMO are shown below.

HOMO of ethene	LUMO of ethene
Symmetric	Antisymmetric

One can observe that the HOMO of ethene is symmetric with respect to the plane containing the molecule whilst the LUMO is antisymmetric.

Optimising the transition state for the Diels-Alder cycloaddition of ethene and cis-butadiene

Having now successfully optimised the reactants, it is possible to determine the transition state for this Diels-Alder cycloaddition by carrying out further calculations. The transition state structure was obtained by optimising to a TS(Berny) (this was used earlier when finding out the transition state for the Cope Rearrangement for 1,5-hexadiene from a guess structure). Using the optimised structures of ethene and cis-butadiene, a guess transition structure was built and the interfragment distance was changed to 2.20 Å. The optimisation was carried out the Semi-Empirical/AM1 level of theory using an Opt+Freq job type. The results of this calculation is shown below.

Jmol Structure	Calculation Summary	Energy (Hartrees)
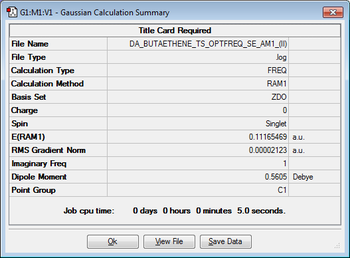		0.11165469

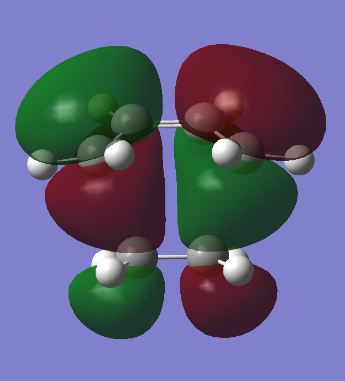
Having done a frequency analysis, the molecular orbitals can be obtained and the HOMO and LUMO of the transition state are shown below.

HOMO of transition structure	LUMO of transition structure
Antisymmetric	Symmetric

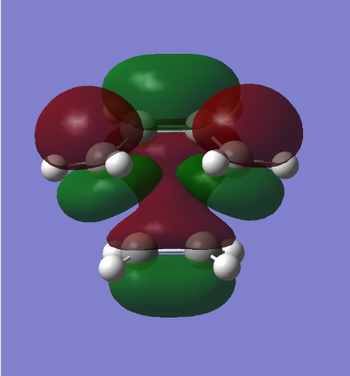The HOMO of the transition state is antisymmetric and the LUMO is symmetric with respect to the plane. It can be seen that the HOMO of cis-butadiene combines with the LUMO of ethene to form the HOMO, which is antisymmetric, of the transition state. To complete this argument, the LUMO of the transition state can bebuilt by combination of the HOMO of of ethene, which is symmetric, and the LUMO of cis-butadiene, which is antisymmetric.

(The LUMO of cis-butadiene is symmetric. Benefit of the doubt here, as you've said before that it is symmetric, but be careful Tam10 (talk) 11:27, 26 November 2015 (UTC))

From examination of the vibrational frequencies of the transition structure, one can see the presence of an imaginary frequency, which is shown below, and so this confirms that the structure obtained is indeed a transition state. This vibration, of frequency -956.40 cm^-1, shows the synchronous bond formation at bond ends of each fragment as the fragments move together. The two newly forming C-C bonds form at the same time and hence the reaction is concerted.

The imaginary frequency that leads to the Diels-Alder cycloaddition of ethene and cis-butadiene.

On the other hand, when observing the lowest positive vibrational frequency, of frequency 147.00 cm^-1, it can be seen that this vibration is not allowed in any bond forming or bond breaking process and so does not lead to a reaction. In this vibration, neither fragment moves towards or away from each other and so no bond formation occurs. It can be concluded that all positive frequencies are perpendicular to the imaginary frequency and so none of them correspond to the fragments moving together and forming bonds.

(Perpendicular is the wrong word here. The modes are independent or uncoupled to each other Tam10 (talk) 11:27, 26 November 2015 (UTC))

The first positive vibrational frequency of the transition structure.

Overall this reaction is allowed as the energies of the HOMO of the cis-butadiene and the LUMO of the ethene are close in energy to be able to interact. Thus, this interaction allows new σ bonds to form between the fragments. The HOMO of cis-butadiene and the LUMO also have the same symmetry and are in phase when the reaction occurs and so the reaction is allowed.

Analysis of the geometry of the transition structure from the Diels-Alder cycloaddition of ethene and cis-butadiene

Fig. 13 The numbering of the atoms of the transition state from the reaction of ethene and cis-butadiene

Table. C-C bond lengths for the ethene + cis-butadiene transition structure using the numbering from Fig. 13

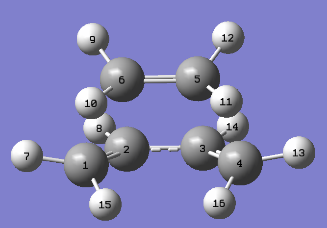
Atoms	Bond Length (Å)
C1-C2	1.38186
C2-C3	1.39748
C3-C4	1.38187
C5-C6	1.38291
C1-C6	2.11924
C4-C5	2.11915

In this reaction, a C-C single bond is forming between C1 and C6 and between C4 and C5. It can be seen that the C-C distances in this case is 2.12 Å which is shorter than the originally inputted inter fragment distance of 2.20 Å. Thus it shows that C-C bonds are beginning to form in the transition structure due to the overlap of the HOMO of the cis-butadiene and the LUMO of the ethene bringing the fragments together. This is further backed up by observing that the C1-C6 and C4-C5 bond lengths are much shorter than twice the Van der Waals radius for a carbon atom, which is around 1.70 Å , which indicates that the sigma bonds are forming. It should be noted that the sp³ and sp² C-C bond lengths are 1.54 Å and 1.33 Å respectively . On examination of other bond lengths within the cyclic transition state. It can be seen that the bond length of C2-C3 is intermediate that of a double and a single bond showing that a π bond is now forming between these two carbons. The opposite is true for the bonds C1-C2,C3-C4 and C5-C6 in which a π bond is now breaking to leave a single bond which explains why these lengths are intermediate between a single and a double bond length.

(Just because the C-C distance is shorter than the input distance, this does not suggest a transition state necessarily. Distances shorter than the Van der Waals radii would indicate a bonding interaction of some kind. It is the single imaginary frequency that truly confirms that it is a transition state Tam10 (talk) 11:27, 26 November 2015 (UTC))

The regioselectivity of the Diels-Alder cycloaddition

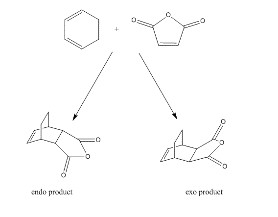
The regioselectivity of the Diels-Alder reaction will be discussed by examining the reaction between maleic anhydride and cyclohexa-1,3-diene in which an endo and exo product can be formed by different approaches of the diene to the dienophile. By computation of which transition structure is lower in energy, we can state which product, endo or exo, is preferred in terms of energetics.

Optimisation of cyclohexa-1,3-diene

A molecule of cyclohexa-1,3-diene is optimised using the Semi-Empirical/AM1 level of theory. The results of this optimisation are given below.

Jmol Structure	Calculation Summary	Point Group	Energy (Hartrees)
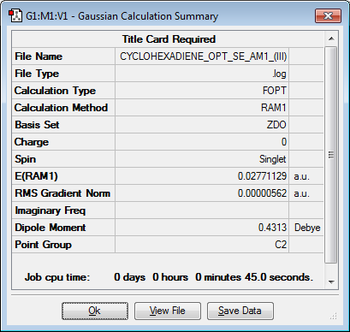		C2	0.02771129

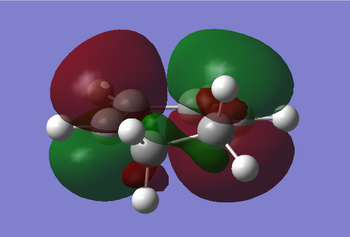
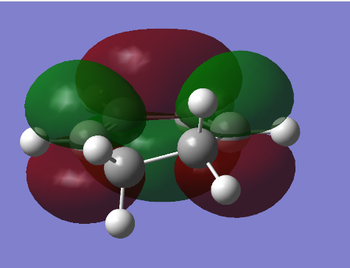
Once again, the molecular orbitals of cyclohexa-1,3-diene can be examined. In particular, the HOMO and LUMO are shown below. The HOMO is antisymmetric with respect to the plane whilst the LUMO is symmetric with respect to the plane.

HOMO of cyclohexa-1,3-diene	LUMO of cyclohexa-1,3-diene
Antisymmetric	Symmetric

Optimisation of maleic anhydride

Similarly, an optimisation of the maleic anhydride molecule was carried out using the Semi-Empirical/AM1 level of theory. The results of the calculation are shown below.

Jmol Structure	Calculation Summary	Point Group	Energy (Hartrees)
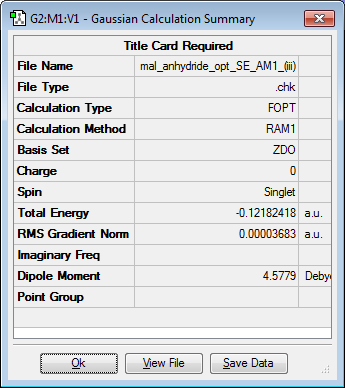		Cs	-0.12182418

(The symmetry of maleic anhydride should be C2v Tam10 (talk) 11:27, 26 November 2015 (UTC))

The molecular orbitals are once again examined and the HOMO and LUMO of maleic anhydride are shown below. The HOMO is symmetric with respect to the plane whilst the LUMO is antisymmetric with respect to the same plane.

HOMO of maleic anhydride	LUMO of maleic anhydride
Symmetric	Antisymmetric

Optimising the exo transition structure

The optimised cyclohexa-1,3-diene and maleic anhydride molecules were combined and seperated by an interfragment distance of 2.2 Å. The components were organised such that it resembled an exo product i.e. a guess structure was created. This structure was subsequently optimised using the Semi-Empirical/AM1 level of theory by optimising to a TS(Berny) to finally form an exo transition state. The results of this calculation are shown below.

Jmol Structure	Calculation Summary	Point Group	Energy (Hartrees)
		C1	-0.05041975

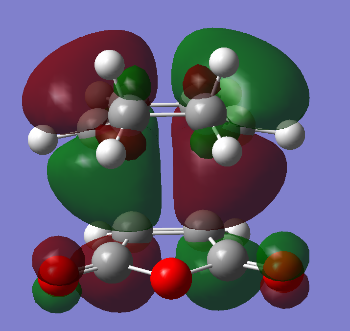
The HOMO and LUMO of the exo transition state are given below. The HOMO and LUMO are antisymmetric with respect to the plane.

HOMO of the exo transition state	LUMO of the exo transition state
Antisymmetric	Antisymmetric

Having also done a frequency analysis, it was possible to observe an imaginary frequency, of value -812.32 cm^-1, and this shows that the calculation successfully converged to the formation of the exo transition state. The vibration below also shows the movement that occurs to allow the cycloaddition to take place. Again, it shows that the new C-C bonds are formed synchronously.

Vibration leading to the Diels-Alder cycloaddition

Optimising the endo transition structure

Using the same method as for the exo transition structure, the optimised maleic anhydride and cyclohexa-1,3-diene are placed 2.2 Å apart in an endo fashion, i.e. a guess structure, such that secondary orbital interactions are possible. This resulting structure was then optimised to a TS(Berny) using the Semi-Empirical/AM1 level of theory to give the results shown below.

Jmol Structure	Calculation Summary	Point Group	Energy (Hartrees)
		C1	-0.05150477

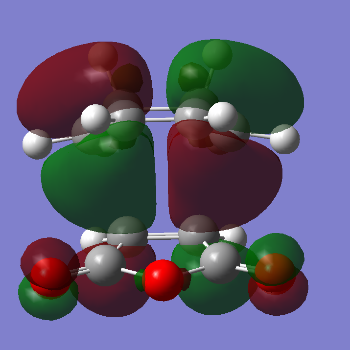
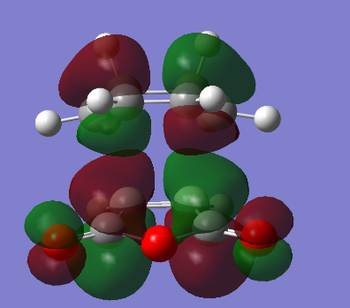
The HOMO and LUMO of the endo transition state are given below. Once again, the HOMO and LUMO are antisymmetric with respect to the plane.

HOMO of the endo transition state	LUMO of the endo transition state
Antisymmetric	Antisymmetric

An imaginary frequency, of value -806.55 cm^-1 is observed after a frequency calculation had been performed on the endo transition structure. This, therefore, confirms the formation of the transition state. The vibration shows the terminal ends of each fragment approach each other in a concerted manner and shows the two new C-C bonds being formed synchronously to lead to a cycloaddition reaction taking place.

Vibration leading to a Diels-Alder cycloaddition

Comparison of the endo and exo transition structures

Having now obtained the exo and endo transition states, one can compare the geometries and relative energies of the two transition states.

Energy of the conformers

Below the electronic energies as well as the sum of the electronic and zero-point energies and the sum of the electronic and thermal energies are given below. These values are provided for both of the reactants as well as the exo and endo transition structures at both 0 K and 298.15 K. From this we can calculate the activation energies for the process via the endo and exo transition states, these activation energies are given below.

Energies for exo, endo transition structures and reactants, cyclohexa-1,3-diene and maleic anhydride, at AM1 (Semi-Empirical)

	AM1 Semi-Empirical
	Electronic energy (Hartrees)	Sum of electronic and zero-point energies (Hartrees)	Sum of electronic and thermal energies (Hartrees)
		at 0 K	at 298.15 K
Exo TS	-0.05041975	0.134880	0.144881
Endo TS	-0.05150477	0.133493	0.143682
Cyclohexa-1,3-diene	0.02771129	0.152502	0.157726
Maleic anhydride	-0.12182418	-0.063346	-0.058192

	Electronic Energy (Hartrees)	Relative energy (kcal/mol)
Exo Transition structure	-0.05041975	0.680860
Endo Transition structure	-0.05150477	0

From inspection of the relative energies, the endo transition state is lower in energy and so the Diels-Alder cycloaddition between maleic anhydride and cyclohexa-1,3-diene takes place via an endo transition state, as it has a lower activation energy, to form an endo product. The relative energies were calculated using the electronic energies. The exo transition state is higher in energy due to steric reason. There are steric interactions between the lone pairs of the ether oxygen on the maleic anhydride and the sp³ hydrogens on the -CH₂ groups. This interaction is pronounced in the exo state as the these orbitals are eclipsing and clashing with one another which can be further increased in the transition state when the components approach each other more closely. Moreover, the nodal properties of the HOMO, of both of the exo and endo transition structures, between the -(C=O)-O-(C=O)- and the remainder of the fragment were analysed. There are more nodes present between the -(C=O)-O-(C=O)- and the remainder of the fragment in the endo transition structure than the exo transition structure.

Below, the summary of the activation energies are provided.

Summary of activation energies (in kcal mol^-1)

	AM1 Semi-Empirical	AM1 Semi-Empirical
	at 0 K	at 298.15 K
ΔE (Exo TS) (kcal/mol)	28.690339	28.455651
ΔE (Endo TS) (kcal/mol)	27.820612	27.703267

From examination of the activation energies, this data further confirms that the cycloaddition prefers to occur via an endo transition state as the activation energies are lower when passing through the endo transition structure.

Comparison of bond lengths

The C-C bond lengths were obtained for the endo and exo transition states by using the numbering system for transition structures as shown by the figures below. The tables below give the C-C bonds for the exo and endo transition structures for specific C-C bonds.

Numbering of the exo transition state	Numbering of the endo transition state

Bond lengths for exo transition state

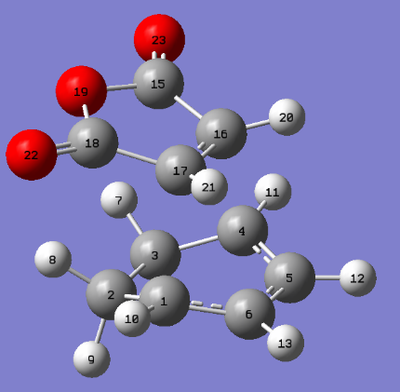
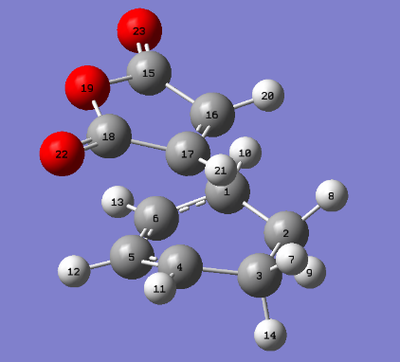
Atoms	Bond Lengths (Å)
C5-C6	1.39674
C6-C1	1.39439
C1-C2	1.48975
C2-C3	1.52210
C1-C17	2.17056
C17-C16	1.41015
C15-C16	1.48817

Bond lengths for endo transition state

Atoms	Bond Lengths (Å)
C5-C6	1.39725
C1-C6	1.39307
C1-C2	1.49054
C2-C3	1.52298
C1-C17	2.16243
C17-C16	1.40850
C16-C15	1.48924

(GaussView states a very high level of precision, but the error level is very high. As such, it's not correct to state a bond length beyond the second decimal place, really Tam10 (talk) 17:17, 26 November 2015 (UTC))

Immediately, it can be seen that the new σ bond being formed (i.e. C1-C17) is significantly shorter in the endo transition structure than the exo transition structure. This again confirms that the endo transition state is the preferred transition state to pass through during the Diels-Alder cycloaddition of maleic anhydride with cyclohexa-1,3-diene as there are much greater orbital interactions which means that the fragments are pulled closer together to maximise these favorable interactions. In both the exo and endo forms, the new σ C-C bond being formed is less than twice the VdW radius of a carbon atom, 1.70 Å, which shows that C-C bond is in the process of being formed in both processes and shows that reaction will occur via the exo and endo transition structures. Overall, there are favorable interactions between the maleic anhydride and the cyclohexa-1,3-diene in both transition states but these favorable interactions are greater in the endo form due to the addtionally stabilising secondary orbital interactions. These secondary orbital interactions also provide another reasoning as to why the exo transition state is more strained.

(Use this paragraph as an opportunity to tie everything together as to why the endo TS is lower in energy. This includes the steric hindrance (evidenced by the distance between the side groups in the exo TS being shorter than 2xVdW). Then you can mention that this prevents as much of the favourable overlap as the endo TS has access to Tam10 (talk) 11:27, 26 November 2015 (UTC))

Secondary Orbital Overlap Effects

This interaction acts to stabilize a molecule through the overlap of π orbitals of the diene and the dienophile. This effect allows the endo transition state to be lower in energy than the exo transition state. This is because there is a favorable interaction between the π orbitals of the carbon atoms on the diene and the C=O π orbitals of the maleic anhydride. This secondary orbital interaction is a non-bonding interaction but it lowers the total energy of the transition state and thus lowers the activation energy which increases the rate of the cycloaddition process for the endo transition state. Thus the endo product is kinetically favoured whilst the exo product is thermodynamically favoured. The secondary orbital interaction is not possible in the exo transition state as the C=O π orbitals are directed in the opposite direction from the π system of the diene.

Conclusions

In summary, this computational experiment studied the Cope Rearrangement of 1,5-hexadiene and the Diels-Alder reactions of cis-butadiene and ethene as well as the reaction between cyclohexa-1,3-diene and maleic anhydride on the Gaussian program.

For the Cope Rearrangement, a variety of different levels of theory, such as the B3LYP/6-31G(d) and HF/3-21G levels of theory, were used throughout the study and the results provided by each of these calculations were compared and contrasted. It was found that the B3LYP/6-31G(d) level of theory is far superior in accuracy compared to the Hartree-Fock level of theory as the Density Functional Theory takes in account fewer approximations in its calculations to give a more accurate result. The transition states, both the chair and boat structures, for the Cope Rearrangement were discussed and the formation of the transition states from the calculations had been confirmed by the presence of a single imaginary vibrational frequency. This vibration involved the reactant undergoing the Cope Rearrangement whilst all other positive vibrations were not involved in the reaction process. Moreover, the activation energies for the Cope Rearrangement using the different levels of theory were compared and it was found that the B3LYP/6-31G(d) level of theory produced much greater accuracy in the results. It was found that the Cope Rearrangement was more favorable through the chair transition state than the boat transition state.

In terms of the Diels-Alder reactions that were examined, all calculations were carried out using the SE/AM1 level of theory which proved to be sufficient. The Diels-Alder cycloaddition reaction between ethene and cis-butadiene provided simplistic results which didn't provide much information on the Diels-Alder reactions apart from confirming the concerted nature of the reaction through the synchronous bond formation of the C-C bonds between the ethene and c-butadiene. However, the regioselectivity of the Diels-Alder reaction was studied in depth by inspecting the reaction between maleic anhydride and cyclohexa-1,3-diene. This study showed that the process was faster, i.e. had a lower activation energy, when passing through the endo transition structure due to stabilising secondary orbital interactions which are not present in the exo structure. Finally, when comparing the energetic and geometric properties of the endo and exo transition structures, it can be found out that the exo transition structure is more strained due to fewer stabilising interactions and more steric clashes between the oxygen lone pairs of the maleic anhydride and sp³ hydrogens on the diene.

Having thoroughly evaluated this computational study, there are many factors that could have been implemented to produce more accurate and reliable results. Firstly, one could have tried the Frozen Coordinate Method for the formation of the transition states in the Diels-Alder reactions to allow for a broader comparison. Moreover, an extended study on the formation of the boat transition structure of the Cope Rearrangement could have been carrried out by optimising using the QST3 method to see any changes from the results of the calculation compared to the QST2 method. Further research could have been done on studying both the Cope Rearrangement and Diels-Alder reactions using aza-1,5-dienes and hetero dienes and dienophiles respectively. This can be studied to see if the preferred route for the reactions had changed. For example, it could be studied whether the Diels-Alder reaction is still preferred via the endo transition structure energetically when hetero dienes/dienophiles are used. The heteroatom used can be either oxygen, sulfur or nitrogen.