Rep:Mod:UHU6078
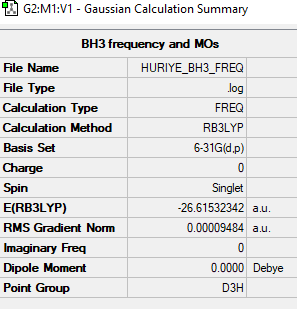
BH3 Molecule
B3LYP/6-31G(d,p)
Item Value Threshold Converged? Maximum Force 0.000190 0.000450 YES RMS Force 0.000095 0.000300 YES Maximum Displacement 0.000747 0.001800 YES RMS Displacement 0.000374 0.001200 YES
Low frequencies --- -0.2260 -0.1035 -0.0053 48.0308 49.0904 49.0909 Low frequencies --- 1163.7225 1213.6715 1213.6742
Frequency file could be found: here
optimised BH3 molecule |
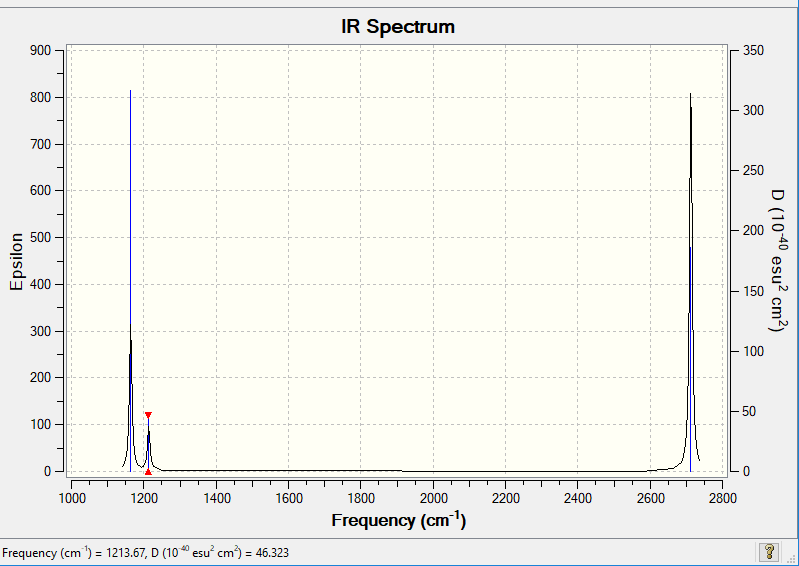
Vibrational spectrum for NH3
| wavenumber (cm-1 | Intensity (arbitrary units) | symmetry | IR active? | type |
| 1164 | 92 | A2 | Yes | Out of plane bend |
| 1214 | 14 | E | Yes | In plane bend |
| 1214 | 14 | E | Yes | In phane bend |
| 2580 | 0 | A1 | No | Symmetric Stretch |
| 2713 | 127 | E | Yes | Asymmetric Stretch |
| 2713 | 126 | E | Yes | Asymmetric Stretch |
3N-6 allows for the calculation of the number of different vibrational modes. Since the number of atoms in the molecule is 4, 6 different modes of vibration is expected. In the IR spectrum there are 3 peaks instead of 6. In order to be IR active, a vibrational mode should result in a change in dipole moment. Overall, the symmetric stretch of the B-H bonds give no change in dipole moment. As a result this mode is not observed in the IR spectrum.
It could be seen from the table that there are two sets of degenerate modes. The second and third bending modes have the same energy and so only one peak occurs in the spectrum. The same is true for the fifth and sixth stretches. For each degenerate pair only one peak appears in the spectrum which explains why the other two expected peaks are absent.
Molecular Orbital Diagram[1]
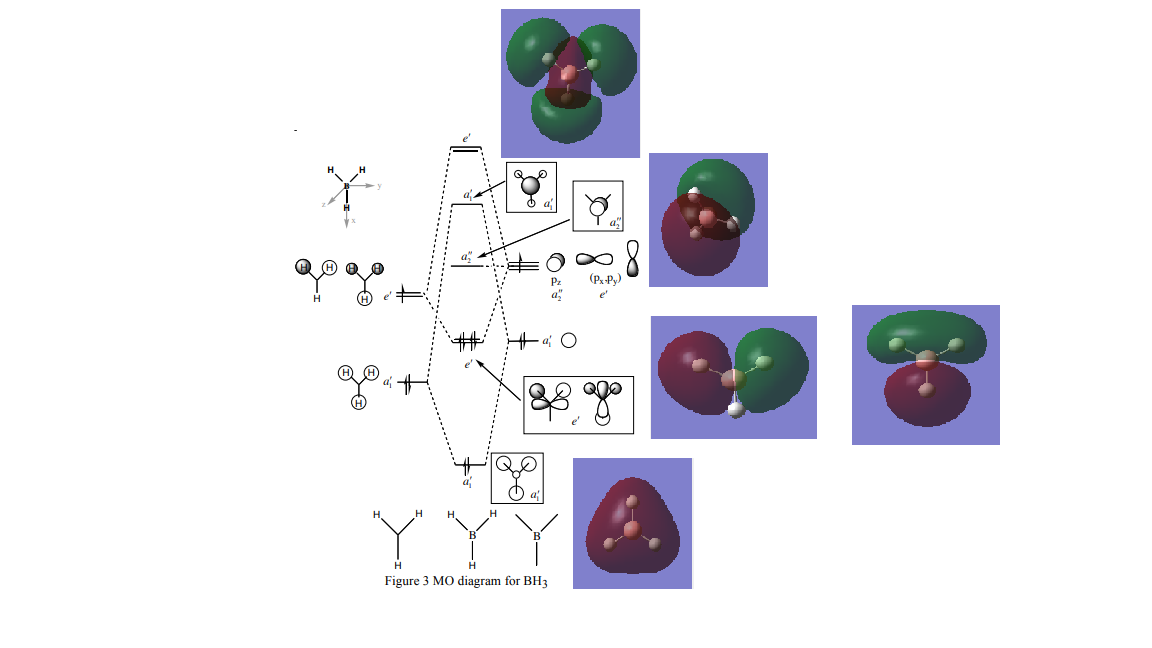
Linear combination of atomic orbitals and the real molecular orbitals are very similar. Qualitative MO theory is thus very useful and accurate in predicting the real Molecular Orbitals. As shown in the example above, most of MOs from LCAO were successful in giving a thorough idea about the real MOs. It is mostly the amount of space covered by the molecular orbitals which is hard to predict by the theory.
Ng611 (talk) 00:14, 22 May 2019 (BST) Good MO diagram! Are there any other differences you can see?
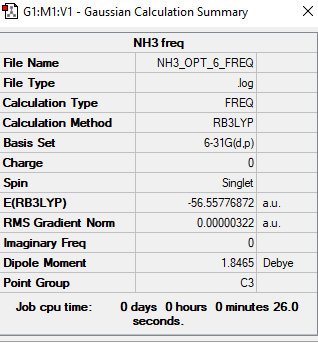
NH3 Molecule
B3LYP/6-31G(d,p)
Item Value Threshold Converged? Maximum Force 0.000006 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000016 0.001800 YES RMS Displacement 0.000011 0.001200 YES
Low frequencies --- -0.0137 -0.0027 0.0007 7.0783 8.0932 8.0937 Low frequencies --- 1089.3840 1693.9368 1693.9368
Frequency file could be found: here
optimised NH3 molecule |
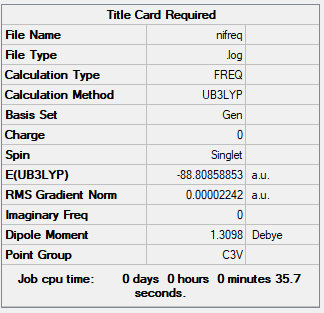
NI3 Molecule
B3LYP/6-31G(d,p)
Item Value Threshold Converged? Maximum Force 0.000063 0.000450 YES RMS Force 0.000022 0.000300 YES Maximum Displacement 0.000918 0.001800 YES RMS Displacement 0.000339 0.001200 YES
Low frequencies --- -12.5754 -12.5691 -5.9483 -0.0040 0.0191 0.0670 Low frequencies --- 100.9745 100.9752 147.3175
Frequency file could be found: here
optimised NI3 molecule |
Optimised N-I bond length: 2.1839 Å
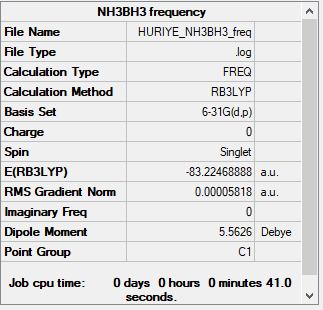
NH3BH3 Molecule
B3LYP/6-31G(d,p)
Item Value Threshold Converged?
Maximum Force 0.000138 0.000450 YES
RMS Force 0.000038 0.000300 YES
Maximum Displacement 0.000764 0.001800 YES
RMS Displacement 0.000181 0.001200 YES
Low frequencies --- -11.2646 0.0009 0.0010 0.0011 9.7382 9.9016 Low frequencies --- 262.8938 631.2165 638.0902
Frequency file could be found: here
optimised NH3BH3 molecule |
E(NH3)= -56.55777 au E(BH3)= -26.61532 au E(NH3BH3)= -83.22469 au ΔE=-83.22469-[-56.55777+-26.61532] =-0.0516 au = -138 kJ.mol<sup>-1</sup>
Ng611 (talk) 00:18, 22 May 2019 (BST) Good calculation, but you used the wrong conversion factor so your answer in kJ/mol is incorrect. Otherwise, excellent.
A C-C bond is considered to be a very strong bond. It has a dissociation energy of about 350 kJ.mol-1. A relatively weak bond, F-F requires around 150 kJ.mol-1 for the bond to break. Since the bond energy of the dative bond is even lower than an F-F bond, N-B bond could be said to be very weak.[2]
Ng611 (talk) 00:20, 22 May 2019 (BST) Good comparisons. I'd use a text reference as opposed to websites though.
Mini Project 3
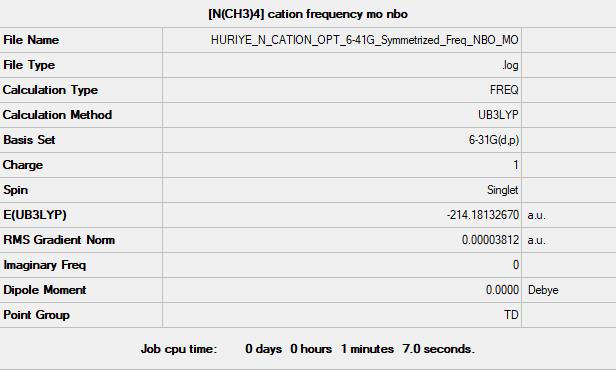
[N(CH3)4]+ Ion
B3LYP/6-31G(d,p)
Item Value Threshold Converged? Maximum Force 0.000014 0.000450 YES RMS Force 0.000008 0.000300 YES Maximum Displacement 0.000193 0.001800 YES RMS Displacement 0.000075 0.001200 YES
Low frequencies --- 0.0010 0.0011 0.0013 34.7310 34.7310 34.7310 Low frequencies --- 216.9839 316.2350 316.2350
Frequency file could be found: here
optimised [N(CH3)4]+ Ion |
Molecular Orbitals
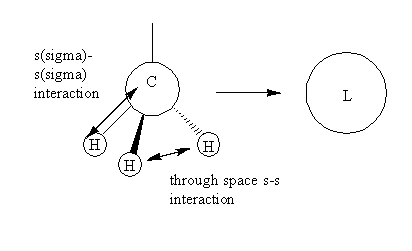
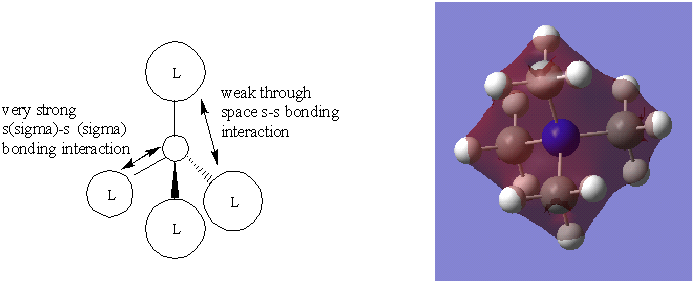
The MO theory employs 4 methyl fragments and a Nitrogen atom in order to build a MO diagram for [N(CH3)4]+ ion. Fist and second MO diagrams below use a methyl fragment that results from the in phase overlap of s(sigma)-s(sigma) orbitals and through space s-s bonding interactions of the s orbitals of the H atoms, producing a symmetrically spherical orbital, an s orbital.
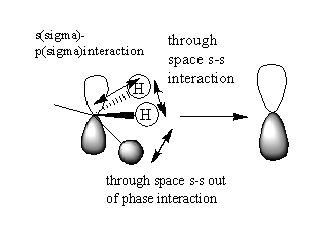
The third MO presented below uses one of the triply degenerate MO of the methyl fragment. They are triply degenerate because they are formed by combining a 2p orbital of the carbon and three s orbitals of Hydrogens, one of which is at a different phase. This type of interaction takes place for the other two 2p orbitals of carbon, each resulting in a p-like ligand orbital.
Ng611 (talk) 00:22, 22 May 2019 (BST) Excellent MO analysis!
Ligand orbitals representation
Molecular Orbitals
The MO presented above has no nodal planes, all of the interactions are in-phase. The strongly bonding MO has two different orbital interactions. Overlap between two s orbitals through a bond tend to be very strong since they are very dense. The interaction strength decreases as the distance between the orbitals increases. In this case the interaction between ligands are through space and so weaker.
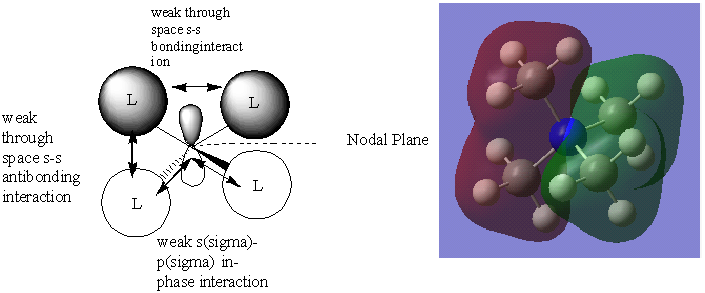
In this case the interaction takes place between the s orbital like ligands and a p orbital from the Nitrogen atom. The s and p orbitals are not completely directed to each other which makes the overlap less good. The antibonding interactions result in the the nodal plane shown above. There are two more different combinations of the s like methyl fragments with the 2 other 2p orbitals of N resulting in 3 degenerate orbitals overall.
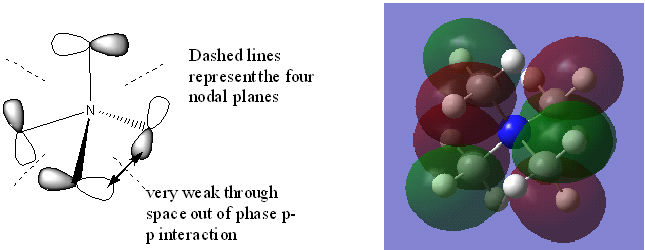
This MO is a non-bonding orbital. There is no orbital contribution from the Nitrogen atom. The antibonding interactions are through space and between p orbitals. P orbitals are more diffuse than s orbitals which makes the through space interaction between p orbitals even weaker.
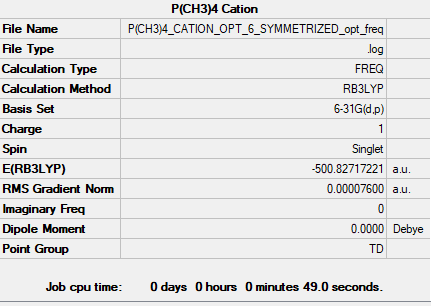
[P(CH3)]4+ Ion
B3LYP/6-31G(d,p)
Item Value Threshold Converged? Maximum Force 0.000102 0.000450 YES RMS Force 0.000076 0.000300 YES Maximum Displacement 0.001645 0.001800 YES RMS Displacement 0.001064 0.001200 YES
Low frequencies --- -0.0031 -0.0031 -0.0019 51.3724 51.3724 51.3724 Low frequencies --- 186.7390 211.5787 211.5787
Frequency file could be found: here
optimised [P(CH3)4]+ Ion |
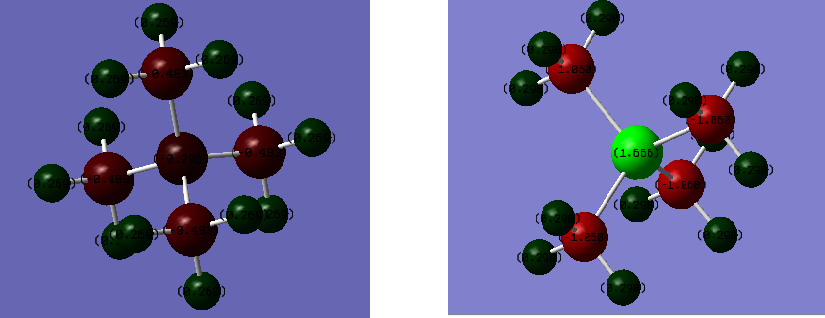
Charge Distribution Comparison
| Atom | Charge in [N(CH3)4]+ Ion | Charge in [P(CH3)4]+ |
| H | 0.269 | 0.298 |
| C | -0.483 | -1.060 |
| N | -0.295 | |
| P | 1.666 |
It could be seen that the distribution of charge in the former cation is more even when compared to [P(CH3)4]+ which has its charge distribution over a larger range. To account for this range both of the snap-shots were taken from a colour spectrum set to -2.000-2.000.
Nitrogen and Phosphorus are elements of group 5 and are found in period 2 and 3 respectively. This means that the orbital overlap between the Nitrogen and the methyl fragments will be stronger. This is because while Nitrogen uses 2s and 2p orbitals for interaction, Phosphorus uses its 3s and 3p orbitals. 3s and 3p orbitals are more diffuse and have a greater energy difference to the methyl fragments(formed by the interaction between 1s,2s and 2p orbitals) and so their interaction with the methyl fragments is less good. This decreases the symmetry of the latter cation resulting in an uneven distribution of the charges over a larger range.
Ng611 (talk) 00:26, 22 May 2019 (BST) Not sure what you mean by symmetry here. The even charge distribution over the methyl groups suggests that they're all symmetrically related. Otherwise, good answer.
Additionally, since Nitrogen is very electronegative and small in size, the atom and the methyl groups would be closer together to increase the orbital overlap giving rise to a more symmetric molecule. Phosphorus is larger, have longer bonds to methyl groups and so less effective orbital interaction results in a less symmetric molecule and so an uneven distribution of charges.
The table above also shows that while Nitrogen is negatively charged, Phosphorus is positively charged. Both Nitrogen and Phosphorus are intrinsically electron deficient because of sharing their lone pairs with the carbon. In the case of a P-C bond, the more electronegative carbon atom received greater electron density. In the case of a N-C bond, while the less electronegative carbon receives a greater share of the electrons, Nitrogen receives some negative charge. This could be explained by the high electronegativity of Nitrogen such that with the aid of being symmetric and having shorter bonds the Nitrogen atom could relieve its electron deficiency.
Both of the ions have C-H bonds. Since Nitrogen and Phosphorus are two bonds away from the Hydrogen atoms, the effect of electronegativity decreases resulting in similar charge distribution for H atoms in both of the ions.
[NR4]+ species are represented with a formal positive charge on the Nitrogen atom. Formal charge is allocated such that the definition ignores electronegativity and assumes that the electrons are shared equally in a single bond. Since a Nitrogen atom could fulfil its octet by making 3 bonds, the fourth bond is such that the lone pair on Nitrogen is used to be shared equally with the Carbon of the R group, thus Nitrogen being left electron deficient. In this case the representation of a positive formal charge on Nitrogen contradicts with the charge distribution data obtained. The positive charge should actually be located on the R groups.