Rep:Mod:Transition States cyk13
Note: Due to nature of templates used the page may not align well at certain zoom/resolution/size of browser/screen, please adjust accordingly.
Cope Rearrangement
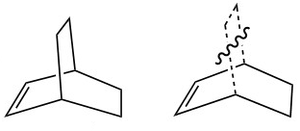
The Cope Rearrangement of 1,5-hexadiene is studied in the following section by finding the minimum of the reactants/products and calculating the energies and orientations of the transition states. The reaction is a [3,3]-sigmatropic reaction with mechanism and transition states shown in Figure 1.[1][2]
Optimization
Hexadiene
| Allyl Fragment opt | |||
|---|---|---|---|
| Job Type | Minimum Optimisation | ||
| Method | HF 3-21G | ||
| Total Energy | (-115.82304010 a.u.) | ||
| RMS Gradient Norm | 0.00003048 a.u. | ||
| Notes | pointgroup:C2v | ||
| hexadiene 5 6-31G* reopt | |||
|---|---|---|---|
| Job Type | Minimum Optimisation | ||
| Method | DFT B3LYP/6-31G* | ||
| Total Energy | (-234.61171166 a.u.) | ||
| RMS Gradient Norm | 0.00001217 a.u. | ||
| Thermo-chemistry* | (-234.469215) | ||
| (-234.461866) | |||
| (-234.460922) | |||
| (-234.500800) | |||
| Notes | reoptimisation of hexadiene 5 | ||
Hexadiene (Both the product and the reactant) is optimised to minimum by method and basis shown on the left. The process is done several times with different starting conformations as several different minima exist for the molecule. The orientation that the optimised molecule corresponds to as shown in instructions is noted.
Note: representations by JSmol is highly inaccurate in representing its respective log file, including number of bonds and bond lengths. Graphics provided by JSmol only serves as a approximate idea of how the molecule approximately looks. The original log file uploaded on wiki or the data in the tables can give a more accurate representation of the optimised molecule(s). Screen caps will be used instead in cases of large deviation in even the shape of the molecule.

In the five conformations found, from the most stable (most negative total energy) to least stable: gauche 3>anti 1>anti 2>gauche 2>gauche 6. In most cases it abides by the general rule that anti conformations are slightly more stable than gauche conformations, with the exception of gauche 3 (Hexadiene opt) This is due to 1,5-hexadiene, having 6 C atoms, can form far more conformations that the dihaloethane or butane that is often used to demonstrate the energy differences of difference conformation as seen in Figure 2.
It can be easily observed that the conformations that have lower total energy (a.k.a. more stable) have chains that are "straighter" and minimal interactions between atoms except their neighbours. The gauche conformations are often ring-like with the carbons on the ends of the molecule being close to each other. The electronic repulsion contributes to a higher overall energy of the computed conformation.
Although the gauche conformations may look similar at a glance, it can bee seen with careful inspection that gauche 6, when looked at along the bonds of C2 and C3, C1 and C4 overlaps completely, making it the least stable of all. Gauche 2, when looked at along the bonds of C3 and C4, C1 and C6 mostly overlaps. However, being much further apart it doesn't destabilise the conformation as much as gauche 6. In gauche 3 none of the carbon atoms overlap no matter along which bond it is observed from, making it the most stable of all.
Finally anti 2 (optimisation 5) is taken and re-optimised at a higher level of theory as shown on the left.
Nf710 (talk) 14:37, 5 November 2015 (UTC) You havent shown a huge understanding of the methods or how the optimisation works. You also have done a frequency calculation to show you have got a minimum, nice use of JSmol though. The lowest energy conf is the gauche 3 due to the secondry orbital interactions that occur between the two pi bonds.
Allyl fragment
As shown in figure 1 the transition state of the Cope Rearrangement consists of two identical allyl fragments of the formula C3H5. Thus this fragment is essential to the computation of the transition state. The fragment was built accordingly, optimised and used in the following section to find the transition state.
Transition State Optimization
TS (Berny) Optimization: Chair
Two allyl fragments were taken and placed in a conformation resembling the chair conformation of cyclohexane as in Figure 3[4]. The terminal (interacting) carbon atoms were placed 2.2 Å apart from each other, a distance where the two fragments can interact but not bond. A transition state optimisation was done as shown on Chair Transition State. Nf710 (talk) 14:39, 5 November 2015 (UTC)you have produced a TS the gradient has converged if you look in the log file and the imaginary frequency is The structure has a gradient of 0.00001063 a.u., suggesting that it is at either minimum or maximum. The presence of imaginary vibration, showing a vibration that causes the terminal C atoms to approach each other, suggests that the optimised structure is a transition state. | |||||||||||||||||||||||||
Optimization by Freeze Coordinate: Chair
Another method was also employed to find the transition state at the chair conformation. The distance between the terminal C atoms are frozen to 2.2 Å using Redundant Coordinates Editor and then optimised to minimum. The resultant molecule was then taken and the distances between the atoms unfrozen and set to derivative. That was optimised again, this time optimised to transition state (Berny) Comparing the results with the chair transition state done in a more direct way in the previous section it can be seen that the numbers all agree with each other very well. Apart from the fact that the two looks the same, the total energy, the imaginary vibration, distance of the C atoms and all the thermochemistry energies agree with each other to very close proximity. It can be concluded that the two methods yielded the same transition state of the chair conformation. | |||||||||||||||||||||||||
TS (QST2) Optimization: Boat
A third method was attempted in computing the transition state of the reaction at boat conformation. The reactant and product of the reaction is both built as separate molecules in the same molecule group. TS (QST2) is used instead of TS (Berny) and transition state was computed according to the reactant and product provided. To avoid confusion (of the computer) all atoms were labeled to correspond to the same numbered atom of the reactant/product.  Nf710 (talk) 14:43, 5 November 2015 (UTC) your calculations are all correct here but your boat structure looks abit off. The first computation was unsuccessful as the reactant and product were not aligned in a way close to being a ring and the computation did not take into account certain possible bond rotations to give the correct transition states. The transition state resulted had the atoms interacting across each other giving a X shaped bonds-to-be-made as seen in figure 4, which is obviously not the case in the real situation. The reactant and product previously built was taken and modified to a conformation where the terminal C atoms are closer together (central C-C-C-C dihedral angle set to 0o and inside C-C-C angel to 100o). TS (QST2) calculation was carried out once more to give the resulting transition state. Comparing the figures between the chair and boat transition states it can be seen that boat transition state, with a less negative total energy, is less stable than that of chair. The same is supported by thermochemistry figures, in which the boat conformation all has less negative values. | |||||||||||||||||||||||||
Intrinsic Reaction Coordinate
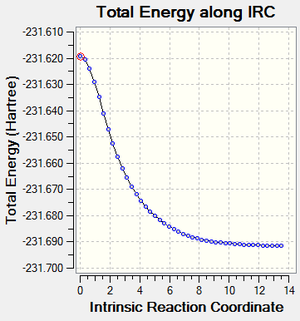 Intrinsic Reaction Coordinate (IRC) can be used to simulate the reaction path of the transition molecule to its product(s) and/or back to its reactant(s). The chair transition state computed previously was taken and put through the IRC (HT 3-21G, always calculate force constants, N=50). This results in a series of geometries in which the one of the terminal C atoms of each of the two allyl fragments approach each other (just as shown in the imaginary vibration), forming a C-C bond. The newly formed 1,5-hexadiene then continued to be optimised to the minimum where the product/reactant is at, which resembled gauche 2 geometry previously computed. The final geometry has a gradient of 0.00015225 a.u., which can be satisfactorily accepted as the conformation of the product/reactant, though not as at the minimum as optimised molecules. The IRC path in figure 5 resembles that of a half of a typical reaction pathway, showing that the energy of the molecule drops from its maximum (the transition state) to the product/reactant, the minimum. Thus, the final conformation was taken and optimised (HF 3-21G) to give a molecule with total energy of 231.69166702 a.u. and gradient of 0.00000475 a.u., in which the former is exactly the same as the optimised gauche 2 conformation of 1,5-hexadiene, just as predicted previously. |
Activation Energies
Re-optimization
To find the activation energies that 1,5-hexadiene has to go through either from chair or boat conformation, transition states of both the chair and boat conformation were re-optimised at a higher level of theory of DFT B3LYP/6-31G*. The figures of energies (thermochemistry) were then taken and calculated to give the activation energies as shown in the part below. |
| ||||||||||||||||||||||||||||||||||||||||||||||||||
Calculations
| HF 3-21G | Electronic energy | Sum of electronic and zero-point energies (0K) | Sum of electronic and thermal energies (298.15K) |
|---|---|---|---|
| Chair TS | -231.6193225 | -231.466701 | -231.461341 |
| Boat TS | -231.60280238 | -231.450929 | -231.445300 |
| Hexadiene (anti 2) | -231.6925353 | -231.539540 | -231.532566 |
| Activation Energies (Chair) | 0.072839 a.u. 45.707 kcal/mol |
0.071225 a.u. 44.694 kcal/mol | |
| Activation Energies (Boat) | 0.088611 a.u. 55.604 kcal/mol |
0.087266 a.u. 54.760 kcal/mol |
| DFT B3LYP/6-31G* | Electronic energy | Sum of electronic and zero-point energies (0K) | Sum of electronic and thermal energies (298.15K) |
|---|---|---|---|
| Chair TS | -234.556931 | -234.414908 | -234.40898 |
| Boat TS | -234.5430788 | -234.402356 | -234.396012 |
| Hexadiene (anti 2) | -234.6117117 | -234.469215 | -234.461866 |
| Activation Energies (Chair) | 0.054307 a.u. 34.078 kcal/mol |
0.052886 a.u. 33.186 kcal/mol | |
| Activation Energies (Boat) | 0.066859 a.u. 41.955 kcal/mol |
0.065854 a.u. 41.324 kcal/mol |
All energies in hartree unless otherwise stated. 1 hartree = 627.509 kcal/mol.
With DFT B3LYP/6-31G* being a higher level of theory it is not surprising that the activation energies calculated from that theory fits better with the actual experimental results of 33.5 ± 0.5 kcal/mol (Chair)[5] and 44.7 ± 2.0 kcal/mol (Boat)[6] at 0K.
Nf710 (talk) 14:51, 5 November 2015 (UTC)You have done the required work and computed the correct energeries, but your understanding of the theorey and going beyond the script was limited. Nice use of JSmol however.
Diels Alder Cycloaddition


Based on the transition state and minimum computations done previously on Cope Rearrangement, the [4s + 2s] Diels Alder Cycloaddtion was investigated in a similar way. Two Diels Alder reactions were computed: butadiene and ethene; cyclohexa-1,5-diene and maleic anhydride. The reaction mechanisms are as shown in figure 6[7] and 7 respectively.
Optimization: Butadiene and Ethene
To compare the energies butadiene, ethene and cyclohexene were built and optimised to minimum.
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||
Transition State Optimization: Butadiene and Ethene
The transition state was found using two different methods: direct TS (Berny) optimisation and QST2 method respectively.
TS (Berny) Optimization
 A bridged cyclohexene was built and cleaned, after which the bridge was deleted to leave a book-like conformation of cyclohexene as shown in figure 8. The molecule was only cleaned but not optimised because optimisation caused the C-C bond of the bridge to elongate and break to give 2,5-dimethylcyclohexene. Bonds between C2 C3 and C4 C5 were deleted and one and a half bonds for the rest of the C-C bonds, resembling the transition state shown in figure 6. The now two separate molecules were translated apart to 2.2 Å and TS (Berny) optimisation was carried out. The result has an imaginary vibration and proceed to cyclohexene on one way and butadiene and ethene on the other by running IRC on both directions as shown in figure 9, confirming it being the transition state. | |||||||||||||||||||||||||
TS (QST2) Optimization
 To reconfirm the transition state QST2 method was also adopted to find the transition state. It took several attempts to make sure the computer can relate the reactants to the product, the successful conformation is shown in figure 10. The resultant transition state resembles that from TS (Berny) method both in appearance and all data (all energies, vibration, length of C-C bonds to be made). IRC was also performed on this molecule to give similar results as that of TS (Berny). It is noted that the length of C-C bonds to be made are just above 2.2 Å (2.0 Å-2.14 Å for Cope Rearrangement above and 2.16 Å-2.17 Å for Diels Alder below), all of which are much longer then the typical C-C single bond lengths of approximately 1.48 Å (sp2) and 1.53 Å (sp3) (numbers concluded from various optimisation results). However it is much less then 2*Van der Waals radius of carbon atom of 1.69 Å [8] which is 3.38 Å. These suggest that the C-C bonds-to-be-made at the transition state are, though still too far apart to form C-C bonds, within the proximity to interact. The imaginary vibration corresponding to the reaction path to/from the transition state is shown in figure 11 a; the lowest positive frequency is shown in figure 11 b. Figure 11 a shows the stretches in which the terminal atoms approach each other to form/break the C-C bond. According to IRC the formation of the two C-C bonds are synchronous. Note: the gif images happen not to move on this page and reason is not known. Please click on the image to view the file (which moves). | |||||||||||||||||||||||||
 |
 |
Activation Energy
| HF 3-21G | Electronic energy | Sum of electronic and zero-point energies (0K) | Sum of electronic and thermal energies (298.15K) |
|---|---|---|---|
| Transition State | -231.6032086 | -231.4513380 | -231.4456500 |
| Butadiene | -154.0551403 | -153.9631820 | -153.9587580 |
| Ethene | -77.60098814 | -77.54590600 | -77.54294900 |
| Total energy of Reactants | -231.6561284 | -231.509088 | -231.501707 |
| Activation Energies | 0.05775 a.u. 36.239 kcal/mol |
0.056057 a.u. 35.176 kcal/mol |
All energies in hartree unless otherwise stated. 1 hartree = 627.509 kcal/mol.
Molecular Orbitals
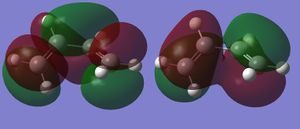 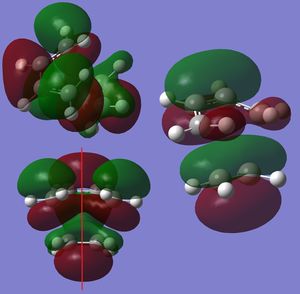 The MOs of the both optimised transition states were inspected. In Figure 12 a, both the HOMO and LUMO are anti-symmetric, but the LUMO is close to being symmetric; in Figure 12 b both the HOMO and LUMO are symmetric with respect the plane represented by the red line. (The calculations were supposed to be run with AM1. However, it's interesting to see that the lowest energy conformation for HF is twisted. You'd find that it's more symmetric for AM1. Analysis would be easier for AM1, but still works for HF. Would you expect the activation energy of AM1 to be different to HF knowing this? Tam10 (talk) 15:43, 28 October 2015 (UTC)) The HOMO and LUMO interaction of butadiene and ethene resembles that of Diels Alder Reaction with inverse electron demand, as shown in figure 13[9]. The LUMO of butadiene interacts with the HOMO of alkene. The reaction is allowed as the interacting orbitals have the same symmetries. The interactions sketched on figure 13 corresponds exactly to the computed MO of the HOMO and LUMO of the transition state, suggesting a good match between theory and computations. However, it is noted that by theory[10], the ethene LUMO and butadiene HOMO should be closer in energy then the ethene HOMO and butadiene LUMO.
1 eV equals to 23 kcal/mol, 0.037 Hartrees, or 96.5 kJ/mol Butadiene LUMO and ethene HOMO (inverse electron demand) has an energy difference of 11.5 eV; butadiene HOMO and ethene LUMO (normal electron demand) has an energy difference of 10.6 eV. As the energy of the interacting orbitals of normal electron demand are closer, in theory, the reaction should proceed by normal electron demand. 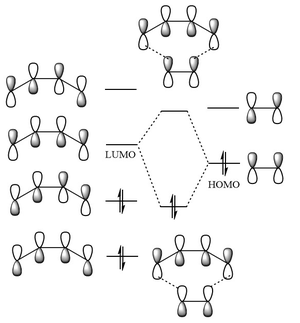 |
Optimization: Cyclohexa-1,3-diene and Maleic Anhydride
Again, in order to compare the energies all the reactants (hexa-1,3-diene and maleic anhydride) and products (exothermic and endothermic diels alder adduct) were built and optimised to minimum.
(Be careful: in the context of DA reactions, exo and endo are not the same as exothermic and endothermic! Tam10 (talk) 15:43, 28 October 2015 (UTC))
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(It doesn't seem like you're displaying the correct models in these Jmols - they look like the first step of the optimisation Tam10 (talk) 15:43, 28 October 2015 (UTC))
The exothermic product has the maleic anhydride part "pointing towards" the bridge of the six membered ring while endothermic product "points away" from the bridge. Therefore the exothermic product probably has more steric strain as the C-O-C group is closer to the -C-C- bridge then the endothermic product.
The combined energies of the diene and dienophile is -605.64674433 a.u., which is less stable then both the exothermic and endothermic products.
It is noted that, contrary to the theory, the endothermic product is more stable then the exothermic product, in terms of all energies (total and the four thermochemistry energies). The calculation is carried out again at different levels of theory, including HF 3-21G (as shown above), DFT B3LYP/6-31G* and Semi Empirical AM1. The inconsistency between theory and computation persists no matter the theory used in computation. The reason behind is not yet understood.
| HF 3-21G | DFT B3LYP/6-31G* | Semi Empirical AM1 | |
|---|---|---|---|
| Exothermic TS | -605.71873541 | -612.75577843 | -0.15990923 |
| Endothermic TS | -605.72132070 | -612.75830960 | -0.16017071 |
| Energy Difference (Exo-Endo) | 0.00258529 | 0.00253117 | 0.00026148 |
Unit in hartree. All energies are "total energy", though not shown above, thermochemistry energies show the same result of endothermic product being more stable.
From this point on most calculations are done basing on Semi Empirical AM1 theory, a more approximate theory, as the others would take far too long and too much computing power. Please note that all the subsequent calculations used the Semi Empirical AM1 optimised products instead of HF 3-21G as shown above for consistency both in comparing energies in the section above and in computation.
Transition State Optimisation: Cyclohexa-1,3-diene and Maleic Anhydride
To ensure more accurate guess structures were built when optimising for the transition state, all guesses were built upon the AM1 optimised respective products with alterations on bond order and distance between molecules (2.2 Å apart for terminal C atoms).
(You should mention sterics and their role in distorting the TS and products Tam10 (talk) 15:43, 28 October 2015 (UTC))
TS (Berny) Optimisation
The transition state of both exothermic and endothermic products were both computed in the same way and results are as shown on the right. Both TS has an imaginary vibration of the partly formed C-C σ-bonds stretch. The partly formed C-C bonds of endothermic TS are shorter than that of exothermic, possibly due to secondary orbital interactions between the reactants that happens at endothermic TS. | |||||||||||||||||||||||||
Also, note that all the energies of the endothermic TS are less positive/more negative than that of exothermic TS. Exothermic TS has a relative energy of 0.681 kcal/mol compared to endothermic TS. As the endothermic TS is relatively more stable than exothermic TS. The activation energy required for going through endothermic TS is lower as shown in the calculations below, making endothermic product the kinetic product. | |||||||||||||||||||||||||
Activation Energy
| Semi-empirical AM1 | Electronic energy | Sum of electronic and zero-point energies (0K) | Sum of electronic and thermal energies (298.15K) |
|---|---|---|---|
| Exothermic TS | -0.05041985 | 0.134881 | 0.144882 |
| Endothermic TS | -0.05150467 | 0.133493 | 0.143682 |
| Diene | 0.0277113 | 0.152502 | 0.157726 |
| Dienophile | -0.12182418 | -0.063347 | -0.058193 |
| Total energy of Reactants | -0.09411288 | 0.089155 | 0.099533 |
| Activation Energies (Exo) | 0.045726 a.u. 28.693 kcal/mol |
0.045349 a.u. 28.457 kcal/mol | |
| Activation Energies (Endo) | 0.044338 a.u. 27.822 kcal/mol |
0.044149 a.u. 27.704 kcal/mol |
| HF 3-21G | Electronic energy | Sum of electronic and zero-point energies (0K) | Sum of electronic and thermal energies (298.15K) |
|---|---|---|---|
| Exothermic TS | -605.6035912 | -605.40814 | -605.398679 |
| Endothermic TS | -605.6103682 | -605.414903 | -605.405477 |
| Diene | -230.5432311 | -230.411187 | -230.406354 |
| Dienophile | -375.1035132 | -375.042897 | -375.038063 |
| Total energy of Reactants | -605.6467443 | -605.454084 | -605.444417 |
| Activation Energies (Exo) | 0.045944 a.u. 28.830 kcal/mol |
0.045738 a.u. 28.701 kcal/mol | |
| Activation Energies (Endo) | 0.039181 a.u. 24.586 kcal/mol |
0.038940 a.u. 24.435 kcal/mol |
All energies in hartree unless otherwise stated. 1 hartree = 627.509 kcal/mol.
HF 3-21G is done on top of semi-empirical AM1 to allow comparison with the figures of reaction between butadiene and ethene . It is noted that the activation energy of this reaction is far lower then that of butadiene and ethene (35.2 kcal/mol at 298.15 K), which means this reaction proceeds more easily with less energy required. This is likely to be due to the fact that butadiene and ethene both do not have any EDG or EWG and thus their LUMO and HOMO energies lie far apart (in both normal and inverse electron demand) leading to slow reactions. In fact the reaction between butadiene and ethene has requires up to 165 °C, 900 atm and 17 hours to proceed, only to give a low yield.[11]
(Is this in the right place? Tam10 (talk) 15:43, 28 October 2015 (UTC))
Molecular Orbitals
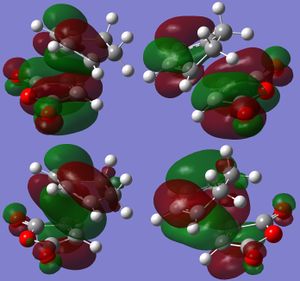 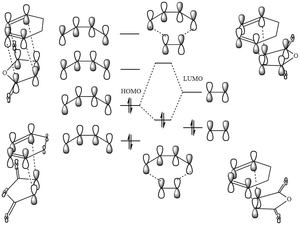 Again the MOs of the HOMO and LUMO of both the exothermic and endothermic TS were examined and plotted, in figure 14 and 15. As opposed to the reaction between butadiene and ethene previously computed the MOs show that this reaction has a normal electron demand.[12] On figure 15 the interacting orbitals of figure 14 were sketched accordingly, endothermic interaction on the right and exothermic interaction on the left, HOMO at the bottom and LUMO on top (same as figure 14) The sketched interactions matches well with the theoretical ones sketched at the top and bottom. One explanation of why the endothermic TS is more stable than the exothermic one is the secondary orbital overlap, just as shown in figure 14. The distance between the carbon atoms with secondary orbital overlap has a distance of 2.892 Å, less then 2*Van der Waals radius of carbon atom of 1.69 Å which is 3.38 Å, meaning that the orbitals of the C atoms are likely to be interacting or affecting each other. However such interaction is not clearly observed in the HOMO interaction of endothermic TS computed, as there are none or little orbitals seen on C-O-C part of maleic anhydride. |
References
- ↑ Cope; Hardy, J. Am. Chem. Soc., 1940, 62, 441
- ↑ Weist; Black; Houk, J. Am. Chem. Soc., 1994, 116, 10336-10337
- ↑ Clayden, Greeves, Warren, Organic Chemistry 2nd Ed., 2012, pp 360-366. (Picture from http://www.molvis.indiana.edu/C643_S00/lecture1/)
- ↑ Weist; Black; Houk, J. Am. Chem. Soc., 1994, 116, 10336-10337
- ↑ Gajewski; Conrad, J. Am. Chem. SOC. 1979, 101, 6693
- ↑ Weist; Black; Houk, J. Am. Chem. Soc., 1994, 116, 10336-10337
- ↑ Gajewski; Peterson; Kagel, J. Am. Chem. Soc., 1987, 109, 5545-5546
- ↑ Bondi, "Van der Waals Volumes and Radii". J. Phys. Chem., 1964, 68, 441–51
- ↑ Clayden, Greeves, Warren, Organic Chemistry 2nd Ed., 2012, pp 886-887
- ↑ Fleming, Molecular Orbitals and Organic Chemical Reactions, 2010, pp 297-300
- ↑ Fleming, Molecular Orbitals and Organic Chemical Reactions, 2010, pp 297-300
- ↑ Clayden, Greeves, Warren, Organic Chemistry 2nd Ed., 2012, pp 360-366