Rep:Mod:TomTaylorMod3a
The Transition State
The Cope Rearrangement
An example of the Cope Rearrangement is shown below:
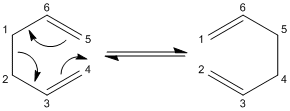
This reaction goes through either a chair cyclohexane like transition state or a boat cyclohexane like transition state. It will be investigated which of these two possible transition states the reaction goes though. But first, the reactant/product of this reaction, 1,5 hexadiene will be studied in order to find it minimum energy confirmation.
Confirmations of 1,5 Hexadiene
The different confirmations of 1,5 Hexadiene were investigated in order to find its lowest energy confirmations. In general, it can be thought that 1,5 Hexadiene can have one of two types of confirmations when looking down the carbon 3 and carbon 4 bond; Gauche or Anti. This is shown below:
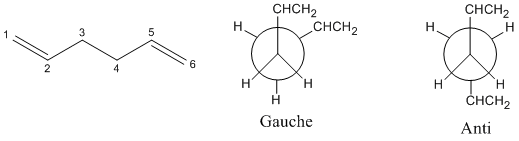
With in these two types of confirmations, a number of different confirmations are possible depending on the ordination of the -CHCH2 groups. A number of different Gauche and Anti confirmations were made and optimised to find their lowest energy confirmation and the energy of this confirmation. The find the molecules lowest energy confirmation, the molecules were optimised using the Hartree-Fock calculation method and the 3-21G basic state. The type of calculation method used determines the approximations used when solving for the energy using the Schrödinger equation and type of basic sets determines the complexity of the orbitals to used to approximate the real orbitals when solving the Schrödinger equation. The results and structures are shown below:
The names under the confirmation heading relate to the structure seen in Appendix 1 on the Module 3 wiki site.
File:Gauche1 mol.molFile:Gauche3 mol.molFile:Gauche4 mol.molFile:Anti1 mol.molFile:Anti2 mol.molFile:Anti4 mol.mol
It can be seen that the lowest energy confirmation of 1,5 Hexadiene is a Gauche confirmation (Gauche 3). This is an unexpected result as Gauche confirmations are normally higher in energy compared to Anti confirmations due to the steric interactions between the two larger groups, which are next to each other in a Gauche confirmation and opposite each other in the Anti confirmation. However, this result can be explained by looking at the Highest Occupied Molecular Orbitals (HOMO) on the Gauche 3 confirmation, which is shown below, along with the HOMO for Anti 1 confirmation for comparison:


It can clearly be seen that in the HOMO of the Gauche 3 confirmation that there is overlap and interaction between the pi-orbitals of the two alkene units. This lowers the energy of this confirmation and makes it more stable. This decrease in energy is greater than the increase in energy due to steric slashes of the confirmation (as explained above, steric slashes occur in Gauche confirmations) and makes the Gauche 3 confirmation the most stable. In comparison, it can be seen that there is not pi-orbital overlap between the two alkene units in Anti 1 confirmation and it is assumed that this is case for all Anti confirmations due to the ordination of the alkene units, which in Anti confirmations are far away from each other by virtue of being in a Anti confirmation (hence few steric slashes compared to the Gauche confirmations).
It is predicted that the Anti 2 confirmation of 1,5 hexadiene is the start confirmations (reactant) when the molecule under goes a Cope rearrangement. Therefore, a further optimisation was performed on this confirmation, using the more complex B3LYP calculation method and the 6-31G d basic set, again more complex than the 3-21G basic set. Therefore this calculation should give results closer to what is seen experimentally. Below is given some structural parameters after the optimisation using the B3LYP method and 6-31G d basic set, as well as the same parameters after the optimisation using the Hartree-Fock method and 3-21G basic set and experimental findings:
| Structural Parameter | Hartree-Fock, 3-21G | B3LYP, 6-31G d | Experimental1 |
|---|---|---|---|
| C=C Bond length | 1.32Â | 1.33Â | 1.34Â |
| C-C Bond length | 1.50Â | 1.54Â | 1.54Â |
| -C-H Bond length | 1.09Â | 1.10Â | 1.10Â |
| =C-H Bond length | 1.08Â | 1.09Â | 1.09Â |
| H-C-C Angle | 109O | 110O | 110O |
| H-C=C Angle | 122O | 122O | 1200 |
It can be seen that both calculation method/basic sets combinations give structural data that is very similar to that seen experimentally, with the more complex B3LYP/6-31G d calculation/basic set combination giving a slightly better approximation to what is seen experimentally, due to being a more complex calculation method/basic set than the Hartree-Fock/3-21G calculation method/basic set combination.
Calculations can also be performed to get other data that can be compared to what is seen experimentally. This includes the sum of electronic and zero point energies (Electronic energies and vibrational at 0K), sum of electronic and thermal energies (Electronic energies and vibrational at 298K), sum of electronic and thermal enthalpies (sum of electronic and thermal energies with enthalpy correction) and sum of electronic and free energy energies (sum of electronic and thermal energies with entropy correction). These values can be used to give predictions of energy changes for a reaction and can be compared with experiments. These 4 values are shown below, along with total energy, as calculated by the different calculation method and basic sets:
| Energy Term | Hartree-Fock, 3-21G | B3LYP, 6-31G d (298K) | B3LYP, 6-31G d (0.001K) |
|---|---|---|---|
| Sum of Electronic and Zero Point Energies | -231.5395 | -234.4792 | -234.4663 |
| Sum of Electronic and Thermal Energies | -231.5325 | -234.4619 | -234.4663 |
| Sum of Electronic and Thermal Enthalpies | -231.5316 | -234.4609 | -234.4663 |
| Sum of Electronic and Thermal Free Energies | -231.5709 | -234.5001 | -234.4663 |
| Total Energy | -231.6925 | -234.6117 | -234.6095 |
Note, it can be seen from above that for B3LYP, 6-31G d (0.001K) all the energy values are the same (-234.4663 Hartrees) except for the total energy. This is expected as temperature is very close to zero and so the values for the Sum of Electronic and Thermal Energies, the Sum of Electronic and Thermal Enthalpies and the Sum of Electronic and Thermal Free Energies will equal the Sum of Electronic and Zero Point Energies value as the former 3 expressions are exactly the same as Sum of Electronic and Zero Point Energies except they contain different additional terms for thermal energy effects and these will tend to zero as temperature tend to zero.
Optimizing the "Chair" and "Boat" Transition States
As explained above, the Cope Rearrangement can either go though a "Chair" Cyclohexane Transition State (Chair TS) or a "Boat" Cyclohexane Transition State (Boat TS). In order to find out which of the two possible transition states the Cope rearrangement processed by, the energies of the two possible transitions states have to be found and compared. There is a number of ways that the possible transition state can be optimized in order to find the energy of their lowest energy confirmations and these are demonstrated below.
The first method is to build a structure that is approximately like the predicted transitions state and then optimise its structure as a transition state calculating the force constants in the molecule once, knowing that a transition state has one imaginary frequency (negative frequency on a vibration spectrum). This method was used to find the optimized structure Chair TS. This done by first making an approximate structure of the Chair TS out of two CH2CHCH2 molecules which had been optimised to their lowest energy confirmations using the Hartree-Fock calculation method and the 3-21G basic set of orbitals. These two molecules were positioned to approximate the Chair TS as shown in the Jmol below:
This structure was then optimised, but not to minimum, but to TS (Berny). This was done again using the Hartree-Fock calculation method and the 3-21G basic set. The vibrational spectrum was also calculated using the same method and basic set. I order to decrease the chance of calculation failing and giving an error message, in the additional word section of the calculation set up, "Opt=NoEigen" was typed; this stops the calculation failing if a second negative frequency is calculated for a particular confirmation when the calculation is trying to find the optimized Chair TS structure. The resulting structure for the chair TS is shown below:
Another method similar to the optimisation method above, is the "freeze coordinate" method. Again, the approximate structure for the Chair TS as shown above was used, but this time instead of calculating force constants in order to optimise the Chair TS structure to it lowest energy confirmation, the distance between the two pairs of terminal carbons were frozen. The structure was then optimized to its minimum confirmation, using the Hartree-Fock method and the 3-21G basic set. The resulting structure is completely optimized apart from the two bonds that are forming/breaking. This structure was then used to calculate the structure of the Chair TS by optimising the two bonds that are forming/breaking. This was done by performing an optimisation on the structure to TS (Berny) telling the calculation to derive the bond lengths between the two pairs of terminal carbons. This was done using again the Hartree-Fock method and the 3-21G basic set. Instead of calculating the force constants in the calculation as was done above in the first method to find the optimised structure of Chair TS, a normal guess Hessian method is used to gain information about the positions of the terminal carbons. The resulting structure of this optimisation for the structure of Chair TS was the same as the structure shown above. Shown below is a table comparing the results of the two types of optimisations for the lowest energy confirmation of Chair TS:
| Force Constant Method | Freeze Coordinate Method | |
|---|---|---|
| Energy (Hartrees) | -231.6193 | -231.6193 |
| Gradient on the Energy Surface (Hartrees) | 0.000030 | 0.000019 |
| Sum of Electronic and Zero Point Energies (0K) | -231.4667 | -231.4667 |
| Sum of Electronic and Thermal Energies (298K) | -231.4613 | -231.4613 |
It can be seen that both methods give the same energy values and agree with each other, showing that both methods are valid and can be used.
The Boat Transition state for the Cope rearrangement was found by using a different method called the QST2 method. This involves telling the calculation the reactant and the product for the reaction and then the calculation finds the transition point between the two molecules. Below is given the reactant and product for the Cope Rearrangement based on the Anti 2 confirmation of 1,5 Hexadiene.


A QST2 Transition state optimisation calculation was then run, using the Hartree-Fock calculation method and the 3-21G basic set. The resulting transition state structure is shown below:
It can clearly be seen that this transition state optimisation has failed to give the desired Boat transition state. Therefore the QST2 optimisation calculation was tried again using the Hartree-Fock calculation method and the 3-21G basic set again, but this time the confirmation of the reactant and product were changed as seen below:


The resulting transition structure for this calculation is shown below:
It can be seen that this has a structure close to the Boat confirmation of cyclohexane and is the Boat TS for the Cope rearrangement. Below is given some of the calculated energy data:
| Energy (Hartrees) | -231.6028 |
| Gradient on the Energy Surface (Hartrees) | 0.000011 |
| Sum of Electronic and Zero Point Energies (0K) | -231.4509 |
| Sum of Electronic and Thermal Energies (298K) | -231.4452 |
To insure both the Chair and the Boat transition states for the Cope rearrangement had been found successfully, the vibrations of the molecule were looked at. It is known that a transition state should have one vibration at a negative frequency and that the motion of this vibration should be the motion of the bonds forming/breaking in the reaction. The motion of the negative frequency in both the Chair TS and the Boat TS are shown below, and show that these are the correct Chair TS and Boat TS:
| Transition State | Frequency | Vibration |
|---|---|---|
| Chair | 817.98cm-1 | 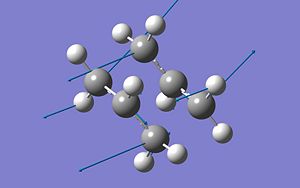
|
| Boat | 840.00cm-1 | 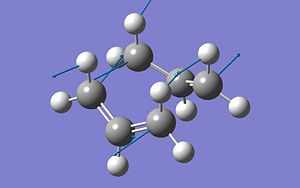
|
The two transition states have been found, but it is unknown which of the confirmations of 1,5 Hexadiene is required for a Cope rearrangement to occur to reach one of these two transition states. As mentioned above, it is predicted that the confirmation is the Anti 2 confirmation, but this needs to be proved. This can be found by doing an Intrinsic Reaction Coordinate (IRC) calculation. This done for both of the transition states, calculating the force constant once in the transition state. The IRC was also only calculated in one direction, due to the fact that the reaction was symmetrical (Product are the same as Reactants). It would be calculated in both directions if a rearrangement resulted in the reactants being different from the products. The result of these calculations are shown below, as well as the confirmation of 1,5 Hexadiene found by these calculations:




File:Chair101.molFile:Boat101.mol
Note. Chair TS Reactant is the confirmation of 1,5 Hexadiene shown to be required by for a Cope rearrangement to go though a Chair transition state, where as the Boat TS Reactant is the confirmation of 1,5 Hexadiene shown to be required by for a Cope rearrangement to go though a Boat transition state. Also, it can be seen that there is an anomaly point on the IRC as calculated for the Chair TS due to the calculation failing.
It can be seen from the graphs above and the confirmations of 1,5 Hexadiene that the optimisation of the reactant for the Cope rearrangement has not complete to give a minimum energy confirmation of the reactant. This is suggested by the fact that on the both the IRC graphs (Boat TS and Chair TS IRCs) they do not reach a minimum (energy) point and the gradient on both IRCs does not reach zero (and the gradient at a minimum (energy) point is always zero). Therefore, two methods were tried in order to try to find the minimum energy confirmations for the reactant of the Cope rearrangement to result in a Chair TS and Boat TS. The first was to take the last confirmation of 1,5 Hexadiene given on both the IRCs and to optimise them to their lowest energy confirmation using the Hartree-Fock calculation method and the 3-21G basic set. The second method was to run the IRC calculation again, but this time to calculate the force constants at every step in order to find the confirmation of 1,5 Hexadiene require to under go a Cope rearrangement via a Chair TS or a Boat TS. Both these method gave very similar structure for the confirmation of 1,5 Hexadiene required for a Cope Rearrangement to occur via a Chair TS and a Boat TS and these confirmations are shown below, along with the IRC graphs when calculating the force constant a every step:




File:Chair102.molFile:Boat102.mol
Note. Chair TS Reactant 2 is the confirmation of 1,5 Hexadiene shown to be required by for a Cope rearrangement to go though a Chair transition state as found by the method described above, where as the Boat TS Reactants the confirmation of 1,5 Hexadiene shown to be required by for a Cope rearrangement to go though a Boat transition state as found by the methods above.
It can be seen that the confirmation of 1,5 Hexadiene required to under go a Cope rearrangement via a Chair TS is the Anti 2 confirmation. It can also be seen that the confirmation of 1,5 Hexadiene required to under go a Cope rearrangement via a Boat TS is very similar in confirmation to the Anti 2 confirmation of 1,5 Hexadiene, showing the prediction that the confirmation of 1,5 Hexadiene required to under go a Cope rearrangement is the Anti 2 confirmation is valid.
Knowing the confirmation and energy values of the reactant (Anti 2) and the confirmation and energies of the two possible transition states (Chair TS and Boat TS), it possible to predict which of the two transition states the Cope rearrangement will precede by and the energy changes going from the react to the two possible transition states. This is shown in the table below, along with the energies for the Chair TS and Boat TS when calculated using the B3LYP calculation method and 6-31G d basic set in order to compare the calculation method/basic set combination results:
| Electronic Energy (HF 3-21G) | Sum of Electronic and Zero-point Energies at 0K (HF 3-21G) | Sum Electronic and Thermal Energies at 298K (HF 3-21G) | Electronic Energy (B3LYP 6-31G d) | Sum of Electronic and Zero-point Energies at 0K (B3LYP 6-31G d) | Sum Electronic and Thermal Energies at 298K (B3LYP 6-31G d) | |
|---|---|---|---|---|---|---|
| Chair TS | -231.6193 | -231.4667 | -231.4613 | -234.5589 | -234.4170 | -234.4090 |
| Boat TS | -231.6028 | -231.4509 | -231.4452 | -234.5450 | -234.4045 | -234.3960 |
| Anti 2 (Reactant) | -231.6925 | -231.5395 | -231.5325 | -234.6117 | -234.4692 | -234.4619 |
| HF 3-21G at 0K | HF 3-21G at 298K | B3LYP 6-31G d at 0K | B3LYP 6-31G d at 298K | Experimental at 0K2 | |
|---|---|---|---|---|---|
| Chair TS and Reactant | 45.68 | 44.68 | 31.06 | 33.17 | 33.5 |
| Boat TS and Reactant | 55.60 | 54.78 | 41.85 | 41.32 | 44.7 |
Note: 1 Hartree = 627.509 kcal/mol. HF reference to the Hartree-Fock calculation method. Energy difference found between Sum ok Electronic and Zero-point Energies for 0K and the Sum Electronic and Thermal Energies for 298K
It can be seen that the energy difference is less between the reactant and the Chair TS compared to the reactant and the Boat TS, suggesting that the Cope rearrangement goes though a Chair Transition state. It can also be seen that the calculations and the resulting energy difference for the more complex B3LYP 6-31G d calculation/basic set combination are closer to what is seen experimentally compared to the Hartree-Fock 3-21G calculation/basic set combination.
The Diels Alder Cycloaddition
Cis-butadiene reaction with ethene
Consider the Diels Alder Cycloaddition reaction below:

It can be seen that for this reaction to occur, there must be good orbital overlap between the pi-orbitals on both the cis-butadiene and the ethene molecule and that the phase of the orbital lobes interacting must be the same (positive to positive, negative to negative). For this to happen, the symmetry of the molecular orbitals interacting (HOMO and LUMO) on the two molecules must be the same with respect to the plane run down the molecule. To find the shape the molecular orbitals of molecules and hence find their symmetry, computer calculations can be done when the structure of the molecule is being optimized (as shown above) and will give the shape of the molecular orbitals. Below is given the HOMO and LUMO for Cis-butadiene and Ethene:




From the molecular orbitals above, it can be seen that both LUMO of Cis-butadiene and HOMO of Ethene are symmetry with respect to a plane perpendicular to the carbon-carbon single in the former and the carbon-carbon double bond in the latter and it can also be seen that these orbitals could overlap with the correct phases and, as it is a HOMO and LUMO overlapping, the chemical reaction above could occur. The same is true if considering the HOMO of the Cis-butadiene and the LUMO of the Ethene. Both of these orbitals are anti-symmetric with respect to the same plane described above and they can overlap with the same phase, allowing the reaction above to take place. However, one of these two pairs of molecular orbitals (LUMO of Cis-butadiene/HOMO of Ethene and HOMO of Cis-butadiene/LUMO of the Ethene) will form the HOMO of the transition state of this reaction and the other pair will form the LUMO of the transition state of this reaction and it can not be known which pair will result in which molecular orbital in the transition state from the information above. Knowing which molecular orbitals in the reactants results in which molecular orbital in the transition state is important as in reaction where more than one isomer can form, this information may help determine which product will predominate by considering the orbital overlap between reactants and in the transition state.
In order to answer the question posed above (which reactant orbitals results in which orbitals in the transition state of the Diels Alder reaction given above), first the confirmation of the transition state has to be found. This was done by building a structure in the computer interface which was thought to be close to that of the transition state and then this structure was optimised to a TS Berny, using the AM1 Semi-Empirical calculation and calculating the force once. The resulting structure is shown below:
To confirm that the correct structure had been calculated for the Diels Alder transition state, it was checked that there was one negative frequency and that the motion of this frequency was formation of the bonds shown to be make in the Diels Alder reaction scheme above. It was found that there was one negative frequency occurring at -956.23cm-1 and this is shown below:

This vibration above does shown the formation of the bonds seen to be forming the reaction scheme of the Diels Alder cycloaddition seen above and confirms the fact that the correct structure of the transition state has been calculated. The vibration given above also provides other information. It can be seen from the vibration above that both the bonds forming are forming at the same time, the bonds form synchronous. The bond forming vibration can also be compared to the lowest positive frequency vibration to see if they are similar. The lowest positive frequency vibration occurs at 147.29cm-1 and is shown below:

It can be seen that this vibration is a bending type of vibration, unlike the bond forming vibration which a stretching vibration. It can seen when comparing the two vibrations, the bond forming vibration is symmetric (hence why the bonds form synchronous) and the displacement vectors for the bond forming vibration are large compared to the lowest positive frequency vibration which is anti-symmetric (so if this was the bond forming vibration, the bonds would form asynchronous) and the displacement vectors for the vibration are small.
Below is given a table of bond lengths seen in the transitions state of the Diels Alder reaction:
| Bond | Bond Length |
|---|---|
| C-C Forming | 2.12Â |
| C=C Breaking (Double bond breaking in Cis-Butediene) | 1.38Â |
| C=C Forming (Double bond forming) | 1.40Â |
Considering the C-C forming bond lengths in the transition state, it can be seen that it is longer than a normal C-C single bond (1.531Â at a sp3 carbond and 1.47 at a sp2 carbon3) but shorter than 2x Van der Waals radius of carbon (Van der Waals radius of carbon = 1.70Â). A bond/interactions between atoms is consider to occur when the distance between the two atom is less than their combinde Van der Waal radius. Therefore, it can be seen the transtion state of the Diels Alder reaction that the new c-c single bonds have not formed yet, otherwise the distance between the two atoms would be shorter, but the end carbon atoms are within each others Van der Waals radius and are interacting and this is what is expected to be seen by the distance between the carbon atoms forming a C-C single bond (during the reaction) in the transition state.
Using the optimised structure of the transition state, it is possible to find the shape of the HOMO and LUMO of the transition state. These are shown below:


It can be observed from the molecular orbitals above for the transition state that the HOMO is anti-symmetric (with regards to a plane perpendicular to the carbon-carbon double bond) and is formed from the HOMO of the cis-butadiene and the LUMO of the ethene and that the LUMO is symmetric and is formed from the LUMO of cis-butadiene and the HOMO of the ethene. As explained above, these MO for the transition state can form, allowing the reaction to take place, due to the good overlap between the molecular orbitals of the reactants and the fact that when the orbitals overlap they are all of the same phase in both cases.
Cyclohexa-1,3-diene reaction with Maleic Anhydride
Considering the reaction shown below, it is known that one of two product could be formed, either a exo or endo product:
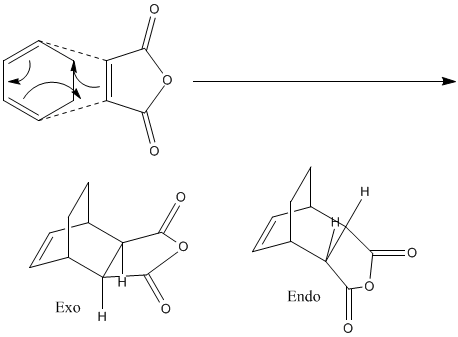
It is known that the exo product is lower in energy, but the major product of this reaction is the endo product. This suggests that this reaction is under kinetic control and that the energy of the transition to the endo product is lower than the transition state leading to the exp product.
In order to investigate whether the exo transition state (Exo TS) is higher in energy than the endo transition (Endo TS) state and to explain why this might be the case, an approximate structure of both the possible transition states were built into the computer interface and were optimised to TS Berny, calculating the force constants once and using the AM1 Semi-empirical calculation method. The resulting structures of the transition states are shown below:
File:DATS Exo.molFile:DATS Endo.mol
The main structural difference between the Exo TS and the Endo TS is that in the Exo form the-C(O)-0-C(O) group in the maleic anhydride is opposite a -CH2-CH2- in the cyclohexadiene ring and in the Endo TS the -C(O)-0-C(O) group in the maleic anhydride is opposite a -CH=CH- in the cyclohexadiene ring and this structural difference is important when considering the energy difference between the two transition states.
As normal, the transitions states were checked to be in the correct confirmation by checking they had one negative frequency that had a motion relating to the bonds forming in the reaction. These two negative frequencies (one for each transition state) are shown below, along with the frequency which they occur at:


It can be seen that the negative frequency found for each of the transition states does correspond to the bond forming process seen in the reaction scheme above, confirming that the correct structures for the two transition states had been found. The two transition states were further optimised by optimising to TS Berny and calculating the force constants once, but using the Hartree-Fock calculation method and 3-21G basic set and using the B3LYP calculation method and the 6-31G d basic set. The energies found by these three methods are shown below:
| Energy Term | Exo TS | Endo TS |
|---|---|---|
| Sum of Electronic and Zero Point Energies | 0.1349 | 0.1195 |
| Sum of Electronic and Thermal Energies | 0.1449 | 0.1298 |
| Total Energy | -0.0504 | -0.1298 |
| Energy Term | Exo TS | Endo TS |
|---|---|---|
| Sum of Electronic and Zero Point Energies | -605.4240 | -605.4331 |
| Sum of Electronic and Thermal Energies | -605.4145 | -605.4236 |
| Total Energy | -605.6190 | -605.6281 |
| Energy Term | Exo TS | Endo TS |
|---|---|---|
| Sum of Electronic and Zero Point Energies | -612.5105 | -612.5163 |
| Sum of Electronic and Thermal Energies | -612.5001 | -612.5059 |
| Total Energy | -612.6915 | -612.6972 |
The data in the tables above confirm the fact that the transition state leading to the Exo product is higher in energy than the transition state leading the Endo product, explaining why the Endo product is seen as the major product of the reaction, as this reaction is under kinetic control. However, these results do not explain why the Endo TS is lower in energy than the Exo TS.
One characteristic which many explain the energy difference between the Exo TS and the Endo TS is the bond lengths and the distance between the O=C-O-C=O unit and the -CH2-CH2- unit in the Exo TS and the distance between the O=C-O-C=O unit and the -CH=CH- unit in the Endo TS (These 2 lengths will be called length x). The last distance described, length x, is important as it is the distance between the two large groups and so the shorter the distance between them, the greater the steric slash, causing the energy of transition state to increase. The distance for these lengths for both the Exo TS and Endo TS are shown below for the different calculation methods and basic sets:
| Structural Parameter | Exo TS | Endo TS |
|---|---|---|
| Length x | 3.34Â | 3.31Â |
| C-C Forming bond length | 2.17Â | 2.17Â |
| C-OC Bond length | 1.41Â | 1.41Â |
| C=C Bond length (Double bond braking) | 1.39Â | 1.39Â |
| C=C Bond length (Double bond forming) | 1.40Â | 1.40Â |
| Structural Parameter | Exo TS | Endo TS |
|---|---|---|
| Length x | 3.32Â | 3.10Â |
| C-C Forming bond length | 2.27Â | 2.30Â |
| C-OC Bond length | 1.40Â | 1.40Â |
| C=C Bond length (Double bond braking) | 1.37Â | 1.39Â |
| C=C Bond length (Double bond forming) | 1.40Â | 1.40Â |
| Structural Parameter | Exo TS | Endo TS |
|---|---|---|
| Length x | 3.35Â | 3.26Â |
| C-C Forming bond length | 2.30Â | 2.27Â |
| C-OC Bond length | 1.40Â | 1.40Â |
| C=C Bond length (Double bond braking) | 1.39Â | 1.39Â |
| C=C Bond length (Double bond forming) | 1.40Â | 1.40Â |
From the tables above, it is suggested that there is more steric hinderance in the Endo TS than in the Exo TS. This is shown by the fact that the distance between two large groups decribed above (Length x) is shorter in the Endo TS according to all the calculation methods than in the Exo TS. This would suggest that the Endo TS should be higher in energy, but this is not the case and the Exo TS is higher in energy. However, it can be seen in the Exo TS, two hydrogen atoms point towards the -C(O)-O-C(O)- group; the distance between them is 2.42Â as calculated by the AM1 Semi-emprical method. It is possible that there could be a sterc interaction between them, raising the energy of the Exo TS.
Another factor that might effect the energy of the Exo TS and the Endo TS is the molecular orbitals. The HOMO for both the Exo TS and the Endo TS are shown below:


It can be obseved that the HOMO in both transition states are very similar and no strong secondary molecular overlap, although in the HOMO of the Endo TS, it can be seen there is possible overlap between the orbital on the -C-O-C- and the -CH=CH- orbital, although if this was a strong overlap, the molecular orbital would be continuous. It is unknown how much this potenital overlap would effect the energy of the Endo TS and further calculation with more complex methods and basic sets need to be done in order to assess whether there is or is not an orbital overlap between the orbitals mentioned and the effect of this. Here it is assumed that it has little effect on the energy of the Endo TS and therefore, the HOMO for the Exo TS and the Endo TS shows very little secondary molecular orbital overlap and so the energy difference of the two transition state is most likely to be due to steric interactions between the two hydrogens on the cyclohexadiene and the -C(O)-O-C(O)- on the Maleic Anhydride, causing the Exo TS to be higher in energy than the Endo TS, as decribed above.
The Claisen Rearragement
Following on from the investigation into whether the Cope rearragement processed though a "Boat" or a "Chair" like transition state, it was investigated whether the Claisen Rearragement also processed though a Chair transition state, as the Cope rearragement does. Below is give the reaction scheme of the Cope rearragement:

In order to investigate this, an approximate structure of the two possible transition states (Boat TS and Chair TS) were built into the computer interface and then optimised to TS Berny, calculating the force constants once and using the Hartree-Fock calculation method and the 3-21G basic sets
The resulting structure for the two transition states are shown below:


File:Chair Claisen1.molFile:Boat Claisen1.mol
The transition states were checked to be correct by checking they each has one negative frequency relating to the bond forming/breaking process seen in the reaction. This was seen to be the case and are shown below along with their frequency:


The energy of two transition states were found to be -267.2366 Hartree for the Boat TS and -267.2386 Hartree for the Chair TS. This suggests that the Claisen rearragement processeds through the lower energy Chair TS.
A IRC was also run on the two transition states. This was done by calculating the force constants once, using the Hartree-Fock calculation method and the 3-21G basic set. However, unlike for the Cope rearragement, this was done for both directions of the reactions, as the products are different from the reactants. The results of this are shown below for both the Chair TS and the Boat TS:




Note: It can be seen that there are anomaly results seen in these IRC graphs and that also the IRC has not fully completted as the gradient has not gone to zero and so further calculations should be done by either optimising the reactants/products in their minimum or by calculating the IRC calculating the force constants at every step.
The IRC graphs shows that the Claisen rearragement is not in equilibrium, as it can be seen that the products and reactants are at different energies. This would result in all the reactant molecules becoming product molecules with a C=O double bond in them. Below is shown the structures of the reactants and products, with their approximate energies:


The reason why the product molecule is more stable than the reactant molecule is most likely due to the formation of the C=O double bond in the product and the formation of this bond is thermodynamically favourable.
Below is a table of the energies of the Chair TS and Boat TS:
| Energy Term | Chair TS | Boat TS | Reactant |
|---|---|---|---|
| Sum of Electronic and Zero Point Energies | -267.1119 | -267.1106 | -267.1119 |
| Sum of Electronic and Thermal Energies | -267.1066 | -267.1051 | -267.1672 |
| Total Energy | -267.2566 | -267.2386 | -267.3000 |
This information can be used to find the experimental activation from the reactant to the two transition states, using the same method as used for finding the energy differences between the reactant the transition state for the Cope rearragement. This is shown below:
| HF 3-21G at 0K | HF 3-21G at 298K | |
|---|---|---|
| Chair TS and Reactant | 39.09 | 38.03 |
| Boat TS and Reactant | 39.91 | 38.96 |
It can be seen that the Chair TS is lower in energy than the Boat TS and this suggests that the Claisen rearragement will go via a Chair transition state. It is also seen that activation energy for the Chair TS is lower than the activiation energy for the Boat TS by approximately 1 Kcal/mol, a much smaller difference than what is seen between the Chair TS activiation energy and the Boat TS activation fo the Cope Rearragement, which is about 10 Kcal/mol. In general though the activation energies seen here are similar to what is seen for the Cope rearragement, although they are smaller than the values found using the same calculation and basic set for the Cope rearragement, suggesting that the Claisen rearragement will be a kinteically faster reaction than the Cope rearragement at the same set of reaction conditions.
References and Data
Cope Data
File:Chair Guess opt f).out IRC for Chair TS calculating force constants once
File:Boat f) Reaction.out IRC for Boat TS calculating force constants once
File:Chair Scan Reaction.out IRC for Chair TS calculating force constants at each step
File:Boat Scan Reaction.out IRC for Boat TS calculating force constants at each step
Diels Alder Data
File:TS2.out Optimising the first Diels Alder transition state using AM1
File:TS 2 HF.out Optimising the first Diels Alder transition state using Hartree Fock
File:Exo.out Optimising the Exo TS using AM1
File:Endo.out Optimising the Endo TS using AM1
File:Exo HF 3-21G.out Optimising the Exo TS using Hartree Fock
File:Endo HF 3-21G.out Optimising the Endo TS using Hartree Fock
File:Exo B3LYP 6-31G d.out Optimising the Exo TS using B3LYP
File:Exo B3LYP 6-21G d.out Optimising the Endo TS using B3LYP
Calisen Rearragement Data
File:Chair Claisen.out Optimsing the Chair TS for the Claisen rearragement
File:Boat Claisen.out Optimising the Boat TS for the Claisen rearragement
File:Chair Claisen reaction.out IRC for Chair TS
File:Boat Claisen reaction.out IRC for Boat TS
References
1) Tee, O.S. and Yates, K., J. Am. Chem. Soc., 1972, 94, 9, 3074
2) http://www.ch.ic.ac.uk/wiki/index.php/Mod:phys3
3) CRC Handbook of Chemistry and Physics, 90th ed, 2009