Rep:Mod:TomTaylorMod2a
Computational Inorganic Chemistry Lab
Investigating the confirmation and vibrations of BH3 and BCl3
The structure of both BH3 and BCl3 were both built in GaussView and then the structure of both these molecules were optimised to find the energy of the lowest energy confirmation. This was done by solving the Schrödinger equation using Gaussian. Due to the fact that both BH3 and BCl3 are diatomic molecules, for Gaussian to solve the the Schrödinger equation approximation have to be made. First, it is assumed that the nucleus is very slow compared to electrons and so is assumed to be stationary. This is the Born-Oppenheimer approximation. The second approximation is that the molecular orbitals can be built up of a "basic set" of orbitals. This basic set of orbitals is based on the atomic orbital of Hydrogen. Different "levels" of basic sets can used, resulting in different levels of accuracy of the calculation. Other approximations are also made depending on the calculation method used. For the optimisation of BH3 and BCl3 the calculation method used was the B3LYP for both molecules and the basic set of orbitals used for BH3 was the 3-21G set and the LANL2MB basic set was used for BCl3. The 3-21G set is very simple set of orbitals, were as the LANL2MB basic set is more complex basic set and is required due the large chlorine atoms present in BCl3. However, as the approximations are very basic and the molecules are not very large, the calculations are very quick, but may not be very accurate due to the approximations and basic sets of orbitals. The results of these calculations are shown below (Energies given in atomic units where 1 a.u. = 2625.5KJ/mol):
| BH3 | BCl3 | |
|---|---|---|
| Calculation Type | FOPT | FOPT |
| Calculation Method | RB3LYP | RB3LYP |
| Basis Set | 3-21G | LANL2MB |
| Energy (RB3LYP) | -26.46 a.u. | -69.44 a.u. |
| Gradient | 0.0002 a.u. | 0.00006 a.u. |
| Time taken for calculation | 21 seconds | 6 seconds |
The error on the energy value is 10KJ/mol or 0.0038 a.u. The structures of both molecules are shown below:
File:BH3 Opt.molFile:BCl3 Opt.mol
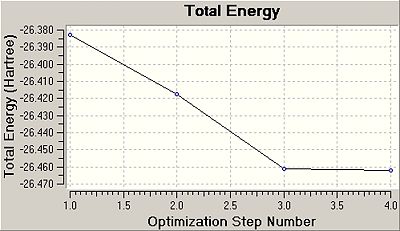
In order to calculated the lowest energy confirmation of the molecule and solve the Schrodinger equation, the computer takes "guesses" at the wave function of the molecules, improving the guesses of the wavefuction until it has found the minimum energy and a point on the energy surface which the gradient is zero (and thus is a stationary point, which a minimum point has to be). This is the gradient value given in table 1. Below is shown graphs of how the computer make guess and improvement on the wavefuction, resulting in the minimum energy confirmation and zero energy:
It can be seen that both of these molecules have the expected trigonal planar structure and have the expected D3H point group. The calculation also predicted characteristics of the Molecules correctly, such as the fact that both molecules do not have a dipole (all the dipoles on the molecules cancel each other out). It can been seen that these calculations were very quick, although the more complex BCl3 was quicker calculation, this is due to the fact that the point group (D3H) was inserted for the calculation of BCl3 resulting in the calculation being more accurate and quicker. As mentioned above, for the BH3 molecule, the calculation showed the point group to be D3H, even though it was not inserted into the calculation. This is most likely due to how the structure was built into Gaussview had symmetry close to that of the D3H point group. Therefore, even though the symmetry used for the calculation was C1, Gaussian "saw" the symmetry of the molecule and used this symmetry to optimise the structure of BH3 and hence why the resulting point group is the expected D3H.
It should be noted that energies found are not linked to the Gibbs energies of the molecules or any other thermodynamic quantity linked to the molecules and are only used to make sure calculations are repeatable and that the same findings can be found by others. It was also possible to compare the optimised structure (as calculated) of both these molecules to what is seen experimentally. This is shown below:
| Calculation | Experimental1 | |
|---|---|---|
| B - H Bond Length | 1.19 Â | 1.19 Â |
| H-B-H Angle | 120O | N/A |
| B - Cl Bond Length | 1.87 Â | 1.73 Â |
| Cl-B-Cl Angle | 120O | 120O |
It can be seen that the calculated and experimental results are very close to each other, showing that the calculation method and bases set used for both molecules were appropriate. Unfortunately, no experimental angle could be found for H-B-H in BH3, it is assumed this is due to be because BH3 forms dimmers very easily. It can also safely be assumed that the experimental angle will be or close to 120O. In table 1, the gradient values are given for the point on energy surface which the energy of the optimised confirmation occurs at. It is known that the optimised structures energy should be a minimum (stationary) point on the energy surface. This means that if the bonds were either stretched, compressed or the angle between them was changed, the energy of the molecule would increase. It is known that at any stationary point the gradient of the energy surface should be close to zero. From table 1, it can be seen for both BH3 and BCl3, this is the case, with the gradient values being close to zero. However, the gradient doesn't itself tell us whether the energy surface is at minimum; it only tells us the energy surface is at stationary point. In order to determine whether the stationary point is a minimum point, the 2nd devrived has to be found and has to be negative. This can be done by performing a frequency calculation on the optimised confirmation of the molecule and this is what is done for both BH3 and BCl3. If all the peaks on the spectrum are at positive frequencies (cm-1), the confirmation is the minimum energy confirmation for that molecule, one negative frequency represents a transition state and more than one negative frequency shows that the molecule has not been optimised to its lowest energy confirmation correctly. In order to do this frequency calculation, it is critical that the both the same method (RB3LYP) and same bases sets (3-21G for BH3 and LANL2MB for BCl3). This is due to the fact that each combination of bases sets and calculation method will result in slightly different lowest energy confirmations, due to the different methods and approximations used in the calculations. If the method used for the optimisation calculation and frequency calculation are different, it would show on the frequency spectrum negative peaks, even though it is highly probable that the molecule is in the lowest energy conformation for the method and basics set used in the optimisation calculation. Therefore, a frequency calculation is performed in order to test whether a molecule is in the lowest energy confirmation for the method and bases set used in the optimisation calculation, the same method and bases set have to be used in the frequency calculation. The results of this for both BH3 and BCl3 are shown below:
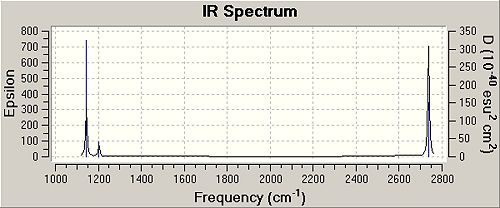

For both of these spectrum, it can been seen that there are no vibrations at negative frequencies, showing that both BH3and BCl3 have been optimised to their minimum energy confirmation. However, if instead of looking at results-vibrations, the data file was taken as the results of the calculation (results-view file), it can be see that there are 6 vibrations not shown on the vibration spectrum which occur at between 0 - -67cm-1 for BH3 and between 0 - -8cm-1 for BCl3. This would suggest that the optimisation has not worked, as more than one peak at negative frequency shows this. However, this is not the case. These frequencies are for other motions, not vibrations. This comes from the fact that each molecule has 3N-6 vibrations and these 6 frequencies represent the "-6" bit of 3N-6. Also from the frequency calculations, it is possible to view the vibrations that cause the frequencies seen on the vibration spectrums. This is shown below for BH3 in table 3:
From the table above, it can be seen that there 6 vibrations possible, but vibrational spectrum for BH3 only shows 3. The reason why the number of vibrations shown on the vibration spectrum is due to two reasons. First, one of the vibrations (2498cm-1) does not result in an change in the dipole and there fore has an intensity of of zero ca not be seen. The other two vibrations that cannot be seen on the vibration spectrum is due to the fact they are degenerate to another vibration and so appears at the same frequency. So, the peaks at 1203cm-1 and 2737cm-1 represent 2 vibrations and explains why there are not more peaks for these vibrations on the the spectrum.
It was noted that whilst doing these calculation for the optimisation and calculating the frequencies of both BH3 and BCl3, often when the calculation can back with the structure of the molecule, often the bonds would be missing. The reason for this is that GaussView has a set length for chemical bonds between two atoms and if a calculation shows that the distance between two atoms is less than the length it considers should be between the two atoms for a bond to exist, GaussView puts a bond in. If however, the distance between two atoms is longer than the length GaussView considers there needs to be for a chemical bond between the two atom, Gaussview considers there to be no bond, even though experimentally there may be a bond between the two atoms. The fact that GaussView considers that the bond between two atoms to be a set value is a weakness of these calculations; GaussView doesn't take into account other factors, such as the atoms involved in the bond (GaussView is set up for shorter organic bonds) and the surrounding atoms. It only considers distance between atoms as the key factor is a bond exists or not.
This leads to the discussion on what a chemical bond exactly is. On diagrams, bonds are represented by lines between atoms, although in actual fact there is no "structure" in bonds; if it was possible to look between two bonded atoms, nothing would be seen between the two atoms. A chemical bond can be considered to be the attraction between two atom caused by opposite and attracting electromagnetic forces resulting in a rigid location of one of the atoms with respected to the other. However, although this description is good for covalent bonds (two atoms sharing electrons) and would be able to define the bonding seen in the optimisations performed above, it doesn't describe ionic bonding very well, due to the fact that in ionic bonding one atom becomes fully negatively charged and the other full positively charged by exchanging electrons and that in solutions there is not "structure" to this bonding; none of the atoms stay in the same location with respect to another atom. This description would also consider intramolecular forces, such as Van der Waal forces and H-bonds as possible bonds, although these are not considered as bonds in the same sense as a Covalent bond; there has to be a set amount of electronic interaction for there to be a bond that chemists would represent as a line on a chemical diagram. There are also molecules, such as metal complexes, where in a chemical diagram two groups would be bonded, but experimentally, these groups are rapidly exchanging with other molecules. This is the problem, how much electronic interaction and how rigid should the location of the two atoms to each other need to be for a line to be draw to represent a bond? This is why GaussView uses the crude assumption that all atoms with less than a certain distance between them most be bonded, over that length, no bond.
As well as performing a calculations to predict the vibrational spectrum of BH3 and BCl3, calculations were performed to give the predicted Molecular Orbitals (MO) diagram of BH3 and the energies of the energy levels in the MO diagram. Below is shown the predicted MO diagram of BH3 using linear combination of atomic orbitals (LCAO) MO theory with the predicted shapes of the MOs by both LCAO theory and by the calculations performed here. LCAO theory is the theory that the shape of the molecular orbitals can be approximated by considering the shapes of the atomic orbitals that are going to combine to give the MO. Also shown is a table of the relative energies of the MOs:

| MO | Relative Energy |
|---|---|
| 2a'1 | -0.518 |
| 1e' (2 MOs) HOMO | -0.357 |
| 2a2 LUMO | -0.074 |
| 3a'1 | 0.192 |
| 2e' (2 MOs) | 0.189 |
Note: 1a'1 is the 1s atomic orbital on the boron atom. From the data above, it can be seen that both the calculations and LCAO theory predict very similar shapes for the MOs. Although there are some differences between the shapes of the MOs predicted by the two methods, it is clear which of the MOs predicted by the LCAO theory matches the respective Mo predicted by the calculation. Therefore, it is observed that LCAO theory of considering the shapes of the atomic orbitals before they combine to give the MO is a useful and accurate prediction when considering the shapes of the MOs and is simple and require no calculation to do. When considering the relative energies of the MOs, there is a slight difference in the ordering of the MOs. LCAO theory predicted that the two 2e' MOs are highest in energy, followed by 3a'1 MO, where as the calculations performed here suggests that 3a'1 MO is highest in energy, then the 2e' MOs. When looking at the relative energies that have been calculated, it can be seen that the 3a' and 2e' MOs are very close in energy. The reason why it’s difficult to predict which of 3a' and 2e' energy levels are higher in energy using LCAO is due to the difficulty in evaluating whether the stronger s-s mixing in 3a'1 (resulting in a higher 3a'1 MO) or the fact the e' atomic orbitals used to make 2e' MOs are higher in energy than the a'1 used to form the 3a'1 (resulting in higher energy 2e' MOs) has a larger effect. The calculation here predict the s-s mixing has a larger effect, resulting in the anti-bonding 3a'1 MO being highest in energy.
Also, a calculation was performed to produce a diagram of the charge density of BH3. This is done by performing a natrual bond orbital (NBO) anaylsis on BH3. This is shown below:

Knowing that green represents highly positive and red represents highly negative, it can be seen that the boron atom is highly positive, which fits with experimental data for BH3, that it is a electron deficient compound and is a strong Lewis acid, readly accepting electrons.
Cis and Trans Isomerism of a Organometallic Compound
In this sections of the report, calculations will be performed in order to calculate the thermal stabilities of Cis-[Mo(PPh3)2(CO)4] (Cis) and Trans-[Mo(PPh3)2(CO)4] (Trans), as well as predict their vibrationsal spectrums and vibrationsal modes. However, both of these molecules are very computational demanding to calculate, mainly due to the PPh3 group. In order to simplify the calculation, the PPh3 groups are replaced by PCl3 groups. This is due the fact that the -Cl atoms are seen to be electronically similar to -Ph groups and are a lot easier to compute.
In order to find out which of the two isomers are the most thermally stable, first the structures of both isomer have to optimised to find the lowest energy confirmation for each of the isomers and the energies of these. This was done in a number of steps in order to insure that the optimisations of the molecules are as accurate as possible. To start, both molecules are optimised using the B3LYP method and using the LANL2MB basis set and pseudo-potential. This was done using done using the additional key words "opt=loose". This done to insure that this first calculation converges or the calculation may take a long time or fail due to not reaching the converges limit. After this optimisation was completed, minor manual edits were made to the structure. This consisted of changing the dihedral angle between the chlorine atoms and the carbon atoms in the carbonyl groups for the Cis complex and ensuring the PCl3 are eclipsed in the Trans complex. This done to make sure that when further optimisations are done, the resulting structure is representative of the true lowest energy confirmation, not a local minimum energy confirmation on the energy surface. It is known that the lowest energy confirmations of both of these complexes have the PCl3 arranged as explained above. If was not know, optimisations would have to be done on a range of confirmations of the PCl3 groups in each of the molecules in order to find the lowest energy confirmation. Diagrams of the structure of both the complexes used for the second optimisation are shown below:

After this was done, a second optimisation was done on the complexes using the same calculation method (B3LYP), but using the more complex LANL2DZ basis set and pseudo-potential. This result in an improvement and more accurate optimisation. The additional words "opt=loose" were replaced with "int=ultrafine scf=conver=9", this was done due to the use of the better bases and pseudo-potential being used for the second optimisation and this requires a tight convergent, which is what this string does. Once this optimisation was complete, one final optimisation was performed. Although the LANL2DZ basis set and pseudo-potential is a lot more accurate than the LANL2MB basis set and pseudo-potential, it still has the flaw that it doesn't consider the d-orbitals, only valent s and p orbitals. As phosphorus does this its d-orbitals and is often hypervalent, the fact d-orbitals are not considers reduces the accuracy of the calculation. It is even mentioned in the output file that the phosphorus atoms maybe hydervalent. To improve the calculation, therefore, the input file can be modified so that d-orbitals are considered. This final optimisation was then run and the resulting structure are shown below and long with calculation data from the final optimisation:
File:Cis Opt3 mol.molFile:Trans Opt3 mol.mol
| Cis Complex | Trans Complex | |
|---|---|---|
| Calculation Type | FOPT | FOPT |
| Calculation Method | RB3LYP | RB3LYP |
| Basis Set | LANL2DZ | LANL2DZ |
| Energy (Before considering d orbitals) | -623.577 a.u. | -623.576 a.u. |
| Gradient(Before considering d orbitals) | 0.000003 a.u. | 0.00002 a.u. |
| Dipole Moment (Before considering d orbitals) | 1.31 Debye | 0.30 Debye |
| Energy (After considering d orbitals) | -623.693 a.u. | -623.694 a.u. |
| Gradient(After considering d orbitals) | 0.00005 a.u. | 0.000008 a.u. |
| Dipole Moment (After considering d orbitals) | 0.07 Debye | 0.22 Debye |
It can be seen from the table above that the Cis complex (-623.693 Hartrees or 1637506 KJ/mol) is slightly higher in energy than the Trans complex (-623.694 Hartrees or 1637509 KJ/mol). The reason for this most likely due to the steric clash between the two PCl3 in the cis complex, although it the energy difference between the two complexes is only 3 KJ/mol. These results here that the Trans complex is energetically more stable than the Cis complex thermodynamically is confirmed experimentally by Darensbourg2, who found that under thermodynamic conditions that cis-[Mo(PPh3)2(CO3)] readily isomerises to trans-[Mo(PPh3)2(CO3)] and in the calculations performed here it is assumed that -Cl grouped are similar to -Ph groups electronically. However, Bennett et al3 found that cis-[Mo(PPh3)2(CO3)] was more stable electronically in the gas phase and suggested that the reason that the trans-complex may seem more stable is due molecule-molecule interactions and environmental factors in solids. If it was wanted that the cis-complex of the type [Mo(PR3)2(CO3)] was the more stable and less reactive than the trans complex, then the R group should -OH. An -OH group would allow intra-molecular hydrogen bonding between the -P(OH)3 groups as they are next to each other in a cis-complex, where as intra-molecular H-bonding would not be possible this complex if the -P(OH)3 were trans as they would be too far away. It maybe suggests that H-bonding could be possible to the -CO groups, although distance and ordination is most likely still going to be an issue. The H-bonding would lower the energy of the complex, making the cis complex more stable. If it was wanted to make the trans-complex of the type [Mo(PR3)2(CO3)] a lot more stable than the cis complex, then make R a very large alkyl group. This would increase steric clashes between the large next to each other in the Cis complex, increasing it energy, but would make little difference to the trans-complex, as the large -PR3 are on the opposite sites of the molecule.
To insure that the optimisation reactions had been carried out successfully, some of the bond lengths and angle in the molecules were compared to the bond lengths and angles seen experimentally. This shown below:
| Calculated Cis | Calculated Trans | Experimentally4, 5 | |
|---|---|---|---|
| Mo - P length | 2.47Â | 2.42Â | 2.35Â |
| P - Cl length | 2.11Â | 2.12Â | 2.03Â |
| Mo - CO length | 2.02Â | 2.05Â | 2.06Â |
| C - O length | 1.17Â | 1.17Â | 1.14Â |
| Cl-P-Cl angle | 100.2O | 100.2O | 100.3O |
It can be seen that the calculated structural feature match what is normally see experimentally, suggesting that the optimisation was carried out successfully and the energies given above are valid.
Next, the frequency calculations were carried out on the cis and trans complex in order to calculated their vibrational spectrums and compare them to each other as well as to experimental data. This was done using the same basic sets and calculation method as before. Shown below are the two calculated spectrums:


From the spectrums above, it can be seen that the vibrational modes of the Cis and Trans isomers are very different, with the cis complex having a lot more vibrations on its spectrum. Below is given assignment to the most intense frequencies:
| Cis Frequency (cm-1) | Motion | Trans Frequency (cm-1) | Motion |
|---|---|---|---|
| 443 | Phosphorus groups asymmetric stretch | 435 | Phosphorus groups asymmetric stretch |
| 466 | Phosphorus groups symmetric Bending | 453 | Phosphorus groups symmetric Bending |
| 483 | Phosphorus groups symmetric stretching | 455 | Phosphorus groups symmetric Bending |
| 567, 586, 600 | CO bending | 577, 578 | CO bending |
| 1939, 1941, 1952, 2019 | CO stretching | 1939, 1940 | CO stretching |
The most important vibrations are the C0 stretches. As these are intense vibrations and often appear in a section on a IR spectrum where there are no other characteristic absorbance. Therefore, so Cis and Trans isomers with carbonyl groups in it, it is often possible to identify which of the isomers has be synthesised by taking an IR spectrum. The number of carbonyl peaks in the spectrusm of these complexes can be predicted by group theory as the point group of the two complexes are known (Cis complex = C2, Trans Complex = Cs). It is considered what would happen if the symmetry elememts that are assoicated with the point groups was applied to the CO stretches, whether it remains the same or becomes inverted. By doing this, a character for the vibration can be found. It is know that for a vibration to be IR active, the character related to the vibration most also relate to the either Tx, Ty or Tz. The results of doing this is shown below, as well as the experimental values for the CO stretches. It was consider that the vibrations could be defined as either symmetric (both CO stretching at the same time) or anti-symmetric (one CO stretches, whilst the other CO contracts).
| Frequency (cm-1) | Symmetry Character | Active accourding to Group Theory? | Experimental Frequency2 (cm-1) |
|---|---|---|---|
| 1938.1 | B | Active | 1886.7 |
| 1941.5 | B | Active | 1898.5 |
| 1952.4 | A | Active | 1913.7 |
| 2019.1 | A | Active | 2012.4 |
| Frequency (cm-1) | Symmetry Character | Active accourding to Group Theory? | Experimental Frequency2 (cm-1) |
|---|---|---|---|
| 1939.2 | A' | Active | 1885.4 |
| 1939.9 | A' | Active | Not seen |
| 1966.9 | A' | Active | Not seen |
| 2025.5 | A' | Active | Not seen |
From tables above using group theory, it is predicted that there should be 4 IR active vibrations for both the Cis and Trans Complex. For the Cis complex, experimentally there is 4 IR active CO stretches that can be seen in IR spectrums and from the data above, it can be observed that the calculated frquencies are very close to the experimental frequencies. However, for the Trans complex, group theory predicts 4 IR active CO streches, but only 1 is seen experimentally. The reasons for this is due to the symmetry of the molecule and degeracy. The frequencies at 1966.9 and 2025.5cm-1 are caused by symmetric stretching, which causes little change in the diople and hence is not seen experimentally and is only just seen as a weak intesity in the calculated vibrational spectrum. As the frequencies of the other vibrations are very close and nearly degrenarate, it will be very difficult to see two peaks in the IR spectrum for these CO streches and one is normally only seen. Note that neither of these considerations affects the Cis complex, due to the symmetry of the Cis complex. It can also be seen that the experimental and calculated frequency are very close in value for both complexes, showing that these calculation are very accurate and useful in predicting characteristics of molecules. Moreover, the calculated CO stretches for both complexes are similar in frequency, with the Trans complex having slightly higher frequecies, suggesting that the CO group are attached slightly stronger to the Mo centre, although the differnces in calculated frequencies between the molecules are very low
It was noted when studing the vibrational spectrums calculated for both the Cis and Trans complexes that there were some very low frequency (and hence energy) vibrations for both molecules. These are shown below, along which the frequency they occured at:




As these "rock" and "wag" motions are very low in energy, it would be expected that at room temperature the complexes would have enough energy to move in these motions. This maybe a important fact, as it means the molecules symmetry may be broken if these motions are slow and this would have an effect on both comlexes electronic properties, their UV spectrum and their extension coefficient.
Calculations
Below is give the DOI to the data in D-space
http://hdl.handle.net/10042/to-4008 - 3rd Optimisation for the Cis Complex
http://hdl.handle.net/10042/to-4009 - 3rd Optimisation for the Trans Complex
http://hdl.handle.net/10042/to-4010 - Frequency Calculation for the Cis Complex
http://hdl.handle.net/10042/to-4011 - Frequency Calculation for the Trans Complex
Investigating Noble Gas Compounds
The stability of Xenon Fluoride Compounds
The noble gases were thought to not form compounds, due to the fact that they already have a full octet of electrons and all their atomic orbitals are full, until 1962 and the discovery of XePtF6. After this discovery, a lot of research was done into noble gas compounds and a large number of different compounds were synthesised. One of the first set of noble gas compounds to be synthesised were Xenon Fluorides. Xeon, being the second largest noble gas after radon, has large and diffuse orbitals where the electrons are further away from the nucleus (compared to other noble gases) making it more reactive compared to the other noble gases. However, it is still a noble gases with all it atomic orbitals full and so is still very inert and only react with the most reactive of element. Fluorine is the most reactive element in the periodic table and if Xenon and Fluorine gas are mixed in light, Xeon Fluorides are formed. The type of Xenon Fluoride formed depends on the temperature the reaction is carried out at and the pressure of Fluorine gas used. There is a major difficulty in performing this reaction in the fact that Fluorine reacts with Silicon Dioxide, the main compound found in glass. This means in order to synthesis Xenon Fluoride special reaction vessels have to be used. Also, Xenon Fluorides are very unstable and readily act as Lewis bases to give fluoride ions. Therefore, experimentally to study Xenon Fluorides (and any Noble gas compound) is very difficult. However, it is possible to used computer calculations in order to study and predict the properties of these compounds and other Noble gas compounds.
It is commonly accepted that there are 3 possible Xenon Fluorides; XeF2, XeF4 and XeF6. First, it wanted to be known which of these 3 compounds is the most stable. In order to find this out, the 3 compounds have to have their structure optimised to the lowest energy confirmation and the energy of this confirmation has to be solved. However, there is a potential problem with doing this calculation as if this calculation was performed as was done above using the B3LYP basics set a number of factors would be ignored that are important in these compound and not so important when considering the molecules studied above, such as columbic effects, electron correlation effects and induced dipole effects. Therefore a different calculation method has to be used, the MP2 method. MP2 stands for Moller-Plesset Perturbation Theory. This type of calculation takes into account interactions between electrons in a quantum system by starting using simple mathematical expressions to build up a more complex express for the system being calculated. The simple expression is "corrected" in order to make it more realistic to the system to be studied and the "corrections" can be found by approximation methods and this is what is calculated by the computer and Gaussian. To compare the accuracy of the MP2 and the B3LYP calculation method, all 3 of the Xenon Fluoride compounds were optimised to their lowest energy structure using both the MP2 and the B3LYP and then a frequency calculation was performed using both the MP2 and the B3LYP calculation method to give the vibrational spectrum of the 3 compounds. These were then compared to the vibrational spectrum seen experimentally (IR spectrum) in order to see how much more accurate the MP2 method is. For both tyres of calculations (MP2 and B3LYP) the basic set used was the 3-21G basic set, which as described above is not a very accurate basic set but the calculation done using this basic set takes little time. The results of this for the 3 Xenon Fluoride compounds are shown below:
| Calculation Method | B3LYP | MP2 |
|---|---|---|
| XeF2 | -7401.89 a.u. | -7398.58 a.u. |
| XeF4 | -7600.14 a.u.* | -7596.49 a.u.* |
| XeF6 | -7798.67 a.u. | -7794.25 a.u. |
| Calculation Method | B3LYP | MP2 |
|---|---|---|
| XeF2 | 0.00003 a.u. | 0.000006 a.u. |
| XeF4 | 0.018 a.u.* | 0.036 a.u.* |
| XeF6 | 0.000003 a.u. | 0.000004 a.u. |
It can be seen that for the energy surface gradient for XeF4 (shown by * as are the energy values relating to the gradient values) are very high and suggest that the optimisation calculations did not complete correctly and this is the case, as the results of the optimisation did show an coordinate system error. This was further confirmed by the presents of negative frequency vibrations when the frequency calculations were performed on these optimisations of XeF4. Attempts were made to fix this error, such as altering the input file and basic set used, but the error unfortunately could not be removed. Therefore, the frequency calculation for XeF4 cannot be used to compare to the experimental vibrational spectrum for the same molecule. Below is shown the frequency calculation data and spectrums calculated for Xe2 and Xe4:
| Calculation Method | B3LYP | MP2 | Experimental6, 7 |
|---|---|---|---|
| XeF2 | 192.31, 470 | 176, 484 | 213, 516 |
| XeF6 | 117.04, 567 | 209.05, 558.53 | 200(approx), 563 |


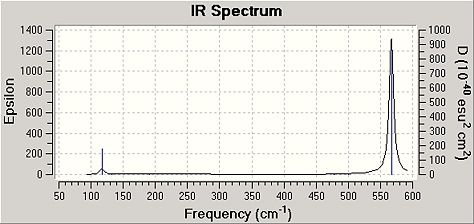

The 200cm-1 experimental frequency for XeF6 is only a prediction due to the difficulty in the experimental technique observing frequencies below 500cm-1 for XeF6. Also, the vibrations shown above have other modes which are related to the vibration shown by symmetry. From the results above, it can be seen that both types of calculations do give good approximations for the frequencies of the observable vibrations (other frequencies were calculated, but these have zero intensity, so are not given here as they cannot be compared to experimental data), although the MP2 method is slightly more accurate approximation for the XeF6 system. This is assumed to be due to the fact it considers electronic effect that are not considered by the B3LYP method, as explained above. However, it can be seen that the B3LYP calculation method can be used to quickly gain fast approximations.
Considering the total energy of the 3 molecules, it can also been seen that both calculation methods give similar values for the total energy and that when only considering the total energy of the system the stability of the products goes from XeF6 being the most stable (-20463803.38), then XeF4 (-19944584.5) and XeF2 (-19424971.79 KJ/mol) being the most unstable. (It should be noted that the energy value for XeF4 is being used here and as mentioned above, this value is a very unreliable result. But as the optimisation calculation failed on the XeF4, it is known that the energy value used for XeF4 is a upper limit; the energy of the molecule can only be lower than the value given. Therefore it is known that XeF4 cannot be higher in energy than XeF4. The energy value found for XeF4 will be used in this report, but it is known that it is extremely unreliable and has a large error associated with it) However, just comparing the energies of the 3 molecules is not going to accurate as each of the molecules have a different number of atoms a thus have a different number of bonds that contribute to the total energy of the molecule. This means that it is possible for one of the compounds could be lower in total energy but has lots of weak bonds which can be broke, making the molecule unstable overall. One way to get round this problem is to consider the energy change when forming the 3 Xenon Fluorides. This is shown below:
Xe + F2 ---> XeF2 Energy Change = +236.3 KJ/mol
Xe + 2F2 ---> XeF4 Energy Change = +210 KJ/mol
Xe + 3F2 ---> XeF6 Energy Change = +1444 KJ/mol
Note. Energy data found using the total energy calculated by the MP2 method. Total energy for Xe = -7200 a.u. and total energy for F2 = -197.9 a.u. The first thing to observe from above is the fact that going from reactant to products (Xenon Fluorides) the energy increases. This suggests that these reactions are not thermodynamically possible. This finding maybe due to the inaccuracies caused by using a simple basic set. Calculations were tried with more complex basic sets (such as the 6-31G basic set), but these calculation failed with an error that the basic set cannot be used with large atoms, such as Xenon. As it is experimentally known that these reactions are thermodynamically possible, it demonstrates a possible weakness of these calculations in the fact they cannot handle large atoms. However, if that fact is not considered, it can be seen from above that XeF4 is the most stable product (smallest increase in energy going from reactants to products). Note, although there is a large error on the energy of XeF4, the energy value is a maximum value, as explained above. Therefore, the energy increase from reactants to XeF4 can only decrease, so it will always be the most stable when considering energy changes. It would be predicted that the reason for XeF4 being the most stable is due to it having to steric issues and the strength of the Xe-F bonds. Comparing the Xe-F bond strength for XeF2 and XeF6, it can be seen from the frequency spectrum that the Xe-F bond is stronger in XeF6 than in Xe2 due to the fact that the Xe-F bond stretch occurs at a higher frequency in XeF6 (~550cm-1) compared to XeF2 (500-1). It would be predicted that the Xe-F strength in XeF4 would be in between that of XeF2 and Xe6, although this cannot be shown by a frequency calculation on XeF4 as the optimisation calculation failed on XeF4. Note, stronger bonds results in more stabilisation energy. If this was the case, XeF6 would be the most stable. However, XeF6 has steric issues, mainly due to the fact that it has sterically active lone pair on the Xe. This increases its energy and makes more unstable, resulting in XeF4 being the most stable. Shown below is Jmol of the 3 molecules, as well as HOMO and LUMO for each of them:
File:XF2 Opt.molFile:XF4 Opt.molFile:XF6 Opt.mol


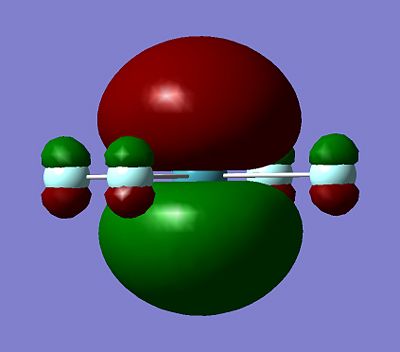
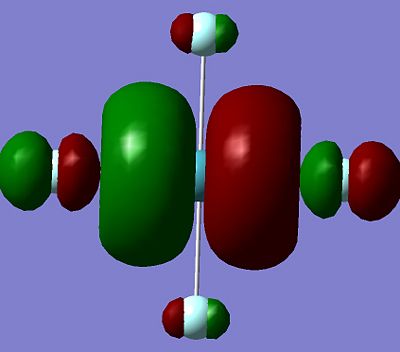

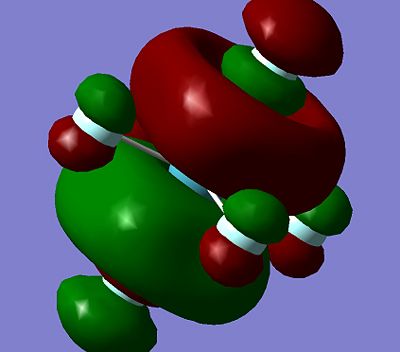
It can be seen all the HOMO and LUMO for this set of the molecules are very similar, with the p orbitals on the flouuine atoms seen in both the HOMO and LUMO for all the molecules. The orbital on the central Xenon atom for all the HOMO and LUMO shown above is predicted to also to be a p orbital, except for the XeF6 HOMO for which the characteristic two orbital lobles can not be seen on the Xenon atom. It is hard to predict which orbital is being seened by the Xenon to mix with the fluorine orbitals on the XeF6, but it is expected to be a d-orbital. The fact that the Xenon in XeF6 is using a different orbital in it's HOMO compared to the other Xenon Fluoride compound may explain why it has stronger bonds to the fluorine than the other two Xenon Fluoride compounds, although more calculation would have to be done to in order to make this a more solid prediction instead of a suggestion.
Note. The Calculated bond length of Xe - F was found to be 2.14Â in XeF2 (MP2 Calculation) which is close to the experimental value of 1.92Â6 considering the approximations made by using a very basic basic state and gives an idea of the accuracy of the calculations. It should also be noted that the point groups of the molecules for the optimasations were as follows: XeF2 = D*H, XeF4 = D4H, XeF6 = Oh
Calculation
Below is given the DOI to the data in D-Space:
http://hdl.handle.net/10042/to-4012 - XeF2 Opt B3LYP http://hdl.handle.net/10042/to-4019 - XeF4 Opt B3LYP
http://hdl.handle.net/10042/to-4014 - XeF2 Freq B3LYP http://hdl.handle.net/10042/to-4020 - XeF4 Opt MP2
http://hdl.handle.net/10042/to-4015 - XeF2 MO B3LYP http://hdl.handle.net/10042/to-4021 - XeF4 MO B3LYP
http://hdl.handle.net/10042/to-4016 - XeF2 Opt MP2 http://hdl.handle.net/10042/to-4022 - XeF4 Opt, PhD supervisor method and sets
http://hdl.handle.net/10042/to-4016 - XeF2 Freq MP2
http://hdl.handle.net/10042/to-4023 - XeF6 Opt B3LYP http://hdl.handle.net/10042/to-4030 - XeF2 Opt MP2 6-31G set - Failed
http://hdl.handle.net/10042/to-4027 - XeF6 Freq B3LYP http://hdl.handle.net/10042/to-4031 - F2 Opt MP2
http://hdl.handle.net/10042/to-4029 - XeF6 MO B3LYP http://hdl.handle.net/10042/to-4032 - Xe Opt MP2
http://hdl.handle.net/10042/to-4026 - XeF6 Opt MP2
http://hdl.handle.net/10042/to-4028 - XeF6 Freq MP2
Xenon Fluorides as Lewis Acids
Xenon Fluorides can act as strong Lewis bases as they are all unstable compounds by donating fluoride ions to other molecules a shown below: XeFn ---> XeFn-1+ + F- This reaction is another reason why Xenon Fluoride are difficult to handle and why it is preferable to investigate them using computational techniques. Tramsek and Zemva6 state that with respect to the reaction above and the acting as a Lewis base, XeF6 is the strongest, then XeF2, followed by XeF4. Note, this order of the Xenon Fluorides acting as Lewis bases agrees with the findings given above that for the stability of the Xenon Fluorides, as it would be expected that the least stable XeF6 would most readily break down following the reaction given above and hence would be the strongest Lewis base, where as the most stable XeF4 would not so readily break down, so won't be as strong Lewis base. This can be investigated computationally using the same calculation as performed to compare the stability of the Xenon Fluorides, comparing the energies of the reactants and products of the reaction of Xenon Fluorides acting as Lewis bases. Therefore, the products of this reaction (XeF+, XeF3+, XeF5+ and F-) were all optimised using the B3LYP calculation method (the MP2 Calculation method was tried but resulted in errors due to the fact that the calculations did not converge) and 3-21G basic set and then the energy change of the reactions was calculated. This is shown below:
| Compound | Energy |
|---|---|
| XeF+ | -7302.30 a.u. |
| XeF3+ | -7500.54 a.u. |
| XeF5+ | 7699.07 a.u. |
| F- | -99.15 a.u. |
Then using the data given above for the B3LYP calculation of the energies of the Xenon Fluorides:
XeF2 ---> XeF+ + F- Energy change = 1155.22 KJ/mol
XeF4 ---> XeF3+ + F+ Energy change = 1181.48 KJ/mol
XeF6 ---> XeF5+ + F+ Energy change = 1181.48 KJ/mol
It can be seen again that the calculations suggest that these reaction are not thermodynamically possible, as it results in products higher in energy than the reactant. It possible that this is due to a less complex calculation being used (B3LYP) which ignore some electronic effects. This may also explain why the data calculated does not match what is seen experimentally in the fact that the calculations suggest that XeF6 is the weakest Lewis base, not the strongest. Also, it may be due to the fact that these calculations don't take into account kinetic effects and it maybe kinetic effects which makes XeF6 the experimentally strongest Lewis base, not thermodynamic effects, although as mentioned above, the experimental finding for the Lewis base strengths do match the data for the thermodynamically stability of the Xenon Fluorides.
Calculations
Below is given the DOI of the data in D-Space
http://hdl.handle.net/10042/to-4032 - XeF Opt B3LYP
http://hdl.handle.net/10042/to-4034 - XeF3 Opt B3LYP
http://hdl.handle.net/10042/to-4035 - XeF5 Opt B3LYP
http://hdl.handle.net/10042/to-4036 - F Opt B3LYP
http://hdl.handle.net/10042/to-4037 - XeF5 Opt MP2 - Failed
Structure of XeF6
As explained above for when considering the stability of Xenon Fluorides, XeF6 has a sterically active lone pair of electrons that makes it an unstable molecule. As it has a sterically active lone pair, it has been suggested that its lowest energy confirmation may not be octahedral (point group Oh), which was the confirmation used for Xe6 for calculation of its stability and total energy. Crawford et al8 suggested that the point groups C2V and C3V maybe a more stable confirmation for XeF6 than the point group Oh. This idea was investigated by build Xe6 with the point groups C2V and C3V and finding the lowest energy confirmation when constraint to these point groups and comparing the energy with the total energy for when XeF6 is constraint to the point group Oh. The structures were first optimised using the B3LYP method and it was found that all three of the different point groups resulted in an energy of -7798.67 a.u., suggesting that all the structures resulting from the different point groups had very similar energy. It was noted that all the optimised structures were very close to the octahedral structure, resulting from the Oh point group. Therefore the optimisations were run again using the MP2 calculation method. However, the calculations failed to fully converge. Therefore the calculations failed to confirm whether confirmations resulting from the point groups C2V and C3V are lower in energy for XeF6 than the confirmation resulting from the Oh point group. Its suggested that the MP2 calculation would have to be left for a longer time and allowed more steps to converge. Crawford et al, who did do these calculations, did find that the confirmations resulting from C2V and C3V are lower in energy for XeF6 than the confirmation resulting from the Oh point group, due to less steric clashes involving the lone pair of electrons. Note, all the calculations done here were done using the 3-21G basic set. Shown below is XeF6 with the C2V and C3V point groups before optimisation.
File:XeF6 C2V mol.molFile:XeF6 C3V mol.mol
Calculations
Below is the DOI for the data in D-Space
http://hdl.handle.net/10042/to-4038 - XeF6 C2V Opt B3LYP
http://hdl.handle.net/10042/to-4039 - XeF6 C3V Opt B3LYP
http://hdl.handle.net/10042/to-4040 - XeF6 C3V Opt MP2 - Failed
Possible XeF8?
Frlec et al9 suggested the possibility of a XeF8 compound, where two of the fluorine atoms on XeF6 are replaced with fluorine molecules. Here, it is investigated to see whether it could exist theoretical and what the structure of this molecule would be.
The Molecule was first built with 8 Fluorines bonded to the central Xenon atom in a anticubic fashion with the point group D4h, and then this structure was optimised using the B3LYP calculation method and the 3-21G basic set (MP2 calculation was tried, but failed to converge). The result of this is shown below in the Jmol file. The energy of the molecule was found to be -7997.1 a.u. and the gradient of the energy surface was 0.00004 a.u.
It can be seen that in the calculated structure, it can be seen that 6 of the fluorine atoms are bonded to the central xenon atom and one fluorine atom bonded though its F-F bond. However, it is possible that the fluorine atom may not be bonded/interacting with the xenon atom. To check that this is a XeF8, not a XeF6 plus a Fluorine molecule, 2 things can be investigated, the molecular orbitals and the frequency of the F-F vibration in the fluorine molecule. First, the molecular orbitals were calculated for XeF8 and the HOMO and LUMO are shown below:
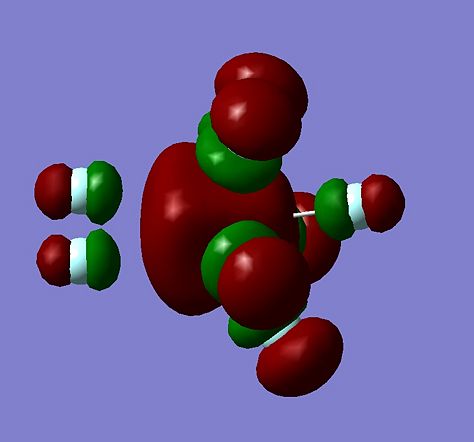

It can clearly be seen for the HOMO, that there is interaction between the orbital on the Xenon and the anti-bonding orbital on the fluorine molecule, suggestion some bonding action is occur, suggesting this is a XeF8 molecule.
Further evidence can be found when looking at the vibrational spectrum for XeF8, which is shown below. This was calculated using the same basic set and calculation method used for the optimisation (3-21G and B3LYP):
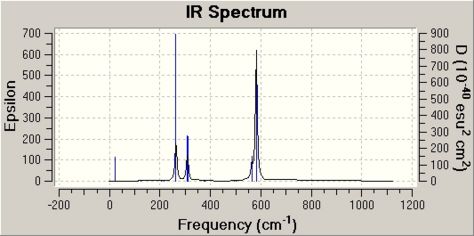
Although it cannot be seen on the spectrum, there is a very weak frequency that occurs at 1098.93cm-1 that is the F-F bond stretch in the Fluorine molecule. The frequency of this bond stretch was also calculated for free fluorine using the same methods and was found to occur at 1116.26cm-1. The fact that the frequency of this bond has gone down in XeF8 means that the F-F bond in the fluorine molecule is weaker in XeF8 (lower frequency bond stretch, weaker bond) and suggests that there is interaction between the Xe atom and the fluorine molecule. From the HOMO, it would be predicted this is most likely to be the donation of the lone pair on the Xe into the anti-bonding orbital on the fluorine molecule. Therefore, the calculations here does suggest that XeF8 is theoretically possible, but unlike Frlek et al suggestion the calculations here suggests that 6 of the fluorines are bonded to the xenon atom and one fluorine molecule complexes to the xenon, not four fluorine atoms and 2 fluorine molecules.
Calculations
Below is given the DOI for the data in D-Space
http://hdl.handle.net/10042/to-4041 - XeF8 Opt B3LYP
http://hdl.handle.net/10042/to-4042 - XeF8 Freq B3LYP
http://hdl.handle.net/10042/to-4043 - XeF8 MO B3LYP
http://hdl.handle.net/10042/to-4046 - XeF8 Opt MP2 - Failed
Xenon Chloride and Radon Compounds
It was experimented if Xenon Chloride compounds were possible. These compounds were built and then had there structure optimised using the MP2 method and 3-21G basic set. XeCl2,XeCl4 and XeCl6 were all tried as direct analogues of the Xenon Fluoride compounds. The results of the optimisation calculations showed that these molecules are not thermodynamically stable and the atoms dissociated, suggesting that Xenon Chlorides are not feasible molecules. The structures optimised structures for XeCl2 and XeCl6 are shown below showing how they dissociated:
It was then thought that maybe there could theoretical be Radon Chlorides. Radon is the next Noble gas after Xenon and is also the largest. Being the largest, it has very diffuse orbitals and thus is the most reactive of the Noble gases (As you go down the Noble gas group, the atomic orbitals get more diffuse, making the atoms more reactive, so the order of reactivity is from least to most, He, Ne, Ar, Kr, Xe and Rn. However, as all of these have a full outer orbital, they are all very unreactive). Radon is also radioactive, so studying Radon using calculation would be a lot more preferable compared to experimentally. However, when calculations were tried with Radon, the calculations failed due to the size of radon and the basic sets could not be used. A number of basic sets were tried but the error message back from the calculation was that the basic set could not be used above Xenon. Therefore, it can be seen that a weakness of these calculations is they cannot exploit the weakness of experimental method, in the fact that heavier elements are harder to handle experimentally due to their toxicity, especially the Actinides.
Calculations
Below is given the DOI for the Data in D-Space
http://hdl.handle.net/10042/to-4049 - XeCl2 Opt MP2
http://hdl.handle.net/10042/to-4050 - XeCl4 Opt MP2
http://hdl.handle.net/10042/to-4051 - XeCl6 Opt MP2
http://hdl.handle.net/10042/to-4052 - Rn Opt MP2 - Failed due to basic set.
Helium Compounds
As suggested above, Helium is the most unreactive atom in the perodic table. There are no known neutral Helium compounds. However, Koch et al10 have done a number of computational studies on possible theoretical Helium compounds. They suggest that instead of reacting with highly polarised atoms, such as Li or F, He would more preferable to form compound with atoms such as itself, carbons and boron. They suggested that instead of trying bond He to electronegative atoms/groups, that it should be tried to bond it in acceptor atoms and groups; they suggest that is a atom has "sigma holes" (low lying empty sigma orbitals) while the p orbital are occupied, it is poosible that a strong bond will form to the He atom in cations.
This is investigated the possibility of He compounds, first two theoretical compounds that have alreay been suggested to be stable, He22+ (first proposed by Pauling in 1933) and HeC2+, to show here that He compounds can be stable. The two molecules were optimised to their lowest energy confirmation using the B3LYP method (as small atoms are being used) and a 3-21G basic set. Structures of these two molecules are shown below in Jmol files:
It can be seen that He22+ is calculated to be thermodynamically unstable and dissociates, even though it is seen experimentally in charge stripping mass spectrometry. The reason it is calculated to be unstable is possible due to the fact that experimentally He22+ is found to be metastabe. This means that the moleculeis thermodynamical unstable toward dissociation, but there is a large energy barrier which stops it from doing so. It is most probable that in the optimisation calculation this energy barrier is not considered, resulting in it being found to be an unstable molecule. A more complex calaculation is needed to show that it is actually thermodynamically stable. However, it can be seen that HeC2+ is found by the optimisation calculation to be a stable He compound.
Koch et al investigate a number of theoretical He compound by using stability calculation, using calculation methods such as MP2, to see if they are thermodynamical stable. The paper studies both cations and neutral He compound. Here, two theroretical He compounds will be investigated to see if they are stable by opitisation calculations; HeCF2 and HeC(CF3)2. These molecules are chosen as they are neutral compounds that are similar to the stable HeC2+ compound and the electron withdrawing molecules will maximise the positive charge on the carbon atom, as it can be see that there is a positive charge on the carbon in HeC2+. The optimisation calculations were carried out using the B3LYP method and 3-21G basic set as above. The optimised structure of the molecules are shown below:
File:HeCF2.molFile:HeC(CF3)2.mol
It can be sen that both molecule dissociate and thus are not thermodynamically stable. This is not surpising, but the what is shown above is more that they molecule are unstable. The calculations show how easy theoretical molecules using computational studies. There calculations took less than a hour, where as a lot more resources and man power, as well as cost, would be required to test if these theoritical molecules are stable "in the lab". This demostrates how useful computational studies and allows experimental work to be more focused to experiments and sythesis that are calculated to "work" and thus computational studies are valuable tool to the modern chemist, allowing to save time and resouces.
Note: For information, Koch et al found from their studies/calculations, that HeBN and HeBeO are best candidates for a stable neural He compound, with the latter being stable with all levels of calculation they tested it with.
Calculations
Shown below are the DOI for the data in D-Space:
http://hdl.handle.net/10042/to-4089 - He2 Opt B3LYP
http://hdl.handle.net/10042/to-4090 - HeC Opt B3LYP
http://hdl.handle.net/10042/to-4091 - HeCF2 Opt B3LYP
http://hdl.handle.net/10042/to-4091 - HeC(CF3)2 Opt B3LYP
References
1. Kawaguchi, J. Chem. Phys, 1992, Vol 96, No. 5, p3411
2. Darensbourge, Inorg Chem, 1979, Vol 18, No. 1, p14
3. Bennett et al, J. Chem Crystallography, 2004, Vol 34, No. 6, p353
4. Alyea and Song, Inorg Chem, 1995, Vol 34, p3864
5. CRC Handbook of Chemistry and Physics, 90th ed, 2009
6. Tramsek and Zemva, Acta Chem Solv, 2006, Vol 53, p105
7. Kim et al, Inorg Chem, 1968, Vol 7, No. 3, p616
8. Crawford et al, J. Chem Phys, 1995, Vol 102, No. 8, p3307
9. Frlec et al, J. Inorg Chem, 1970, Vol 32, p2521
10. Koch et al, J. Am Chem Soc, 1987, Vol 109, p5917