Rep:Mod:TomTaylorMod1
The Use of Molecular Mechanics and Semi-empirical Molecular Orbital Methods for Structural and Spectroscopic evaluations
The formation and Hydrogenation of Cyclopentadiene Dimers
It is known that two molecules of cyclopentadiene can react together in a cycloaddition pericyclic reaction (π4s + πs electrons) to form a dimer. This is shown below in Reaction Scheme 1:
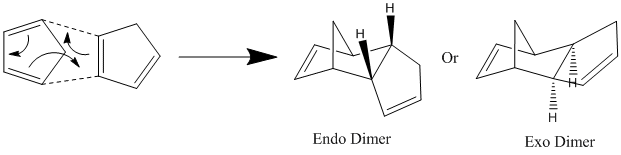
It can be seen that this reaction the product can either be of the exo form or the endo form. Experimentally it is seen that the endo product predominates. Knowing this fact, it is possible to use a computer simulation to find out whether this reaction is under thermodynamic control or kinetic control. This is done by considering the energy of the two possible products.
After building a model of both the possible products, as shown above in the reaction scheme, it is possible to find the energy of both the products by using a MM2 force field. This is a computer program that considers all the force in a molecule, such as stretching, bending and torsion of the chemical bonds, as well as considering the effects Van der Waals forces and Hydrogen bonding and works out what is the lowest energy confirmation for the molecule and the energy of this confirmation, balancing all the factors explained above. The results of this is shown below:
| Energies | Exo | Endo |
|---|---|---|
| Stretch | 1.29 | 1.27 |
| Bend | 20.59 | 20.85 |
| Stretch - Bend | -0.84 | -0.84 |
| Torsion | 7.67 | 9.50 |
| Non-1,4 Van der Waals | -1.44 | -1.51 |
| 1,4 Van der Waals | 4.23 | 4.29 |
| Dipole-Dipole | 0.38 | 0.44 |
| Total Energy | 31.88 | 34.01 |
It can be seen that the energy of the exo product (31.88 Kcal/mol or 133.39KJ/mol) was lower than the energy of endo product (34.01 Kcal/mol or 142.30 KJ/mol). As it is known that the high energy endo product is the major product of this reaction, the MM2 force field calculation suggests that this reaction is not under thermodynamic control (otherwise the lower energy exo product would be the major product) and is instead under kinetic control. This finding means that the transition state leading to the endo product must be lower in energy then the transition state leading to the exo product. It also suggests that steroelectronic factor must also be taken into account to understand this reaction, something which the MM2 calculation cannot do, as it only considers classical physics. Considering the results give above by the MM2 force field calculation, it can be seen that the main difference in the energy between the endo and exo product comes from the higher torsion strain in the endo product. It can be seen in the pictures above that the endo product molecule is far more bent than the exo product and this bending in the endo product results in it have more torsion strain and possible steric clashes, with the hydrogen atoms on the underside of the ring.
From the endo product, it is considered what would happen if the molecule was hydrogenated. It is know that initially only one of the two carbon double bonds is hydrogenated first and that more forcing conditions are need to hydrogenate the second double bond. This gives rice to two possible products as shown in Reaction Scheme 2 below:
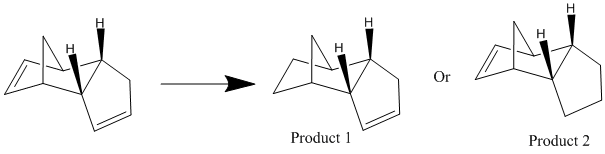
Using the MM2 force field calculation again, it is possible to find out which of the two possible products has a lower conformation energy. As it is assumed that this reaction is under thermodynamic control, it is known that which of the two possible products has the lower conformation energy will be the major product of the reaction. The results of the calculation is shown below:
| Energies | Product 1 | Product 2 |
|---|---|---|
| Stretch | 1.08 | 1.23 |
| Bend | 14.54 | 18.92 |
| Stretch - Bend | -0.54 | -0.76 |
| Torsion | 12.51 | 12.17 |
| Non-1,4 Van der Waals | -1.06 | -1.52 |
| 1,4 Van der Waals | 4.51 | 5.75 |
| Dipole-Dipole | 0.14 | 0.16 |
| Total Energy | 31.17 | 35.94 |
It can be seen that the lower energy product of hydrogenating the endo dimer of cyclopentadiene is Product 1 (31.17 Kcal/mol or 130.42 KJ/mol), hence Product 1 would be the major product of this reaction and the higher energy Product 2 (35.94 Kcal/mol or 150.37 KJ/mol) is the minor product. When comparing the different energy values, it is seen that the main difference in energy between the two products is in the Bending energy (14.54 Kcal/mol or 60.84 KJ/mol for Product 1 and 18.92 Kcal/mol or 79.16 KJ/mol for Product 2). This suggests that the double bond in 6 membered ring is bent from its normal geometry and this cause Product 2 with the double bond still in the 6 memebered ring to be higher energy than Product 1. Normally it would be expected that the double bond in smaller ring would be higher energy, as the smaller the ring is the less flexible it is and any double bond in the ring more bent from its normal position (and hence making the double bond in a 5 membered ring higher in energy than the double bond in the 6 membered ring in the Cyclopentdiene dimer). However, because there is a bridge head in the 6 membered ring, the ring is less flexible and more rigid and causes the double bond in the 6 membered ring to be higher in energy. It also causes this double bond to be part of a 5 membered ring as well, with the bridge head. As this double bond, in the 6/5 membered ring is higher in energy, it is hydrogenated first, resulting in Product 1 being the major product of this reaction. When considering all the other different types of energies of Products 1 and 2, it can be seen that they are very similar to each other and the main contributions to the total energy for each of the products comes from the bend and the torsion energies, with the torsions energy contribution coming from the fact that the molecule is bent and this could result in steric clashes as explained above for the endo product.
Stereochemistry of Nucleophilic Addition to a Pyridinium Ring (NAD+ Analogues)
NAD+ is molecule located in Eukaryote cells and has an important role in the respiration, acting a proton carrier in the citric acid cycle and transports protons collected here to the Mitochondrion, so that there is proton steep gradient (concentration of proton) going from the inside of the Mitochondrion (high proton concentration) to the outside (low proton concentration). This allows protons to diffuse though the enzyme ATP synthase, from the inside of the Mitochondrion to the outside, which catalysis the product of ATP, the energy used by all life. The section of the molecule that allows NAD to transport protons reveribly is the pyridine ring, which has an group attached to the nitrogen, resulting in the nitrogen having a positive charge. This section of the report is concerned with molecules that have this same structure (pyridine ring with a positive charge on the nitrogen) as part of them and how computer modelling and calculations can be used to predict the stereochemistry of reactions on this group.
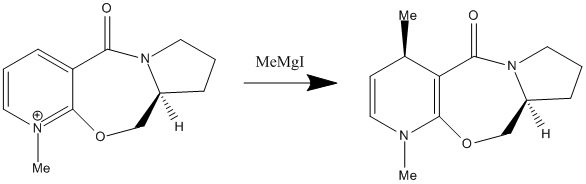
Considering Reaction Scheme 3 given below, it is known that it always results in the stereochemistry of the product as shown:
The reason for this can be explained by considering the lowest energy configuration of the reactant. By building a model of using a computer interface, a MMFF94 force field can be applied to the reactant in order to find the lowest energy of this molecule and the lowest energy configuration. Two possible lowest energy configurations are shown below:
File:Pyridinium ring 5b.molFile:Pyridinium ring 5a.mol
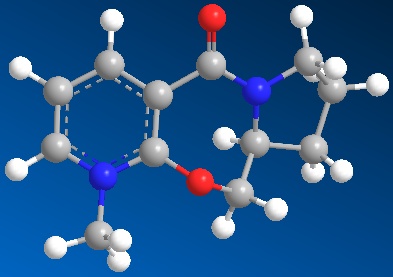

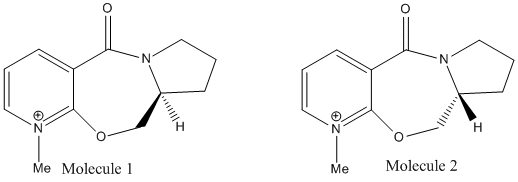
It can be seen that Molecule 1 has the same stereochemistry to the reactant in the nucleophilic addition reaction given above, where as Molecule 2 has different stereochemistry. This is shown below:
This small change in the stereochemistry has a large effect in stereochemistry of the product of this reaction. It can be seen in the Jmol files above, that when looking at the position of the carbonyl group, it can be seen in Molecule 1 (the reactant used in reaction scheme 3) it is pointing up slightly above the plane of the pyridine ring in the molecule (Angle between the carbonyl and pyridine ring = 37o). This is critical to understanding the stereochemistry of the product. It has been proposed that the mechanism of this nucleophilic addition follows the mechanism given below1:
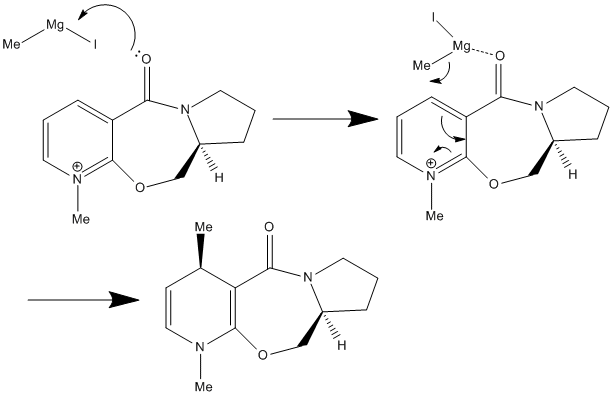
It can be seen that the in the first step of the mechanism that the Grignard reagent (MeMgI) coordinated to the carbonyl on the molecule before the nucleophilic addition occurs in the second step of the mechanism. Therefore, when performing the nucleophilic reaction above with the given stereochemistry, the carbonyl group is slightly above the plane of the pyridine ring, so when the Gridnard reagent coordinates to the carbonyl group, it is above the plane of the pyridine ring, and so delivers the Me group to the top face of the ring and this is what is seen in the product, with Me group on the top face of the ring. If this nucleophilic addition reaction was carried out with Molecule 2, it would be predicted that the Me would be delived to the bottom face of the structure and the product would have the opposite stereochemistry. This is due to the fact that the on this molecule the carbonyl group is slightly below the plane of the pyridine (Angle between the carbonyl and pyridine ring = -28o) and as the reaction follows the same mechanism, using the same argument given above, it can be seen that the Me will be delivered to the bottom face of the ring. It should be noted that the energy of Molecule 1 and Molecule 2 are very similar (59.13 Kcal/mol or 261.26 KJ/mol and 58.97 Kcal/mol or 260.55KJ/mol respectively) It should also be noted that the MMFF94 calculation could not be performed on the Gridnard reagent to find its lowest energy confirmation as these molecular mechanics calculations can only be performed on certain groups and molecules and not on molecules with metal atom in it, a weakness of this method. A further weakness was found when trying to find the lowest energy confirmation of the reactant. The calculations gave back confirmations that were very similar in confirmation to Molecule 1, but a lot higher in energy. It is assumed these molecules represent a local minimum in energy on the energy surface when balancing all the strain energy factors, but are obviously not representative of the lowest energy confirmation of Molecule 1. One of these is shown below as an example. It has an energy of 291.40 Kcal/mol or 1219.22 KJ/mol and the angle between the carbonyl and pyridine ring is 39o
A second nucleophilic addition reaction which the stereochemistry of the products can be explained by molecular mechanics is shown below in Reaction Scheme 4. Again it has a structure similar to that of NAD:

Again, the lowest energy confirmation of the reactant can be found by using a MMFF94 force field. This gives the confirmation shown below:

In this reactant (Molecule 3), the carbonyl is below the plane of the pyridine ring (Angle between the carbonyl and pyridine ring = -38o). However, it is know that the -NHPh group is delivered to the top face of the pyridine ring, so coordination of the nucleophile is not the explanation for the stereochemistry in the product, as seen in the first nucleophilic addition reaction or the -NHPh would be delivered and bonded to the bottom face of the pyridine ring. The reason for why this reaction processed with the stereochemistry shown is due to steric interaction between the carbonyl group and the large -Ph group on the nucleophile2. The carbonyl group blocks the bottom face of the pyridine from nucleophilie, as the nucleophilie for this reaction is large and only allows the -NHPh to attack the top face of the pyridine ring (opposite face to which the carbonyl group is sticking out on), resulting in the stereochemistry shown. Molecule 3 was drawn in a number of different ways on the computer interface, but the result of using the MMFF94 force field was always the same, resulting in the carbonyl sticking below the pyridine ring (the energy of this confirmation is 98.29 Kcal/mol or 411.25 KJ/mol). Although these molecular mechanics models can be used here to predict and explain the outcomes of reaction, the MM2 and MMFF94 force field have the weakness that they don't consider the electronic effects and the effects of orbitals and the wavefuctions of the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO); these methods only consider classical mechanics cause as bond bending and stretching energy. A way to improve these method would be to use a more quantum mechanical approach to include electronic and orbital effects. MOPAC/PM6 force field calculation is a semi-quantum mechanical calculation, that considers these interactions and can be used to find an approximation of the wavefunction for the HOMO and LUMO which then can be used to explain some reaction and the stereochemistry of some reaction. It is used later in this report to find an approximation of molecular orbitals of a molecule to understand its reactivity towards an electrophilie.
Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol
Taxol is an anti-cancer drug that was discovered by the National Cancer Institute. It is action is on the microtubule, which holds cells together, acting as a flexible scaffold in the cell, causing it to be rigid and non-flexible, which results in the cell being up able to divide by mitoses or carry out its normal function. It is also found to cause apoptosis (cell death) in cancer cells. It is found natural in the bark of a yew tree, but removing it from the tree causes the tree to die, so a suitable source of it had to be found and attempts were made to synthesis it.
One method of synthesising Taxol was proposed by Paquette and includes the following Cope-reaction as part of the synthesis:
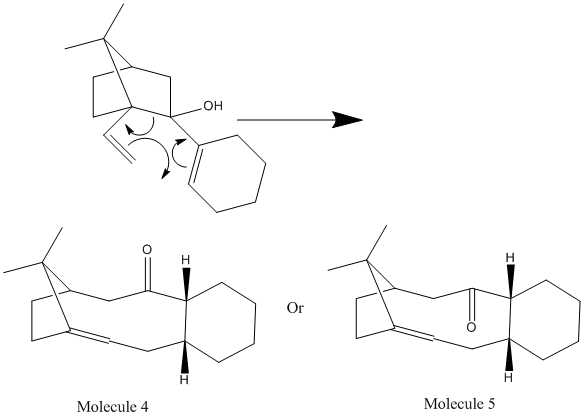
Molecule 3 and 4 are Atropisomers, isomers that are caused by restricted rotation around a single bond. In the case above, it can be seen that this restriction results in either the carbonyl either pointing up or pointing down. As it is known that this reaction results in the most stable product (product with the lowest energy), the MM2 and the MMFF94 force fields can be used to predict which isomer (Molecule 3 or 4) will be the major product. The results of the MM2 force field calculation is shown below:
| Energies | Molecule 4 | Molecule 4a | Molecule 5 | Molecule 6 |
|---|---|---|---|---|
| Stretch | 2.81 | 2.70 | 2.56 | 2.81 |
| Bend | 16.41 | 15.89 | 10.66 | 13.58 |
| Stretch - Bend | 0.45 | 0.40 | 0.32 | 0.65 |
| Torsion | 21.38 | 18.11 | 19.65 | 21.95 |
| Non-1,4 Van der Waals | -0.78 | -0.99 | -1.25 | -1.33 |
| 1,4 Van der Waals | 14.05 | 12.63 | 12.53 | 15.42 |
| Dipole-Dipole | 0.14 | 0.15 | -0.18 | 0.00 |
| Total Energy | 54.47 | 48.89 | 44.29 | 53.08 |
Its found that Molecule 5 is lower in energy than Molecule 4 (44.29 Kcal/mol or 185.31 KJ/mol and 54.47 Kcal/mol or 227.90 KJ/mol respectively) The main difference in the energies of these two isomers occur between the Bend energies, as well as some difference between the Torsion and 1,4 Van der Waals energies. The larger bending energy in Molecule 4 is most likely to be caused by the fact that the 6 membered ring in Molecule 4 is in a twist boat conformation which is higher in energy than the favoured, lower energy chair confirmation which is seen in Molecule 5. In order to try to manually lower the energy of Molecule 4, the 6 membered ring on Molecule 4 was changed to the chair confirmation, creating Molecular 4a. A MM2 force field was then applied in order to find the lowest energy confirmation of this molecule. It was found that the energy of Molecule 4a (48.88 Kcal/mol or 204.51 KJ/mol) was lower than the energy of Molecule 4, demonstrating a weakness of the molecular mechanics method in the fact that minimised energy can be incorrect sometimes due to the calculation getting "trapped" in local energy minima, which is seen in Molecule 4. This is further demonstrated by changing the positions of atoms in Molecule 5 in the 6 membered ring to form a twisted boat (forming Molecule 5a) and when this structure was minimised by the MM2 force field, it resulted in a confirmation that was higher in energy (53.21 Kcal/mol or 222.63 Kcal/mol) than the starting confirmation (Molecule 5). The atoms in the 9 membered ring were also changed in confirmation, (forming Molecule 5b) and again when the MM2 force field was applied, the resulting confirmation was significantly higher in energy than Molecule 5 (90.65 Kcal/mol or 379.28 Kcal/mol), hence experimentally, it would be expected that very few of Taxol intermediates would have the structures shown in Molecule 5b, although Molecular Mechanics does suggest this confirmation is possible. Returning to Molecule 4a, it was still seen that this molecule is higher in energy than Molecule 5, still suggesting that the most energetically favourable conformation (and hence major confirmation) is that with the carbonyl group pointing down, as well as having the 6 membered ring in the chair confrimation. The major difference in the energies between Molecule 4a and 5 is still between the two molecules Bend energy, suggesting that in Molecule 4a having the carbonyl group is sticking up put more bend strain in the bonds in the 9 membered ring, hence increasing the energy compared to the case where the carbonyl is sticking down (Molecule 5). I would assumed that the difference between the energies of Molecule 4a and 5 has little to do with the 6 membered ring, as in both Molecule 4a and 5 the 6 membered ring is in a chair confirmation. The structure of all the molecules mentioned here are shown below:
File:Taxol9.molFile:Taxol10.molFile:Taxol9a.molFile:Taxol10bFile:Taxol10a
The energies of the Molecules 4, 4a and 5 were compared also when using MMFF94 force field instead of the MM2. It was found that the energy of Molecule 4 was found to be 76.34 Kcal/mol or 319.41 KJ/mol, energy of Molecule 4a was found to be 70.54 Kcal/mol or 295.14 KJ/mol and the energy for Molecule 5 was found to be 60.56 Kcal/mol or 253.38 KJ/mol, showing that the MMFF94 force field agreed with the MM2 force field in the fact that Molecule 4 is the highest energy confirmation, the Molecule 4a and Molecule 5 has the lowest energy confirmation. However, as the two calculation methods use different methods to solve the energy of the two molecules, the values enegies found by the MM2 and MMFF94 force fields cannot be compared. It is known that the double bond in taxol intermediate is very difficult to hydrogenise and considered to be a "Hyperstable Alkene". This can be rationalised by applying the MM2 force field to the product of the hydrogenation of the double bond in the taxol intermediate to form Molecule 6 This done using Molecule 5 as the reactant that will be hydrogenised, as this is the lowest energy conformation of the taxol intermediate and so it would be expected that most of the intermediate molecule has this confirmation. It is found that Molecule 6 has a higher energy confirmation (53.08 Kcal/mol or 221.96 KJ/mol) than Molecule 5. It was noted that the structure of Molecule 6 has the 6 membered ring in a chair confirmation, the lowest energy confirmation, so the energy of the molecule cannot be lowered by changing its confirmation. This also suggests that the increase in the torsion, bend and 1,4 Van der Waals energies, which are the energies that increase the most from going from Molecule 5 to Molecule 6 is caused by the confirmation of the 9 member ring. This also suggested by the fact that the double bond being hydrogenised is in the 9 membered ring. The fact that the Molecule 6 is higher in energy than Molecule 5, suggests that the double bond in Molecule 5 will be very hard to hydrogenise as it results in a product that is higher in energy that the react and hence suggests that this reaction is thermodynamically unfavourable. Maier et al3,4 first coined the term "Hyperstable Alkenes" when investigating compound similar to those shown here and found that alkenes were more stable than alkanes when using a MM1 force field (Normally alkanes are more stable than alkenes, hence why alkenes are easily hydrogenised to alkanes). He suggested that this was due to the position of the double bond near a bridge head, which is what is seen here. He also found the Olefinic Strain energy by taking the total strain energy of the alkane from the total strain energy fo the alkene. If this is done here, the Olefinic Strain energy of going from Molecule 5 to Molecule 6 is found to be -8.79 Kcal/mol or -36.78 KJ/mol, which as the value is negative, shows that the double bond actually stables the molecule. If the calculation (using a MM2 force field) are repeated when hydrogenising Molecule 4a, when the double bond is pointing up, to give Molecule 7, it is found that the energy of Molecule 7 is 67.17 Kcal/mol or 281.03 KJ/mol (Note, this energy was found after manually insuring the 6 membered ring was in chair confirmation), showing the confirmation of Molecule 4a is also a "Hyperstable Alkene" The calculation were also performed using a MMFF94 force field giving a energy of 71.48 Kcal/mol or 299 KJ/mol for Molecule 6 and 100.90 Kcal/mol or 422.17 KJ/mol for Molecule 7. As both of these values are higher than their parent alkene molecule (Molecule 5 and Molecule 4a respectively), the MMFF94 force field calculation agrees with the MM2 force field calculation in the fact that Molecules 4a and 5 are "Hyperstable Alkenes". Structures of Molecules 6 and 7 are shown below:
File:Taxol10h.molFile:Taxol9h.mol
Regioselective Addition of Dichlorocarbene
Shown below is the structure of Molecule 8:
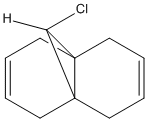
It can be seen from the diagram above that the molecule is asymmetric, due to the chlorine atom in the bridge head and that it could react with an electrophile on either of the two double bonds in the structure. In order to work out which of the two double bond the electrophile would react with two methods could be used. Either the energies of both the possible products can be found by using Molecular Mechanics as before or the molecular orbitals can be found and this will suggest which double bond the electophilie will attack. As seen before, the first method has the weakness that it ignores electronic effects, which often have a large effect. So, the molecular orbitals will be found for Molecule 8. To achieve this, the Molecular Mechanic method and calculations will not be enough, as this only considers classical physics, where as when considering molecular orbital electronic effects have to be taken to account, so a Quantum mechanical approach has to be taken. To this extent, a semi-classical method (semi-quantum method) will be used. First, the molecule was built in the computer interface and the lowest energy confirmation was found using a MM2 force field as before. Then a PM6 calculation was performed to calculate the molecular orbitals. Some of these are shown below:
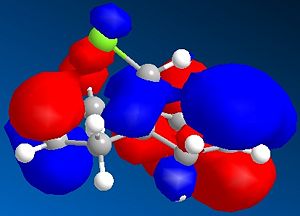
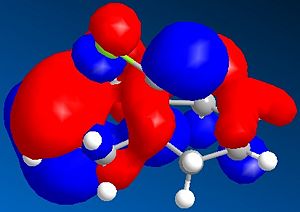
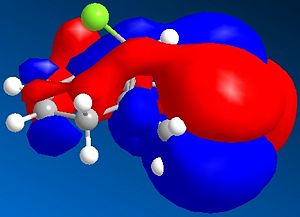
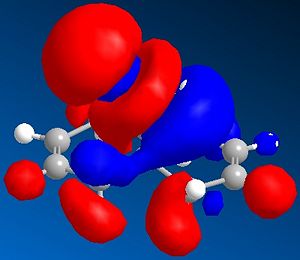
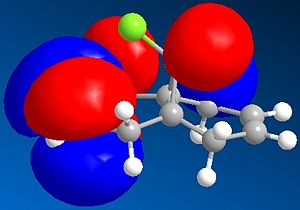
Considering the fact that an electrophilic addition reaction involving Molecule 8, such as the reaction between Molecule 8 and a peracid to form an epoxide, the electrophilie would attack the position of the electrons that is in the highest energy orbital (the HOMO), which are, hence, the most reactive and accessible for attack by the electrophile. From the diagrams above it can be seen that the wavefunction for the HOMO molecular orbital indicates that the double bond on the same side as chlorine atom is more likely to be attacked, as the wavefunctions showns that there is a greater possibility that the highest energy electrons will be located there. However, if Molecule 8 was attacked by a nucleophilie, it would be expected that the attack would occur on the opposite double; the double bond on the opposite side to the chlorine atom. This due to the fact that in the LUMO has a greater wavefunction on this double bond (the double bond opposite to the chlorine atom). Testing the finding of the fact that the double bond that would be attacked by a electrophile on Molecule 8 would be the one the same side as the chlorine atom, Molecular Mechanics can be performed, assuming that the electrophile a peracid and the product of this reaction would be one of the two epoxides shown below:
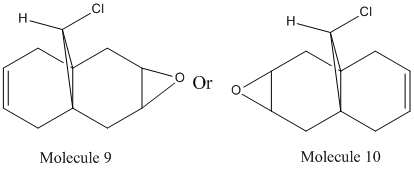
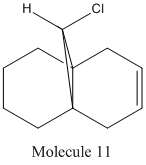
Molecule 9 is what is predicted and expected by the more complex semi-classical calculation, by the consideration of the HOMO wavefunction. When a MM2 force field was applied to both Molecules 9 and 10, in order to find the energy of their lowest energy confirmation, it was found that Molecule 9 had an energy of 127 Kcal/mol or 531.37 KJ/mol and Molecule 10 had an energy of 126.49 Kcal/mol or 529.23 KJ/mol (Note, this high energy is most likely due to the bent bond angle in the epoxide). It can be seen, therefore, if only a Molecular Mechanical approach was taken, it would be unable to tell which of Molecule 9 and Molecule 10 would be major product, were as considering the electronic effects by doing a semi-classical calculation, it can clear be seen that Molecule 9 would be the major product. Semi-classical calculations can also be used to calculate other properties of molecules, such as their IR spectrums. This can be done to assess how different bond have an overall effect on the IR spectrum of the molecule. In this example, still using Molecule 8, it was investigated the effect of the C-Cl bond has on the IR spectrum. The IR spectrum for Molecule 8 was calculated using Gassian, as was the IR spectrum of Molecule 11, the structure of which is shown below:
Shown below are the IR Spectrums for both Molecule 8 and 11:
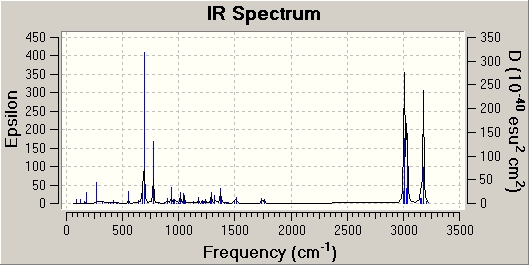
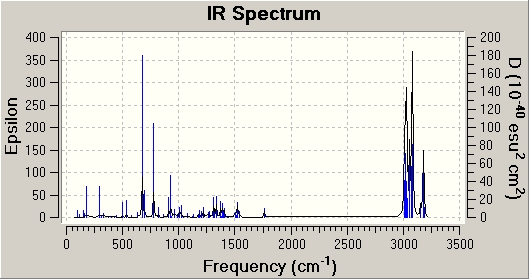
It was found that for Molecule 8, the carbon double bond stretches occurred at 1761cm-1 (double bond same side as Cl) and 1740cm-1 (double bond other side of Cl) and the strongest (most intense) carbon-chlorine stretch occurred at 773cm -1 (Peak just over 150 epsilon) Compared to this, it was found that for Molecule 11, the double bond stretch occurs at 1762-1 and the carbon-chlorine stretch occurs at 777cm-1 (Peak just over 200 epsilon). The first, it can be seen that the double bond stretches occurs at higher wavenumbers than the single bond stretch. This is exactly as expected, as double bonds require more energy to stretch than single bonds. Second, it can be seen that the intensity of the double bond peaks on both spectrums are very weak compared to that to the signal for the single bond stretch. This is due to fact that peak intensity is proportional to the change in the dipole moment when the bond stretches, the double stretches in both Molecule 8 and 11 doesn't result in much of a dipole change, due to the symmetry of both molecules, where as in both cases the carbon-chlorine stretch, with the chlorine being very electronegative, will result in a significant dipole change. The fact that peak intensity is proportional to change in dipole also explains why the carbon-chlorine stretch in Molecule 11 is more intense than it is in Molecule 8. The fact that in Molecule 11, the double bond on the opposite side to the chlorine has been removed, when the chlorine stretches towards the remaining double bond a greater dipole can occur than when that double bond is still there (double bond opposite side to the chlorine), as in Molecule 8. This is due to the fact that a double is more electron rich than a single bond, as act like a "counter balance" of electrons in Molecule 8 when the chlorine stretches away from it, decreasing the dipole, where as in Molecule 11, the is no "double bond counter balance", so a larger dipole is possible and results in a greater intensity peak for the carbon-chlorine stretch in Molecule 11. This idea is further backed up when comparing the HOMO of both Molecule 8 and 11. It can clearly be seen that in Molecule 11 HOMO, most the wave function density is on the chlorine side of the molecule, where a the HOMO for Molecule 8 is more evenly spread (although it is more dense on the chlorine side, as explained above). So when the chlorine does stretch in Molecule 11, a greater dipole occurs and an more intense signal in the IR for this stretch.
Finally, from going between the two IR spectrums, it can be seen that the carbon-chlorine and the chlorine side double bond stretch both occur at similar wavenumbers (energy) in both molecules, which is expected, as the structure around both these groups is essential the same in both molecule. Also, it should be noted that the double bond stretch on the opposite side to the chlorine in Molecule 8 occurs at lower wavenumbers (energy) than the chlorine side double bond stretch. This is most likely to be due to the fact there is a greater electron density in the chlorine side double bond, make it a stronger bond, than the double bond on the opposite side to the chlorine. This can be seen from the HOMO for Molecule 8. Stronger bonds require more energy to stretch, hence why the chlorine double bond occurs at higher wavenumbers.
Investigating and predicting the regio-chemistry of the formation of 5-aryl-2oxazolidiones from CO2 and aziridines using an amino acid catalyst
From the sections above have shown how computer calculation and techniques, namely Molecular Mechanics and Semi-Classical calculation can be used in organic chemistry, predicting the lowest energy conformation for a molecule and the energy of this, the wavefunction for molecules and chemical spectrum. In this section of the report, it will be shown how these techniques can be used to predict the 13C NMR of molecules and how this can be used to idnetify the products of a reaction where the product is one of two isomers. Jiang et al5 reported the reaction below, where one of two isomers is given as the product:
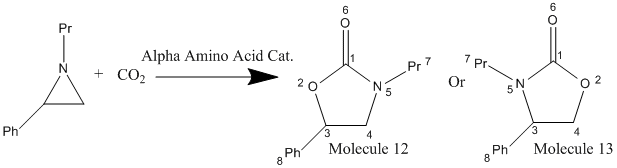
(Note Ph = Phenyl group, Py = Propyl group)
The paper included 13C NMR data for the product. Using a Semi-Classical calculation, it is possible to predict the 13C NMR spectrum for both the possible products (Molecules 12 and 13) and then compare them to the experimentally found 13C NMR spectrum and by doing so, it should be possible to identify the structure of the product of this reaction. The predicted 13C NMR chemcial shifts for both Molecule 12 and 13 are shown below with the experimentally found 13C NMR chemical shifts6,7 (The data shown is the chemical shift in ppm and the atom numbers relate to the atom numbers shown in reaction scheme 5, where 8 is the atoms on the phenyl ring and 7a is the carbon bonded to the nitrogen on the propyl group and 7c is the terminal carbon on the propyl group. For both the computer calculations and experimental the solvent used was CCl3 and the reference is TMS. The bases set used was 6-31G.):
| Atom Number | Molecule 12 | Molecule 13 | Experimentally Found |
|---|---|---|---|
| 1 | 150.55 | 151.92 | 157.9 |
| 3 | 71.93 | 60.96 | 74.2 |
| 4 | 53.71 | 70.27 | 52 |
| 7a | 46.01 | 44.15 | 45.7 |
| 7b | 23.41 | 20.02 | 20.5 |
| 7c | 12.7 | 12.65 | 11 |
| 8 (ipso) | 139.18 | 134.35 | 138.8 |
| 8 (ortho) | 119.95/121 | 122.73/125.53 | 125.4 |
| 8 (meta) | 124.67/125.23 | 124.92/125.9 | 128.6 |
| 8 (para) | 123.8 | 125.15 | 128.7 |
The difference between the two sets predicted 13C NMR chemical shifts and the experimentally found 13C NMR chemical shifts were found and these difference swere compared, as seen below in the graph below:
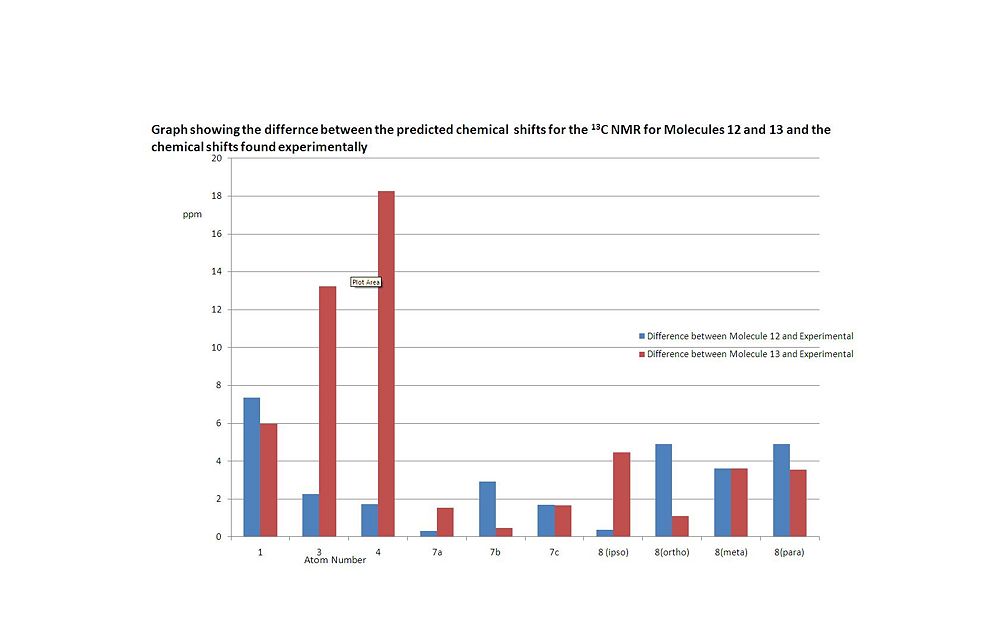
Note, only the magnitudes of the differences are considered here, not the sign.
It can be observed that both predicted sets of chemical shifts (for the two possible products; Molecules 12 and 13) are very close to the experimentally seen chemical shifts for all the carbon atoms and the differences betweens the predicted chemical shifts for Molecule 12 and what is seem experimentally and the differences betweens the predicted chemical shifts for Molecule 13 and what is seem experimentally for a certain carbon atom are very similar magnitude except for carbons 3 and 4 (For example, for carbon 1, the difference between experimental and predict Molecule 12 chemical shift is 7.5ppm and the difference between experimental and predict Molecule 13 chemical shift is 6ppm. It can be seen that these two differences are very similar in magnitude). For carbons 3 and 4, it can be seen that there is very large difference in the chemical shift values between given for Molecule 13 compared to the chemical shift given for the product experimentally, where as the chemical shifts for carbon 3 and 4 given by Molecule 12 are in agreement with the chemical shifts seen experimentally, suggesting that the product of Reaction Scheme 5 is Molecule 12. It should be noted that the paper doesn't assigned any of the chemical shift for the 13C NMR and it could be argued that the chemical shifts for carbons 3 and 4 have been assigned the wrong way round (ie. 52ppm for carbon 3 and 74.2 ppm for carbon 4, not the other way round as shown in table 4), but if this was done not only would be large differences between the chemical shift for carbon 3 and 4 between Molecule 12 and the experimental product, but there would still be a significant difference between the chemical shift value for carbon 3 between Molecule 13 and the experimental product (over 7ppm). This strongly suggests that Molecule 13 is not formed as the product. Jiang et al also found that experimentally that the major product of the reaction was Molecule 12, for reasons explained later in this report. All the other experimental chemical shifts can easily be assigned by comparing the value found experimentally with the chemical shifts for Molecule 12. The only signals which are difficult to assign as the phenyl hydrogens, due to the fact that they all have similar chemical shifts.
Although the semi-classical method can be seen to be able to help assign experimental NMR in this case, there are weaknesses to this method. For example, it is known that the chemical shifts given by these calculations carry a 2ppm error. For 13C NMR, where the chemical shifts are quite large, this has little effect, but is extremely significant for 1H NMR, where maximum chemical shifts are normally about 10ppm, so this method can not be used reliable to study 1H NMR. However, it is possible to use computer models to predict J-coupling between protons, using a program called Janocchion. Experimentally, many of the 1H NMR signals were multiplets, so didn't have a J-coupling value. Below is shown a diagram of the protons that did have a J-coupling value and comparing these values to what is predicted the J-coupling values for Molecule 12 and 13:
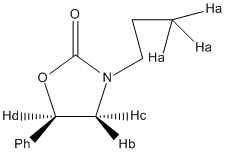
| Proton | Molecule 12 | Molecule 13 | Experimentally Found |
|---|---|---|---|
| a | 3 or 13.9 | 3.3 or 13.9 | 7.2 |
| b | 6.1 | 6.4 | 8 |
| c | 8.9 | 9 | 8.8 |
| d | 7.5 | 7.7 | 8 |
A number of observations can be made be when comparing the J-coupling values. First it can be seen that the J-coupling values predicted for Molecules 12 and 13 using Janocchion are very close to the experimentally seen values, using the accuracy of the computer calculations. However, this also means that the use of the J-coupling values to distinguish between the two isomers would not work and comparing the two predicted sets of J-coupling to what is seen experimentally would show which of the two isomers would be formed for this reaction. The reason for this is more to do with the reaction and the fact that the protons for which there is J-coupling information are in very similar environments in both isomers, resulting in similar J-coupling values. The final observation to notice is the fact that for protons in environment "a" give two different J-coupling values when predicted by Janocchion, where experimentally only one value for the J-coupling value. The reason for this is the fact that the computer calculation doesn't take into account the fact that bonds can rotate. Therefore in the calculation, when finding the J-coupling values for the different protons in this environment where the bond the protons are attached to can rotate, different J-coupling values are given, as J-coupling values have a dependence on the angle between the coupling protons. Experimentally, the bond rotates, resulting in an "average" environments, which is why the experimentally found J-coupling value for these protons is approximantly half way between the two values predicted by the calculations for both Molecule 12 and 13 for these protons.
It was also possible to predict the IR spectrums for both Molecule 12 and 13, using the same method as before, with the aim of confirming the fact that the major product of this reaction is Molecule 12, by comparing the IR spectrums to the experimentally found IR spectrum. Unfortuntely, no experimental IR data was given by Jiang et al or could be found else. But the predicted IR spectrums for both Molecule 12 and 13 are shown below:
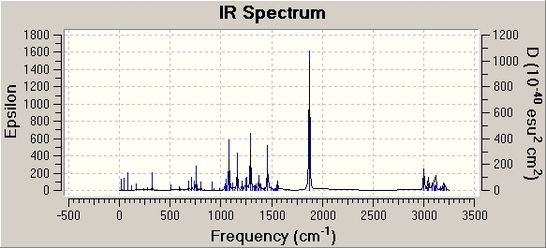

It can be seen that these two IR spectrums are very similar and comparing them to a experimental IR spectrum would not be very useful in determining which of the two possible isomers have been formed in reaction scheme 5. However, in both the calculated IR spectrums for Molecule 12 and 13, a very strong peak can be seen at around 1700cm-1; a characteristic peak for a C=O stretch and it can be seen clearly that there is a carbonyl group in both molecules.
From above it can be seen the use of computer calculation to predict spectrums and chemical properties in order to determine which of two possible isomers are formed in a reaction, with relation to reaction scheme 5. Now, it will be investigated if Molecular Mechanic and Semi-Classical calculations can predict correctly which of the two possible isomers is formed in reaction scheme 5, knowing it should find the structure of Molecule 12 should predominate.
First the minimum energy confirmation for Molecules 12 and 13 are found and the energies of these conformations. This was done using the MM2 force field). It is found that the minimum energy conformation for Molecule 12 has an energy of 14.52 Kcal/mol or 60.75 KJ/mol and the minimum energy conformation for Molecule 13 has an energy of 12.18 Kcal/mol or 50.96 Kcal/mol. This suggests that if this reaction (reaction scheme 5) was under theromdynamic control, Molecule 13 found be the major isomer. As it is know that Molecule 12 is the major product, this suggests that the reaction is not under thermodynamic control and other factor have an effect and this is seen to be the case. Below is shown the structures for the lowest conformations of Molecule 12 and 13:
File:2a Project 2a.molFile:Project 3a.mol
The mechanism suggested by Jiang et al for reaction scheme 5 is shown below:
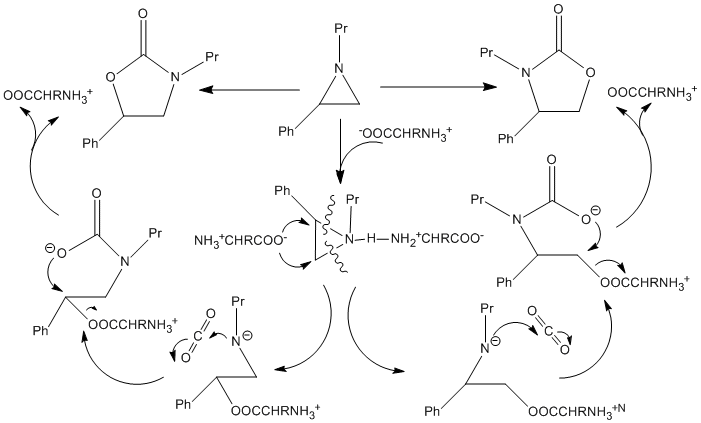
It can be seen that the step in the mechanism that determines which of the two possible isomers (Molecules 12 and 13) are formed is determined at step where the amino acid acts as a nucleophile and attacks the aziridine ring, either at the carbon with the phenyl group attached or the carbon without the phenyl group attached. As the electron from the amino acid enters the LUMO on the aziridine, it possible to calculate the LUMO on the aziridine ring using semi-classcial calculations on a computer and see whether this calculation can rationalise the fact the major product of this reaction is formed by attack of the amino acid on the carbon with the phenyl group attached in the aziridine ring. Below is shown the LUMO for the aziridine ring:
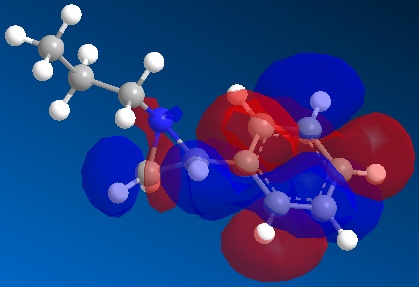
It can be seen that most of the LUMO wavefuction is concentrated on the phenyl ring, suggesting that nucleophilic attack should occur on the phenyl ring. As shown in reaction scheme 5, attack on the phenyl is not seen. This shows that both considering the molecular orbitals and the energy of the lower energy confirmation for Molecules 12 and 13 doesn't rationalise why Molecule 12 is the major product of reaction scheme 5. Jiang et al suggests that the reason that the amino acid attacks the carbon with the phenyl attached on the aziridine ring is for two reasons; first attacking the 3 membered ring results in the ring breaking and as a 3 membered ring is very strained, this is energetically very favourable. Second reason is the fact that when the amino acid attacks either carbon on the aziridine ring, a slight positive charge will build up on the carbon atom. As a more substitute carbon atom will be able to stabilise this slight charge better (resulting in lower energy transition state), it can be seen that attack will occur at the carbon with the phenyl group attached to it, as it is the most substituded of the two carbons, resulting in Molecule 12 being the major product. The first of these two reasons for the position of the seen attack (attack on the 3 membered ring, not the 6 membered ring) can be seen in the fact that the energy of the lowest energy confirmation found by the MM2 force field was very high (121.33 Kcal/mol or 507.64 KJ/mol) compared to that of Molecule 12 and 13, showing that the MM2 force does suggest that it is thermodynamically favourable to break this 3 membered ring. The second reason why attack occurs at the carbon with the phenyl attached cannot be explained by Molecular mechanics or Semi-Classical calculations, as these calculation are unreliable on transitions states, which have to be considered here to understand why attack at the most substituted carbon is favourable. In conclusion, the use of Molecular Mechanics and Semi-Classical calculation can be used to predict some characteristic of molecules, such as lowest energy confirmation, IR spectrums and NMR spectrums, allowing the ability to predict the products of some reactions and determine the product of reaction where one of two possible isomers are formed. But, these calculations don't work for all reactions and molecules and the calculations can get "stuck" in local energy minima on the energy surface instead of finding the actual energy minima and ignores some important effects, such as electronic effects and cannot be used on transition state. Therefore, computer calculation like the ones performed here are a valuable tool in organic chemistry but cannot replace experiments due to the fact the calculation don't consider everything and should be used alongside experiments to help predict rather than replace experiments where the calculations are expected to give exact results.
References
1) A.G Schultz et al, J.Org. Chem. 1986, 51, 838
2) S. Leleu et al, Asymmetry Tet, 2004, 15, 3919
3) P. Camps et al, Tetrahedron, 1997, Vol 55, No 28, 9727
4) W. F. Maier et al, J. Am. Chem. Soc., 1981, 103, 1891
5) H. Jiang et al, Tetra. Let., 2010, 51, 928
6) http://hdl.handle.net/10042/to-3728
7) http://hdl.handle.net/10042/to-3729
Note the last two is data calculated for the predicted 13C NMR for Molecules 12 and 13