Rep:Mod:This is not a test page.

Module 3: The Cope Rearrangement

The cope rearrangement is a [3,3]-sigmatropic electrocycle where the product is the reactant, 1,5-hexadiene.

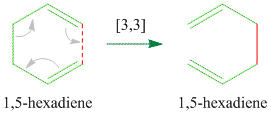
Optimising The reactants and products

Conformers of 1,5-hexadiene and their relative energies

Conformer	Point Group	Energy/Hartrees	Relative Energy / kcal/mol
	C2	-231.6926024	0.04
	C2	-231.6915302	0.71
	Ci	-231.692535	0.08

Differences between the HF/3-21G and the B3LYP/6-31g(d) levels of theory

	HF321G	B3LYP/6-31G(d)	Literature
C=C Bond Length/Å	1.316	1.334	Val3
C-C Bond Length/Å	1.553	1.548	3
C-H Bond Length/Å	1.077	1.098	4
Energy/a.u.	-231.6925	-234.6117	N/A

Thermochemistry

Using a frequency calculation, one can extract useful thermodynamic properties from the molecule. The table below lists out various energies for the Anti2 conformer using the B3LYP/6-31G* method.

Thermochemistry of anti2 conformer

	B3LYP/6-31G(d) 298.15K
Sum of electronic and zero-point Energies	-234.4692
Sum of electronic and thermal Energies	-234.4619
Sum of electronic and thermal Enthalpies	-234.4609
Sum of electronic and thermal Free Energies	-234.5008

Optimising the'Chair' and 'Boat' transition structures

The Chair transition state

The chair transition state was optimised using the TS(Berny) method. Optimising a transition state structure is more difficult than optimising to a minimum as information of the reaction coordinate needs to be included. This can be done in two ways. The first is making an educated guess at the transition state structure and optimising from there, the second is to set the distance between the immediate atoms involved with bond formation/dissociation and freezing them. The rest of the structure can then be optimised to a minimum before a transition state calculation can be run. This second way makes it easier to find a transition state as the error of finding the wrong energy maxima is reduced.

Using the first method, the molecules where arranged so that they lay in a chair fashion roughly 2.2Å apart. The calculation shows the vibration found form this method to be -817.97cm^-1.

Using the second method of freezing specific coordinates, the vibration was also found to be -817.76cm^-1 with a bond length of the transition state C--C of 2.0207Å compared to 2.0203Å for the former method. In conclusion, it is shown that both methods yield the same results.

The Boat transition state

To optimise the boat TS, we will define both the product and the reactant. Gaussian will then interpolate between these two structures to find the mid-point. The conformer used is the Anti2.

The method of optimisation used is QST2. Careful labelling is applied to both reactant and product to allow the calculations to be exact. The structure has to be modified a little however so that the right energy maximum is found. Some angles are changed so that 1,5-hexadiene looks like the in the images shown below.

Reactant	Product

Intrinsic Reaction Coordinates (IRC)

The reaction coordinate of the transition from product to reactant can be calculated alongside a graphical representation. The IRC of the boat transition state was calculated using 50 steps.

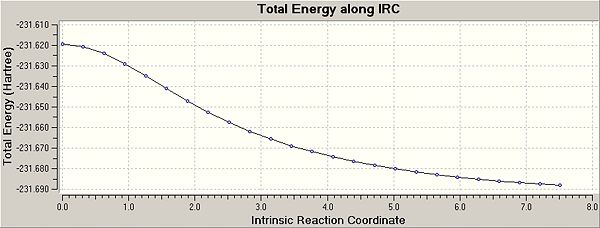
As the energy doesn't reach a minimum, the final structure calculated is not the most accurate representation of the product. There are two ways in which we can find the minimum. The first is quick and can be achieved by running an optimisation to a minimum of the final IRC structure and the second is calculating the force constant of the system at every point of the IRC calculation. The latter is more CPU intensive but both methods were tried to compare them. Usually, the problem with the first method is that the structure could be optimised to the wrong minima.

Implementing the first method afforded an energy level of using RHF/3-21G. The second method gave an IRC curve with a well-defined minimum as shown below:

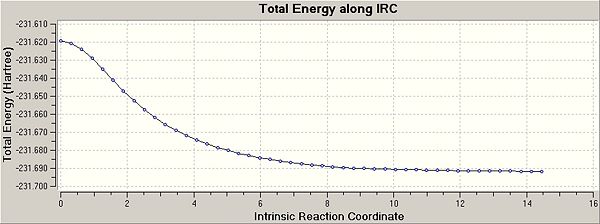
with an energy of using the same method and basis set as before. The energies are similar enough to give the correct result with confidence but by calculating a force constant at every step gives a more descriptive readout.

Optimising the final structures

The final step in the analysis is the optimisation of both chair and boat structures using the B3LYP/6-31G* method. The gives us an energy of -234.557a.u. whereas the gives an energy level of -234.543a.u. post-optimisation.

As can be seen with comparison to the 3-21G levels shown in the previous sections, the geometrical structures are the same, but given the higher level of theory, the 6-31G level of theory will give results closer to experimental values.

References and SCAN files

SCAN files for the calculations:
http://hdl.handle.net/10042/to-4847
http://hdl.handle.net/10042/to-4849
http://hdl.handle.net/10042/to-4848
http://hdl.handle.net/10042/to-4850
http://hdl.handle.net/10042/to-4852