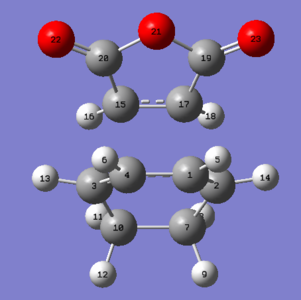
Rep:Mod:ThirdyearPSRWtransitionstructuresexp

Introduction

This computational study will utilise Guassview 5.0 to model potential energy surfaces (PES) for two pericylic reaction types. Firstly the Cope [3,3]- sigmatropic rearrangement of 1,5-hexadiene where chair and boat transition state structures and activation energies will be anaylsed. Secondly the [4+2]π Diels-Alder cycloaddition of ethylene and s-cis-1,2-butadiene followed by regioselectivity analysis with reference to the [4+2]π Diels-Alder cycloaddition of cyclohexa-1,3-diene and maleic anhydride by modelling both exo and endo transition state structures. Thermal Diels-Alder reactions are highly dependent on orbital symmetry following on from the Woodward-Hoffmann rules and therefore dienophile and diene π-system overlap will be crucial to reactivity. Specific molecular orbitals (MO's) will be shown to enhance many of the arguments put forward.

The simulations carried out rely on transition state theory, an approximation that assumes several things, the most important of which is that molecular systems that have crossed the transition state (TS) geometry in the direction of the products cannot turn around and reform reactant. This transition state geometry corresponds to a maximum potential energy on the reaction coordinate, a saddle-point, and is therefore a transient species with a lifetime so short only the newest attosecond probes can monitor them. As a result the only practical way to isolate these species for the reactions mentioned is to use computational methods. The theory also allows for reaction PES's to be determined as it assumes nuclear and electronic motions to be de-coupled. This is because nuclei mass far exceeds electronic mass and response times are far longer. This is equivilent to the Born-Oppenhiemer approximation in QM and allows for nuclei positions to be determined along reaction pathways.

This report will use three different levels of theory and approximations when calculating TS structures; Hartee-Fock/3-21G, Density Functional Theory(DFT)-B3LYP/6-31G(d) and semi-empirical/AM1 strategies. The first two theories are ab-initio and utilise different basis sets when computing molecular orbitals and have their roots in quantum mechanics. The AM1 level of theory only relates to a basis set to save computational time and is therefore semi-empirical but attempts to rectify errors associated with this simplification by carrying out a process of parametization against a database. Calculations carried out in this report will allow for the determination of the balance between the level of accuracy required vs. computational cost.

Furthermore two different methods will be used to locate transition state structures, the first of which uses an input guess structure and then optimizes this via the Berny TS method, or the frozen coordinate method, where specific bonds at the bond making/breaking sites of the guess will be fixed and the entire system will be relaxed around them before these sites themselves are optimized. The second, QST2, utilises atomically matched reactant and product species inputs and carries out a linear interpolation to locate the transition state on the PES between them. Note this method is only accurate for intramolecular reactions like the Cope rearrangement analysed. The latter method is empirical as it does not specifically consider quantum mechanics in its calculations.

Nf710 (talk) 09:43, 11 March 2016 (UTC) Very Nice intro

Cope Rearrangement Tutorial of 1,5-hexadiene

Prelude

Before using computational methods it is important to have solid understanding of the chemistry underpinning a particular reaction. The Cope rearrangement of 1,5-hexadiene is classified as a [3,3]-sigmatropic rearrangement pericyclic reaction. The reaction proceeds via a concerted 6-membered cyclic transition state and must obey the strict orbital symmetry rules laid down by Woodward and Hoffmann in 1965 for the conservation of orbital symmetry of which helps predict activation energies for these class of reactions. This report models the thermal reaction of which are allowed as the total number suprafacial and antarafacial components (4q + 2)_s + (4r)_a = 3, is odd.

Fig.1 The Cope Rearrangement of 1,5-hexadiene.

The concerted mechanism for the Cope rearrangement is widely agreed upon and therefore proceeds via an uncharged 6-membered cyclic transition state, of which can be via either chair or boat conformation, both are not only concerted but also synchronous. Both of these transition states can be considered energetically and structurally equivalent to a diradical and bears 10-15% more diradical character than the reactant species . However this will only proceed when the system PES is perturbed allowing such a species to become favourable. This report models the Cope rearrangement through a homo-aromatic transition state of which is seen in the transition states isolated. It has been found by CASSCF calculations that the boat TS has considerably higher entropy than that of the chair TS , but is largely unfavoured enthralpically and is overall higher in energy

In this report both the Hartee-Fock and DFT levels of theory are used to compute both the mentioned chair and boat transition state transient species for the Cope Rearrangement as well as for the initial reactant and product species associated with them by the reaction PES. The aim of this will be to locate and quantify these pericyclic reaction pathways activation energy and compare these to literature values. Further to this, specific conformations of 1,5-hexadiene will also be produced and optimized in Gaussview with the aim of determining the local energy minimum conformer.

Nf710 (talk) 09:44, 11 March 2016 (UTC) Great understanding of the mechanisms and well backed up with literature

Hartee-Fock and DFT

Before locating transition state species for the Cope rearrangement a discussion of the levels of theory used to compute them is required. The HF method has its roots in quantum-mechanics and in the MO solutions of the Schrodinger equation. The solutions are determined using slater determinant matrixes of N independent electronic wavefunctions, which become de-coupled, as the independent particle approximation is assumed, and all electronic-electronic interactions are an average property of the system, known as the mean-field. Each energy eigenfunction is assumed to be describable by a single Slater determinant of which are commonly used to describe the wavefunction of a multi-fermionic systems and satisfy the Pauli-exclusion/anti-symmetry requirements and as such the HF method outputs antisymmetric Hartree solutions of the Schrodinger equation. The main source of error in the HF method lies in the mean-field approximation - electrons of opposite spin may occupy the same spatial orbital in time arising from an entanglement between these electrons in the electronic structure of a quantum system. This is known as electron-correlation but this is totally neglected, however it does take into account exchange energies for electrons of parallel spin. Because of this Coulombic repulsion terms used in calculations are not accurate.

On the other hand the DFT [6-31G(d)] does take into account electron-correlation as determined in the first Henberg–Kohn theorem where the electron density of a many electron system is defined in 3 spatial coordinates and this electron density is used instead of MO wavefunctions. DFT therefore takes into account for an effective potential, namely an external potential and the effects of the Coulomb interactions between the electrons i.e. the exchange and correlation interactions within what is known as the Kohn–Sham framework. As stated before HF does takes into account exchange interactions i.e. between electrons of parallel spin. In addition polarization is incorporated into DFT calculations because of the (d) term after G (Gaussian), which stands for a polarization function is inputted in DFT calculations. The drawback of DFT is in its calculation of the exchange-energy as approximations such as the local-density approximation used are not exact and the total functional of this potential term remains unknown and this is hard to improve upon, meaning it is not able to converge towards an exact solution. This method does however incur a larger amount of CPU time for its calculations.

In terms of the B3LYP notation, B3 stands for Becke's three parameter exchange function and LYP stands for the Lee, Yang and Parr correlation functional. These functionals are what allows for DFT to take into electron correlation and relate electron density with energy, consequently improving upon the HF model. Despite being more computationally expensive, vastly more accurate data is obtained. Note than hybrid models such as the semi-empirical B3LYP scheme take into account aspects of both levels of theory. Such a case incorporates the exact exchange energy term determined by HF theory making the overall calculation more accurate.

In contrast the HF method can be improved simply by changing the MO basis set input. In this report the 3-21g (HF) and subsequently the 6-31(g)(DFT) basis sets are used, which better represents the core orbitals. The former is used for computational efficiency and is classified as a contracted basis-set. To reduce computation time less core-like, valence orbitals are focused on during calculations and does not take into account any polarization as no polarization functions are inputted. This is a good basis-set to choose for computing non-polar atomic systems such as hydrocarbons, where there is little polarization and where core orbitals contribute little to the reactivity observed. The latter basis set on the other hand takes into account more core-like orbitals which does make the computed system more accurate/realistic, but at the expense of more computation.

Optimization of specific 1,5- hexadiene conformations

In this section a global energy minimum conformation for 1,5-hexadiene will be located using HF levels of theory and a 3-21G basis set. Previous studies have shown that this molecule possesses ten energetically distinct conformers due to free rotation about its central carbon-carbon bond resulting in different torsional angles. Previous work carried out has determined that the gauche conformer is the lowest in energy. This report seeks to determine and qualify this result computationally and the anti-1/2 and gauche-3 conformers will be focused on.

To start trivalent and tetrahedral carbon center fragments are joined in Gaussview to produce an initial molecule bearing the correct bonding in 1,5-hexadiene. Then the central c-c bond torsion angle is rotated to 180° in order to produce a relative anti orientation of the terminal alkenyl groups. This process was repeated, except that a torsional angle of 60° was chosen to produce a gauche orientation of the terminal alkenyl groups. Both systems were then cleaned and symmetrized to ensure that the initial structures were near their respective local energy conformer minima and to ensure correct point groups were assigned.

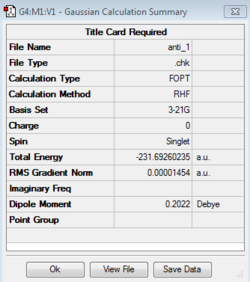
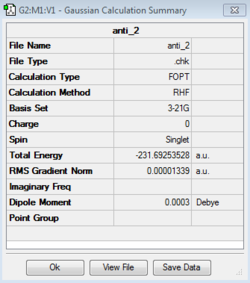
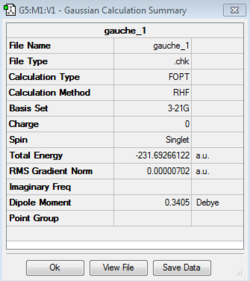
Separate calculations using the initial anti linkage molecule produced both the anti-2 and anti-1 conformers, the former possessing the C1 point group and the latter the Ci point group. These structures were scrutinized against the lab script appendix and were in agreement both in terms of their absolute and relative energies. It is seen that the anti-1 conformer was very slightly lower in energy with relative energies of 0.037 and 0.079 with respect to the gauche-3 conformer. The gauche-3 conformer was then produced and optimized resulting in a structure that quantitatively possessed a lower energy, -231.69266122 Hartrees and the C1 point group, as seen in the table below.

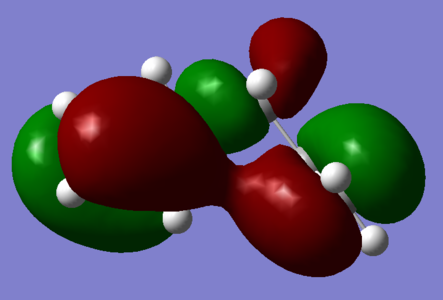
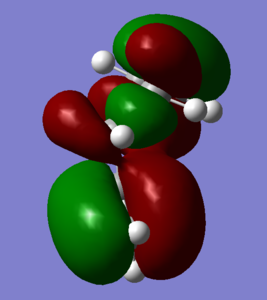
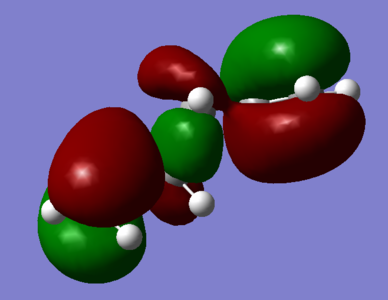
The energetic difference between the gauche and anti conformers produced is unexpected in the context of organic chemistry. This is because it is expected that having the bulky terminal alkenyl groups anti to each-other, with no spatial overlap will result in the smallest amount of steric clashes when compared to the gauche conformer where these groups have a much smaller torsional angle of 60°. This apparent contradiction can be rationalized by visualizing both the MO's of the gauche-3 and anti-2 conformers shown below. Looking at figure 1, the gauche-3 HOMO, the twist of the gauche leads to favourable in-phase overlap between the pi systems. In contrast this cannot possibly occur for the anti conformer due to their 180° relative orientations. A sigma-conjugation interaction between the vicuna C-H bond and the alkyl fragment in the gauche conformer can be seen, however by looking at figures 2 and 3 this interaction occurs in both conformers and is therefore not responsible for the gauche stability. A drawback of the calculations carried out is that the HF level of these neglects electron-correlation effects and effects such as the C-H alkenyl interaction are neglected to an extent when energetic calculations are considered.

Nf710 (talk) 09:47, 11 March 2016 (UTC) Nice use of the orbitals to explain the energy ordering

• 
  Figure 1; Gauche 3 HOMO: π-interactions between terminal alkenyl fragemnts due to 60° relative orientation
• 
  Figure 2; Gauche 3 HOMO-1: Vicinal acidic proton-alkenyl fragment sigma-conjugation
• 
  Figure 3; a) Anti 1 HOMO: Absence of any π-interactions between terminal alkenyl fragemnts due to 180° relative orientation b) some vicinal-alkenyl sigma-conjugation

Conformer & Level of theory	Optimized Structure	Energy (hartrees)	Relative energy (kcal/mol)	Calculation Summary	Point Group Summary
anti_1 HF/3-21g		-231.69260234	0.037
anti_2 HF/3-21g		-231.69253528	0.079
gauche_3		-231.69266122	0.000

[Note anti-1 point group was initially given as C2, but subsequent relaxation of point group constraints (default 0.01) and symmetrization yielded the C2 point group.]

Optimization of the anti-2 conformer using the B3LYP/6-31G(d) level of theory

As stated before the DFT level of theory unlike the previous calculations takes into account a larger basis set and will yield a more accurate optimization. The resulting structures geometry is similar, with the same Ci point group as expected, but resultant bond lengths and torsional angles do differ between the two levels of theory.

Conformer & Level of theory	Optimized Structure	Energy (hartrees)	Calculation Summary	Point Group Summary
anti_2 B3LYP/6-31G(d)		-234.61171035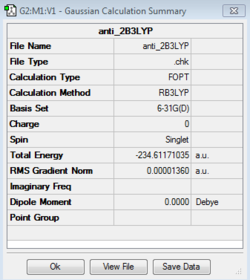

• 
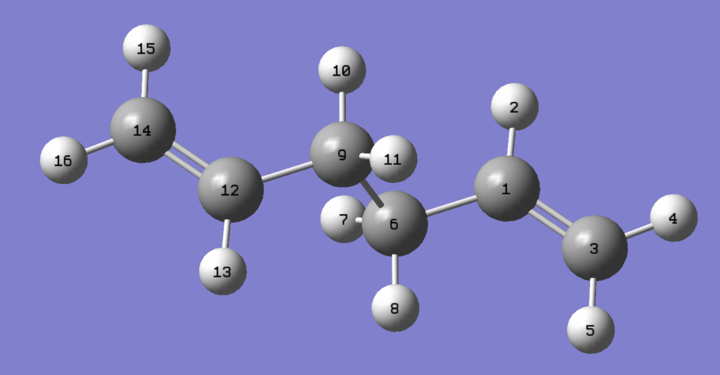
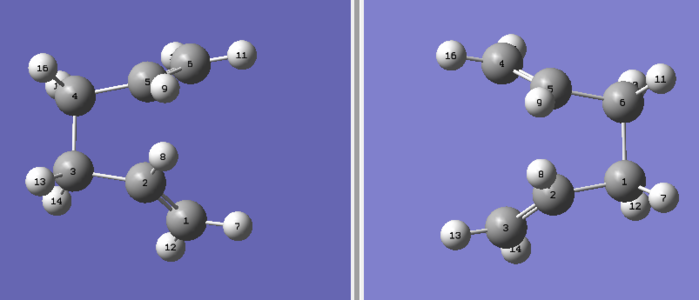
  Figure 4; Anti 2 Atomic labels for reference

Using figure 4 for atom reference the following tables depict changes in bond length, compared to literature electron diffraction methods, and for key carbon-carbon dihedral angles in the anti-2 conformer between the HF/3-21(g) and B3LYP/6-31G(d) levels of theory.

Dihedral angles

	Dihedral Angle (°)
Atom labels	HF/3-21G	B3LYP/6-31G(d)
C3-C1-C6-C9	114.67345	118.58844
C1-C6-C9-C12	179.99545	180.00000
C6-C9-C12-C14	-114.69826	-118.58779

Regarding dihedral angles because the anti-linkage along the C1-C6-C9-C12 bond axis was initially set to 180° and is expected not to deviate from this value during optimization, the B3LYP/6-31G(d) level of theory achieves this unlike HF indicating it is more accurate regarding this aspect. Furthermore the dihedral angles along the C3-C1-C6-C9 and C6-C9-C12-C14 which concern an sp²-sp³ linkage are closer to 120° and deviate less relative to each-other. This is expected for an alkene center where the optimal orbital arrangement would be 120° trigonal planar and therefore it is concluded that the HF/3-21G level of theory is less optimal for reproducing accurate dihedral angles in both cases.

Bond lengths

	Bond length (Å)
Atom labels	HF/3-21G	B3LYP/6-31G(d)	Electron Diffraction
C1-C3	1.31614	1.33352	1.34 ± 0.003
C1-C6	1.50886	1.50421	1.508 ± 0.012
C6-C9	1.55282	1.54808	1.538 ± 0.027
mean C-H	1.07971	1.09324	1.087 ± 0.002

It is immediately seen that the B3LYP/6-31G(d) calculated values of the C1-C3 C=C, C6-C9 C-C bond lengths are in far greater agreement with literature values than values from the HF calculations. The reason the higher level of theory calculates a more accurate and shorter C=C bond value is because it accounts for electron-correlation energies and takes into account polarization to a greater extent. This is key as HF approximates using single slater determinants and orbital wavefunctions to model electron density across the molecule introducing Coulombic term errors. This approximation is seen to be more important for bonds consisting of less core-like sp² hybridized carbon atoms causing HF to underestimate it by a larger 0.02386Å.

In contrast this trend did not hold when it came to the C1-C6 bond which contains only one sp² orbital is only in better agreement with HF with a value of 1.50886Å compared to the shorter and less accurate 1.50421Å calculated using B3LYP/6-31G(d). The C6-C9 bond is fully contributed to by sp³ orbitals, here HF overestimates the bond length by a greater extent.Regarding C-H bond lengths literature only states the mean length and therefore any arguments concerning which level of theory optimizes these better is hard to justify.

To conclude HF theory tends to underestimate bond lengths regarding bonds that involve the overlap of more core-like sp² orbitals, but overestimate bonds containing only sp³ orbital overlap. However the quantitative geometric discrepancies between the two levels of theory are very small, the maximum relative difference between the two levels of theory is seen to be 0.013Å. Therefore it can be deduced that the degree of polarization taken into account is only significant for larger/more complex molecular structures for example those containing hetero-atoms and not in the case of 1,5-hexadiene. Overall B3LYP/6-31(d) results more accurately reproduced electron diffraction values. See figure 4 for an atomically labelled diagram. To the extent that HF is in error, it tends to overestimate the occupation of bonding orbitals, thus errors tend to be in the direction of predicting bonds to be too short. However the effects of this are seen in this report to be effected by the hybridization of such orbitals.

It is identified that HF's failure to take into account for dispersion tends to predict transition species (non-bonded complexes) to be too 'loose'. DFT does not encounter such errors as much and because of this DFT, and not HF, will be seen in the proceeding sections to provide a more accurate ab-initio optimization of transition state structures.

Frequency and thermochemical analysis at varying temperatures

Frequency calculations were carried out on the DFT optimized anti-2 conformer, calculating force constants only once. This is necessary in order to locate the PES minimum structure, which by nature will contain no imaginary (negative) vibrational frequencies. These frequencies only occur when the second derivative of the molecular force constant with respect to the Cartesian nuclear coordinates via transformation to mass-weighted coordinates is negative. A negative frequency means that the current geometry is that of a PES maxima (transition-stat [single]) a reaction/geometric change toward a global minima will occur, this is demonstrated mathematically in the next section. The frequency calculations were carried out in the temperature range of 0-400K (by modifying the .gif input file manually) in order to quantify changes in molecular energy and enthraply contributions with temperature. All frequencies were found to be real and positive meaning that the true PES minimum for the anti-2 conformer of 1,5-hexadiene was located. Gaussian calculates all the following values using 1,5-hexadienes statistical mechanical molecular partition function that quantify translational, rotational, vibration and electronic DoF contributions.

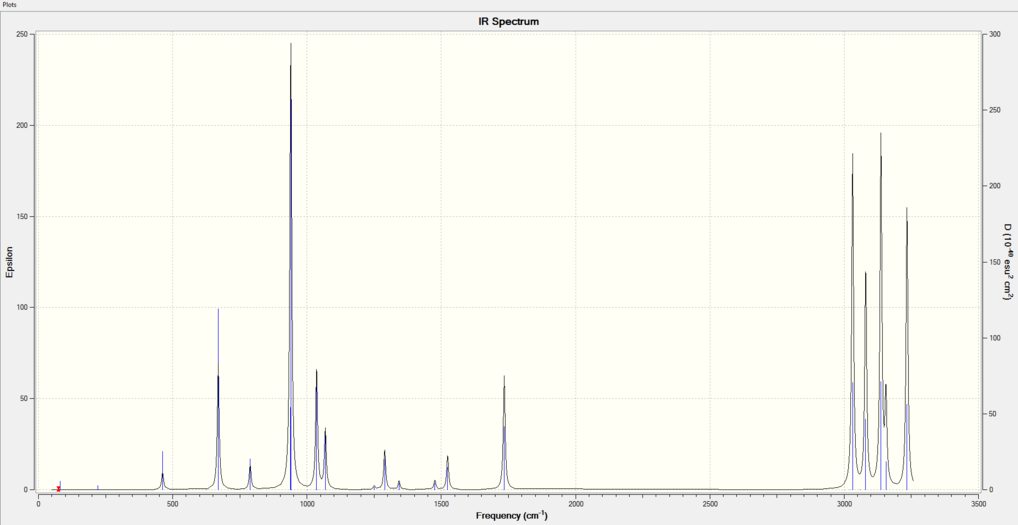
All frequencies are shown in the IR spectrum below for 0.001K. Note this was visualized for all temperatures but because frequency calculations carried out do not act to optimize the structure at different temperatures, geometry and bond distances were not altered and hence no change to the spectrum was seen from 0.001-400K. Selection rules dictate that IR active vibrations must undergo a change in dipole moment and hence 1,5-hexadiene observes polarization, which is why the B3LYP/6-31G(d) level of theory are far better suited to carry out these calculations as opposed to HF. Note that the temperature of 0.001K was used because Gaussian does carry out frequency analysis at absolute zero.

• 
  Figure 5: IR spectrum of 1,5-hexadiene anti-2 conformer at 0.001K

Temperature (K)	Sum:electronic and zero-point energies (a.u.)	Sum:electronic and thermal energies (a.u.)	Sum:electronic and thermal enthalpies (a.u.)	Sum:electronic and thermal free energies (a.u.)
0.001	-234.469204	-234.469204	-234.469204	-234.469204
100.00	-234.469204	-234.467728	-234.467412	-234.477393
200.00	-234.469204	-234.465264	-234.464631	-234.488377
298.15	-234.469204	-234.461857	-234.460913	-234.500777
400.00	-234.469204	-234.457070	-234.455803	-234.515146

These different tabulated values take into account more corrections for the exact system free energy from left to right. Firstly the zero point vibrational energy ZPVE, is calculated from vibrational motion at 0 K for a quantum harmonic oscillator model as a sum of contributions from all i vibrational modes of the system. Secondly the thermal energies Etot, this is the energy of 1,5-hexadiene relative to separate nuclei and electrons consisting of the internal energy contributions due to excitation of 1,5-hexadienes DoF. The thermal enthalpies correction now takes into account the systems molar thermal energy RT and the thermal free energies takes into account entropic contributions from 1,5-hexadienes DoF.

Predictably at 0.001K, the contribution from the thermal contribution was effectively zero, and this and entropic contribution to the system energy increased as the system temperature increased producing an easily visible trend. Further investigation could be carried out to quantify the anharmonicity in the system as this is generally an important relaxation of the harmonic oscillator approximation for real systems at higher temperatures.

Note: thermochemical properties were calculated only with explicitly consideration of 10(400K), 7(200K), 3(100K), degrees of freedom as vibrations may cause significant error.

Optimizing the Chair and Boat transition structures

In this section the Cope Rearrangements chair and boat transition state structures are produced and optimized in Gaussview 5.0. The first step involves optimizing the allyl fragments of such transition states at the HF/3-21G level of theory, a pair of these will be required in order to produce both transition states. Then TS(Berny) and frozen coordinate with subsequent hessian derivative methods will be used to optimize the chair structure and interpolation by QST2/3 for the boat structure. Each pair of methods resulting structure geometries are compared and the success of each to locate their respective transition states will be determined by the presence of a characteristic imaginary frequency. Further to this the DFT level of theory will be used to re-optimize and compare both transition state structures and reaction pathway activation energies.

Optimizing the allyl fragment of 1,5-hexadiene

The HF/3-21G optimized CH2CHCH2 allyl fragment is shown below, its point group is C2v and as expected for a resonance radical structure, all carbon-carbon bond lengths are identical in length, 1.39Å. The structures energy was found to be -115.832039971 (Hartrees).

Jmol structure

Optimizing the chair transition state

Firstly the TS(Berny) optimization of a guess transition state chair structure was performed. This method directly optimized to a transition state structure. The main approximation of this method is clear as it assumes the manually generated chair geometry input is close enough to that of a real chair transition state energy maximum geometry. Computationally this method is fast, but very error prone due to this dependence on the initial starting input. This risk is quantified by the fact an ideal chair transition state for the Cope rearrangement is 2.2Å for allyl fragment terminal carbon inter-fragment distance, whereas the input file used in this report a length of 2.20973Å was used. This slight deviation could have been significant as transition state geometries are harder to optimize than for PES minima structures - reactant or product. This is because they represent a finite saddle point on a reaction PES such that convergence on them and obtaining a single imaginary frequency requires more precise starting geometries.

Despite this a chair structure was converged upon and subsequent analysis of the frequencies obtained for the Opt+Freq calculation yielded a single imaginary frequency of -817.90cm^-1.

Secondly the frozen coordinate method was used, unlike the TS(Berny) method it optimizes in two steps and in both toward a minimum. This may seem counter-intuitive but this optimization requires constraints on the input structure in the form of fixed bond forming/breaking sites between the allyl fragments such that a product cannot be formed, and was set to 2.2Å. The rest of the structure is relaxed relative to these frozen coordinates (between C1-C14 and C6-C9) and subsequent hessian derivative optimization of the initially frozen coordinates allows the transition state structure to be converged upon. Once again a chair transition state structure was obtained and its characteristic single imaginary frequency in this case was -817.82cm^-1.

• 
  Figure 6; Atomic labels for comparing the TS(Berny) and Frozen coordinate chair TS bond lengths

In both cases the input files were cleaned and symmetrized to the C1 point group and force constants were calculated once (except for the subsequent frozen coordinate derivatives) to have the best chance of convergence to the chair transition state.

Transition state structure	Optimization Method	Energy (hartrees)	Imaginary Vibrational frequency (cm-1)	Visualized Im-frequency (leads to reaction)
Chair of the Cope Rearrangement	TS(Berny)	-231.61932244	-817.90	Vibration that leads to a reaction
Chair of the Cope Rearrangement	Frozen coordinate	-231.61932220	-817.82	Vibration that leads to a reaction

For both optimization methods the imaginary frequency obtained are of very similar magnitude and both correspond to a vibration consisting of antisymmetric elongation and contraction of terminal allyl carbon pairs. This asymmetry refers to a reaction that leads to the forward and reverse Cope Rearrangement. Furthermore each method yielded a C2h point group symmetry characteristic of the chair transition state.

Imaginary frequencies can be explained in terms of the quantum harmonic oscillator where vibrational frequency is expressed using the following relation:

$v=\frac{1}{2\pi }\sqrt{\frac{k}{\mu }},$

As explained before an imaginary frequency is given by a negative second derivative of the force constant, which constitute the systems hessian matrix. Diagonalized eigenvalues are obtained, which are squared harmonic frequencies of normal vibrations. Physically, a negative eigenvalue corresponds to negative curvature of corresponding normal reaction coordinate such that the geometry on which this second derivative is yielded is passing through a saddle point. This point can also be characterised by stating that in one direction in nuclear configuration space the energy has a maximum, while in all other orthogonal reaction coordinates the energy is a minimum. Visualizing a 1D PES for a reactant minima, the concavity on both sides is upward and this constitutes a positive force constant, pulling vibrational structures back toward the local minima and no reaction occurs. In contrast a saddle point in all directions is concave down leading to a negative force constant and hence a negative imaginary frequency that leads to a reaction.

Comparison of chair TS geometries for TS(Berny) and Frozen coordinate

The following table gives values for the key bond-forming and bond-breaking interatomic distances during the Cope Rearrangement for both TS(Berny) and FC methods. It is useful as a tool to determine the importance of computing force constants, of which was not done for the final FC chair structure.

Atomic labels	Berny(TS) optimization (Å)	Frozen coordinate optimization (Å)
C1-C14 (bond making/breaking)	2.02022	2.02079
C6-C9 (bond making/breaking)	2.02011	2.02040
C4-C12	2.87883	2.87942
H3-H16	2.54557	2.54637

Firstly for all bond lengths tabulated it is seen that the FC method yields longer bond lengths, but the differences are small and deviations are all within an accuracy of 0.002Å. The key bond forming/breaking interatomic distances are very similar and as a result we can conclude that both methods of optimization produce the same chair transition state structure. Furthermore discrepancies between the methods such as FC not computing force constants during final optimization and the initial guess of the TS(Berny) input can be considered negligible for 1,5-hexadiene, a simple non-polar molecule. Values for internal allyl C-C and axial hydrogen interatomic distances are included to obtain an overall geometric picture to compare both chair transition states.

Optimizing the boat transition state

In this section the Cope Rearrangement Boat transition state will be optimized using the QTS2 method at the HF/3-21G level of theory. This required the structures of the reactant and the product and the use of a synchronous transit-guided quasi-Newton approach to generate an initial guess and optimize it to the transition state. QST2 achieves this by linear interpolation along the parabola connecting the reactant and product structures and often only works well for well-defined inputs where a good guess structure is produced. The guess TS by definition is exactly half way between reactant and product geometries and as such good inputs are required.

Initially a HF/3-21G optimized Ci anti-2 conformer of 1,5-hexadiene was used as an initial reactant and product input for the QST2 method. This required specific labeling of atoms as seen in figure 7. However the linearly interpolated transition state was that of a dissociated chair. This was not the transition state we were looking for and therefore informs that the initial input geometries are not close enough to that of a boat, this is analogous Hammond's postulate. To remedy this the initial anti-2 conformers internal C2-C3-C4-C5 dihedral angle was set to 0° and the inside C1-C2-C3/C4-C5-C6 angles were both set to 100°. The initial inputs now resemble a boat much more as seen in figure 8.

• 
  Figure 7: Dissociated Chair transition state
• 
  Figure 8: Initial atom labelled QST2 inputs that generated a Boat transisiton state

Transition state structure	Optimization Method	Energy (hartrees)	Imaginary Vibrational frequency (cm-1)	Visualized Im-frequency (leads to reaction)
Boat of the Cope Rearrangement	QST2	-231.602802136	-840.1357	Vibration that leads to a reaction

As discussed the presence of a single imaginary frequency is wholly characteristic of a transition state. This occurred for the QST2 method at -840.1357cm^-1. Similarly to the chair transition state this vibration consists of the asymmetric elongation and contraction of the terminal bond breaking/making allyl fragment carbon atoms. Furthermore the QST2 method yielded a structure with C2v point group symmetry characteristic of the boat transition state.

Subsequent use of the QST3 approach is expected to be more robust than QST2 as it overcomes problems due to poor interpolated guess structures. However computationally it is only ever utilized when convergence on the transition state is difficult which was not the case in this report, and hence QST3 optimizations were not carried out.

Note: The advantage of transit-guided quasi-Newton approaches over the eigenvector following methods is that a full evaluation of second derivative matrix is not needed. For example TS(Berny) requires second derivatives is high computational cost and in practice algorithms that calculate the Hessian once and then update it during the search.

However because these approaches do use approximate guess Hessians that might differ significantly from the true Hessian, a better investigation would contain subsequent full second order derivative calculations, for example using the DFT level of theory, to verify the boat structures obtained.

Intrinsic Reaction Coordinate (IRC) analysis

The "IRC represents the mass-weighted steepest descent path on the potential energy surface (PES), starting from the transition structure (TS)"., this is done using nuclear positions in Cartesian space. In essence the IRC is an algorithmic calculation of a series of points at which the energy gradient is largest, using force constants leading from imaginary frequencies. Calculations start from the transition state geometry at IRC=0 and then steps are taken sequentially using this approach until a local minimum adjacent to the initial TS geometry is reached. Because the Cope rearrangement is symmetrical i.e. the reactant and product are identical, the IRC is computed in only one reaction coordinate direction to save computational time. Force constants are calculated at every step of which initially 50 are used. IRC plots are shown in the table below for both chair and boat transition states. Convergence of the IRC was verified at 50 steps for the chair and 150 steps for the boat. Calculating for steps larger than these is pointless as once converged the IRC doesn't change. Note that the RMS gradient of the IRC can also be used to verify an initial transition state geometry because at a maxima (transition state) or minima (product) the gradient is zero. All IRC calculations were carried out using the HF/3-21G level of theory as this must match the level of theory used to optimize the transition state inputs to it.

The IRC provides a unique insight into the connection between a transition state two local minimum structures (MINs) conformers of 1,5-hexadiene for the Cope Rearrangement.

• For the chair transition state it was found that a Gauche-4 conformer is converged upon, with C2 point group.
• For the boat transition state it was found that a Gauche-3 conformer is converged upon, with C2 point group.

Transition state	Number of Steps	IRC Path	Final Conformer	Final Conformer Total Energy (Hartree)
Chair	50	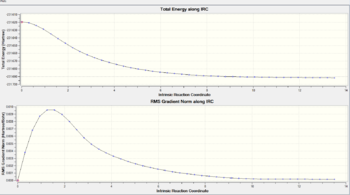IRC path evaluated at 50 points for the chair transition state- 1,5-hexadiene during Cope Rearrangement	Gauche-2	-231.69157907
Boat	150	IRC path evaluated at 150 points for the boat transition state- 1,5-hexadiene during Cope Rearrangement	Gauche-3: 1,5-hexadiene	-231.69263195

Because the IRC is known to unstable due to PES valley-ridge inflection as it may introduce a bifurcation point which introduces a set of different dynamical trajectories not seen by the IRC (1D) due to molecular vibrations tangent to the IRC coordinate. Therefore to circumvent the IRC convergence issue, the final intermediate structure from each IRC is re-optimized for both transition states as this does take into account bifurcation points.

• Chair: Chosen to re-optimize the last intermediate IRC structure, no.44. The force constant was calculated once in the Opt+Freq command in the HF/3-21G level of theory.

Last intermediate structure (44)	Resulting conformer Jmol structure	Bond length variations
		IRC path evaluated at 50 points for the chair transition state- 1,5-hexadiene during Cope Rearrangement

This has yielded Gauche-2 as the product conformation. This is a different result than for the IRC which after convergence was closer in energy to a Gauche-4 conformer. The bond length variations plot for the Cope Rearrangement provides a nice graphical interpretation of the bond variation along the IRC. As seen the key bond breaking/making distances (C1-C14 and C6-C9) are always the longest and transition between no bond and new C-C bond during the [3,3]-sigmatropic rearrangement. Furthermore the transition between C=C and C-C bonding between C6-C4 and C4-C1 can be seen. All of these pairs intercept at an IRC value of 44 which corresponds to the transition state geometry (at 44 due to mirrored data in excel).

• Boat: Chosen to re-optimize the last intermediate IRC structure, no.74. The force constant was calculated once in the Opt+Freq command in the HF/3-21G level of theory.

Last intermediate structure (74)	Resulting conformer Jmol structure

This has yielded a gauche-3 conformer, which corresponds to the actual global conformer minimum for the Cope Rearrangement.

Nf710 (talk) 09:51, 11 March 2016 (UTC)Very nice use of the python code

Activation energies of the Cope Rearrangement

Firstly both the chair and boat transition state structures are re-optimized using the DFT (B3LYP/6-31G*) level of theory. In both cases using the higher levels of theory still resulted in single imaginary frequency vibrations being obtained; boat, -530.3735cm^-1, and chair, 565.5419cm^-1, as seen in the Jmol structures in the table below. Data from these optimized structures will be used to calculate the activation energies for the Cope Rearrangement of 1,5-hexadiene.

B3LYP-6-31* optimized boat Imaginary frequency vibration	B3LYP-6-31* optimized chair Imaginary frequency vibration

To decide which conformer to use to derive the activation energies for the Cope Rearrangement through either chair or boat transition states it is important consider evidence from the IRC analysis conducted in the previous section. It is key to understand that the IRC is one-dimensional along the reaction coordinate and its convergence along the PES has its limitations. This 1D path prevents it from reaching a true minimum as in 1D the energy would have to increase after convergence. This is the reason why chair transition state IRC converged on a gauche-4 conformation. However during subsequent optimization in 2D, a bifurcation point is now permitted such that in 2D the total energy can decrease causing convergence on the gauche-2 conformer. However it is known that the lowest energy conformation is the gauche-3, and therefore this is the most ideal product/reactant to calculate activation energies for this symmetrical reaction as transition-state-theory dictates transition state activation energy from absolute minima structures of reactants.

A better investigation to generate accurate activation energy values would be through connecting conformers i.e. through gauche-3/2 and not anti-2. Anti-2 was initially calculated to save simulation time as optimizations were carried out previously. This surmounts to an approximation as all the conformations of 1,5-hexadiene are linked through internal dihedral C-C bond that are within thermal energy perturbation scales. Furthermore when comparing the Cope-rearrangement activation barrier through either the chair or boat transition state geometries with the barrier for conformer interconversion, the latter is fairly insignificant. This means the error introduced by calculating the Cope activation barrier from any of the possible conformation reactants is insignificant. However values calculated in this report will be from both the anti-2 and gauche-3 conformations to quantify this.

The following structures, optimized using the HF/3-21G level of theory are all re-optimized using DFT; Chair TS, Boat TS and both the anti-2 and gauche-3 conformers of 1,5-hexadiene. Subsequent frequency analysis in the temperature range 0.001K-400K was carried out on each newly optimized structure and thermochemical analysis results are shown in the table below. This method of subsequent optimization and frequency analysis using a higher level of theory saves computational time and yields very accurate results for the time taken.

	HF/3-21G				B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Sum of electronic and thermal energies
		at 0.001 K	at 298.15 K	at 400.00 K		at 0.001 K	at 298.15 K	at 400.00 K
Chair TS	-231.619322	-231.466699	-231.461340	-231.457293	-234.556983	-234.414929	-234.409009	-234.404522
Boat TS	-????	-231.450925	-231.445298	-231.441147	-234.543093	-234.402342	-234.396007	-234.391328
Anti-2 conformer	-231.692535	-231.539540	-231.532566	-231.528179	-234.611710	-234.469204	-234.461857	-234.457070
Gauche-3 reacting minima conformer	-231.692661	-231.539486	-231.532646	-231.528274	-234.611329	-234.468693	-234.461464	-234.456687

Using the data concerning each structures zero-point energies and thermal energies contributions activation energies for the Cope Rearrangement can be derived by simple subtraction of TS energies from product conformer energies at a particular temperature. The results of this are shown in the table below. Note these are relative energy values and as such units of kcal/mol will be used as opposed to atomic units for ease of comparison between results.

	HF/3-21G	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 400 K	at 0 K	at 298.15 K	at 400 K
Anti-2: ΔE (Chair)	45.7084274	44.6949993	44.4816461	34.0580840	33.1626278	32.9743749	33.5 ± 0.5
Anti 2: ΔE (Boat)	55.6067639	54.7615085	54.6134162	41.9565474	41.3215080	41.2537367	44.7 ± 2.0
Gauche-3: ΔE (Chair)	45.6745418	44.7452001	44.5412595	33.7374266	32.9160165	32.7340387	33.5 ± 0.5
Gauche-3: ΔE (Boat)	55.5728784	54.8117092	54.6730296	41.6358900	41.0748964	41.0134005	44.7 ± 2.0

It is seen that activation energies derived using the higher DFT level of theory prove to be in much better agreement with literature values. As seen before ground state energy differences between the two levels of theory, for example for the anti-2 conformer; -231.69253528 a.u (HF) and -234.61171035 a.u (DFT) do not account for the larger differences in activation energies. Therefore this difference lies in the fact that the HF/3-21G level of theory did not optimize the transition state structures as accurately. This can be attributed to HF's neglection of electron-correlation energies due to the use of single electron wavefunctions to approximate the total multi-electron wavefunction for the structures in question. This destabilises the transition states relative to the reactant conformers leading to increasing activation energies for all data points tabulated.

Another key result is the decreasing trend in activation energy for both conformers and both transition states at higher temperatures. This is because the presence of thermal energy, RT (molar), in the system means that the intrinsic molecular energy input required in the reactant conformers is less i.e the relative energy difference between the reacting conformers and this transition state is reduced, hence the activation barrier is reduced at higher system temperatures. In addition it is clear that Cope Rearrangements proceeding via a chair transition state have far less activation energy than those transitioning via a boat. Remembering the Arrenhius equation for kinetically controlled reaction rates these two factors determine that a Cope Rearrangement via a chair transition state has a faster rate is the preferred reaction pathway and that this rate only increases with temperature.

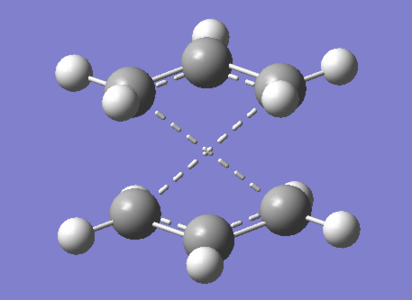
Two factors can be seen to govern the chair transition states favourability when compared the boat. Firstly sterics - it is widely accepted that the strain involved in the chair geometry is lower than that in a boat. Studies of acyclic Cope rearrangements confirm this as the calculated 6kcal/mol preference mirrors that of cyclohexane chair and boat conformation stability. Secondly orbital electronics - when examining both transition states with a frontier orbital description it is clear that the chair TS is favored due to a larger distance/lower in-space overlap of the anti-bonding interaction between the two allyl fragment central carbon p-orbital lobes compared to in boat transition state seen in figure 9. Essentially a Cope rearrangement passing through the chair TS path these key orbitals are too far away in space to interact lowering the TS energy and increasing the rate of reaction via this reaction pathway.

• 
  Figure 9: Cope rearrangement: Exo and Endo TS extent anti-bonding FO interactions (adopted from Ian Flemming's 'Frontier Orbtials in Organic Chemistry')

As discussed the relative energies of the transition states resulting from the HF and DFT levels of theory differ to a significant enough extent. In contrast the table below does show that the actual geometries of both the chair and boat transition states obtained from either method do not differ greatly at all.

		HF/3-21G	B3LYP/6-31G(d)
Boat T.S	Allyl fragments separation (‎Å)	2.13971	2.20661
	Allyl C-C Bond (‎Å)	1.38142	1.39323
Chair T.S	Allyl fragments separation (‎Å)	2.02022	1.96755
	Allyl C-C Bond (‎Å)	1.38931	1.40750

Tabulated values for the terminal allyl carbon bond making/breaking distances and internal fragment C-C resonance distances show a maximum deviation of 0.067Å (chair) and 0.053Å (boat). These differences are larger than for when the anti-2 conformer was optimized using the two methods in section 2.3.4, where the maximum discrepancy was 0.013Å. However this is expected for a transition state geometry optimization as convergence is more difficult. Overall it can be concluded that either level of theory, and the lower 3-21G basis set used in HF, can be used to compute accurate chair and boat transition state structures with a high level of accuracy. However energies deviated to a more significant extent, as demonstrated by large activation energy differences. Both of these factors must be weighted relative to the nature of the problem to decide which method to use during future computations.

Nf710 (talk) 09:54, 11 March 2016 (UTC) you have gone beyond the script and worked out the activation energies for different conformers, you have also shown a fairly high level understanding of the theory and posed questions where to take this work further. well done this is a very good report.

The Diels Alder Cycloaddition

Prelude

In this section of the report two separate Diels-Alder cycloaddition reactions will be investigated. Firstly the prototypical Diels-Alder reaction between cis-butene and ethylene(fig. 10), where a Diels-Alder transition state is first computed, analysed and compared to literature. This is followed by the Diels-Alder reaction between cyclohexa-1,3-diene reaction with maleic anhydride(fig. 11), where substituents are introduced onto the dieneophile fragment, imparting endo/exo transition state stereo-selectivity, the preference of which will be investigated.

The Diels-Alder reaction is a [4+2]π cycloaddition of two key reactant species; a diene, and a dienophile. The general consensus is that it proceeds via a syn-concerted 6-membered pericylic transition state. This generally justifies both diene and dienophile stereospecifity, however computational studies have postulated a diradical intermediate . Because the reaction is pericylic, like that for the Cope Rearrangement, its mechanism must obey the strict Woodward-Hoffmann orbital symmetry conservation rules. The computed reactions are all thermally allowed as (4q + 2)s +(4r)a = 1, is odd. In both reactions the diene is a π4s component and the dienophile is a π2s component, note; the suffixes 'a' and 's' stand for antarafacial and suprafacial respectively.

Figure 10; Prototypical Diels-Alder cycloaddition

Figure 11; Stereoselective Diels-Alder cylcoaddition

As for many reactions the energetic favourability for a reaction is determined by the frontier orbitals in the system. For π-conjugated systems the diene component will have a higher energy HOMO due to more extensive conjugation seen using Huckel theory and the dieneophile component will have the higher energy LUMO. In general these FO's exhibit the closet energetic match and the most facile reaction pathway. This consensus holds for all prototypical and the majority of substituted Diels-Alder reactions and constitutes normal electron demand. Frontier orbital energetics can be improved upon, and rates increased, with a more electron rich diene and more electron poor dieneophile to reduce the FO energy-gap. This is seen in the second study with increased hyper-conjugation into more substituted C=C bonds in the diene and the introduction of α-lactone electron withdrawing groups in the dieneophile.

All calculations in this section are carried out using semi-empirical/AM1 methods. Semi-empircale methods, as opposed to ab-initio methods, such as Hartree-Fock, where basis sets of the Schrodinger equation are used, are much faster computationally. The main reason for this is the Zero Differential Overlap (ZDO) approximation where two-electron Hamiltonians are not explicitly defined, simplifying the Hartree-Fock secular equation. In this report only π MO's derived from Huckel theory are considered which equates to a neglection of the two electron Hamiltonian. This constitutes ignoring certain iterative integrals such as two-electron repulsion integrals. Remarkable computational time is saved - if N orbitals are used in a calculation, the number of two-electron repulsion integrals scales as N⁴, however this is reduced to N² using the ZDO approximation. In order to compensate for these approximations results obtained are parametrized and fitted against a database of molecules. Note the AM1, otherwise known as the Austin Model 1, is based upon the Neglect of Differential Diatomic Overlap, NDDO, which is very similar to the ZDO approximation except that it adds all two centre integrals for repulsion between a charge distribution on one center and a charge distribution on another center to increase calculation accuracy.

(Well-worded introduction Tam10 (talk) 11:35, 11 March 2016 (UTC))

Diels Alder cycloaddition of cis-butene and ethylene

Optimization of the cis-butene diene component

Before the Diels-Alder transition states can be analysed its component reactants must first be optimized for use later use in a guess structure for the exo/endo structures. Firstly the cis-butadiene reactant was optimized, this required the use of four trivalent (S-S-D) carbon fragments, dihedral angle modification from 180° to 0° and subsequent optimization at the semi-empirical/AM1 level of theory, the results are shown below. All frontier orbital symmetry considerations are explicitly with respect to the bisecting C-C single bond clearly shown in the center of all diagrams.

Jmol Structure	Energy (Hartrees)	Point Group
	0.04879719	C2v

(Be careful as this isn't the minimised structure for cis-butadiene. There will be an imaginary frequency corresponding to the twist away from a dihedral angle of 0º. I can see that you've used script to include the correct bonding Tam10 (talk) 11:35, 11 March 2016 (UTC))

Both the C=C and C-C bond lengths resulting from AM1 optimization are in good agreement with ab-initio methods - 0.134/0.145Å compared to 0.1341/0.1457Å.

From the frequency analysis carried out the HOMO and LUMO can be visualized below;

Cis-butadiene: HOMO MO	Cis-butadiene: LUMO MO
HOMO MO: optimized cis-butadiene showing antisymmetry with respect to the plane	LUMO MO: optimized cis-butadiene showing symmetry with respect to the plane

Optimization of the ethylene dienenophile component

Similarly an ethylene reactant component, made out of two trivalent (S-S-D) carbon fragments, was also optimized at the AM1 level of theory, results are shown below.

Jmol Structure	Energy (Hartrees)	Point Group
	0.02619028	D2h

Again the C=C bond length for ethylene after AM1 optimization is in good agreement with ab-initio calculations - 0.133Å compared to 0.1331Å.

From the frequency analysis carried out the HOMO and LUMO can be visualized below;

Ethylene: HOMO MO	Ethylene: LUMO MO
HOMO MO: optimized ethylene showing symmetry with respect to the plane	LUMO MO: optimized ethylene showing antisymmetry with respect to the plane

Optimization of the Diels-Alder transition state

To generate exo/endo transition state structures, the TS(Berny) method, as seen for the Cope-Rearrangement chair transition state, will be used. To do this again requires the 'guessing' of both transition state geometries. Transition state geometries lead onto reactive trajectories and yet again operate rely upon the electron availability, and in the case of Diels-Alder the reaction, at the reaction centers through perturbations of the σ- and π-bonds. Essentially, as seen for most pericylic reactions this corresponds to the case where maximum overlap of π-electron density can occur. This occurs when the diene and dienophile fragments are positioned in an envelope-type orientation. The distance between reactive terminal carbon centers was set equal to 2.24Å, the structure subsequently cleaned and symmetrized. This allowed the creation of an initial input guess that on the reaction PES was near enough the local, synchronous transition state, as to not diverge back to the separate reactant state of the system. The resulting transition state is shown below, note there is no endo/exo preference as both diene and dienophile components are prototypical.

Jmol Structure	Energy (Hartrees)	Point Group
	0.11165479	C1

From the frequency analysis carried out the HOMO and LUMO can be visualized below;

Diels-Alder TS: HOMO MO	Diels-Alder TS: LUMO MO
HOMO MO: optimized Diels-Alder TS showing antisymmetry with respect to the plane	LUMO MO: optimized Diels-Alder TS showing symmetry with respect to the plane

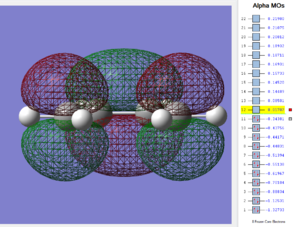
By inspection it is seen that as expected from normal-electron demand the transition state HOMO consists of the in-phase combination of cis-butenes HOMO and ethylenes LUMO. These are both antisymmetric with respect to the C-C plane and are best energetically matched to interact, ΔE=0.39664 (Hartrees). Further computational studies of the mechanism tell us that initially butadiene would be in s-trans configuration which upon approach of the dieneophile would transform into the less populated Gauche form and subsequently the syn-planar form as inputted in this report. This allows the RC to approach the TS saddle point in a way that maximises π-π overlap, between ethylenes π* MO and butadienes π HOMO. The resulting transition state is Hückel aromatic, near which all C-C adopt a value of 1.397 Å. Analogously the symmetric HOMO of ethylene and the correspondingly symmetric LUMO of syn cis-butene form the transition state LUMO. These two overlaps become the two new sigma bonds in the product.

Following analysis of the vibrations, the transition state is confirmed by the presence of a single imaginary frequency at -954.18cm^-1 and is visualized below. This particular vibration leads to a reaction because of synchronous in phase-vibrations of both the diene and dienophile C=C terminal carbon atoms. This leads to a thermally allowed orbital energy crossing. If a charge transfer diagram were constructed between cis-butenes HOMO and ethylenes LUMO the TS's mechanistic importance is seen - at the TS the distorted diene, due to the electrophillic attack of the dienophile, converts from nucleophilic to electrophilic character. This results in a switching of the HOMO character along the reaction coordinate and is a result of the pyramidolization (deformation of a trigonal planar molecule into a tetrahedral arrangement) of the terminal CH2 bonds in both the diene and dienophile components, of which can be seen in the imaginary frequency. Therefore the significance of the Diels-Alder transition state can be regarded as a charge-transfer switching arrangement.

In contrast to this the first positive frequency, also referred to as the orthogonal frequency, at 146.58 cm^-1, shows no pyramidolization of terminal CH2 centers. This is because corresponding vibrational mode, an asynchronous twisting of the diene and dienophile fragments, with no significant perturbation of the terminal σ-bond forming end internuclear distances, and therefore does not allow significant charge transfer/overlap from the diene HOMO to the dienophile LUMO. As a consequence this mode will not lead to a trajectory that will cross the transition state saddle point.

Only decoupled vibrational modes are considered and are therefore all normal on the RC. Only one negative vibrational mode/eigenvalue will exist at a transition state where this corresponds to negative curvature of corresponding normal coordinate, and therefore a negative force constant. Therefore these non-reactive vibrations are expected for all positive frequencies.

Furthermore this particular vibration leads to the reduction electrostatic attractions on the endo side of ethylene by rotation at the C5C6 axis, endo H atoms up, exo H atoms down

Diels-Alder TS Imaginary frequency vibration	Diels-Alder TS First positive frequency vibration
Imaginary vibrational frequency: -954.18 cm-1	First positive vibrational frequency: 146.58 cm-1

Figure 12; Atomic labels for comparing the Diels-Alder TS bond lengths

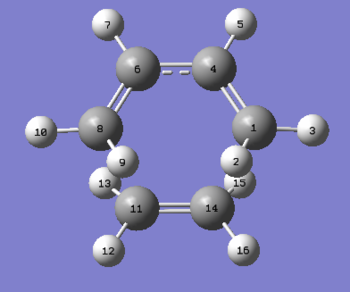
Atomic labels	Semi-empirical/AM1 Diels-Alder TS optimization (Å)	Literature (Å)
C8-C11 (partial bond)	2.11971	2.27
C1-C14 (partial bond)	2.11970	2.27
C4-C6	1.39755	1.41
C6-C8	1.38152	1.38
C11-C14	1.38253	1.39

Literature values were calculated from the time-resolved mechanism by quasiclassical trajectories at 298 K, with the saddle point of interest optimized at B3LYP/6-31G(d).

We can further probe the transition state by analyzing its geometry, in particular bond distances such as those being formed between the cis-butene and ethylene fragments. Firstly comparing AM1 calculated transition state bond distances with DFT, we can see that overall values are similar, with maximum deviation = 0.1503Å, corresponding to a percentage error of 6.62%. This maximum corresponds to the bond lengths between terminal carbons of the diene and dienophile where σ-bonding occurs. As stated before this is due to the frontier orbital overlap of cis-butene and ethylene to form the HOMO and LUMO in the transition state where charge transfer can occur. As a bond is usually defined as two atoms approaching closer than the sum of their Van der Waal radii, and this distance, C8-C11/C1-C14 = 2.11971/2.11970Å is far less than the sum of two carbon atoms Van der Wall radi, determined by Rowland in 1996, = 2 x 1.77Å = 3.54Å, we can conclude a bonding interaction/FO overlap is occurring.

Furthermore we can analyse the Hückel aromatic character of the transition state by inspecting the C=C bonding, of which are expected to be of intermediate bond length between single and double. It is known that typical sp²-sp²/sp³-sp³ carbon carbon bond lengths are approximately 1.34 Å/1.54 Å. All partial bonds in the transition state agreed well with DFT literature calculations and held values in the range of 1.38152-1.39755Å. This is intermediate with respect to standard single and double bond lengths and confirms this feature. It is expected that the Diels-Alder reaction will proceed synchronously, especially in the case of symmetrical reactants, and in this case all bond lengths involved in the concerted transition state should be of equivalent length. This is seen to a large extent with respect to the partial σ and π bonds. This corresponding equalization of bond lengths is also in line with an early TS because upon comparison to typical C=C and C-C bond lengths, the former is resembled to a much greater extent in the transition state. Further evidence of this comes from PES studies at the B3YLP/6-31G(d,p) level of theory, where equalization of bonds to 2.268 Å was achieved across the reactant frameworks.

Upon comparison with various other computational levels of theory, such as Becke3LYP/6-31G*, RHF/6-31G and LDF/DZV, which yielded lengths for the newly forming σ-bonds in the range 2.101-2.411Å, it can be concluded that semi-empirical/AM1 parametrization does not lead to any significant inaccuracy vs. 'ab-into' methods. In addition to this studies have shown that the HF level of theory predicts the key concerted C=C bonds of the transition state to be too short and methods based on DFT such as RB still yield significant errors for the transition state. More importantly the study found that DFT predicts C-C bonds which are too short, but C=C bonds in relative agreement with experiential values.. The general performance of NDDO methods perform to a high degree of accuracy when it comes to predicting bond lengths for molecules containing non-second row elements. Dewar, Jie, and Yu (1993) evaluated AM1 for 344 bond lengths yielding a very small unassigned error of 0.027Å. In addition to this because DFT methods have been found to be in relative agreement with experiment and AM1 calculated values are very similar, it can be concluded that the AM1 level of theory performs to a reasonable extent predicting geometries in a prototypical Diels-Alder reaction.

(As you say later on, AM1 performs very well for the systems that it was parameterised for. It fails spectacularly for systems that it hasn't Tam10 (talk) 11:35, 11 March 2016 (UTC))

In addition to these geometric studies the activation energies at 298.15K were calculated for both the semi-empirical/AM1 and DFT levels of theory seen below.

	Semi-empirical/AM1			B3LYP/6-31G*
	Absolute energy (Hartrees)	Sum of electronic and thermal energies at 298K (Hartrees)	Activation energy (kcal/mol)	Absolute energy (Hartrees)	Sum of electronic and thermal energies at 298K (Hartrees)	Activation energy (kcal/mol)
Diels-Alder TS	0.11165479	0.259453	25.4944604	-234.54114007	-234.394276	20.7498602
Ethylene	0.02619028	0.080252	-	-78.59380796	-78.539646	-
Cis-butene	0.04879719	0.138573	-	-155.99549125	-155.906505	-

It is clear that the DFT level of theory predicts a substantially lower activation energy. However experimental literature values of the activation are 27.5±2 kcal/mol meaning the AM1 level of theory predicts more accurate values of the activation energy in this reaction. This difference can be attributed to the way each method calculates thermodynamic properties. AM1 does this by parametrization of results against a database of experimental data such that its accuracy is data-base dependent. In this case this could have introduced a bias making final values more accurate. In contrast to this DFT is the higher level of theory based on an ab-initio framework, it is found for this reaction that during the TS, an open-shell system, a level of spin-contamination can cause deviations from ideal results. This is due to the use of basis set Kohn-Sham orbitals used to obtain orbital densities from which energies are then derived. However in the TS it is the density, not the individual orbitals that are key and as such the wave-function used is incorrect To conclude semi-empirical/AM1 theory bypasses these errors by parametrization, such that in this case it yields results in agreement with literature.

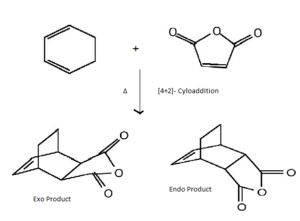
Regioselective Diels-Alder cycloaddition of cyclohexa-1,3-diene and maleic anhydride

The Diels-Alder reaction between cyclohexa-1,3-diene and maleic anhydride will now be analysed in order to identify the determine factors influencing stereoselectivty preferences for endo/exo transition states. Even to this day the determinants of this had remained controversial with dispersion, sterics and secondary orbital interactions all seen to be factors. The product of the reaction will be determined by this; endo(/exo)-bicyclo[2.2.2]oct-5-ene-2,3-dicarboxylic anhydride. This remains one of the most challenging sterochemical results to analyse conclusively and results in the endo-rule for Diels-Alder reactions and is most prevelant when the dieneophile bears α- electron withdrawing groups (EWG's).

Optimization of maleic anhydride

As for the prototypical Diels-Alder reaction between cis-butene and ethylene, both reactant species are first optimized at the semi-empirical/AM1 level of theory such that they can be subsequently used in to produce a guess transition state structure to be optimized via TS(Berny). Below are the results for the optimized maleic anhydride reactant.

Jmol Structure	Energy (Hartrees)	Point Group
	-0.12182385	C2v

Using the .chk file the HOMO and LUMO are visualized below;

Maleic anhydride: HOMO MO	Maleic anhydride: LUMO MO
HOMO MO: optimized maleic anhydride is symmetrical with respect to the plane	LUMO MO: optimized maleic anhydride is antisymmetric with respect to the plane

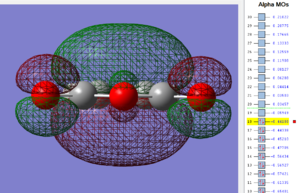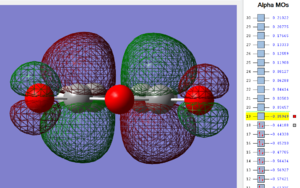Optimization of cyclohexa-1,3-diene

Similarly, results for the semi-empirical/AM1 optimized structure for cyclohexa-1,3-diene are shown below.

Jmol Structure	Energy (Hartrees)	Point Group
	0.02771128	C2

Again, the HOMO and LUMO are visualized below;

cyclohexa-1,3-diene: HOMO MO	cyclohexa-1,3-diene: LUMO MO
HOMO MO: optimized cyclohexa-1,3-diene is antisymmetric with respect to the plane	LUMO MO: optimized cyclohexa-1,3-diene is symmetric with respect to the plane

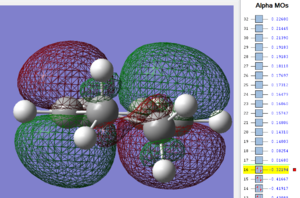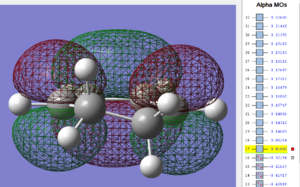Optimising the exo and endo transition structures

To produce a TS(Berny) guess input structure the optimized cyclohexa-1,3-diene and maleic anhydride reactants were positioned in relative orientations corresponding to exo and endo transition states. For endo this required positioned maleic anhydride co-planar to cyclohexa-1,3-diene, but crucially the electron-withdrawing carbonyl substituents of the diene are under the diene unit, below the position of the developing diene unit π-bond. In contrast the exo transition state guess required the electron-withdrawing diene units to be positioned in an anti-orientation, above the diene plane. The results of each successful optimization are shown below.

Transition state structure	Optimization Method	Energy (hartrees)	Relative energy (kcal/mol)	Visualized Im-frequency (cm-1)
Exo- Diels-Alder 1,3-cyclohexadiene and maleic anhydride	Semi-empirical/AM1	-0.05041984	0.06808228	Exo imaginary frequency at -812.15cm-1
Endo- Diels-Alder 1,3-cyclohexadiene and maleic anhydride	Semi-empirical/AM1	-0.05150480	0.00	Endo imaginary frequency at -806.41cm-1

The presence of a single imaginary frequency confirmed that the transition states for both optimizations had been achieved. The corresponding frequencies for the endo and exo are -806.41/-812.15cm^-1. Both transition states are similar to that seen for the prototypical Diels-Alder reaction, whereby the terminal carbon reaction centers involved in forming new σ-bonds vibrate synchronously in the manner expected for a concerted transition state during bond formation. As discussed before this single imaginary frequency and corresponds to the only vibrational mode in the system that will lead to a reaction. It is seen that the relative energies of the transition state structures and the magnitude of the imaginary frequency are correlated. The exo transition state is approximately 0.06808 kcal/mol higher in energy than its endo counterpart and has an imaginary frequency 5.74 wave-numbers more negative. These results tell us that the exo transition state is higher in energy and therefore to subsequently react via the vibration corresponding to the imaginary frequency requires a larger force-constant, owing to the harmonic approximation used in the calculations.

Comparison of the endo and exo transition state structures

In order to grasp the full nature of the endo TS stability, full analysis of both transition state geometries, visualization of key MO overlaps and relative activation energies is required.

• 
  Figure 13: Exo transition state atomic labels
• 
  Figure 14: Endo transition state atomic labels

Table 12. Endo and Exo Gometry Comparison

Atom Labels	Exo TS-Bond Lengths (Å)	Endo TS-Bond Lengths (Å)
C1-C4	1.39677	1.39725
C1-C2	1.39438	1.39305
C2-C7	1.48976	1.49053
C7-C10	1.52210	1.52296
C3-C15	2.17026	2.16239
C2-C17	2.17059	2.16237
C15-C17	1.41011	1.40849

[Note all bond distances obtained using Gaussview direct inter-nuclear measurements. These values are as such inherently inaccurate and confidence can only be given to two decimal places]

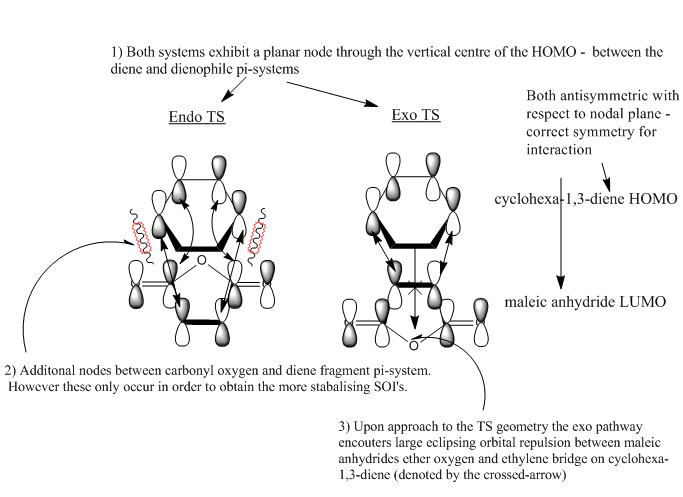
The first key geometric difference between the two transition states is the length of the forming/breaking bonds between C2-C17/C3-15 - in the exo transition state these are larger than the equivalent distance in the endo structure. The largest magnitude of this difference was 0.00822Å, notice that the two bond lengths are slightly different in both TS's inferring a small degree of asynchronicity in the reaction mechanism, however this could be due to inherent inaccuracies associated with AM1 optimizations. More importantly is the fact that this distance is proportional to the extent of the primary orbital interactions in the HOMO and LUMO of both transition states. The greater overlap interactions confer the extent to which the endo pathway is preferred. The imaginary frequency was seen to be less negative for the endo TS suggesting that the force needed to overcome steric repulsion and obtain optimum overlap of the diene and dienophile π systems required less energy. The current reasoning for this, as laid down by Woodward and Hoffmann is that of an additional interaction in the endo TS between the lower lobe of the π-orbital of diene and the upper lobe on the carbonyl carbon p-orbital lobe of the dienophile. These are known as secondary orbital interactions (SOI's), and do not lead to a bond (these are quantified in the next sub-section). From the relative endo and exo C4-C20 interatomic distances, 2.89 and 3.78Å respectively, and the fact that in the exo TS the SOI bonds are in an anti-arrangement, only the endo TS observes any significant SOI TS stabilization. However both of these distances are large for efficient overlap to occur.

(This slight distortion of symmetry is probably due to the threshold that Gaussian considered it converged. A tighter threshold and a better grid will yield a more symmetric result, but these values are pretty meaningless Tam10 (talk) 11:35, 11 March 2016 (UTC))

Both transition states steric repulsions can be mainly attributed to inter-spatial interactions between the diene -CH2CH2- fragment and dienophile O=C-O-C=O fragment. Examining the endo TS inter-fragment distance = 3.89Å, in contrast the exo TS = 2.98Å, this accounts for a percentage difference of 23.1%. To quantify the extent of steric repulsion, we refer back to the literature value of carbon atom Van der Waals radii, 1.77Å. It is immediately clear that for the exo transition state the two carbon atoms come within a distance smaller than the sum of their Van der Waals radii leading to large steric repulsions which do not occur in the endo TS. This prevents the exo TS from obtaining as much of the favourable orbital overlap (primary) as the endo TS. Counter to this argument other studies have postulated that it is in fact the endo-pathway actually proceeds through a more stericaly hindered transition state, but that this is only so that maximum SOI's are obtained.

Further to this argument of endo-preference, solvation studies as outlined in Ian Fleming's book 'Frontier Orbitals and Organic Chemical Reactions', tells us that electrostatic effects lead to a destabilization of the exo TS. Since H-C bonds are polarized towards the carbon, the methylene groups and the carbonyl carbons in maleic anhydride will repel each other. Further to this, dispersion interactions through π-π contacts in the endo TS have also been put forward, due to a lack of Mulliken charge transfer occurring during the TS[32].

Lastly from comparing the partially broken C1-C4 π-bond length in the cyclohexa-1,3-diene fragment is seen that in the exo TS = 1.39677Å this bond is shorter than the corresponding bond in the endo TS = 1.39725Å. This provides evidence that the exo TS is 'earlier' as it resembles the reactants more than the products.

Endo and Exo Transition state primary and secondary orbital overlaps

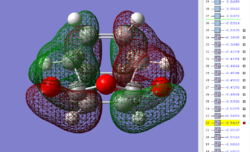
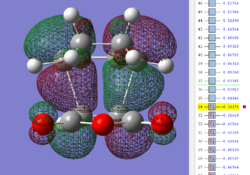
Key evidence: the identification of primary orbital overlap (POI) for both the exo and endo transition states in the HOMO and LUMO, and subsequent verification of possible SOI's. Note that both the HOMO and LUMO of both transition state structures are anti-symmetrical with respect to the central C-C plane.

Endo TS: HOMO MO	Endo TS: LUMO MO	Endo TS: HOMO-12 MO	Endo TS: HOMO-15 MO
		Secondary π overlap identified	Secondary π overlap identified

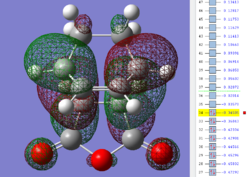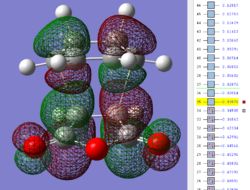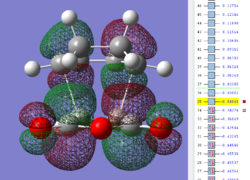
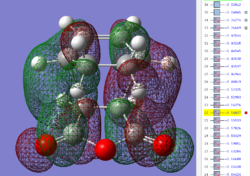
Exo TS: HOMO MO	Exo TS: LUMO MO	Exo TS: HOMO-12 MO	Exo TS: HOMO-15 MO
		Secondary π overlap identified minimal	Secondary π overlap identified not present

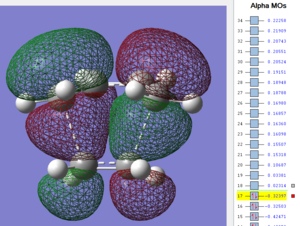
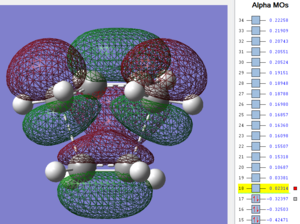
Firstly, as expected from the imaginary frequencies, primary orbital overlap exists for both the endo and exo TS's between the HOMO of cyclohexa-1,3-diene and LUMO of maleic anhydride in accordance with normal electron transfer. Secondary orbital overlap has been mentioned previously, however a more concise description from Ian Flemmings 'Frontier Orbitals in Organic Chemistry' is given - SOI's are frontier orbital interactions only present in pericyclic reactions that are not involved in the formation of new bonds (and are seen in the FO's). For the cycloaddition between maleic anhydride and cylcohexa-1,3-diene this should occur on both sides of the p-orbital lobes of the developing π-bond in the diene and the p-orbital lobes of the carbonyl carbons in the dienophile. The overlap for in this particular cycloaddition is in-phase and therefore a favourable 'bonding' interaction. It must be noted that this is not always the case, for example in the cycloaddition of cyclopentadiene and tropone the FO SOI is anti-bonding leading to exo TS favourability.

As can be seen for both the endo and exo TS's the p-orbitals on the oxygen atoms are non-interacting and do not contribute to any stabilization. It can be seen in the exo TS HOMO that the developing π-bond is isolated at the back of the molecule because it is too spatially removed/has negligible integral overlap with any suitable orbitals on maleic anhydride. This is not the case in the endo TS. These interactions are visualized and it is seen that an endo orientation of the diene and dienophile components is required for this overlap to occur.

Both POI's and SOI's are visualized in the figures below, furthermore some explanation is given as to the key overlaps where the nodal properties of the HOMO between the -(C=O)-O-(C=O)- fragment and the remainder of the system can be analysed.

• 
  Figure 15: a) In-depth - Primary and secondary orbital interactions in the endo TS - POI (straight) & SOI (curved)

• 
  Figure 16: b) MO - Primary and secondary orbital interactions in the endo TS - POI (BLUE) & SOI (ORANGE)

(Good diagrams here to explain your paragraphs Tam10 (talk) 11:35, 11 March 2016 (UTC))

However secondary orbital overlap between the p-lobes of the terminal carbons in the developing π-bond in the diene and the carbonyl carbon p-orbital were also seen in orbitals below that of the endo and exo HOMO's. For more core-like MOs, in particular HOMO-12/15, the endo TS has further SOI's. Furthermore, in contrast conventional theory, some SOI was also identified in the exo TS, however these are minimal due to their relatively sparse-orientations. All of these orbitals are populated and hence this difference leads to the relative electronic stabilization of the endo TS. These interactions, in addition to conventional theory, act to further lower the electronic energy of endo TS alongside the necessary primary orbital overlap, which forms the two new σ-bonds.

IRC analysis

On performing the IRC for both the endo and exo transition states and optimizing the final product it is not clear as to whether the exo-product is lower in energy (convention) than the endo product. However the IRC does gives us more insight into the physical factors controlling the barrier heights. In both cases in the early stages of the process, the system energy, ΔE, monotonically becomes more and more destabilized as the reactants approach each other along the reaction coordinate and is a result of the onset of overlap and Pauli repulsion between occupied π orbitals of the diene and dienophile. It is then expected that within the primary and secondary overlap between the corresponding π-densities that becomes stabilizing. At this point along the RC, all the remaining energy of activation purely stems from the degree of deformation/strain energy to obtain adequate orbital overlap for the symmetry-constricted pericylic reaction.

Earlier it was found that the exo TS was earlier, which leads to the counter-intuitive conclusion the deformation energy in the exo pathway is larger yet the TS is reached earlier. However this is explained through the use of TS geometries seen previously - inter-spatial interactions between the diene -CH2CH2- fragment and dienophile O=C-O-C=O fragment. To avoid an extreme increase in Pauli repulsion between eclipsed -CH2CH2- fragment sp³ hydrogen bonding orbitals and the ether O lone-pair orbital, which can be visualized in the FO's of both the exo and endo TS's in the previous section, the bridging unit has to bend away significantly from the oxygen atoms. This was quantified by calculating the difference in the change in dihedral angle between C15-C3-C2-C7 across the bonding between the diene and dienophile for the two TS's to their corresponding products. Studies have shown that this correlates with activation barrier height and is related to the deformation energy/sterics in the TS's. A positive value of Δ(Δd) corresponds to a stericaly more hindered exo TS as a measure of the extent of rotation of the pseudo-plane of the incipient dienophile to obtain the TS geometry.

	Endo TS - Product Δd (°)	Exo TS - Product Δd (°)	Δ(Δd) (°)
Semi-empirical/AM1	21.83057	22.97217	1.1416

Transition state	Number of Steps	IRC Path	Jmol Exo/Endo Final Products	Final Product Relative energy (kcal/mol)	Point group
Exo	20	IRC path evaluated at 20 points in both directions		0.15123	C1
Endo	20	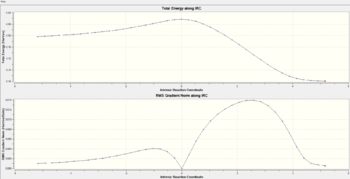IRC path evaluated at 20 points in both directions		0.00	C1

Note: As the IRC's are not fully converged because as the RMS gradient levels out, further optimization takes ever more computational time. To bypass this constraint the final intermediate IRC structures for the exo and endo structures were subsequently optimized, as seen in the next section, of which the results are shown in the final product column in the table above, with a relative exo product energy 0.15123kcal/mol above that of the endo product.

Activation energies

In this section the energies of the reactants, products and transition states are tabulated and the activation energies at 0K and 298.15K calculated at both the semi-empirical/AM1 and DFT levels of theory. Factors that influence activation energy discussed in the sections proceeding this are used to explain the results and new factors influencing the relative product energies are introduced and the results are then compared to experimental values.

Tabulated Energies for the components for the cycloaddition of cyclohexa-1,3-diene and maleic anhydride, at AM1 and DFT levels of theory

	Semi-empirical/AM1			B3LYP/6-31G*
	Absolute energy (Hartrees)	Sum of electronic and zero-point energies (Hartrees)	Sum of electronic and thermal energies at 298K (Hartrees)	Absolute energy (Hartrees)	Sum of electronic and zero-point energies (Hartrees)	Sum of electronic and thermal energies at 298K (Hartrees)
Exo-Diels-Alder TS	-0.05041984	0.134880	0.144881	-612.6793354	-612.498007	-612.487670
Endo-Diels-Alder TS	-0.05150480	0.133494	0.143683	-612.68339566	-612.502208	-612.491836
Exo-Diels-Alder Product	-0.15990926	0.031703	0.040681	-612.75577814	-612.569427	-612.560016
Endo-Diels-Alder Product	-0.16017053	0.031462	0.040459	-612.75830997	-612.572076	-612.562625
1,3-cyclohexadiene	0.02771128	0.152502	0.157726	-233.41891276	-233.296117	-233.290939
maleic anhydride	-0.12182385	-0.063350	-0.058197	-379.28953521	-379.233652	-379.228469

[See Appendix for DFT .LOG files]

Using the results from this table the activation energies for the reaction at 0K and 298.15K are calculated in the table below

Tabulated activation Energies for the cycloaddition of cyclohexa-1,3-diene and maleic anhydride at 0K and 298.15K - at AM1 and DFT levels of theory

	Semi-empirical/AM1		B3LYP/6-31G*
	Activation energy at 0K (kcal/mol)	Activation energy at 298K (kcal/mol)	Activation energy at 0K (kcal/mol)	Activation energy at 298K (kcal/mol)
Exo-Diels-Alder TS	28.6947594	28.4588157	19.9309602	19.9158999
Endo-Diels-Alder TS	27.825031	27.7070592	17.2947923	17.2696919

When compared to the experimental value of 11.4kcal/mol (carried out in dichloromethane solvent) it is clear that the DFT level of theory produced far more accurate results than the AM1 method. Both levels of theory are not complete and both neglect certain real effects of the cycloaddition reaction, some of which I have documented below.

Semi-empirical/AM1 neglected factors

AM1 being an inherently semi-empirical method has the main obvious drawback of not fully modelling a basis set unlike at the DFT level of theory. However unlike early theories such as MNDO and MNDO/3, it utilises the NDDO approximation which does at least relate the calculations to an actual basis set. This does however raise the number of two-electron two-center integrals in the calculations by a factor of 100 for each pair of atoms containing an (s,p) basis.

In addition to this many other neglected factors have been documented. Firstly AM1 can predict some excessive repulsion terms at Van der Waals distances in sterically crowded molecules which could have led to the exo TS being unfavourably destabilised in this report. Moreover with respect to the energetics associated with conformational changes and reactions, the AM1 level of theory does not fully account for electron-correlation energy as it is only introduced by parametrization of semi-empirical HF equations. Because these energies tend to be more important in TS structures than in minima, activation energies are likely to be too high. Secondly semi-empirical methods are unreliable when it comes to predicting weak intermolecular interactions such as London dispersion forces(an electron correlation phenomenon) which were found in literature to play a role in endo TS stability. Finally, energetic barriers to rotation about bonds having partial bond character tend to be significantly low at semi-empirical levels. This was found to be important for the Diels-Alder deformational contribution to the activation energy, Cramer's 'Essentials of Computational Chemistry' backs this up as it observes errors for rotation about C-C bonds in conjugated systems are significant. Computational literature tests have shown the average geometrical errors in bond lengths and dihedral angles to be 0.05Å and 12.5° respectively.

DFT neglected factors

DFT primarily neglects the distribution of electron density in the second, non-prototypical, Diels-Alder cycloaddition because of the involvement of hetero-atoms for the cyclohexa-1,3-diene/maleic anhydride system studied in this report. This is backed up in literature where even ab-initio methods with much larger basis sets produce data that deviates significantly from experimental values in the gas phase and when solvated. In addition DFT tends to overestimate polarities of charge transfer complexes, like the Diels-Alder exo and endo transition states, this leads to systems that are too tightly bound. Another weakness of DFT is that it tends to over-delocalize structures which can show up in geometrical predictions. Thus, for instance, in butadiene DFT predicts the formal single bond to be too short and the formal double bonds to be somewhat too long. However overall accuracies in bond lengths is about 0.001Å. Finally DFT frontier orbtials were double-checked in order to verify AM1's results as these are key orbitals in the cycloaddition reaction, seen in the figures below.

Endo TS: DFT - Endo HOMO	Endo TS: DFT - Endo LUMO	Exo TS: DFT - Exo HOMO	Exo TS: DFT - Exo LUMO

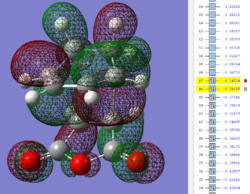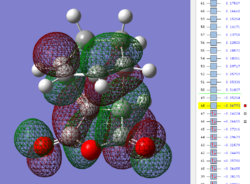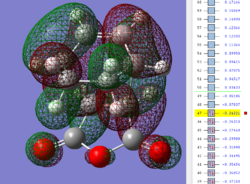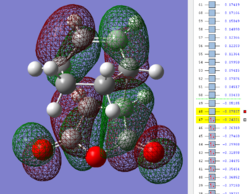It is immediately evident from the HOMO and LUMO visualizations that the DFT theory has not followed conventional theory in the regard that both TS HOMO's is not the in-phase overlap of the diene HOMO and dienophile LUMO and out-of-phase overlap in the TS LUMO's. This level of theory shows these key POI are very similar to the ones seen from the AM1 calculations. It is therefore concluded that AM1 produces reliable results even though it does not specifically take into account a full basis set like the DFT ab-initio method. See below for a diagramatic representation of the expected FO overlaps.

Figure 17; Expected FO overlaps for the Diels-Alder cycloaddition

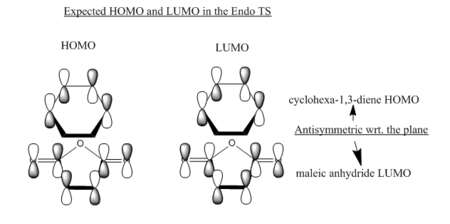
However most importantly, these results provide qualitative evidence that the endo TS is lower in energy than the exo TS and is therefore the kinetic product of this reaction. This may or may not be for the steric and SOI reasons discussed in previous sections, but evidence was gathered for those hypotheses. Transition states for the DFT calculations are confirmed by the presence of a single imaginary frequency for the endo and exo structures - these are -446.73cm^-1 and -448.42cm^-1.

In addition it is seen that the endo product is lower in energy relative to the exo product. The relative energy of the exo product calculated at the AM1 level of theory was 0.151kcal/mol and at the DFT level of theory was 1.589kcal/mol. Generally this is the other way around, for example in the cycloaddition of cyclopentadiene and maleic anhydride, but in this case this is not so. This is due to the relative steric clashes observed in the products - in the exo product the -CH2CH2- bridge observes significant steric clashes with the maleic anhydride fragment whereas in the endo product this interaction is replaced by the less repulsive clashing between the new π-bond on the diene and the maleic anhydride fragment. Both of these interactions are visualized in the figure below. The result of these findings is that the endo product is both the kinetic and thermodynamic product.

• 
  Figure 18: Possible steric interactions leading to exo(A) and endo(B) product relative thermodynamic stabilities

Tabulated Key Steric Interactions in the endo and exo Diels-Alder products

Semi-empirical/AM1		B3LYP/6-31G* (DFT)
Exo product main steric interaction (Å)	Endo product main steric interaction (Å)	Exo product main steric interaction (Å)	Endo product main steric interaction (Å)
2.94250	2.98270	2.98433	2.98786

Recalling that the VDW radius of a carbon atom is 1.77Å, it is clear that both interactions are within 2x this value. As a result both are sterically significant, however the exo interaction is much shorter range and more repulsive. This difference leads to the exo product instability seen in the numerical energetic results.

Finally, as expected the activation barriers of both the endo and exo pathways for both levels of theory decreased as the system thermal energy increased, this is for the same reasons as discussed in the Cope rearrangement tutorial.

Conclusion

In this report both the mechanisms of the Cope Rearrangement and also prototypical and non-prototypical forms of Diels-Alder reaction were investigated using the Guassian 5.0 program.

In terms of the Cope rearrangement of 1,5-hexadiene it was found that the chair TS and gauche-3 ground state conformer were energetically favoured along the reaction pathway. Both the HF/3-21G and B3LYP/6-31G* levels of theory were utilized and it was found that the DFT and HF calculations both predicted accurate geometries, but crucially at the expense of increased computational time taking into account electron correlation, DFT more accurately predicted activation energies when compared to literature values. For the chair TS the TS(Berny) and frozen coordinate methods were used to locate the TS, both methods were then compared. Further to this parametrization QST2 method was used to optimize the boat TS, this rapidly cuts the computational time needed as transit-guided quasi-Newton proceed without full evaluation of second derivative matrices. QST3 was not invoked as this is more time-consuming to set up and unnecessary as the TS was already converged upon using QST2.

For the Diels-Alder reactions, both calculated at the semi-empirical/AM1 level of theory, the prototypical cycloadditon between but-1,3-diene and ethylene demonstrated the synchronous nature of bond formation, visualized in the single imaginary frequency which characterizes a transition state species. However the stereo-selective Diels-Alder reaction between cyclohexa-1,3-diene and maleic anhydride provided much more interesting information for the nature of the cycloaddition reaction pathways. Endo kinetic preference was shown firstly by its reduced sterics - through-space distances between the O=C-O-C=O fragment and the -CH2CH2- fragment were within 2xVDW radii of the two fragments in the exo TS but not in the endo TS. Further to this energetically stabilising secondary orbital effects were shown to be only present significantly in the endo TS further stabilizing it. The relative activation energies for the two pathways quantified these arguments with the endo TS being 0.164kcal/mol (AM1) lower in energy.

The most interesting result from the study however came from the relative energies of the endo and exo pathway products. It was found that the endo product was 1.589kcal/mol (DFT) more stable. For most reactions this is the other way around, however in this case larger specific steric interactions only seen in the exo product leading to the endo preference. This leads to the conclusion that the endo product is both the kinetic and thermodynamic product. Finally, these results were compared to the DFT level of theory and it was found that activation energies were more in agreement with experimental values, the limitations of both levels of theory were discussed, of which may have led to these deviations in values. However crucially it was found that AM1 produced FO's resulting from key POI's in agreement with the DFT ab-initio method and therefore further studies of the system would be carried out at this semi-empirical level of theory to save on computational time. Further study with theoretical nuclear-independent chemical shifts (NICS's) which are able to quantify aromaticity and therefore electron delocalization, of which would only occur if SOI's were present in the TS's. Many factors could possibly be determining endo-stereoselectivity however such a study would conclusively show that SOI's play a prominent role.

Appendix

Non-prototypical Diels-Alder DFT .LOG files

File	Log file source
Maleic anhydride	File:PSRWMALEICB3YLP.LOG
cylcohexa-1,3-dine	File:PSRWCYCLOHEXAB3LYP.LOG
Endo TS	File:PSRWENDOTSB3LYP.LOG
Exo TS	File:PSRWEXOTSB3LYP.LOG
Endo Product	File:PSRWENDOPRODUCTB3LYP.LOG
Exo Product	File:PSRWEXOPRODUCTB3LYP.LOG