Rep:Mod:Testpage
Mod:phys3
In this experiment,Cope Rearrangement reaction is given as a tutorial, which is followed by an exercise to obtain a transition structure for Diels Alder reaction between butadiene and ethylene. At the end of this computational lab, by using MO diagrams of HOMO and LUMO, study of regioselectivity is carried out, which demonstrates endo selectivity of reaction between cyclohexa-1,3-diene and maleic anhydride, using "secondary orbital overlap effect".
Cope Rearrangement Tutorial
Introduction
The Cope rearrangement is an extensively studied reaction involving the [3,3]-sigmatropic rearrangement of 1,5-dienes. In this tutorial, different methods were used to approach real TS structure and to determine reaction paths theoretically.
This tutorial can be summarized into several parts:
Part 1 Optimization of the reactant 1,5-hexadiene using different methods.
Part 2 Getting right transition structures of Cope Rearrangement.
Part3 Using results of part 1 and part 2 to calculate corresponding activation energies of both the chair and boat TS paths.
1,5-hexadiene optimization
a)Drawed a molecule of 1,5-hexadiene with an anti linkage for the central four carbon atoms and then optimized it using method HF/3-21G.(anti1)
b)Drawed a molecule of 1,5-hexadiene with an 'gauche' linkage for the central four carbon atoms and then optimized it using method HF/3-21G.(gauche1)
e)Drawed a molecule of 1,5-hexadiene with an anti linkage for the central four carbon atoms and then optimized it using method HF/3-21G.(Ci anti2)
f)Reoptimised Ci anti2 at B3LYP/6-31G(d) level.(Ci anti2)
| Conformer | Structure | Point Group | optimization method | Energy/Hartrees | Dicussion | |||
| anti1 |
|
C2 | HF/3-21G | -231.69260 | Compared it to anti1 in Appendix 1,matches well. | |||
| gauche1 |
|
C1 | HF/3-21G | -231.69266 | Result matches well with gauche3 in Appendix 1. | |||
| Ci anti2 |
|
Ci | HF/3-21G | -231.69254 | Result matches well with anti2 in Appendix 1. | |||
| Ci anti2 |
|
Ci | B3LYP/6-31gd | -234.61171 | Compared to the lower level theory result above, energy of this reoptimized molecule is lower without obvious overall geometry change. |
g)Discussion of the results obtained by using B3LYP/6-31G(d)
Obtained vibration frequencies from the Frequency calculation, it can be seen that all frequencies are positive. Frequency calculation actually is the derivative of potential energy surface and a negative frequency always indicates a transition state. SO this frequency calculation makes sure that obtained optimized structure is stable at least.
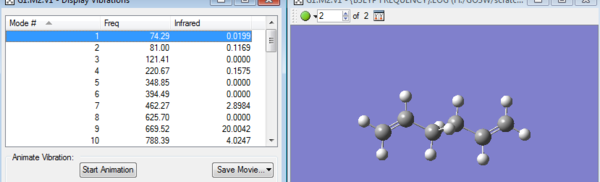
| Term | Energy Value | Description |
| Sum of electronic and zero-point Energies | -234.469203 | potential energy at 0K including zero-point vibrational energy |
| Sum of electronic and thermal Energies | -234.461857 | E(298.15 K and 1 atm)+Evib + Erota +Etrans |
| Sum of electronic and thermal Enthalpies | 234.460913 | [H = E+RT] |
| Sum of electronic and thermal Free Energies | -234.500777 | [G = H-TS] |
Optimizing the "chair" and "Boat" Transition Structures
a) Drawed an allyl fragment and optimized it using the HF/3-21G level of theory, then using optimized allyl fragment to construct a guess structure of chair transition state.
b) Optimized the guess chair TS structure on HF/3-21G level method to TS(berny). (Chair TS 1)
c)and d)Optimized the guess chair TS structure using HF/3-21G level method to TS(berny) after the frozen coordinate method. (Chair TS red)
e) Used optimized Ci anti2 molecule as both the reactant and the proudct as this reaction is rearrangement, with labeled atoms corresponding to each other. (Picture 1) Set up QST2 calculation and wrong transition state structure came out as a failed result.
Modified original reactant and product geometries to be closer to the boat transition structure. Set up QST2 calculation again.(QST22)
f) Used optimized chair transition structures to run Intrinsic Reaction Coordinate(IRC) method and then took last point on the IRC to run a normal minimization, which energy is shown below as 'product from IRC'.
Used optimized boat transition state from QST22 to run IRC method and then took last point on it to run a normal minimization, which energy is shown below as 'gauche 3'. Also, data of the starting material of the boat transition state calculation is given as 'anti2' as comparison.
Also,activation energy calculation is present below, which is calculated using Eproduct - ETS
Results and Discusstion
Chair TS
| Name | Structure | Energy/Hartrees HF/3-21G |
breaking bond length/Å |
| Chair TS 1 | -231.61932 | 2.02045 and 2.02064 | |
| Chair TS red | -231.61932 | 2.02062 and 2.02055 |
Discussion
As can be seen, breaking bond lengths obtained using different medthods are similar.
Boat TS
Activation energy calculation
Summary of energies (in hartree)
| HF/3-21G | B3LYP/6-31G* | |||||
|---|---|---|---|---|---|---|
| Electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | Electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | |
| at 0 K | at 298.15 K | at 0 K | at 298.15 K | |||
| Chair TS | -231.619322 | -231.466702 | -231.461343 | -234.556983 | -234.414929 | -234.409009 |
| product from IRC | -231.691667 | -231.538704 | -231.531794 | -234.610708 | -234.468205 | -234.460939 |
| Boat TS | -231.602802 | -231.450929 | -231.445300 | -234.543093 | -234.402342 | -234.396008 |
| Reactant (anti2) | -231.692535 | -231.539539 | -231.532566 | -234.611710 | -234.469203 | -234.461856 |
| product (gauche3) | -231.692661 | -231.539485 | -231.532646 | -234.611329 | -234.468693 | -234.461464 |
*1 hartree = 627.509 kcal/mol
Summary of activation energies (in kcal/mol)
| HF/3-21G | HF/3-21G | B3LYP/6-31G* | B3LYP/6-31G* | Expt. | |
| at 0 K | at 298.15 K | at 0 K | at 298.15 K | at 0 K | |
| ΔE (Chair) | 45.18 | 44.21 | 33.83 | 32.60 | 33.5 ± 0.5 |
| ΔE (Boat) | 55.57 | 54.81 | 41.64 | 41.07 | 44.7 ± 2.0 |
Discussion
No matter which methods used, activation energy of reaction path via Chair TS is lower than the boat one, which means this Cope Rearrangement preferentially processes via chair transition state if it is kinetically controlled. Another important thing should be noticed is that results obtained using B3LYP method are closer to the experiment data apparently, which can be explained by higher level theory behind B3LYP method.
Exercise Part 1
Introduction
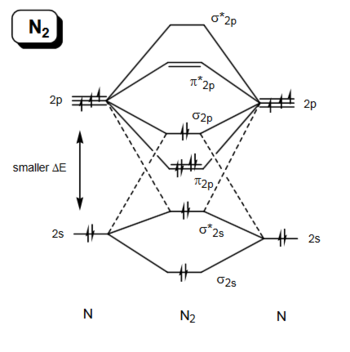
In the process of cycloaddition, HOMO of one fragment interacts with the LUMO of the other reactant to form two new σ bonds if the orbitals have same symmetry to overlap significantly. This requires interacting orbitals have same symmetry,e.g. asymmetric HOMO interacts with asymmetric LUMO to form an asymmetric transition state orbital,same as symmetric case.
cis butadiene
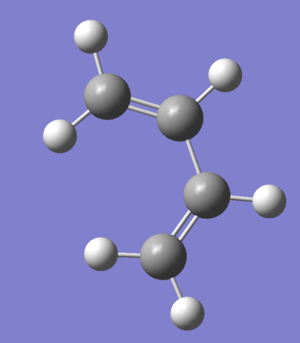
| orbital | orbital shape | symmetry(with respect to plane) | Energy/Hartrees Semi/AM1 |
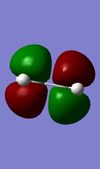
| HOMO | antisymmetric(a) | -0.34381 | |
| LUMO | symmetrix(s) | 0.01707 |
ethylene
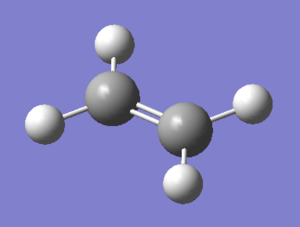
| orbital | orbital shape | symmetry(with respect to plane) | Energy/Hartrees Semi/AM1 |
| HOMO | symmetric(s) | -0.38777 | |
| LUMO | antisymmetric(a) | 0.05284 |
butadiene and ethylene reaction
To guess transition state structure for this Diels Alder reaction,used several different methods and then compared results to determine the TS structure.
a)TS QST2(Semi-AM1)
b)TS QST2(HF/3-21g)
c)TS QST2(B3LYP/6-31G(d))
d)Guess TS and then optimised it to TS(Berny) (HF/3-21g)and
e)(B3LYP/6-31G(d))
f)frozen coordinate method (HF/3-21g)
g)f)frozen coordinate method (B3LYP/6-31G(d))
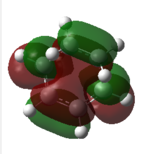
| method | forming bond length | LUMO | HOMO | degenerate)HOMO | Energy of LUMO/HOMO |
| a | 2.11921 / 2.11932 | 0.02316
-0.32395 -0.32499 | |||
| b | 2.21071 /2.20855 | 0.14241
-0.30086 -0.30294 | |||
| c | 2.27021/2.27474 | -0.00863
-0.21893 -0.22110 | |||
| d | 2.20979/2.20934 | 0.14241
-0.30088 -0.30292 | |||
| e | 2.27236/2.27238 | -0.00861
-0.21895 -0.22107 | |||
| f | 2.20969/2.21137 | similar as above | similar as above | similar as above | |
| g | 2.27235/2.27255 | similar as above | similar as above | similar as above |
Discussion of data
a) Energy difference between HOMO(ethylene)/LUMO(butadiene),which is symmetric interaction(s), is 0.40481 using Semi-AM1 method. Energy difference between HOMO(butadiene)/LUMO(ethylene),considered as asymmetric interaction(a), is 0.39381. Energy differences of these two ways is similar, which indicates that both MO interaction are possible,leading to degenerate TS molecular orbitals.
Also, from the TS orbitals diagrams obtained by different methods shown above,it can be seen that,although energies of orbitals are different due to different methods based on, all methods deduce similar degenerate HOMOs, one of which is symmetric with respect to plane while the other one is asymmetric.
From the orbital diagrams of the forming bond, it suggests the asymmetric interaction overpowers the symmetric one because the symmetric interaction produces a HOMO of TS which has inverse phases lobes on the forming bond,making significant overlap to form a bond is difficult.
b) Breaking bond lengths differ from one method to the other due to varied methods of different levels, but are not significant differences. Typical bond lengths of sp3 C-C bond is 154pm while 147pm for sp2 C=C bond.1,2 Van der Waals radius of carbon atom is 170pm. So the bond length of forming σ bonds is longer than C-C single bond but shorter than 2*170 pm, which indicates the existence of attractive interaction between end-carbons but are not bonds yet.
c)

The only one negative frequency corresponds to transition state of reaction and the forming process is synchronous, which is shown clearly on the animation. Compared to negative frequency, positive frequency do not correspond to transition state any more.
Exercise part 2
Introduction
a) If the dieneophile has substituents, which have π orbitals that can have significant overlap with new forming double bond, reaction involving it presents regioselectivity and stereoselectivity. Cyclohexa-1,3-diene undergoes facile reaction with maleic anhydride to give the endo adduct, which has transition state with lower energy but also product with higher steric repulsions, which suggests this reaction should be under kinetic control.3
b)"secondary orbital overlap effect" in this reaction can be described as stabilization of endo TS by π orbital overlap of the C=O group with the diene HOMO.
Results and Discussion
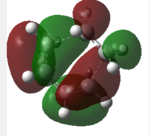
| Stereoselectivity | Energy | HOMO orbital shape | HOMO Energy/Hartrees Semi/AM1 |
discussion |
| exo | -0.05041959 | -0.34275 | carbonyl group does not involve in bond forming interaction(orbital overlap),which leads to unstable TS. | |
| endo | -0.05150478 | -0.34505 | Carbon of carbonyl group involves in orbital overlap ("secondary orbital overlap effect"),giving out a more stable TS. |
| Stereoselectivity | Image | distances | discussions |
| exo | 2.94515/2.94394 | distances between these closest groups are longer than the endo one, which leads to less steric repulsion and hence thermodynamically more stable TS and adduct. | |
| endo | 2.89239/2.89208 | Endo transition structure and adduct is more sterically congested due to shorter distances, thus thermodynamically less stable. |
b)In these computational calculations, condition under which the reaction actually being carried out is not considered. In real experiment, temperature and solvents used may turn the kinetically controlled product to thermodynamically controlled product, which means the reaction path also changes.
Conclusion
Computational simulation gives idea of transition state structures and related energies, which can then be applied to determine reaction paths and also to explain stereoselectivity of a reaction. Qualitatively,compared to experimental data, computational results are reasonable and useful.
References
1.Jump up^ Fox, Marye Anne; Whitesell, James K. (1995). Organische Chemie: Grundlagen, Mechanismen, Bioorganische Anwendungen. Springer. ISBN 978-3-86025-249-9.
2.Jump up^ Prof Chao-Jun Li, Ph.D. in lecture, March 2009 (needs citation)