Rep:Mod:Td81121

BH₃ molecule Optimisation

The molecule BH₃ was optimised using two different basis: 3-21G and 6-31G(d,p). Thereafter, the energy values obtained from both methods were compared.

3-21G Basis Set

[BH₃ 3-21G optimisation log file]

Summary Table
Property	Value
File Name	TC_bh3_opt
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	3-21G
Charge	0
Spin	Singlet
Energy	-26.46226429 a.u.
RMS Gradient Norm	0.00008851 a.u.
Dipole Moment	0.00 D
Point Group	CS
Computational Time	32.5 sec

Item               Value     Threshold  Converged?
 Maximum Force            0.000220     0.000450     YES
 RMS     Force            0.000106     0.000300     YES
 Maximum Displacement     0.000709     0.001800     YES
 RMS     Displacement     0.000447     0.001200     YES
 Predicted change in Energy=-1.672479D-07
 Optimization completed.

6-31G Basis Set

[BH3 - 6-31G(d,p) optimisation log file]

Property	Value
File Name	TC_bh3_opt_631g_dp
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
Spin	Singlet
Energy	-26.61532358 a.u.
RMS Gradient Norm	0.00008207 a.u.
Dipole Moment	0.00 D
Point Group	CS
Computational Time	4sec

Item               Value     Threshold  Converged?
 Maximum Force            0.000204     0.000450     YES
 RMS     Force            0.000099     0.000300     YES
 Maximum Displacement     0.000875     0.001800     YES
 RMS     Displacement     0.000418     0.001200     YES
 Predicted change in Energy=-1.452205D-07
 Optimization completed.

Property	Value
BH₃ optimised bond length	1.19 Å
BH₃ optimised H-B-H bond angle	120.0^o

The literature value for the BH bond length is quoted to be 1.190 Å. ^[1] The computed bond length is in good agreement with the literature value.

Total Energies

Method	Energy
3-21G	-26.46226429 a.u.
6-31G(d,p)	-26.61532358 a.u.

The calculated energies are different as different methods have been for the optimisation process. The 6-31G(d,p) incorporates more functions and so would give a better measure of the real energy value.

GaBr₃ Optimisation

The optimisation of GaBr₃ was carried out using a different basis set as the molecule has far larger electron density then the previous boron molecules. The chosen basis set was LanL2DZ, which sets the core electrons to an accurate constant (therefore modelled by a function called pseudo-potential) and performs optimisation on the valence electrons using the 6-31G basis set.

[GaBr₃ LanL2DZ optimisation D-space Link] [GaBr₃ LanL2DZ optimisation .Log file]

Property	Value
File Name	TC_gabr3_opt_LanL2Dz
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	LANL2DZ
Energy	-41.70082783.u.
RMS Gradient Norm	0.00000016 a.u.
Dipole Moment	0.00 D
Point Group	D3H

         Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000003     0.001800     YES
 RMS     Displacement     0.000002     0.001200     YES
 Predicted change in Energy=-1.282680D-12
 Optimization completed.

Property	Value
GaBr₃ optimised bond length	2.35 Å
GaBr₃ optimised Br-Ga-Br bond angle	120.0^o

Literature value - GaBr₃ bond length: 2.239A ^[2]. This is slightly different could perhaps be imporved by using a larger basis set.

BBr₃ Optimisation

In optimising the BBr₃ molecule, the basis set "GEN" with the keyword "pseudo=read gfinput" was utilised which allows the ability to specify pseudo potentials for individual atoms. The 6-31G(d,p) basis set was used for boron and LanL2DZ was used for the bromine atoms.

[BBr₃ GEN optimisation D-Space Link] [BBr₃ GEN optimisation .log file]

Summary Table
Property	Value
File Name	TC_bbr3_opt_GEN
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	GEN
Energy	-64.43645355 a.u.
RMS Gradient Norm	0.00001020 a.u.
Dipole Moment	0.00 D
Point Group	CS

Item Table

 Item               Value     Threshold  Converged?
 Maximum Force            0.000017     0.000450     YES
 RMS     Force            0.000010     0.000300     YES
 Maximum Displacement     0.000072     0.001800     YES
 RMS     Displacement     0.000043     0.001200     YES
 Predicted change in Energy=-1.759239D-09
 Optimization completed.

Property	Value
BBr₃ optimised bond length	1.93 Å
BBr₃ optimised Br-B-Br bond angle	120.0^o

Literature value: 1.903 Å^[3]. This reference value is in good agreement with the computed value and further enhances the reliability of the calculations.

Bond comparison of BH₃ BBr₃ and GaBr₃

Molecule	Bond Distance (Å)
BH₃	1.19
BBr₃	1.93
GaBr₃	2.35

The bond distances of these compounds are compared and a discussion is outlined below.

Bond Distance Comparison

Changing The Ligand

Changing the ligand to a heavier ligand causes the bond length to increase and thus forming a weaker bond. Both hydrogen and bromine are X-type donors and donates 1 electron to the central atom in forming a bond. However, bromine has more electrons and thus larger orbitals and so forms longer and weaker bonds.

Changing The Central Atom

Changing the central atom to a heavier atom also causes the bond length to increase. Both boron and gallium are in group 13 and therefore forms 3 single bonds with 3 bromine atoms. However, as gallium is a bigger atom and therefore has a larger and more diffused orbitals compared to boron. This causes a weaker overlap between the central atom and ligand, resulting in weaker and longer bonds compared to the B-Br single bonds.

Bond Discission

Gaussview does not draw in bonds, where bonds might be expected

In some cases, gaussview does not draw in the bonds when they may be expected, this does not necessarily mean there is no bond. Gaussview draws bonds based on distance criteria and in some cases, the distances between atoms exceeds the pre-defined parameters, thus resulting in gaussview no drawing in bonds.

Definition of a Bond

A bond is a directional attraction between two atoms, normally an electrostatic attraction, that has a stabilising effect. In the case of covalent bonds, the valence electrons from both atoms are attracted to both nuclei and thus shared between the two nuclei and forming a covalent bond. In the case of ionic bonds, electron is transferred from an electropositive atom (normally a metal)to an electronegative atom, in doing so, the former forms a positive ion and the latter forms a negative ion. An ionic bond is therefore the electrostatic attraction between the two ions. A metallic bond is one where the metal atoms in the metal lattice donates electrons to the commonly shared 'sea of electrons', resulting in the attraction between the positive metal ion and the surrounding electrons. Weaker intermolecular bonding interactions also exists and these are due to dipole-dipole interactions. For example, differences in electronegativity between different atoms often causes the formation of dipoles, these difference in dipoles leads to dipole interactions between different molecules and can result in permanent dipoles such as hydrogen bonding (in the case of nitrogen, oxygen and fluorine) or temporary dipoles such as dispersion forces. Because of the type of interactions involved and the degree of attraction between atoms is also different. The relative strengths of the bonds, in decreasing order is covalent, ionic, metallic, hydrogen bonding, dipole-dipole interactions and london dispersion forces.

Frequency analysis for BH₃ and BBr₃

A couple of attempts to compute the frequency of BH₃ were firstly carried out in order to obtain the appropriate low frequency required. Thereafter, the frequency analysis was performed for GaBr₃ in order to compare the two different molecules.

Frequency Analysis for BH₃

[BH₃ initial frequency analysis log file]

Summary Table
Property	Value
File Name	TC_bh3_freq
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Energy	-26.61532358 a.u.
RMS Gradient Norm	0.00008198 a.u.
Dipole Moment	0.00 D
Point Group	CS

Low frequencies ---    0.0005    0.0005    0.0011   33.8055   41.5584   43.6982
Low frequencies --- 1163.5017 1213.4677 1213.5865

The first line of the frequencies are far higher than the required low frequency values. Therefore, the optimisation calculations were performed again by constraining the BH₃ geometry to D_3H.

Optimisation using D_3H point group

[BH₃ (constrained geometry) frequency analysis log file ]

Summary Table
Property	Value
File Name	TC_bh3_freq3
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
Spin	Singlet
Energy	-26.61532363 a.u.
RMS Gradient Norm	0.00000291 a.u.
Dipole Moment	0.00 D
Point Group	D3H

Item               Value     Threshold  Converged?
 Maximum Force            0.000006     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000023     0.001800     YES
 RMS     Displacement     0.000015     0.001200     YES
 Predicted change in Energy=-2.012165D-10
 Optimization completed.

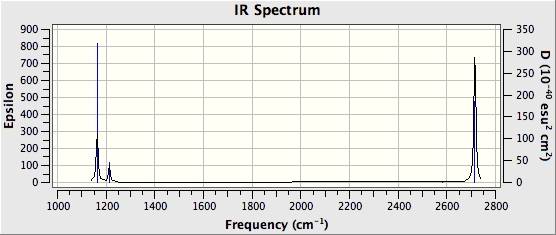
 Low frequencies ---   -0.9432   -0.8611   -0.0054    5.7455   11.7246   11.7625
 Low frequencies --- 1162.9963 1213.1826 1213.1853

No.	Form of vibration	Frequency	Intensity	Symmetry D_3H point group
1	all the hydrogens move forward and back together in a concerted motion and the boron atom move backwards and forwards in the opposite direction to the hydrogen atoms	1163	93	A₂
2	two of the hydrogens move in a scissoring fashion, the last hydrogen moves slightly up and down together with the boron atom	1213	14	E'
3	the three hydrogens all move left and right, resulting in two sets of scissoring motions	1213	14	E'
4	the hydrogen atoms all move in and out together in a concerted motion and the boron atom is stationary	2582	0	A₁'
5	two of the hydrogens moves in a asymmetric stretching fashion. The remaining hydrogen is relatively stationary with the boron atom moving slightly to the sides	2715	126	E'
6	two of the hydrogens move in a symmetrical stretching fashion with the last hydrogen moving in a asymmetrical stretching manner relative to the other two hydrogens. The boron moves slightly to the sides.	2715	126	E'

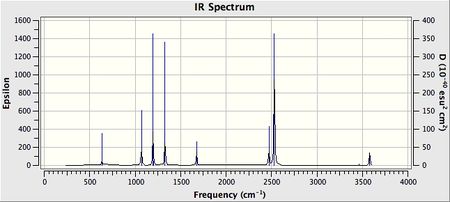
IR spectrum

There are two sets of two vibrations with the same frequencies and therefore, they would overlap and only appear as a single peak. In addition, the vibration which is totally symmetrical does not have a dipole and hence does not show up in the IR spectrum. These factors result in the IR spectrum only showing 3 peaks where there are actually six vibrations.

Frequency analysis for GaBr₃

[GaBr₃ frequency analysis D-space link] [GaBr₃ frequency analysis log file]

No.	Form of vibration	Frequency (cm^-1)	Intensity	Symmetry D_3H point group
1	two of the bromines moves in a asymmetric stretching fashion. The remaining hydrogen is relatively stationary with the gallium atom moving slightly to the sides	76	3	E'
2	two of the bromines move in a scissoring fashion, the last bromine moves slightly up and down together with the gallium atom	76	3	E'
3	all the bromines move forward and back together in a concerted motion and the gallium atom move backwards and forwards in the opposite direction to the hydrogen atoms	100	10	A₂
4	the bromine atoms all move in and out together in a concerted motion and the gallium atom is stationary	197	0	A₁'
5	two of the bromines moves in a asymmetric stretching fashion. The remaining bromine is relatively stationary with the gallium atom moving slightly to the sides	316	57	E'
6	two of the bromines move in a symmetrical stretching fashion with the last bromine moving in a asymmetrical stretching manner relative to the other two bromines. The gallium moves slightly to the sides.	316	57	E'

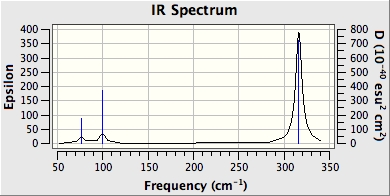
Low frequencies ---   -0.5252   -0.5247   -0.0024   -0.0010    0.0235    1.2010
Low frequencies ---   76.3744   76.3753   99.6982

The lowest "real" normal mode of vibrations are the 76 cm^-1 frequency vibrations, corresponding to the first two degenerate E' modes of vibration.

IR spectrum

There are six vibrational modes but only three peaks visible on the IR spectrum. This is because some of the vibrations are degenerate in energy (vibration 1 & 2 and vibrations 5 & 6) and so show up as a single peak. The forth vibration has no particular dipole moment, as such does not have a signal in the IR spectrum.

Vibration comparisons

No.	BH₃ vibrational frequencies (cm^-1)	GaBr₃ vibrational frequencies (cm^-1)
1	1164	76
2	1213	76
3	1213	100
4	2582	197
5	2715	316
6	2715	316

The large differences in frequency values of BH₃ compared to GaBr₃ indicate that the GaBr₃ bonds are much weaker. As suggested before the large difference between electronegativities contribute to enhanced electrostatic attraction between B and H and hence affording stronger bonds.

Although the two spectra are similar in that they both have three peaks, an reordering of modes can also be observed, in particular, the A₂ level for GaBr₃ higher in energy then its E' energy level, whereas the opposite can be seen for the BH₃ molecule. This is likely to be due to differences in the size of the atoms. For example, in the BH₃ molecule, the central atom boron is heavier than hydrogens and therefore, the substituent atoms, i.e. hydrogens, move with the central atom staying relatively stationary for the A₂ level. The case is reversed for the GaBr₃ molecule, in that the central atom is lighter than its substituent atoms and thus, the central atom vibrate more with the heavier bromine substituents relatively more stationary in the A₂ level. This difference lead to the shift in relative energies compared to their relative E' levels and hence a reordering can be seen. The vibrational frequency can be calculated using the equation:

$v = 2 π \sqrt{\frac{k}{m}}$

where k is the force constant for the restoring force: $F = - k x$

Therefore, when comparing a molecule's vibrational frequency, because a particular vibrational motion would need less force to restore, the force constant would be lower and hence the vibrational frequency would be less.

In addition, it can be seen that for both the spectra, two modes lie fairly close together, the A₂ and E', and another two modes, the A₁' and E' lie fairly close together but higher in energy. This is because for the first set of vibrations the type of vibration are all bending of the bonds, whereas, in the higher energy set of frequencies the type of vibration are all stretching vibrations. Similar type of vibration leads to similar vibrational frequencies, therefore, two sets of two modes of vibration can be seen, where one set of vibrations is close to each other and another is close to each other but higher in energy.

Nevertheless, both IR spectra exhibit the same number of modes, this is due to both molecules having the same symmetry and same number of atoms (where vibrational modes is governed by 3N-6, N=4).

The same method and basis for both the optimisation and frequency analysis much be used as the assumptions used by the one may not be compatible with the other and for both to afford correctly calculated values, the same inputs needs to be used.

The purpose of carrying out an frequency analysis is that, by investigating the frequency using computational methods, the result can be used to compare with experimental results and thus offering a higher reliability of the overall result. Also, it may be in some cases that, experimental means are not easily accessible and so computational calculations can be seen as a possible alternative method of investigation.

The top line of the low frequencies represent the translational and rotational degrees of freedom, corresponding to motion in the x, y and z axes. The bottom line of low frequencies represent the vibrational frequencies.

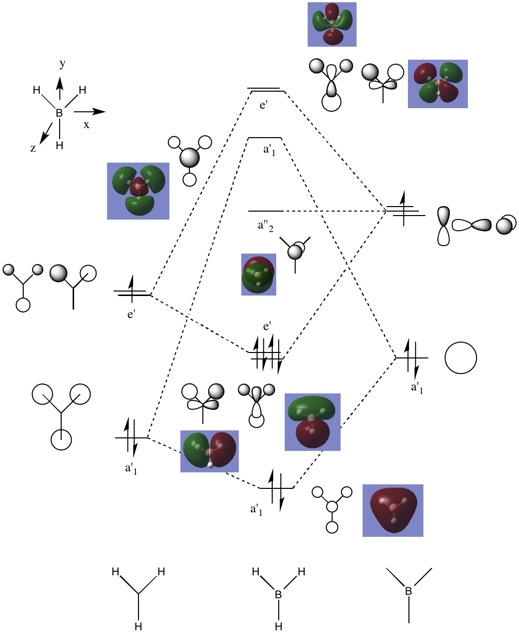
Molecular Orbitals of BH₃

A population analysis was carried out using the previously optimised BH₃ molecule with 631G(d,p) with keywords "pop=full, opt=tight, int=ultrafine, scf=conver=9"

[BH₃ population analysis D-space link] [BH₃ population analysis log file]

The LCAO MOs as predicted by the MO theory are similar to the real MO as computed by gaussian. This indicates that, while MO theory may be limited in cases where the molecule is relatively complicated, for the case of simple molecules such as BH₃, MO theory is generally accurate.

NH₃ Computational Analysis

Computational study of the NH₃ molecule was carried out in order to perform an NBO analysis.

Optimisation

The optimisation of the NH₃ molecule was performed using the 6-31G(d,p) basis set with the keywords "opt=tight, int=ultrafine, scf=conver=9"

[NH₃ optimisation log file]

Summary Table
Property	Value
File Name	NH3_opt_631G_d_p
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
Spin	Singlet
Energy	-56.55776873 a.u.
RMS Gradient Norm	0.00000323 a.u.
Dipole Moment	1.85 D
Point Group	C3V
Computational Time	29.8 Sec

         Item               Value     Threshold  Converged?
 Maximum Force            0.000006     0.000015     YES
 RMS     Force            0.000004     0.000010     YES
 Maximum Displacement     0.000012     0.000060     YES
 RMS     Displacement     0.000008     0.000040     YES
 Predicted change in Energy=-9.846059D-11
 Optimization completed.
    -- Stationary point found.

Frequency Analysis

The frequency analysis of the NH₃ molecule was carried out using the above optimised molecule with the keywords "opt=tight, int=ultrafine, scf=conver=9".

[NH₃Frequency Analysis log file]

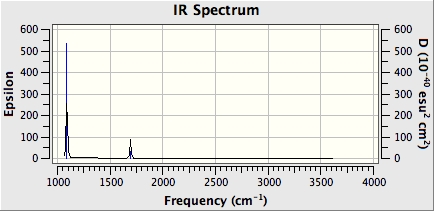
 Low frequencies ---   -0.0129   -0.0016   -0.0012    7.0768    8.0933    8.0936
 Low frequencies --- 1089.3840 1693.9368 1693.9368

Table of NH₃ Vibrational Frequencies
No.	Form of vibration	Frequency (cm^-1)	Intensity	Symmetry of C₁ point group
1	all the hydrogen atoms move downwards in a concerted motion	1089	145	A1
2	the hydrogens move in a scissoring motions with the nitrogen relatively stationary	1694	14	E
3	two of the hydrogens move in a scissoring fashion with the last hydrogen moving up and down	1694	14	E
4	all the hydrogens exhibit symmetrical stretching with the nitrogen atom relatively stationary	3461	1	A1
5	two of the hydrogens exhibit asymmetrical stretching and the remaining hydrogen relatively stationary	3590	0	E
6	two of the hydrogens vibrate in a symmetrical manner with the remaining hydrogen vibrating in an asymmetrical manner relative to the other two	3590	0	E

IR Spectrum

NH₃ IR spectrum shows two peaks only, whereas there are 6 modes of vibration. This is due to two of the modes of vibration having similar vibrations and the fact that 3 of the modes have no dipole moment and hence does not give a signal in the IR spectra.

NH3 NBO

The NBO analysis was carried out using the above optimised molecule with the keywords "pop=full, opt=tight, int=ultrafine, scf=conver=9"

[NH₃ MO analysis]

Colour Atom by Charge

It can be seen that the majority of the negative charge is resident on the nitrogen atom. This is expected as nitrogen is the atom with the relatively higher electronegativity value.

Charge range: -1.125 to 1.125

Charge Number Shown

The charge number for the various atoms are shown above (N: -1.125; H: 0.375 each). It can also be seen that the sum of all the charges adds up to zero, in accordance with NH₃ being a neutral molecule.

Information from the .log file

Additional information from the NBO analysis .log file were also investigated.

Summary of natural population analysis

    Natural Population 
                Natural  -----------------------------------------------
    Atom  No    Charge         Core      Valence    Rydberg      Total
 -----------------------------------------------------------------------
      N    1   -1.12514      1.99982     6.11104    0.01429     8.12514
      H    2    0.37505      0.00000     0.62250    0.00246     0.62495
      H    3    0.37505      0.00000     0.62250    0.00246     0.62495
      H    4    0.37505      0.00000     0.62250    0.00246     0.62495
 =======================================================================
   * Total *    0.00000      1.99982     7.97852    0.02166    10.00000

The electron density is outlined above and the majority of electrons are seen to be from nitrogen, as the nitrogen donates electron density and act of a Lewis base whereas hydrogen accepts electrons and act as a Lewis acid.

Bond orbital/Coefficient/Hydride

       (Occupancy)   Bond orbital/ Coefficients/ Hybrids
 ---------------------------------------------------------------------------------
     1. (1.99909) BD ( 1) N   1 - H   2  
                ( 68.83%)   0.8297* N   1 s( 24.86%)p 3.02( 75.05%)d 0.00(  0.09%)
                                            0.0001  0.4986  0.0059  0.0000  0.0000
                                            0.0000  0.8155  0.0277 -0.2910  0.0052
                                            0.0000  0.0000 -0.0281 -0.0087  0.0014
                ( 31.17%)   0.5583* H   2 s( 99.91%)p 0.00(  0.09%)
                                            0.9996  0.0000  0.0000 -0.0289  0.0072
     2. (1.99909) BD ( 1) N   1 - H   3  
                ( 68.83%)   0.8297* N   1 s( 24.86%)p 3.02( 75.05%)d 0.00(  0.09%)
                                            0.0001  0.4986  0.0059  0.0000 -0.7062
                                           -0.0239 -0.4077 -0.0138 -0.2910  0.0052
                                            0.0076  0.0243  0.0140  0.0044  0.0014
                ( 31.17%)   0.5583* H   3 s( 99.91%)p 0.00(  0.09%)
                                            0.9996  0.0000  0.0250  0.0145  0.0072
     3. (1.99909) BD ( 1) N   1 - H   4  
                ( 68.83%)   0.8297* N   1 s( 24.86%)p 3.02( 75.05%)d 0.00(  0.09%)
                                            0.0001  0.4986  0.0059  0.0000  0.7062
                                            0.0239 -0.4077 -0.0138 -0.2910  0.0052
                                           -0.0076 -0.0243  0.0140  0.0044  0.0014
                ( 31.17%)   0.5583* H   4 s( 99.91%)p 0.00(  0.09%)
                                            0.9996  0.0000 -0.0250  0.0145  0.0072
     4. (1.99982) CR ( 1) N   1           s(100.00%)
                                            1.0000 -0.0002  0.0000  0.0000  0.0000
                                            0.0000  0.0000  0.0000  0.0000  0.0000
                                            0.0000  0.0000  0.0000  0.0000  0.0000
     5. (1.99721) LP ( 1) N   1           s( 25.38%)p 2.94( 74.52%)d 0.00(  0.10%)
                                            0.0001  0.5036 -0.0120  0.0000  0.0000
                                            0.0000  0.0000  0.0000  0.8618 -0.0505
                                            0.0000  0.0000  0.0000  0.0000 -0.0310

The information highlights that the electrodensity in the bond are mostly from the nitrogen (~70% from nitrogen, ~30 from H)

Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis

 Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis

     Threshold for printing:   0.50 kcal/mol

As the threshold for printing is below 20 kcal/mol, the information about interaction from bonding NBOs into non-bonding or antibonding orbitals is not of interest.

Natural Bond Orbital Summary

 Natural Bond Orbitals (Summary):

                                                            Principal Delocalizations
           NBO                        Occupancy    Energy   (geminal,vicinal,remote)
 ====================================================================================
 Molecular unit  1  (H3N)
     1. BD (   1) N   1 - H   2          1.99909    -0.60417   
     2. BD (   1) N   1 - H   3          1.99909    -0.60417   
     3. BD (   1) N   1 - H   4          1.99909    -0.60417   
     4. CR (   1) N   1                  1.99982   -14.16768   
     5. LP (   1) N   1                  1.99721    -0.31757  16(v),20(v),24(v),17(v)
                                                    21(v),25(v)

The relative energies of the N-H bonds, the lone pair and core orbitals can be seen. The core orbital is very higher in energy and as such are often left off the MO diagram.

NH₃BH₃ Computational Anlysis

The optimisation, frequency analysis were completed in order to calculated the association energy for combining a molecule of NH₃ with one of BH₃.

Optimisation

The optimisation of NH₃BH₃ was completed using the basis set 6-31G(d,p) with the keywords "opt=tight, int=ultrafine, scf=conver=9".

[NH₃BH₃ optimisation analysis file]

Summary Table
Property	Value
File Name	TC_NH3BH3_opt_631g_d_p_opt_int_scf
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
Spin	Singlet
Energy	-83.22468906 a.u.
RMS Gradient Norm	0.00000124 a.u.
Dipole Moment	5.56 D
Point Group	C1
Calculation time	3 min 53.3 sec

  Item               Value     Threshold  Converged?
 Maximum Force            0.000002     0.000015     YES
 RMS     Force            0.000001     0.000010     YES
 Maximum Displacement     0.000026     0.000060     YES
 RMS     Displacement     0.000009     0.000040     YES
 Predicted change in Energy=-8.958388D-11
 Optimization completed.
    -- Stationary point found.

Frequency Analysis

The frequency analysis of NH₃BH₃ was carried out using the above optimised molecule with the keywords "opt=tight, int=ultrafine, scf=conver=9".

[NH₃BH₃ Frequency Analysis file]

 Low frequencies ---   -6.5596   -2.8712   -0.0003    0.0008    0.0009    5.6712
 Low frequencies ---  263.5388  632.9505  638.4074

No.	Form of the vibration	Frequency (cm^-1)	Intensity
1	The boron and nitrogen hydrogens all rotate forwards and backwards around the central boron-hydrogen bond in opposite directions to one another. The central atoms remain stationary	264	0
2	The central boron and nitrogen bond stretches with the hydrogen following suit, but nevertheless, stationary relative to their central atoms	633	14
3	The hydrogen atoms perform scissoring action with hydrogen from the other central atom in a symmetrical manner	638	4
4	The hydrogen atoms perform scissoring action with hydrogen from the other central atom in an asymmetrical manner	638	4
5	Two of the hydrogen atoms from the boron and nitrogen atom perform symmetrical scissoring and the remaining hydrogen perform symmetrical scissoring but in an asymmetrical manner to the other 4	1069	41
6	The hydrogen atoms all vibrate to the left and right in a concerted manner	1069	41
7	The boron hydrogens move in and out together in a concerted fashion whereas the nitrogen and its hydrogens remain stationary	1196	109
8	Two of the boron hydrogens move in a scissoring motion with the remaining hydrogen moving perpendicular to the other two, whereas the nitrogen and its hydrogens remain stationary	1204	3
9	Scissoring motion was performed by two of the boron hydrogens with the remaining hydrogen moving in a different axis to the other two, whereas the nitrogen and its hydrogens remain stationary	1204	3
10	The nitrogen hydrogens move in and out together in a concerted fashion whereas the boron and its hydrogens remain stationary	1329	114
11	Two of the boron hydrogens move in a scissoring motion with the remaining hydrogen moving perpendicular to the other two, whereas the nitrogen and its hydrogens remain stationary	1676	28
12	Scissoring motion was performed by two of the nitrogen hydrogens with the remaining hydrogen moving in a different axis to the other two, whereas the boron and its hydrogens remain stationary	1676	28
13	The boron hydrogen atoms all undergo concerted symmetrical stretching. The boron atom as well as the nitrogen and its hydrogens remain stationary	2472	67
14	Two of the boron hydrogens exhibit asymmetric stretching with the remaining hydrogen and the boron atom moving slightly to compensate for the stretching. The nitrogen atom and its hydrogens are relatively stationary	2532	231
15	Two of the boron hydrogens perform symmetrical stretching with the remaining hydrogen exhibiting an asymmetric stretching pattern compared to the other two boron hydrogens. The nitrogen atom and its hydrogens remain stationary	2532	231
16	The nitrogen hydrogen atoms all undergo concerted symmetrical stretching. The nitrogen atom as well as the boron and its hydrogens remain stationary	3464	3
17	Two of the nitrogen hydrogens exhibit asymmetric stretching with the remaining hydrogen and the nitrogen atom moving slightly to compensate for the stretching. The boron atom and its hydrogens are relatively stationary	3581	28
18	Two of the nitrogen hydrogens perform symmetrical stretching with the remaining hydrogen exhibiting an asymmetric stretching pattern compared to the other two nitrogen hydrogens. The boron atom and its hydrogens remain stationary	3581	28

NH₃BH₃ IR Spectrum

Below is the IR spectrum from the frequency analysis calculations.

Association Energy

An analysis of the association energy for combining a molecule of NH₃ with one of BH₃ is outlined below:

Table of Reactant and Product Energies
Molecule	Energy (a.u.)
BH₃	-26.61532358
NH₃	-56.55776873
NH₃BH₃	-83.22468906

The bond energy is the energy difference between the reactants and products. This can be calculated according to the equation:

$Δ E = E (N H_{3} B H_{3}) - (E (B H_{3}) + E (N H_{3}))$

$Δ E = - 83.22468906 (a . u .) - ((- 26.61532358 (a . u .)) + (- 56.55776873 (a . u .)))$

$Δ E = - 0.05159675 (a . u .)$

The energy value can be converted from AU to kJ/mol by multiplying the AU energy value by N_a and a factor of 4.359810x10^-18 and dividing by 1000:

$Δ E = - 135.49 k J / m o l$

The calculated bond energy is reasonable as it is within the range of normal bond energies, i.e. within the range of ~100 kJ/mol - ~500kJ/mol. In addition, the calculated value is negative, which indicate that the process of forming NH₃ is favourable and therefore spontaneous process. The bond energy is +135.49 kJ/mol.

References

↑ K. Kawaguchi, J Chem Phys , 1992, 96, 3411-3415 DOI: 10.1063/1.461942
↑ B. Reffy, M. Hargittai, M. Kolonits and B. Reffy, J. Mol. Struct., 1998 , 445, 139 - 148 DOI: 10.1016/S0022-2860(97)00420-1
↑ I. Krossing and G. Santiso-Quinones, Z. Anorg. Allg. Chem., 2008, 634, 4, 704 - 707 DOI: 10.1002/zaac.200700510

[1] K. Kawaguchi, J Chem Phys , 1992, 96, 3411-3415 DOI: 10.1063/1.461942

[2] B. Reffy, M. Hargittai, M. Kolonits and B. Reffy, J. Mol. Struct., 1998 , 445, 139 - 148 DOI: 10.1016/S0022-2860(97)00420-1

[3] I. Krossing and G. Santiso-Quinones, Z. Anorg. Allg. Chem., 2008, 634, 4, 704 - 707 DOI: 10.1002/zaac.200700510

[1]

[2]

[3]

BH3 molecule Optimisation

3-21G Basis Set

6-31G Basis Set

Total Energies

GaBr3 Optimisation

BBr3 Optimisation

Item Table

Bond comparison of BH3 BBr3 and GaBr3

Bond Distance Comparison

Changing The Ligand

Changing The Central Atom

Bond Discission

Gaussview does not draw in bonds, where bonds might be expected

Definition of a Bond

Frequency analysis for BH3 and BBr3

Frequency Analysis for BH3

Optimisation using D3H point group

IR spectrum

Frequency analysis for GaBr3

IR spectrum

Vibration comparisons

Molecular Orbitals of BH3

NH3 Computational Analysis

Optimisation

Frequency Analysis

IR Spectrum

NH3 NBO

Colour Atom by Charge

Charge Number Shown

Information from the .log file

Summary of natural population analysis

Bond orbital/Coefficient/Hydride

Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis

Natural Bond Orbital Summary

NH3BH3 Computational Anlysis

Optimisation

Frequency Analysis

NH3BH3 IR Spectrum

Association Energy

References

BH₃ molecule Optimisation

GaBr₃ Optimisation

BBr₃ Optimisation

Bond comparison of BH₃ BBr₃ and GaBr₃

Frequency analysis for BH₃ and BBr₃

Frequency Analysis for BH₃

Optimisation using D_3H point group

Frequency analysis for GaBr₃

Molecular Orbitals of BH₃

NH₃ Computational Analysis

NH₃BH₃ Computational Anlysis

NH₃BH₃ IR Spectrum