Jump to content

Rep:Mod:TWXXVIII

From ChemWiki

Experiment 1C: Part 1

Conformational analysis using Molecular Mechanics

Dimerisation and subsequent hydrogenation of cyclopentadiene

Cyclopentadiene has proven to be one of the most useful molecules in the last century with respect to the inorganic phenomenon of metallocenes. For use as an organic ligand it is first required to 'crack' commercially available mixtures of cyclopentadiene dimers at >150°C to recover the monomer for experimental procedure. This is particularly necessary because the aforementioned Diels-Alder dimerisation readily takes place at room temperature. In this experiment the energy of relative endo/exo conformers were examined to determine whether the dimerisation process is under kinetic or thermodynamic control. In the second step of this experiment the same molecular mechanics predictions are made for the two possible dihydro derivatives of the endo-dicyclopentadiene dimer.


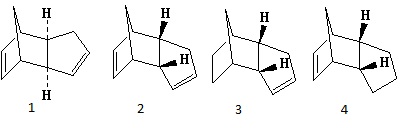
Figure 1: Dimerisation and hydrogenation products


Table 1: Energy contributions to dimerisation and hydrogenation products
(All units kcal/mol) Molecule 1 Molecule 2 Molecule 3 Molecule 4
Stretch 1.2850 1.2508 1.0965 1.2489
Bend 20.5805 20.8478 14.5244 19.1610
Stretch-Bend -0.8380 -0.8358 -0.5494 -0.8354
Torsion 7.6555 9.5109 12.4974 11.0729
Non-1,4 VDW -1.4174 -1.5439 -1.0701 -1.6416
1,4 VDW 4.2333 4.3201 4.5126 5.7963
Dipole/Dipole 0.3775 0.4476 0.1406 0.1622
Total Energy 31.8764 33.9975 31.1520 34.9643


The dimerisation of cyclopentadiene can yield either the exo (Molecule 1) or endo (Molecule 2) product, shown in Figure 1. With regards to the minimized energy contributions produced by the MM2 force field in ChemBio3D (shown in Table 1), it is evident that the exo product is lower in total energy by approximately 2 kcal/mol and can hence be labelled the thermodynamic product. Upon further comparison of results, the significant factor appears to be the torsional strain, of which the endo dimer is approximately 2 kcal/mol higher in energy than the exo dimer. This increase in torsion arises from the reduced distance between the two rings. Nonetheless it is documented by Woodward and Hoffmann that the Diels-Alder reaction between two cyclopentadiene monomers favours the endo dimer. The interactions between occupied and unoccupied orbitals owe to favourable orbital symmetry which result in a lower transition state energy.[1]
Once again, the structures of possible hydrogenation products were drawn out in ChemBio3D and minimised in energy using the MM2 force field. It proved useful once more to draw a comparison between the energy contributions to both dihydro derivatives. The distinguishing factor in this case was the bending energy, a difference of almost 5 kcal/mol. It is clear to see that molecule 4 will suffer from a form of strain on the bond angles either side of the double bond due to the neighbouring bridging carbon atom. In contrast the position of the double bond in molecule 3 allows for a less-strained bending motion. This is confirmed by the bond angles about the sp2 carbon atom (107.6° for molecule 4 and 112.9° for molecule 3) exhibiting a closer proximity to the optimum 120° angle in molecule 3. It is confirmed in the literature that molecule 3 is the major product[2] and so in conjunction with the simulation results it is logical to define the hydrogenation of dicyclopentadiene to be under thermodynamic control.

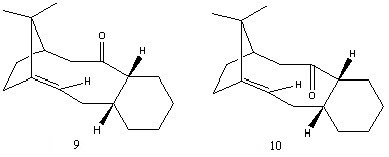
Atropisomerism in an Intermediate related to the Synthesis of Taxol

Figure 2: Related Taxol intermediates

During the synthetic procedure of the ovarian cancer drug Taxol it is found that a form of atropisomerism concerning the carbonyl functional group exists. Both of these stereoisomers are shown in Figure 2. The aim for this part of the experiment was to explore which of the two atropisomers was the most stable. From this point we could then go some distance to recognizing the most likely form of the intermediate. Furthermore, this information was used to clarify why the alkene functional group is found to react slower than expected. [3]
The procedure followed was identical to the previous section; using ChemBio3D to draw each molecule and minimize the energy using the MM2 forcefield. The hydrogenated products of each intermediate were also examined to understand the reported hyperstabilisation of the aforementioned alkenes.
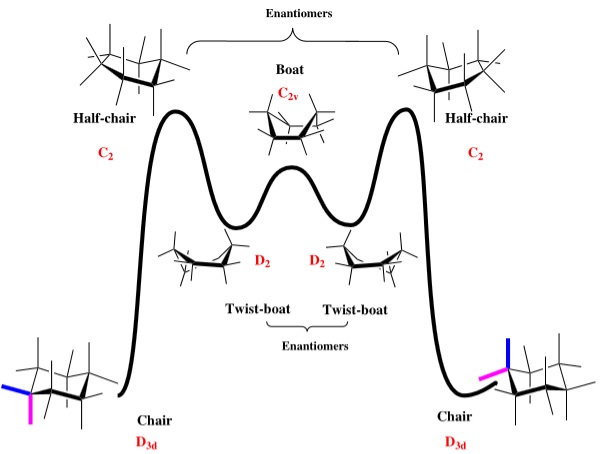
The inclusion of a cyclohexane ring in the intermediate molecule leads to the possibility of four conformers (two chairs and two twist-boats) per atropisomer. Figure 3 exhibits the various conformers associated with a cyclohexane ring, suggesting that the lowest energy conformation for each molecule will be a chair. Nonetheless, the total energies are included for all 8 possible conformations in Table 2.

Figure 3: Relative energies of cyclohexane conformations
Table 2: Total Energy of conformers of molecules 9 and 10
Molecule 9 Molecule 10
Conformation Chair 1 Chair 2 Twist-boat 1 Twist-boat 2 Chair 1 Chair 2 Twist-boat 1 Twist-boat 2
Total Energy (kcal/mol) 47.8395 58.3856 53.0099 53.3043 41.3808 52.5418 56.0758 56.0361



It is observed that for both molecules one of the chair conformers is notably lower. The respective low-energy chair conformers of molecules 9 and 10 were directly compared to evaluate the stability of the intermediate. Upon a quick comparison with Figure 3 it is apparent that molecule 10 follows the pattern of both chair conformers existing at a lower energy than either of the twist-boat conformers. Contrarily this is not the case for molecule 9 which appears to have both twist-boats at a lower energy than one of the chair conformers. This chair conformer is higher in energy than this twist-boat conformer, which originates from the difference of ≈4 kcal/mol in the bending energy contribution.
It is once again necessary to analyze the data in Table 3 and comprehend the origin of the total energy difference. The only major contrast is the bending energy which is favorable in molecule 10 by ≈5 kcal/mol. A resulting inspection of the bond angles around the carbonyl carbon show a complimentary angle of 119.0° in molecule 10 as opposed to 115.7° in molecule 9. This difference in energy is the reason that upon standing (thermodynamic conditions) the more stable atropisomer, molecule 10, is formed.

Table 3: Energy contributions to lowest energy conformers of molecules 9 and 10
(All units kcal/mol) Molecule 9 Molecule 10
Stretch 2.7846 2.6015
Bend 16.5412 10.4216
Stretch-Bend 0.4304 0.2909
Torsion 18.2511 19.3717
Non-1,4 VDW -1.5524 -2.2170
1,4 VDW 13.1093 12.9213
Dipole/Dipole -1.7248 -2.0091
Total Energy 47.8395 41.3808

It was raised in the script that the aforementioned alkenes are known to react very slowly, indicating the effect of so-called hyperstable olefins. These are alkenes which show reduced reactivity when compared with their parent alkanes, often in the proximity of a bridgehead. It is documented in the literature that vicinal and transannular interactions between hydrogens are a cause for the molecule's unusually low reactivity.[4] The hydrogenated products of molecules 9 and 10 were modelled and their bond angles(around the base of the bridgehead in the former alkene-position)were measured to be 120.9° and 122.6° respectively. Considering that these bond angles encompass an sp3 carbon centre, they are both significantly removed from the optimal 109.5°, consolidating their instability with respect to the alkene. The strain, coupled with the additional increase of sterics (2 more hydrogen atoms), will also contribute to the instability of the parent alkane.

Spectroscopic Simulation using Quantum Mechanics

Figure 4: Molecule 18

In this part of the assignment quantum mechanics was utilised in order to predict both the 1H and 13C NMR spectra for a derivative of the taxol intermediates discussed in the previous section (in this case, the most stable one).[5] The simulated results were compared to values found in the literature[6] and further discussed regarding their assignment in the original article.

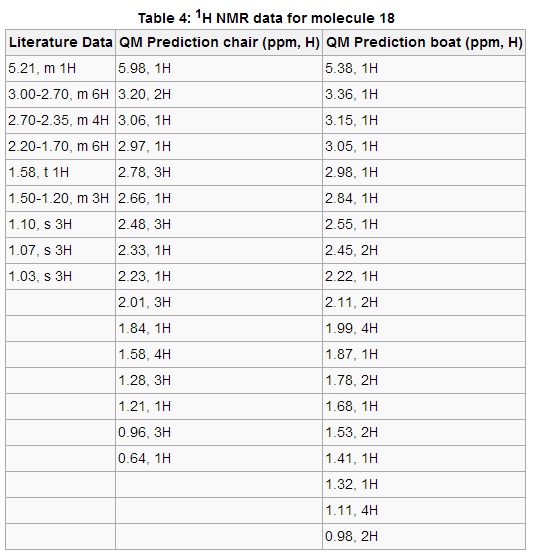
The functionality of molecule 18 allows for multiple conformations, therefore it was decided that both the chair and the boat conformers of molecule 18 would be simulated with an interest to detect any discrepancies between the two. Both conformers were drawn in ChemBio3D with attention paid to the methyl branch alpha to the carbonyl group, ensuring that both said methyl and neighbouring hydrogen were syn. Anything otherwise would affect the Gaussian output. The geometries were optimized and the energies were minimized in Avagadro using the MMFF94s force field, after which the spectra were calculated using Gaussian. Table 4 displays the 1H NMR data predicted by Gaussian, showing reasonable similarity between the values predicted for the boat conformer and the literature data. It should be mentioned that the multiplets recorded in the literature are almost certainly a mixture of separate signals in the same chemical shift range, causing a degree of confusion on the experimental NMR spectrum. As mentioned before, the boat conformer provides a closer fit to the literature spectrum. The signal at 5.38 ppm represents the alkene proton and only lies 0.17 ppm further downfield than the literature value. The following 6 hydrogens in the 3.36-2.55 ppm range correspond to multiplet between 3.00-2.70 ppm in the literature. The subsequent 4H and 6H multiplets in the literature are vaguely mirrored by the protons in the predicted range of 2.45-1.87 ppm. The subsequent, well-defined triplet at 1.58 ppm is not replicated in the simulation, although there is modest correlation regarding chemical shift patterns. The degeneracy (i.e, proton integrals) tends to diverge from the literature at low chemical shifts.

Figure 5: Simulated 1H NMR Spectrum for chair conformation
Figure 6: Simulated 1H NMR Spectrum for boat conformation
Figure 7: Simulated 13C NMR Spectrum for chair conformation
Figure 8: Simulated 13C NMR Spectrum for boat conformation

The output values from Gaussian for the chair conformer agree less with the literature. The signal representing the alkene proton is shifted much more downfield at 5.98 ppm compared the boat conformer. The degeneracy of the protons theoretically corresponding to the 6H and 4H multiplets fits poorly, as do the chemical shift ranges at the downfield region of the spectrum. For example 0.63 ppm does not correlate well to the lowest signal (1.03 ppm) on the literature spectrum. Between the two simulations themselves the faint correlation culminates in a resemblance between the proton signals at 3.20 and 3.36 ppm for the chair and boat respectively. The overall arrangement of chemical shifts is similar, although discrepancies somehow arise in the peak integrals which can disrupt the assignment of signals. In theory, the chemical shifts are expected to vary between conformers particularly due to the change in environments of the protons around the cyclohexane ring. The multiplicity should remain constant due to the identical connectivity in each conformer. The 13C NMR data in Table 5 shows a much more specific similarity in terms of chemical shift comparisons. The prediction values compare well both to the other conformation and to the literature. With the exception of two signals, all predicted values are within a 5 ppm range of the literature figures. The most notable anomaly to this statement are the signals corresponding to the carbon bonded to two sulfur atoms, in the literature at 74.61 ppm. This has most probably arisen from a spin-orbit coupling error, where carbon atoms are bonded to heavy elements. There is also the possibility that the calculation was not performed on the genuine lowest-energy conformer, although the wide inaccuracy suggests the former reason is more plausible. When comparing both predicted spectra it is evident that only delicate differences exist. On average, the difference in chemical shift between boat and chair conformations is approximately 2.5 ppm, which is rather precise on a scale of 191 ppm. Such small variations imply that the carbon environments are effectively the same in both conformers, an outcome to be expected considering the chemical bonding of each carbon atom is exactly the same.

References

  1. ↑ R. Hoffmann and R. B. Woodward, "The Conservation of Orbital Symmetry", Acc. Chem. Res., 1968, 1, 17-22.
  2. ↑ G. Liu, Z. Mi, L. Wang and X. Zhang, "Kinetics of Dicyclopentadiene Hydrogenation over PdAl2O3 Catalyst", Ind. Eng. Chem. Res., 2005, 44, 3846-3851.DOI:10.1021/ie0487437
  3. ↑ W. F. Maier and P. Von Rague Schleyer, "Evaluation and prediction of the stability of bridgehead olefins", J. Am. Chem. Soc., 1981, 121, 6337-6343. DOI:10.1021/ja00398a003
  4. ↑ S. Vazquez and P. Camps, "Chemistry of pyramidalized alkenes", Tett., 2005, 61, 5147-5208. DOI:10.1016/j.tet.2005.03.055
  5. ↑ L. A. Paquette, K. D. Combrink, S. W. Elmore, R. D. Rogers, J. Am. Chem. Soc., 1991, 113, 1335-1344.DOI:10.1021/ja00004a040
  6. ↑ L. A. Paquette, N. A. Pegg, D. Toops, G. D. Maynard and R. D. Rogers, J. Am. Chem. Soc., 1990, 112, 277-283. DOI:10.1021/ja00157a043

Experiment 1C: Part 2

Crystal Structures of Shi and Jacobsen catalyst precursors

In the first part of this section it was interesting to analyze the crystal structures for each catalyst precursor, which would go some way to uncovering the reasons behind issues of selectivity.

Figure 9: Catalyst precursors

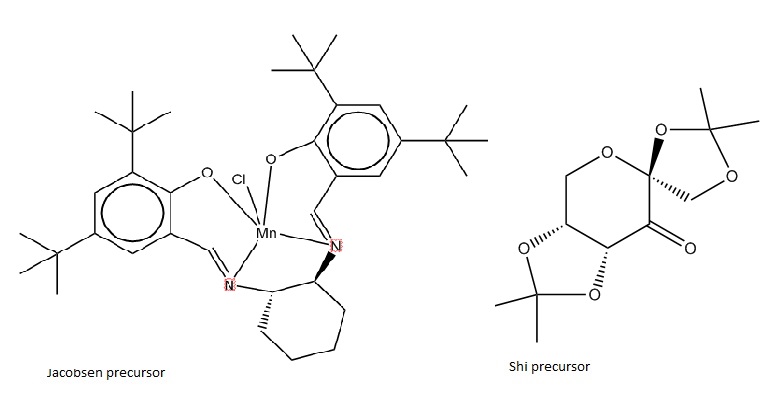
The Cambridge crystal database was searched for the pre-catalyst structures (shown in Figure 9) using the program Conquest. Once the crystal structures had been located, Mercury software was used to scrutinize various bond lengths and steric effects.
The Shi catalyst is well-known for the absence of any metal centres, and for its ability to epoxidise trans- or tri-substituted alkenes with great efficiency.[1] When examining the jmol of the Shi catalyst precursor it is first apparent that 3 anomeric centres exist in the molecule (one in each of the 5-membered rings as well as in the 6-membered central ring). When the catalyst is active, so to say the ketone functionality is replaced by a dioxirane group, it can be observed that the directionality of the 5-membered rings is sterically a problem for cis- substituted alkenes wishing to approach the reaction centre.

Figure 10: Bond lengths associated with Shi precursor anomeric centres

Figure 10 illustrates the difference of bond lengths regarding the two types of anomeric centre. The anomeric centres in the 5-membered rings have a difference of approximately 0.03Å between C-O bond lengths whereas the anomeric centre in the 6-membered ring has a mere 0.008Å difference. The explanation for this lies with the anomeric effect, where a form of stabilisation takes place between the lone pair of the heteroatom member of the ring and a σ* orbital of

an axial C-O bond. [2] This form of hyperconjugation will strengthen one of the two C-O bonds and hence cause a difference in bond lengths. This effect is strongest in the two 5-membered ring anomeric centres, where the geometry is optimal for orbital overlap and therefore hyperconjugation. It is also worth mentioning that each anomeric centre in a 5-membered ring bonded to an oxygen contains at least 6 favourable anti-periplanar interactions between σC-O/σ*C-H orbitals, originating from terminal methyl groups on either end of the Shi catalyst. These contributions to the E(2) stabilization energies for each C-O bond are similar and not the deciding factor in difference of bond lengths.

For the Jacobsen precursor attention was turned to the tert-butyl groups on each phenyl ring. To fully understand their role, the display of the catalyst precursor was set to spacefill, as shown in Figure 11.

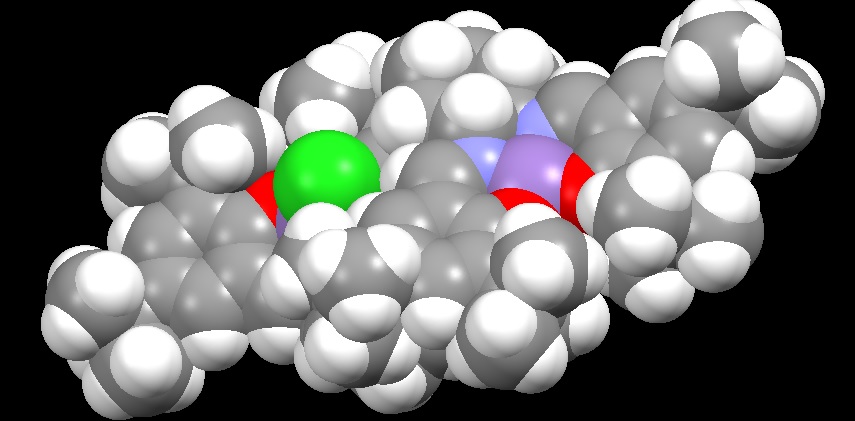
Figure 11: Spacefill display of Jacobsen precursor (The purple sphere represents Mn)

The first step in activating the precursor requires the displacement of the chlorine atom by an incoming oxygen, usually provided by NaOCl. Once the manganese-oxygen double bond is formed it is susceptible to attack by an alkene. Figure 11 demonstrates the role of the t-butyl groups by blocking any sort of alkene attack from the side of the molecule, which would result in a different stereochemical outcome. The sheer amount of space occupied by the t-butyl groups also ensures that only Z-alkenes are likely to attack because of the steric clash that would occur with corresponding E-isomer. From Mercury we can also view the distances between hydrogens on different methyl branches. All of these lengths are greater than 0.2 nm and so we can forecast the existence of attractive dispersion forces between them.[3]


Calculated 1H and 13 NMR data for epoxides

It would undoubtedly prove useful to investigate the NMR spectra of each chosen epoxide and make comparisons to the literature[4] as seen in Part 1. Upon first impression the predicted and experimental data appear much more comparable than seen previously with the Taxol intermediate, most probably owing to the relative simplicity of the scrutinized epoxides.

Only the spectra of one enantiomer is included in this wiki because they are identical, which means that the configuration cannot be assigned based on NMR data.
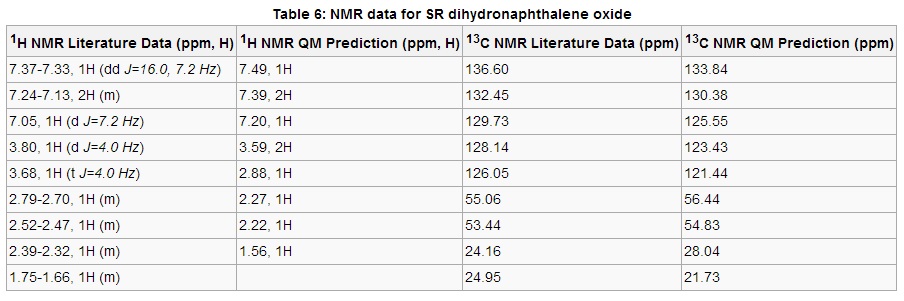
The 1H NMR data in Table 6 shows a strong correlation; emulating the correct chemical shift regions as well as proton degeneracies. This is also the case for the 13C NMR data which again simulates an accurate breakdown of signals at specific chemical shifts, with the largest inaccuracy in chemical shift being 4.7 ppm.
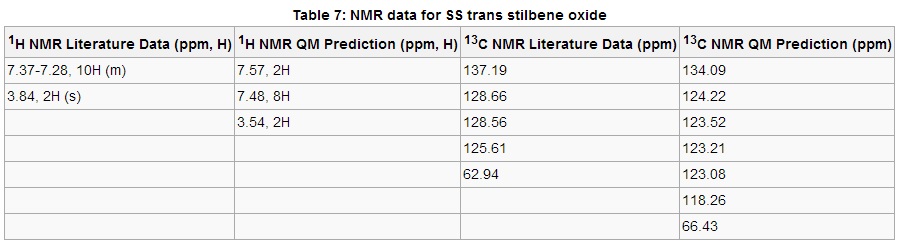
Table 7 exhibits the NMR data for SS trans stilbene oxide which again predicts the chemical shift ranges and degeneracy well. Perhaps the only note concerning the 1H NMR data is that Gaussian perhaps over accounts for the proximity of two hydrogens to the electronegative oxygen atom of the epoxide, resulting in a separate 2H signal at 7.57 ppm. The 13C data compares well with the literature, although two less signals appear in the literature. One can deduce that the missing signals correspond to some of the aromatic carbon atoms at around 125 ppm. Apart from that, the predicted signals corresponding to the carbons in the epoxide group are within 4 ppm of the literature data.

Note: The .log files used to observe coupling constants for both (S,S)-trans-stilbene oxide and (S,R)-dihydronaphthalene oxide can be obtained by clicking the hyperlinks. The matrices were analysed very briefly, in particular looking at J values to confirm the presence of the correct number of environments of aromatic protons. Unfortunately the time required to completely decipher both matrices and present the data in a reasonable format proved too cumbersome.

Assigning the absolute configuration of epoxides

Calculated chiroptical properties

The geometrically optimized output files from the NMR calculations were used to find the optical rotation of each epoxide enantiomer. Each calculation used a light of incident wavelength 589 nm and were submitted as a 4 processor job to the HPC.

Table 8: Calculated optical rotations for dihydronaphthalene oxide and trans-stilbene oxide
(R,S)-dihydronaphthalene oxide (S,R)-dihydronaphthalene oxide (S,S)-trans-stilbene oxide (R,R)-trans-stilbene oxide
-155.82° 155.82° -297.88° 297.88°

A wide range of results unearthed by a literature search negated any real prospects of assigning the absolute configuration of the epoxides based on optical rotation. All articles, however, matched the polarity of rotation for each respective enantiomer computed by Gaussian, with some even coming close to matching the specific figure (144.9° for dihydronaphthalene oxide[5] and 296° for trans-stilbene oxide[6]).

Transition state properties of Shi epoxidation

Figure 11: Lowest energy transition state of (R,R)-trans-stilbene oxide
Figure 12: Lowest energy transition state of (S,S)-trans-stilbene oxide

From the given transition states in the script, it was possible to determine the respective Gibbs free energies and in turn the most likely transition state to occur for each enantiomer. The lowest energy transition state was selected in order to calculate the equilibrium constant K using the equation ΔG=-RTlnK.

The most stable transition overall in the epoxidation of trans-stilbene oxide, originating from the (R,R) enantiomer (the first jmol), is -1534.700037 Hartree. The lowest transition for the (S,S) enantiomer is -1534.693818 Hartree. The energy difference equals +16.327982 kJ/mol which results in a K value of 0.001378. This K value reflects the enantiomeric excess, in this case showing that the (R,R) configuration of trans-stilbene is 99.86% favoured.

Figure 14: Energy differences and diagram of planar transition state[7]

Figure 14 shows the relative energy differences for varying synchronous/asynchronous and planar/spiro combinations of the transition state. It should be mentioned that the lower energy approach, spiro, has a roughly 45° angle between the position of the alkene bond and the R groups attached to the dioxirane carbon, i.e, the R substituents are not overlapping the double bond position as shown in the planar structure in Figure 14. The inclination for the transition state to adopt the spiro approach is because of non-bonding orbital interactions between the oxygen lone pair orbital and the π* orbital of the alkene bond.[7] The literature confirms such high values of enantiomeric excess using the Shi catalyst.[8]

Similar calculations were carried out with respect to the different configurations of 1,2-dihydronaphthalene; the energy difference between the most stable transition pathways was 5.723589 kJ/mol resulting in an ee value of 90.97% in favour of the (S,R) enantiomer. This figure roughly agrees with the literature value of 84%.[9]

Transition state properties of Jacobsen epoxidation

Lowest energy transition state of (S,R)-phenylprop-1-ene oxide
Lowest energy transition state of (R,S)-phenylprop-1-ene oxide

An investigation into the mechanism behind the reaction of Jacobsen's catalyst with phenylprop-1-ene was carried out using pre-determined transition states in the script. The axial oxygen in the Mn complex is responsible for the attack on the carbon-carbon double bond. The difference between the two lowest-energy transition states shown above is the direction from which the alkene approaches. The enantiomeric excess of the (S,R) epoxide (the first jmol) was 99.98% owing to the energy difference of 22.314125 kJ/mol between transition states. These findings wholly agree with that of the literature.[10] The relatively small size of phenylprop-1-ene allows it to avert the potential steric hindrance with t-butyl groups mentioned earlier in this article, hence allowing it to approach the oxygen from directly above one one of the imine groups or alternatively to approach over the unsubstituted cyclohexane ring.[11]

Investigating NCI in the active-site of the reaction transition state

Orbital

In this section Gaussview was used to generate a visual representation of non-covalent interactions. This served as an aid in defining the mechanistic action of the epoxidation of trans-stilbene.
The Jmol above depicts the non-covalent interactions of interest. Firstly it should be noted that the blue ring above the former double bond is the bond forming region and is not of particular interest in this analysis. However, the multi-coloured feature of the ring is due to the stabilising bond formation as well as strongly repulsive oxygen 'lone pair-pi orbital interactions'. The areas of green represent mild attractive interactions whereas the red and yellow areas represent strong and mild repulsions respectively. The major band of attraction appears to be localised on one side of the alkene, encircling one half the bond-forming region from above the aromatic ortho- hydrogens on each of the phenyl rings. The smaller green isosurfaces between terminal methyl hydrogens and hydrogens attached to a ring are expected to be van der Waals interactions. Areas of unfavourable intereactions occur in the centre of the 5-membered rings of the Shi catalyst, most probably arising from the close proximity of two oxygen atoms (and hence their lone pairs) in the acetal functional group.

Investigating the electronic topology in the active-site of the reaction transition state

Further to the previous analytical method, the same (R,R)-trans-stilbene transition state was the subject of QTAIM analysis. The Bond Critical Points illustrate where the electron density is highest, therefore indicating the presence of bonds or various stabilising interactions.
If we compare the location of the BCPs in carbon-carbon bonds with the corresponding point in carbon-hydrogen bonds we can see that the electron density maxima are split equidistant from either carbon atom, whereas in C-H bonds the maxima lay closer to the hydrogen atom due to it's slight increase in electronegativity. Such information is not insightful as it merely validates known information regarding covalent bonds.
Instead, attention is turned to molecular interactions. For example, it is implied in Figure 10 that hydrogen bonding occurs between the oxygen atom in the 6-membered ring and a terminal hydrogen. It is acknowledged that such BCPs may not guarantee the presence of hydrogen bonding, but qualitatively suggest their existence.[12] The same applies to the interaction shown in Figure 11, although this time the stabilising interaction is between the Shi catalyst and substrate alkene. This effect, coupled with dispersion forces between hydrogen and non-polar carbon atoms contribute to the mild attractive isosurface shown in the NCI model above. In the centre of the picture we can witness the active site of epoxidation, where one of the oxygen atoms from the catalyst's dioxirane functionality is introduced across the alkene double bond,.

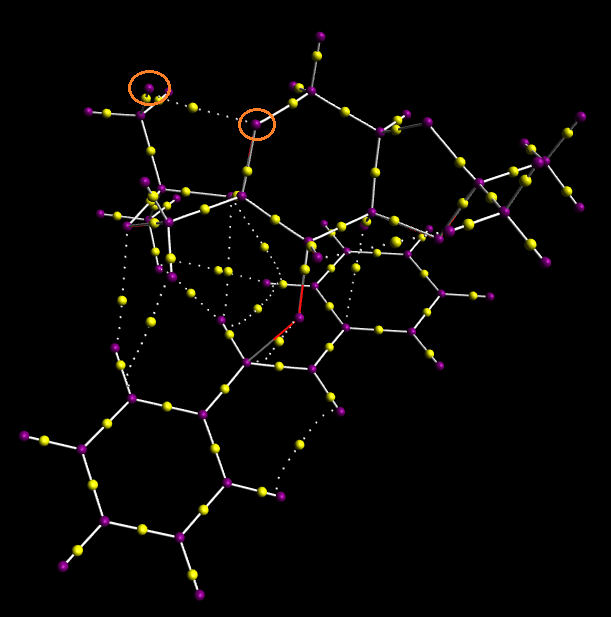
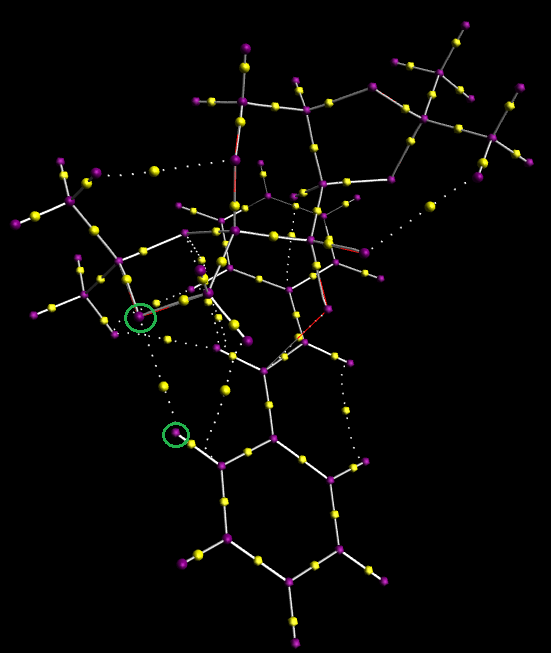
Figure 10: Intramolecular hydrogen bonding
Figure 11: Intermolecular hydrogen bonding

The stabilising intermolecular interactions form a favored transition state which results in high enantioselectivity. It is worth mentioning that Z-alkenes would react less effectively due to the increased distance between non-covalently interacting atoms. Fewer of these stabilising interactions would reduce product selectivity.

Suggested new candidates

Figure 15: Pulegone

A quick Reaxys epoxide substructure search of potentially interesting alkenes (and subsequent epoxides) to investigate returned a molecule called p-Menth-4(8)-en-3-one, but perhaps commonly known as pulegone. The parent alkene is shown in Figure 14. The ORP of pulegone oxide is 786.5° at 293 nm[13] which means it has sufficient optical activity to examine computationally. Both enantiomers are available to purchase from Sigma Aldrich which offers the option to carry out the experimental procedure in undergraduate laboratories.


References

  1. ↑ A. Burke, P. Dillon, K. Martin and T. W. Hanks, "Catalytic Asymmetric Epoxidation Using a Fructose-Derived Catalyst", J. Chem. Educ., 2000, 77, 271.DOI:10.1021/ed077p271
  2. ↑ V. Box, "The Role of Lone Pair Interactions in the Chemistry of the Monosaccharides", Heterocycles, 1991, 32, 795-807.DOI:10.3987/REV-91-425
  3. ↑ M. Mantina, A. C. Chamberlin, R. Valero, C. J. Cramer and D. G. Truhlar, "Consistent van der Waals Radii for the Whole Main Group", J. Phys. Chem. A, 2009, 113, 5806-5812.DOI:10.1021/jp8111556
  4. ↑ B. R. Buckley, Y. Chan, N. Dreyfus, C. Elliott, F. Marken and P. C. B. Page, "Harnessing applied potential to oxidation in water", Green Chem., 2012, 14, 2221-2225.DOI:10.1039/C2GC35238A
  5. ↑ H. Sasaki, R. Irie, T. Hamada, K. Suzuki and T. Katsuki, "Rational design of Mn-salen catalyst (2): Highly enantioselective epoxidation of conjugated cis olefins", Tet., 1994, 50, 11827-11838.DOI:10.1016/S0040-4020(01)89298-X
  6. ↑ A. Solladie-Cavallo, A. Diep-Vohuule, V. Sunjic and V. Vinkovic, "A two-step asymmetric synthesis of pure trans-(R,R)-diaryl-epoxides", Tet., 1996, 7, 1783-1788.DOI:10.1016/0957-4166(96)00213-3
  7. ↑ 7.0 7.1 K. N. Houk, J. Liu, N. C. DeMello and K. R. Condroski, "Transition States of Epoxidations: Diradical Character, Spiro Geometries, Transition State Flexibility, and the Origins of Stereoselectivity", J. Am. Chem. Soc., 1997, 119, 10147-10152.
  8. ↑ H. Tian, X. She, J. Xu and Y. Shi, "Enantioselective Epoxidation of Terminal Olefins by Chiral Dioxirane", Org. Lett., 2001, 3, 1929-1931.DOI:10.1021/ol010066e
  9. ↑ K. Nakata, T. Takeda, J. Mihara, T. Hamada, R. Irie and T. Katsuki, "Asymmetric Epoxidation with a Photoactivated [Ru(salen)] Complex", Chem. Eur. J., 2001, 7, 3776-3782.
  10. ↑ E. N. Jacobsen, W. Zhang, A. R. Muci, J. R. Ecker and L. Deng, "Highly enantioselective epoxidation catalysts derived from 1,2-diaminocyclohexane", J. Am. Chem. Soc., 1991, 113, 7063-7064.DOI:10.1021/ja00018a068
  11. ↑ T. Linker, "The Jacobsen–Katsuki Epoxidation and Its Controversial Mechanism", Angew. Chem. Int. Ed. Eng., 1997, 36, 2060-2062.DOI:10.1002/anie.199720601
  12. ↑ J. R. Lane, J. Contreras-Garcia, J-P. Piquemal, B. J. Miller and H. G. Kjaergaard, "Are Bond Critical Points Really Critical for Hydrogen Bonding?", J. Chem. Theory Comput., 2013, 9, 3263-3266.DOI:10.1021/ct400420r
  13. ↑ P. M. Dansette, H. Ziffer and D. M. Jerina, "Optically active 4-substituted cis-1,2-diphenylethylene oxides and related 1,2-diphenylethane diols", Tet., 1976, 17, 2071-2074.DOI:10.1016/0040-4020(76)85110-1
Retrieved from "https://chemwiki.ch.ic.ac.uk/index.php?title=Rep:Mod:TWXXVIII&oldid=818080"