Rep:Mod:TSams1015
Introduction
Throughout this computational lab we investigated the properties and MO energies of reactants and their resulting transition states. Various optimisation methods were used in Gaussian which will be explored further in this report. Intrinsic reaction coordinates were also explored for some reactions.
Quantum chemistry
The Schrodinger equation:
ĤΨa=EaΨa
This equation describes the changes over time of a physical system in which quantum effects are significant and the wavefunction describes electronic position with respect to the nuclei. It can be used to determine the structure and properties of a molecule and hence can be used to describe the chemistry occurring in a system. The potential energy surface illustrates the energy of a system as a function of two or more coordinates and each point on a PES is associated with a different wavefunction. In order to utilise the WF, we must produce a mathematical representation that describes it as accurately as possible via LCAO and the use of basis sets which will be explored further.
Nf710 (talk) 21:29, 22 February 2018 (UTC) In your discussion youj have said wrt to time but you have given the time independent SE
Basis sets
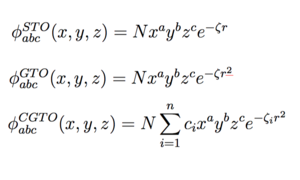
We utilize LCAO in order to build up a more detailed and comprehensive picture of the wavefunction. Basis sets are sets of atomic basis functions that can be combined to imitate MOs in LCAO to solve the Hamiltonian. A complete basis set can exactly represent any MO, however, these sets tend to contain an infinite number of functions and hence are not practical for calculations.
Slater functions are typically used to describe atomic orbitals however these prove to be difficult to integrate and would require a large amount of computing power. Therefore, in Gaussian, Gaussian functions are used as an alternative to Slater functions as they are far easier to handle mathematically. A single Gaussian function is called a 'primitive' Gaussian function however in practice, linear combinations of these functions are used called 'Contracted Gaussians' (see Figure 1). These CG's attempt to approximate Slater-type orbitals and Gaussian primitives are obtained via Hartree-Fock calculations whereby exponents are varied in order to achieve the lowest total potential energy.
A minimal basis set contains one Gaussian function for each AO in the atom to approximate the Slater-type orbital. However, in order to build a better picture of the wavefunction, extra atomic orbital basis functions are added which the Hartree-Fock method puts various weighting on to get a better description.1
Nf710 (talk) 21:33, 22 February 2018 (UTC) Nice!!!! This is a really good expanation. You have clearly done extra reading and understood it properly. You even included the equations.
Potential Energy Surfaces - Minima
A minimum on a PES can be defined as a point that has a first derivative equal to zero and a second derivative that is greater than zero (a positive value). This holds true for simple systems with only 2 degrees of freedom however for the more complex systems such as those studied here, more degrees of motion exist. A local minimum, of which there may be many, corresponds to several configurations that are similar and as such, all have similar energies. A global minimum, of which there is only one, corresponds to the true configuration that has the lowest energy.
For a molecule consisting of Natoms, 3Natoms - 6 degrees of freedom exist and hence the aforementioned derivative requirements for a minima, while still holding true, need further treatment in order to locate the true minima. This is due to the fact that our system can no longer be modelled as a simple harmonic oscillator and hence the force constant calculation is not as simple as just taking the second derivative of the energy.
The second derivative test uses concavity of a function at a critical point to determine whether it is a maximum or a minimum. A Hessian matrix can be used for the second derivative test if there are more than 2 variables (which is true for our system). A Hessian matrix contains the second-order partial derivatives of the energy of a molecule with respect to its geometry. Diagonalisation of this matrix produces the force constants of the system (eigenvalues of the matrix). At a true minimum, all force constants are positive and hence all molecular vibrations have a positive frequency. A higher force constant results in a higher frequency of molecular vibration. Throughout our analysis of the following systems, frequency calculations were run to ensure that all vibrations had a positive frequency at the proposed minimum.
Potential Energy Surfaces - Transition States
A transition state corresponds to the maximum on the minimum energy pathway for a reaction on a PES. This holds true for systems with only 2 degrees of freedom and in order to find the TS, a second derivative is taken at each point that has a first derivative of the energy equal to zero. A true TS point corresponding to a first derivative of zero will have positive second derivatives for all degrees of freedom except one. This negative second derivative results in a negative force constant and hence when frequency calculations were run, identification of a single negative frequency confirmed the location of a TS maxima.
However, for our more complication systems comprised of 3Natoms - 6 degrees of freedom, a Hessian matrix is again used in order to determine the force constants for the vibrations within our system (eigenvalues of the matrix).
Nf710 (talk) 21:40, 22 February 2018 (UTC) This is an excellent understanding well done. Almost correct, the eiegenvalues correspond to a eigenvector. the eigenvectors are linear combinations of the degrees of freedom and these are called the normal modes. thats why their vibrations look like bond forming/breaking because its all the degrees of freedom moving at the same time.
Computational Methods
Hartree Fock Method
The total potential energy of a molecule can be obtained by varying the coefficients during LCAO. The resulting one-electron wavefunctions describe the optimised molecular orbitals however the form of the wavefunction does not allow for instantaneous interactions between the electrons. Instead, the electrons feel the averaged field of all electrons present in the system. This is why the Hartree Fock method always overestimates the repulsion felt by an electron because it assumes it is feeling N electrons repulsion when instead it should be N-1 electrons repulsion as the electron cannot interact with itself.
Semi-empirical PM6 optimisation
The PM6 basis set was used for the majority of calculations in this lab. This method is based on the Hartree Fock model described above however it uses approximations and empirical data to reduce the processing power required to solve the Hamiltonian. This greatly reduces the time and cost of running such calculations on complex molecular systems.
Density Functional Theory (DFT) - B3LYP Optimisations
The higher level B3LYP optimisations used DFT to calculate the terms of the Hamiltonian. DFT calculates properties of a molecular system by using functionals. These functionals are functions of another function which is, in this case, the spatially dependent electron density. This method uses an effective potential that includes the external potential and Coulomb interactions between electrons (the exchange and correlation interactions). This makes this method much lower cost compared to the Hartree-Fock method which includes the electron correlation.
Fairly good understanding here, it would have been good if you could have included the equations. B3LYP is a hybrid methdo becuase it uses the DFT hamiltonian and the does a HF (and other stuff) in the exhange correlation functional to recover electron correlation.
Exercise 1
Exercise 1 entailed analysis of the pericyclic Diels-alder reaction between cis-Butadiene and Ethylene to produce cyclohexene as the product. Both cis-Butadiene and Ethylene were optimised to their minimum energy ground state using the semi-empirical PM6 method. The transition state underwent the same optimisation followed by a TS (berny) optimisation. An IRC was then run for the reaction.
Method 2 was used throughout the exercise and the bonds involved in the pericyclic reactions (end Cs of the diene and ethylene Cs) were frozen at a distance of 2.2 Å during ground state optimisation. The basis set used for optimisation throughout was PM6.
(Fv611 (talk) Excellent work throughout this section - very well done!)
Reaction Scheme
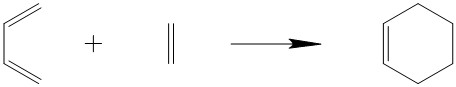
MO Analysis
Reactants
| HOMO | LUMO | |||||
|---|---|---|---|---|---|---|
| Butadiene | ||||||
| Ethylene |
Transition State
| HOMO-1 | HOMO | LUMO | LUMO+1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Transition State |
MO Diagram
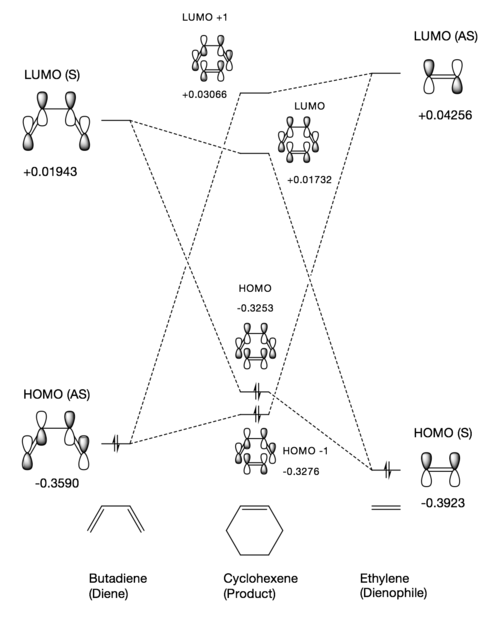
Following optimisation of the reactants and transition state, frontier MOs could be visualised in Gaussview along with their relative energies. The MO's and their corresponding energies can be seen in Figure 5 - an MO diagram to show the interaction between the reactants and the resulting transition state MOs.
Figure 5 shows that the HOMO of the diene is antisymmetric (AS) and the LUMO is symmetric (S). This is in contrast with ethylene where the HOMO is S and the LUMO is AS. The requirements for frontier MO interaction is that the MO's are of the same symmetry and they are close in energy. Orbitals interacting with the same symmetry have an overlap integral that is non-zero. Orbitals of opposite symmetry have an overlap integral equal to zero due to destructive interference cancelling out any constructive interference that might be occurring. As a result of this and as shown in Figure 5, the following interactions occur to produce the following TS MOs:
| Butadiene | Ethylene | Bonding interaction | Antibonding interaction |
|---|---|---|---|
| HOMO (AS) | LUMO (AS) | HOMO -1 | LUMO +1 |
| LUMO (S) | HOMO (S) | HOMO | LUMO |
As shown in the above table and in Figure 5, the HOMO of butadiene and LUMO of ethylene have interacted to form the TS HOMO -1 and LUMO +1. The HOMO of ethylene has also interacted with the LUMO of butadiene to form the HOMO and LUMO MOs of the transition state.
The HOMO -1 and LUMO +1 MO pair show greater splitting than the HOMO LUMO pair due to the fact that the frontier orbitals producing them are closer in energy and hence interact more strongly. The subsequent relative MO energies highlight the fact that this reaction is a normal electron demand Diels-Alder reaction as the diene is relatively electron rich compared to the dienophile, which is relatively electron poor. This is due to the fact that the dienophile MO's are lowered in energy whereas the diene MO's are raised in energy as a result of this strong interaction.
It can be further seen from Figure 5 that the resulting occupied TS MOs are actually higher in energy than the occupied frontier MOs that produced them. This overall increase in energy with respect to the reactants is expected as the transition state is defined as the maximum point along the minimum energy pathway. This difference in energy is represented by the activation energy of the reaction which is needed to reach the transition state.
Bond Length Analysis
| Butadiene | Ethylene | ||||
|---|---|---|---|---|---|
| Transition State | Cyclohexene | ||||
| C-C Hybridisation | Bond Length (nm) |
|---|---|
| sp3 - sp3 | 0.154 |
| sp3 - sp2 | 0.150 |
| sp2 - sp2 | 0.134 |
Shown above in Figure 6 are the bond lengths for the reactants, transition state and product for the Diels-Alder reaction between butadiene and ethylene. C-C bond lengths are also shown in Table 2 for various degrees of hybridisation. The Van der Waals radius for a carbon atom is 0.170 nm.3
The calculated C-C bond lengths of the reactants are in accordance with the aforementioned literature values. In the TS, C1-C4 in ethylene lengthens from 0.133 nm to 0.138 nm (C4-C5 in TS). This also occurs for C1-C2 and C3-C4 in butadiene. This is due to the fact that as the TS is formed, the double bonds present in these positions are breaking to form a sigma bond, giving a bond length that is just above the typical C=C distance.
C2-C3 in butadiene shortens from 0.147 nm to 0.141 nm in the TS (C1-C2 here). This is as a result of a double bond starting to form in this position and the bond length is starting to converge on the typical 0.134 nm C=C bond length.
The relative shortening and lengthening of these bonds are in accordance with TS theory which states that the transition state is an intermediate structure between the reactants and products. In the TS structure, C3-C4 and C5-C6 are 0.211 nm and 0.212 nm respectively. This distance is far shorter than 2 x typical VdW radius for a carbon atom which shows that their orbitals are interacting to form a new bond.
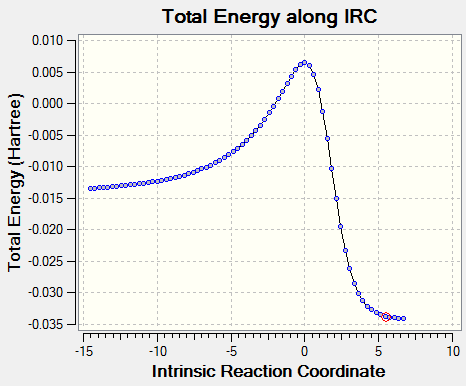
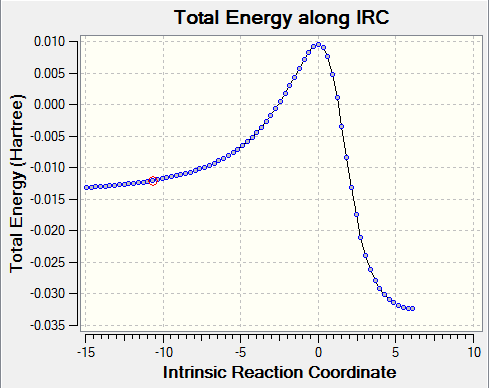
It is also worth comparing the relative differences between the bonds in the reactants, TS and products. Figure 7a below shows the calculated IRC for this reaction. It is clear from this plot that the TS is much closer in energy to the reactants than it is to the products, resulting in an early transition state. Early transition states resemble more closely the reactants rather than the products. This is in accordance with our calculated bond lengths as the double bonds that are breaking appear to closer in value (0.005 nm) to the reactant double bonds. This is compared to the C1-C2 distance in the TS (double bond that will form in the product) being further away in value (0.007 nm) compared to the C1-C2 distance in the product.


Transition State Vibration
As mentioned in the introduction, identification of a true TS can be confirmed by taking second derivatives at each point that has a first derivative of energy of zero. The resulting second derivatives will be positive in all degrees of freedom except one, which has a negative force constant. The vibration in this reaction corresponding to a negative force constant is shown above. The frequency of vibration is -948.57 cm-1 and is negative as a result of the negative force constant. The bond formation is clearly synchronous as the carbons involved in the reaction on butadiene and ethene approach each other in a concerted fashion.
Exercise 2
The following exercise involved calculations to find both the exo- and endo- product of the pericyclic reaction between 1,3-Dioxole and Cyclohexadiene. Method 2 was used throughout the experiment and initially, minimum energy calculations were performed on a guess TS using the PM6 and 6-31G(d) methods. Carbons involved in the reaction were set at distance of 2.2 Å and frozen for these optimisations. TS (berny) optimisations were then performed at both levels and finally, an IRC was taken at a PM6 optimisation level. The resulting product structure from the IRC was then used to perform a single point energy (SPE) calculation for both the reactants on the same PES so their relative energies could be quantitatively compared.
Reaction Scheme

MO Analysis
Reactants
| HOMO | LUMO | |||||
|---|---|---|---|---|---|---|
| Cyclohexadiene | ||||||
| 1,3-Dioxole |
Transition State
| HOMO (-1) | HOMO | LUMO | LUMO (+1) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Endo Product |
|
|
|
| ||||||||||||
| Exo Product |
|
|
|
|
The energies of the HOMO -1, HOMO, LUMO and LUMO +1 MOs for the exo and endo TS's in this reaction are shown in the figure above. A comparison of the TS MO energies reveals that the endo TS is more stable and thus has lower energy MO's. This is due to the fact that in the endo approach, the oxygen lone pairs can interact with the pi bonds in cyclohexadiene whereas this stabilisation is not possible in the exo TS. These secondary orbital interactions give an overall energy difference of ~0.005 Hartrees between the HOMO energies of the exo and endo TS's (see Figure 11).
MO Diagrams
(Fv611 (talk) Very good MO diagrams. You could have expanded the discussion by comparing the relative energies of the TS MOs in the endo and exo conformations.)


The same principles and requirements for frontier MO's to mix apply here as mentioned in exercise 1. The MO diagrams above were produced via analysis of the resulting MO's and their relative energies after the aforementioned optimisations. It is also noteworthy that the same frontier MOs are producing the same TS MO's as in exercise 1.
In order to determine whether this reaction is a normal or inverse electron demand Diels-Alder, a single point energy (SPE) calculation was run for the last point on the calculated IRC. This enabled quantitative analysis of the relative energies of the frontier molecular orbitals of 1,3-Dioxole and Cyclohexadiene. This calculation was required as in order to compare the energies quantitatively, both reactants had to be on the same PES. The frontier MO energies shown in the diagram were calculated for the reactants on different PES's which gives them different Hamiltonian potentials and hence they will have different relative energies. From the MO diagram, it can be seen that the strongest frontier MO interaction is between the HOMO of the dienophile and the LUMO of the diene which would suggest an inverse electron demand Diels-Alder. This was further confirmed by the SPE calculation that produced the following MO's in order of increasing energy:
| HOMO (-1) | HOMO | LUMO | LUMO (+1) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Endo Product |
|
|
|
| ||||||||||||
| Exo Product |
|
|
|
|
From the MOs generated in the SPE calculation, it is clear to see that the highest energy HOMO is that of the dienophile (1,3-Dioxole) which is typical of an inverse electron demand Diels-Alder reaction. This occurs for both the exo and endo transition states and, in this particular reaction, is a consequence of an electron rich dienolphile, 1,3-Dioxole, that contains electron donating oxygen heteroatoms. Electron donating groups (EDGs) raise the energy levels of the dienophile frontier MO's which causes them to be higher in energy overall compared to the diene. The same effects are also seen for an electron deficient diene (containing EWGs) which lowers the energy of the HOMO and LUMO. Here, lone pairs on the oxygen atoms of the dienophile are donating electron density into the alkene double bond which in turn raises the pi and pi* orbitals (HOMO and LUMO of dienophile respectively).
Nf710 (talk) 21:48, 22 February 2018 (UTC) Well done this is excellent.
Reaction Profile and Energy Calculations
| Reactants (kJ/mol) | Transition State (kJ/mol) | Product (kJ/mol) | Activation Barrier (kJ/mol) | Reaction Energy (kJ/mol) | |
|---|---|---|---|---|---|
| Endo | -1313782.01 | -1313622.16 | -1313849.37 | 159.85 | -67.36 |
| Exo | -1313782.01 | -1313614.33 | -1313845.77 | 167.68 | -63.76 |
The table above was obtained by optimisation and analysis of the reactants, TS and products. Minimum energy optimisations were run on the reactants separately and their energies added together. The TS energies were obtained using a TS (berny) calculation and product energies were produced by optimisation of the product structure from the IRC. All calculations were performed using the DFT-B3LYP method. The resulting reaction profile can be seen in the figure below:
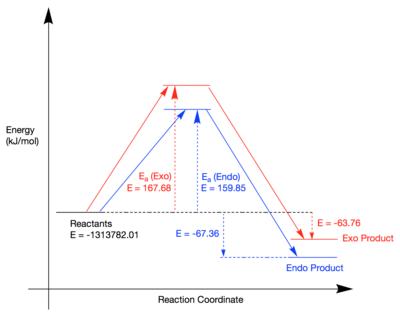
It is clear to see from the above diagram that the exo-TS has a higher energy compared to the endo-TS by +7.83 kJ/mol. The exo product is also higher in energy compared to the endo product by +3.6 kJ/mol. Therefore, the endo product is both the thermodynamic and kinetic product. Kinetically, the endo TS has a lower activation barrier due to the secondary orbital interactions mentioned in the MO analysis section of this exercise. The oxygen lone pairs on the 1,3-Dioxole can interact with the pi system on cyclohexadiene which stabilises the TS as can be seen in Figure 14. Such interaction is not possible in the exo TS. Thermodynamically, the endo product is lower in energy due to the fact that in the exo product, there is a steric clash between the H's on the dioxole and the carbon bridge as shown in the figure below:

The result of these relative energies is that the endo product will be the only product formed in this reaction.
Nf710 (talk) 21:53, 22 February 2018 (UTC) Excellent section, It could only have been improved if you had spoken about the thermodynamics/kentics of the reaction from a theoretical point of view.
Supporting Log Files
Endo product log file used to get energy:File:Ams1015ENDOPROD GS 631G.LOG
Exo product log file used to get energy:File:Ams1015EXOPROD GS 631G.LOG
Exercise 3
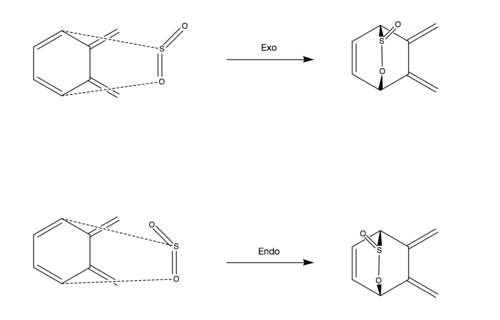
The following exercise involved analysis of both the exocyclic and endocyclic Diels-Alder reactions between o-Xylylene and Sulfur Dioxide. Method 3 was used throughout the exercise whereby the product was made and then optimised. Bonds between C-S and C-O were broken and frozen at a distance of 2.4 Å and 2.0 Å respectively and a minimum energy optimisation was calculated using the PM6 basis set. A TS(berny) and IRC were then run for all possible reaction pathways. A cheletropic alternative reaction was also analysed using the same method alongside the possible Diels-Alder pathways.
Reaction Scheme
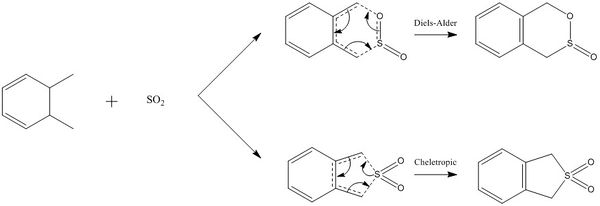
IRC Paths
| Reaction Type | IRC | Energy along the IRC |
|---|---|---|
| Endo-Diels-Alder | 
|
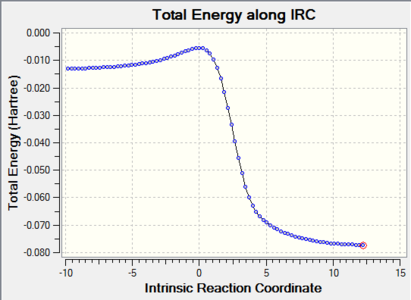
|
| Exo-Diels-Alder | 
|
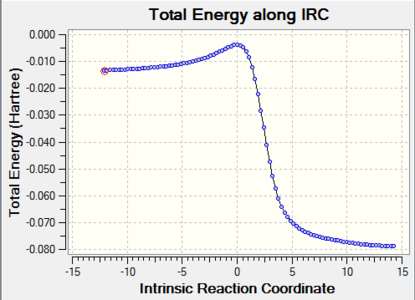
|
| Cheletropic | 
|
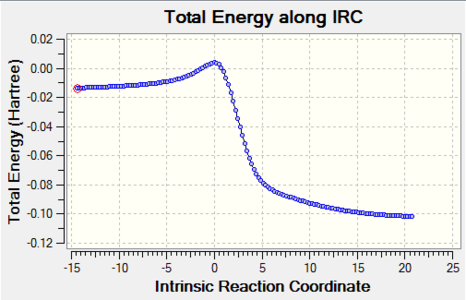
|
Reaction Energies and Coordinate
| Reactants (kJ/mol) | Transition State (kJ/mol) | Product (kJ/mol) | Activation Barrier (kJ/mol) | Reaction Energy (kJ/mol) | |
|---|---|---|---|---|---|
| Endo | 156.62 | 237.77 | 56.99 | 81.14 | -99.63 |
| Exo | 156.62 | 241.75 | 56.33 | 85.13 | -100.29 |
| Cheletropic | 156.62 | 260.08 | -0.01 | 103.46 | -156.63 |
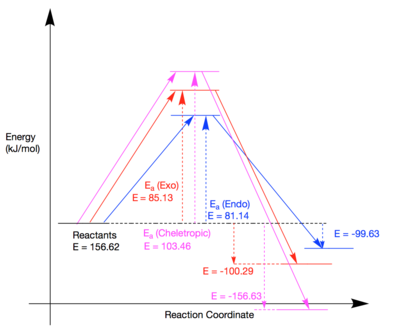
(This is good, but could do with some tidying. Also, you've already normalised with respect to the reactants, so you mustn't say here that the reactant energy is 156.62 kJ/mol, especially as you're declaring it the same kind of energy as the others. They are delta-energies and this is an absolute energy with a different reference point Tam10 (talk) 15:24, 26 February 2018 (UTC))
Shown above are the energies of the reactants, TSs and products for the reaction of o-Xylylene and SO2. A reaction profile also schematically highlights the different activation and reaction energies for the three available pathways.
It is clear to see that the endo TS has the lowest energy and hence is the kinetic product. Again, this could be due to a secondary orbital interaction between the lone pair on the oxygen in SO2 and the diene pi system. This interaction is not geometrically possible in either the exo- or cheletropic TS's. The most stable product is the cheletropic product. In all reactions, the aromaticity is restored in the fused 6-membered carbon ring. However, sulfur is a lot larger than carbon and hence the incorporation of a sulfur atom in a 6-membered ring in the exo and endo products will result in a large amount of ring strain. The cheletropic product forms a 5-membered ring with sulfur which would result in a much more sterically stable ring compared to a sulfur-containing 6-membered ring in the exo and endo products. This is visually represented in the videos in Figure 18 where it can be seen that after incorporation of a sulfur atom, the 6 membered ring is distorted whereas the 5 membered ring in the cheletropic product does not appear to suffer the same level of ring strain.
(There is also the retention of the strong S=O bond in the cheletropic product Tam10 (talk) 15:24, 26 February 2018 (UTC))
Alternative Endocyclic Reaction with Internal Diene
Reaction Scheme
A scheme for the alternative Diels-Alder reaction between o-Xylylene and SO2 can be seen above. This reaction was optimised using a PM6 basis set and the IRC was run at the same level.
IRC Paths
Energies
| Reactants (kJ/mol) | Transition State (kJ/mol) | Product (kJ/mol) | Activation Barrier (kJ/mol) | Reaction Energy (kJ/mol) | |
|---|---|---|---|---|---|
| Endo | 156.62 | 267.99 | 172.26 | 111.37 | +15.64 |
| Exo | 156.62 | 275.82 | 176.71 | 119.20 | +20.09 |
The above energies highlight the fact that these reactions are in fact endothermic and hence will not be thermodynamically favorable. The TS energies for both the alternative exo and endo reactions are higher than the corresponding exocyclic reactions with the terminal diene and hence these reactions will have a slower rate.
A potential reason for the TS's being higher in energy than the exocyclic reaction is that in the exocyclic reaction, the neighboring 6-membered ring benefits from restoration of aromaticity which will lower the overall energy of the TS's.
The overall result of these observations is that the endocyclic reaction will not occur in this system and instead all products will be as a result of the reaction with the external diene.
Supporting Log Files
Reactants:
Sulfur Dioxide File:Ams1015SO2 GS PM6.LOG
o-Xylylene File:Ams1015XYL GS PM6.LOG.
Exo-product (exocyclic):
Transition State File:Ams1015TRANSITION MIN TS PM6.LOG
Product File:Ams1015EX3 EXOPROD GS PM6.LOG.
Endo-product (exocyclic):
Transition State File:Ams1015endoTRANSITION MIN TS PM6.LOG
Product File:Ams1015EX3 ENDOPROD GS PM6.LOG.
Cheletropic:
Transition State File:Ams1015cheleTRANSITION TS PM6.LOG
Product File:Ams1015EX3 CHEPROD GS PM6.LOG.
Exo-product (endocyclic):
Transition State File:Ams1015ALTEXO MIN TS PM6.LOG
Product File:Ams1015EX3 ALTEXOPROD GS PM6.LOG.
Endo-product (endocyclic):
Transition State File:Ams1015altendoTRANSITION MIN TS PM6.LOG
Product File:Ams1015EX3 ALTENDOPROD GS PM6.LOG
IRC File:Ams1015ALTENDO IRC PM6.LOG
Extension - The ring closure of 1,3-Cyclooctadiene
The electrocyclic ring closure of 1,3-Cyclooctadiene was chosen as an extension activity. The 8-membered ring can undergo ring closure in the presence of PhLi. The resulting structure contains two fused 5-membered rings with only one alkene bond present.
Method 2 was used throughout the exercise. 1,3-Cyclooctadiene was optimised and the resulting structure was modified and re-optimised by removing one hydrogen and placing a lithium in the vicinity of the carbon holding the negative charge. The carbons involved in the ring closure were frozen at a distance of 2.2 Å and re-optimised to a minimum energy. A TS(berny) calculation enabled subsequent production of an IRC which can be seen in Figure 23.
Reaction Scheme
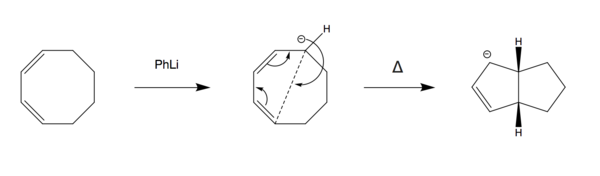
IRC movie
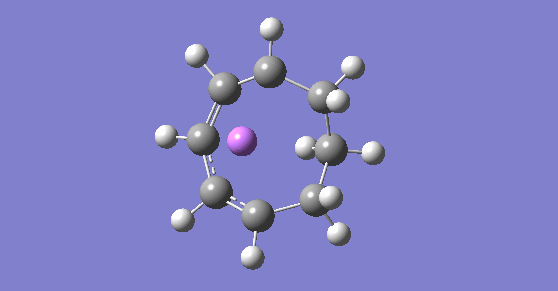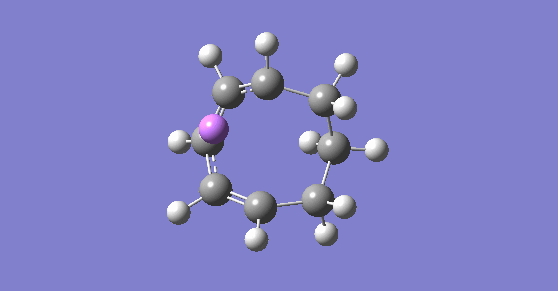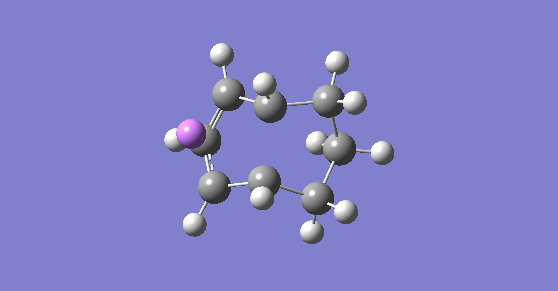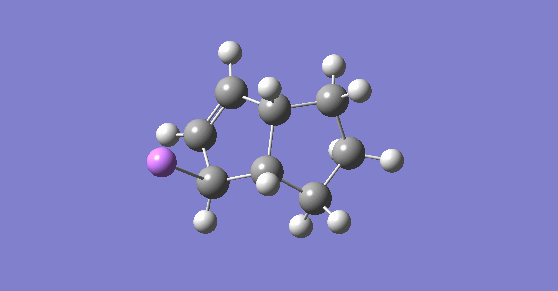
As shown in the figure above, throughout the reaction the Li ion travels around the ring to stabilise any negative charges forming as it acts as a counter ion to the carbanions. This suggests that the negative charge is delocalised around the ring in the middle structure of the reaction scheme and the Li ion follows this delocalised negative charge.
TS vibration
Again, location of a transition state was confirmed by only one negative frequency vibration occuring in the molecule (this vibration has a negative force constant). The frequency for this vibration was -600.72 cm-1 and can be seen in the figure below.
Reaction Energies
| Reactants (kJ/mol) | Transition State (kJ/mol) | Product (kJ/mol) | Activation Barrier (kJ/mol) | Reaction Energy (kJ/mol) |
|---|---|---|---|---|
| 432.57 | 614.50 | 414.90 | 181.93 | -17.67 |
After removal of a hydrogen by PhLi, the subsequent ring closure proceeded via an exothermic reaction as shown by the overall reaction energy of -17.67 kJ/mol. The product energy being lower than the reactant energy is likely due to the fact that Li is a hard cation and hence prefers to stabilise localised charges. In the negatively charged reactants, the negative charge is delocalised around the ring to a greater extent than in the products (the negative charge can be situated on three carbons in the reactants whereas it can only be situated on two in the products). The decreased extent of delocalisation in the product means that it can be stabilised more effectively by the hard Li cation compared to the reactants which results in a negative reaction energy.
Supporting Log Files
Reactants File:Ams1015REACTANTS LI GS PM6.LOG
Transition State File:Ams1015REACTANTS LI TS FREEZEBOND PM6.LOG
Product File:Ams1015FWPROD GS PM6.LOG
Conclusion
Three exercises were completed by monitoring different Diels-Alder reactions upon optimisation (at PM6 and/or B3LYP levels) of their reactants, transition states and products. Exercise 1 involved the reaction between cis-Butadiene and Ethylene which, upon analysis of the MO's, proved to be a normal electron demand Diels-Alder reaction. This was due to the fact that the dienophile's MO's were lowered in energy in the TS whereas the diene MO energy levels were raised. The requirements for frontier MO's to interact were proven here as it could be seen that only MO's of the same symmetry could interact to give a non-zero overlap integral. Bond length analysis highlighted an early TS due to the fact that the bond lengths present in the transition state more closely resembled the reactants rather than the products.
Exercise 2 again highlighted the requirements for MO interaction however, in this case, the reaction proceeded via an inverse electron demand Diels-Alder between 1,3-Dioxole and Cyclohexadiene. This was due to the fact that the dienophile in this reaction was electron rich due to the presence of oxygen's (EDG's) in the 1,3-Dioxole. This raised the energy of the dienophile frontier MO's and hence the strongest interaction occurring was between the HOMO of the dienophile and the LUMO of the diene. A single point energy calculation confirmed this as the relative MO energies of both reactants could be quantitatively compared and visualised. The endo product was confirmed to be both the thermodynamic and kinetic product.
Exercise 3 involved analysis of the reaction between Sulfur dioxide and o-Xylylene. Exocyclic, endocyclic and cheletropic reactions were optimised and compared. It was found that the overall kinetic product was the exocyclic endo product which was proposed to be as a consequence of secondary orbital interactions. The cheletropic product was the thermodynamic product due to a more stable 5-membered Sulfur containing ring being formed.
The electrocyclic ring closure of 1,3-Cyclooctadiene was studied as an extension. The IRC path highlighted the movement of a Li counter ion around the ring to stabilise any negatively charged carbanions being formed. The reaction was exothermic due to the fact that in the product, there is a lesser extent of delocalisation which can be better stabilised by the hard Li cation compared to the reactants.
References
1. V. Hänninen, presented as part of Introduction to Computational Chemistry, Finland, 25 September 2012
2. https://ocw.mit.edu/courses/chemistry/5-12-organic-chemistry-i-spring-2003/lecture-handouts/04.pdf
3. Bondi, A., Van der Waals Volumes and Radii, J. Phys. Chem., 1964, vol. 68, no. 3, pp. 441–451.