Rep:Mod:TS jx3515

Introduction

Potential Energy Surface (PES)

The concept of the potential energy surface (PES) comes from the relationship between the potential energy of a system and the change in any degree of freedom of the system, e.g. the bond length and angle, the movement of an atom in 3-dimensional space, the torsion of bonds, etc. In other words, the potential energy of a system can be changed by adjusting these parameters in order to reach a local or global minimum energy, i.e. a stable or meta-stable equilibrium. For example, using a 3-dimensional coordinate system, the potential energy is a function of the coordinates of every atom in x-, y- and z-axes respectively:

P E = V (x_{1}, y_{1}, z_{1}, x_{2}, y_{2}, z_{2}, . . ., x_{n}, y_{n}, z_{n})

Where $x_{n}$ , $y_{n}$ and $z_{n}$ means the x-, y- and z-coordinates of the n-th atom respectively.

However, in order to make use of the equation above, it should be assumed that the electron distribution is instantly changed with the movement of the nuclei, which is the Born-Oppenheimer approximation, for the interaction between the atoms is mostly contributed by the electron-electron interactions. By solving simplified single-electron Schrodinger equations plus dealing with the classical mechanics among nuclei, we can obtain an reasonable approximation of the energy of the system.

Nevertheless, It is difficult to visually illustrate the relationship between the degrees of freedom and the potential energy. Also, as for a specific reaction, not all of the parameters are interesting and crucial to the bond making for breaking. Actually, we can only focus on the parameters that can distinguish reactants and products by different values of this parameter, which are called order parameters. By selecting two appropriate order parameters as reaction coordinates, we can illustrate a potential energy surface in 3-dimensions, on which the height in z-axis of any point is dependent on the value of the two reaction coordinates in x- and y-axis. If the potential energy is plotted against only one reaction coordinate, the resultant diagram will be a curve called potential energy curve or profile.^[3]

The Minimum point and the Transition State

Analytically, The shape of the PES can be described by calculating the first and the second derivative of the potential function, which respectively describe the gradient and the curvature of a surface at a specific point.

The gradient describes the rate of change of the potential energy with changing reaction coordinates. If the gradient is not zero at a point, the system can lower its energy by changing its reaction coordinate towards the direction with lower energy. On the contrary, we could expect a system is in a equilibrium because it has no tendency towards any direction. In the simulation of a system, it can tell us the right direction of the optimization towards a minimum or maximum.

The curvature indicates the rate of change of the gradient. A greater curvature may result in a narrow potential well or a thin peak. The reason why the curvature is crucial in computational chemistry is that it directly relates to the force constant and the frequency of the oscillation in a potential well or a transition state. According to the Hooke's Law,

Nf710 (talk) 17:58, 22 February 2018 (UTC) This is a harmonic approximation

U (x) = \frac{1}{2} k x^{2}

,

the force constant $k$ is obtained by calculate the second derivative of the energy $U$ :

\frac{d^{2} U_{e l}}{d x^{2}} = k .

If the system is allow to oscillate on the surface of the potential well, the frequency of the oscillation $f$ is solely dependent on the force constant $k$ if the mass $m$ is fixed:

f = \frac{1}{2 π} \sqrt{\frac{k}{m}}

By calculating the curvature of the PES, we can identify whether a stationary point is a minimum, maximum or saddle point, also the properties of each oscillations, e.g. early or late transition state, stiffness of bonds, etc.

Normally, the reactant and product are located in a well of the PES, which have the lowest energy compared to the conformations in their neighborhood of the PES. If a minimum is located at $(x_{0}, y_{0})$ ,

\frac{\partial V}{\partial x} |_{x = x_{0}} = \frac{\partial V}{\partial y} |_{y = y_{0}} = 0

, and

\frac{\partial^{2} V}{\partial x^{2}} |_{x = x_{0}} > 0

and

\frac{\partial^{2} V}{\partial y^{2}} |_{y = y_{0}} > 0

.

The expressions above indicates that the potential energy will always increase no matter in which direction a system is disturbed from a minimum. In other words, it is impossible for a system to escape from the potential well if no extra energy is added.

Therefore, an energy barrier needs to be overcome in order to transform the system from one potential minimum to another. The point with the maximum energy on the reaction route is called a transition state. The first derivatives of the transition state are also zero, but the second derivatives are not positive in all directions anymore. The transition state is a minimum in one direction (which is mostly the direction connecting two adjacent potential wells) but a maximum in another direction orthogonal to the previous one, which is called a saddle point. By this special property of the transition state, its height indicates the minimum energy needed to overcome the maximum potential in the ideal reaction route. In the computations, the transition state can be found by inspecting a negative frequency of oscillation, because it is an inversion of a potential well which has a real oscillation frequency, whereas the maximum does not have such a real oscillation but we can extract a imaginary frequency with respect to its curvature.

Nf710 (talk) 18:05, 22 February 2018 (UTC)You are correct in 2 dimensions but you need to talk in 3N-6 dimensions. the curvature for each of the normal modes is given by diagonalising the hessian matrix. the eigen values are the curvature and the eigenvectors are the normal modes. these are the 3N-6 degrees of freedom linearly combined. moving back and forward along these eigenvectors in the vibration that you see.

In this experiment, the transition state of several bimolecular reactions has been found using Gaussian,^[4] which is a software solving the Schrodinger equations to research the energy profiles of molecular systems. The calculations were carried out using different algorithms e.g. PM6 or B3LYP/6-31Gd with different precision. The results of computations gave good explanations to chemoselectivity and regioselectivity of several Diels-Alder reactions and competitive reactions.

Nf710 (talk) 18:05, 22 February 2018 (UTC) You shoudl have spoken abit about the quantum chemical methods used in the lab.

Exercise 1: The Diels-Alder Reaction

Frontier Molecular Orbitals

Butadiene

Ethene

Transition State of Cyclohexene Formation

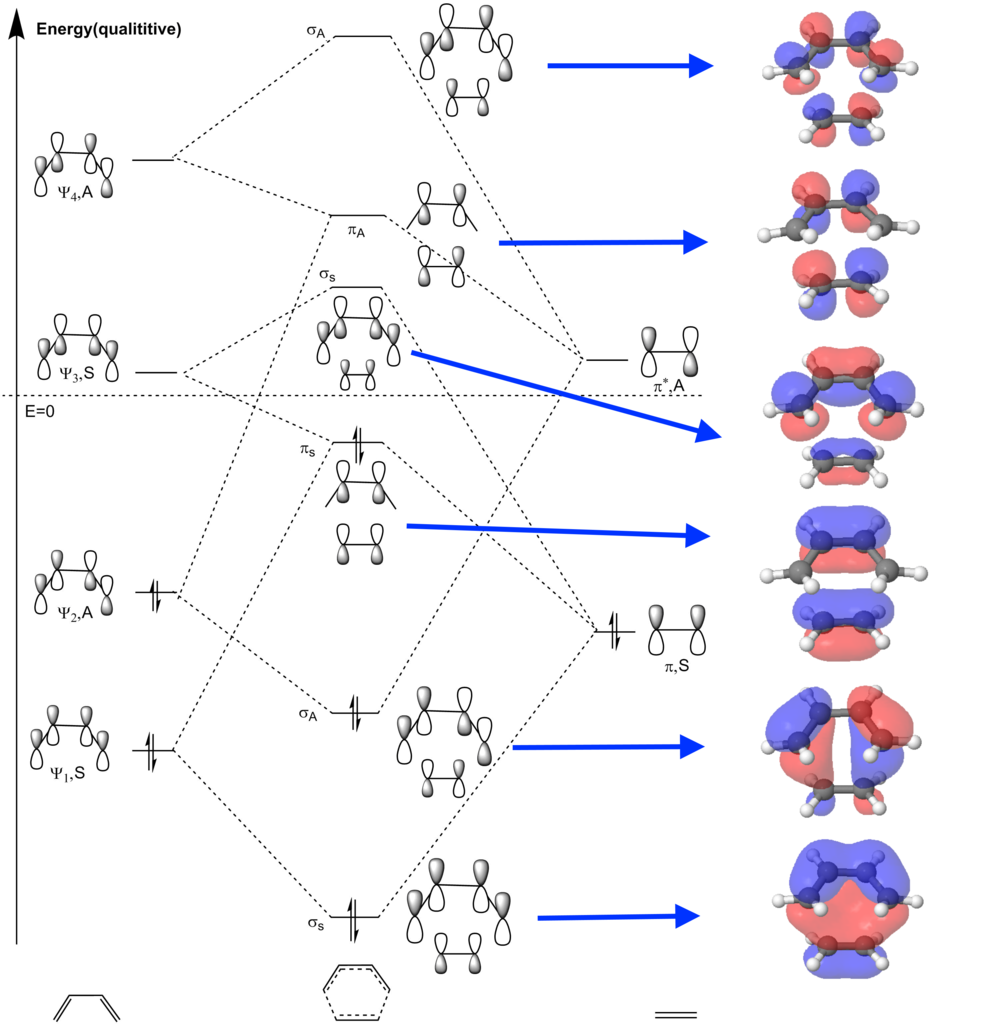
MO Diagrams for the Frontier Orbitals

(Fv611 (talk) Your MO diagram and following discussion are incorrect: there is a lot of confusion here. Firstly, there are only 2 frontier orbitals per reactant. Additionally, you have used the formula (2 x frontier MOs) x (2 x labels) x (2 x type of combination) to calculate the number of expected frontier MOs for the transition state. In reality, you have to consider two possible combination per pair of allowed interactions between the frontier FMOs of the reactants. In this case, only the interactions between the butadiene HOMO and the ethene LUMO, and those between the ethene HOMO and the butadiene LUMO, are allowed. As each interaction produces one bonding and one antibonding orbital, we expect 4 frontier TS MOs. You have not recognized that the butadiene's HOMO-1 and LUMO+1 are not close enough in energy to interact with the ethene's frontier orbitals and are therefore not involved in the bonding. You are also drawing the TS's HOMO and LUMO +1 as a result of the combination of 4 orbitals, which is impossible.)

Discussion

1. MO Symmetry of the Transition State

According to the MO diagram, it can be easily found that only the orbitals with the same symmetry labels can give a non-zero integral when overlapping with each other, i.e. symmetric-symmetric orbitals and antisymmetric-antisymmetric orbitals. Contrarily, the overlap between the orbitals with different labels (i.e. symmetric-antisymmetric orbitals) will give a overall zero integral, which means the overlap of the wavefunctions cannot give electron density at the bond to be formed. Therefore, by mixing up the orbitals with the same label, 6 resultant MOs of the transition state (TS) may be obtained because we originally have 6 frontier MOs from butadiene and ethene.

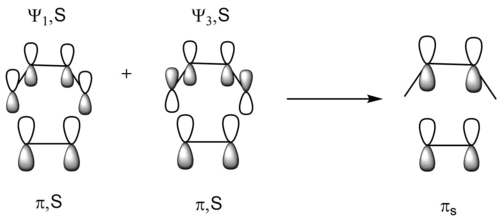
If we simply inspect the 6 frontier MOs from butadiene and ethene, actually we can obtain 8 combinations of resualtant MOs, as 2 (types of labels) × 2 (MOs from butadiene in each type) × 2 (bonding or antibonding) = 8. However, it is obviously impossible to form 8 TS MOs, for there are only 6 frontier MOs for the input. Instead, there are two π-symmetry orbitals which could be regarded as a mixing of two combinations of frontier MOs. Also, the position of the lobes of the π_s orbital is exactly where the new π-bond is forming and the π-bond of ethene is breaking, so it give an good illustration of the electron distribution during the transition state.

Due to the fact that only the MOs with the same symmetry label can interact, we could expect that the labels of occupied and unoccupied frontier MOs have to remain unchanged at the transition state. In other words, the electrons from an symmetric orbital of reactants have to stay in an symmetric orbital in the TS MOs as well, and so do antisymmetric orbitals. Therefore, the number of occupied and unoccupied symmetric and antisymmetric MOs respectively has to be the same. For this [4+2]-cycloaddition, there are two symmetric MOs and one antisymmetric MO for the frontier MOs as well as the TS MOs. The overall energy for the TS does not show a dramatic increase for the MO interaction. Instead, there is even some stabilisation for the interaction between the two symmetric bonding orbitals of the reactants (i.e. Ψ₁ of butadiene and π of ethene). The HOMO of TS MOs is generated by the attacking from the HOMO of ethene to the LUMO of butadiene, storing the electrons from symmetric orbitals at a relatively low energy, which is totally thermally accessible. Therefore, we can deduce that the requirement for an allowed reaction is that the low-lying MOs of the TS must have the same symmetry with the bonding MOs of reactants, so that there would be no great energy barrier for the transformation of the orbitals.

The method and predicting the availability of pericyclic reactions by inspecting π-electrons is also known as the Woodward-Hoffmann rules. It points out that molecular orbitals transformations over the course of the reaction must conserve the symmetry of the molecular orbitals. According to this, it deduces that a thermally allowed suprafacial/suprafacial cycloaddition requires p + q = 4n + 2, where p and q are the number of π-electrons from two reactants respectively, and n is any integer. This rule is totally consistent with the calculations of this TS of cycloaddition.^[5]

2.Behaviours at the Transition State

As the vibrational mode above shows, the formation of the two bonds are synchronous, for the two ends of reactants approaches simultaneously. This also demonstrates that the frontier MOs have the right symmetry to form the bonds.

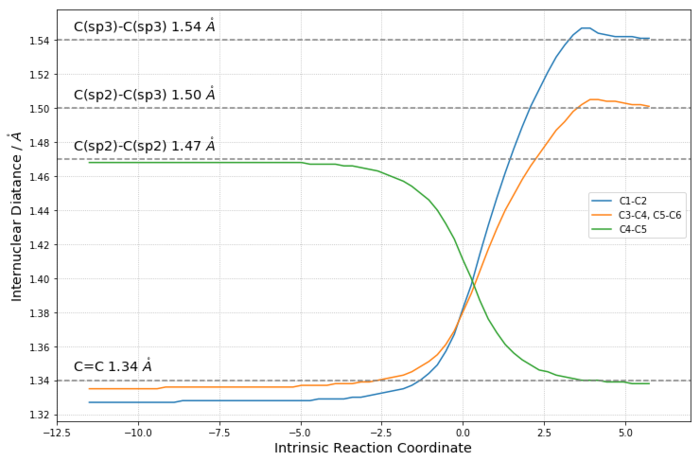
Over the course of the reaction, there are three C-C π-bonds breaking, one C-C π-bond and two C-C σ-bonds forming. Therefore, we can expect that the breakage of the π-bonds would lengthen the bonds and the formation shorten the bond, and at the transition state the bond lengths would be in between the typical lengths of single and double bonds.

In order to check the confidence of the calculation, a plot of the internuclear distance has been made as on the right. When the distance between two ends of the alkenes is smaller than twice of the VdW radius of carbon (~ 3.4 Å), the reaction begins and the overall energy increases. As they approach each other to 1.5 times the VdW radius, the bond lengths start changing dramatically, and the greatest slope occurs at roughly the transition state, which is the point where the energy reaches a maximum. All bond lengths are in the middle of single and double bond at this moment. After that, the overall energy decreases and the two σ-bonds are formed between the ends of alkenes.

The bond lengths calculated all have a good consistency with the typical lengths of C-C bonds, which means the TS simulation is reliable and successful.

Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole

Frontier Molecular Orbitals

Cyclohexadiene

1,3-Dioxole

Exo Transition state

Endo Transition state

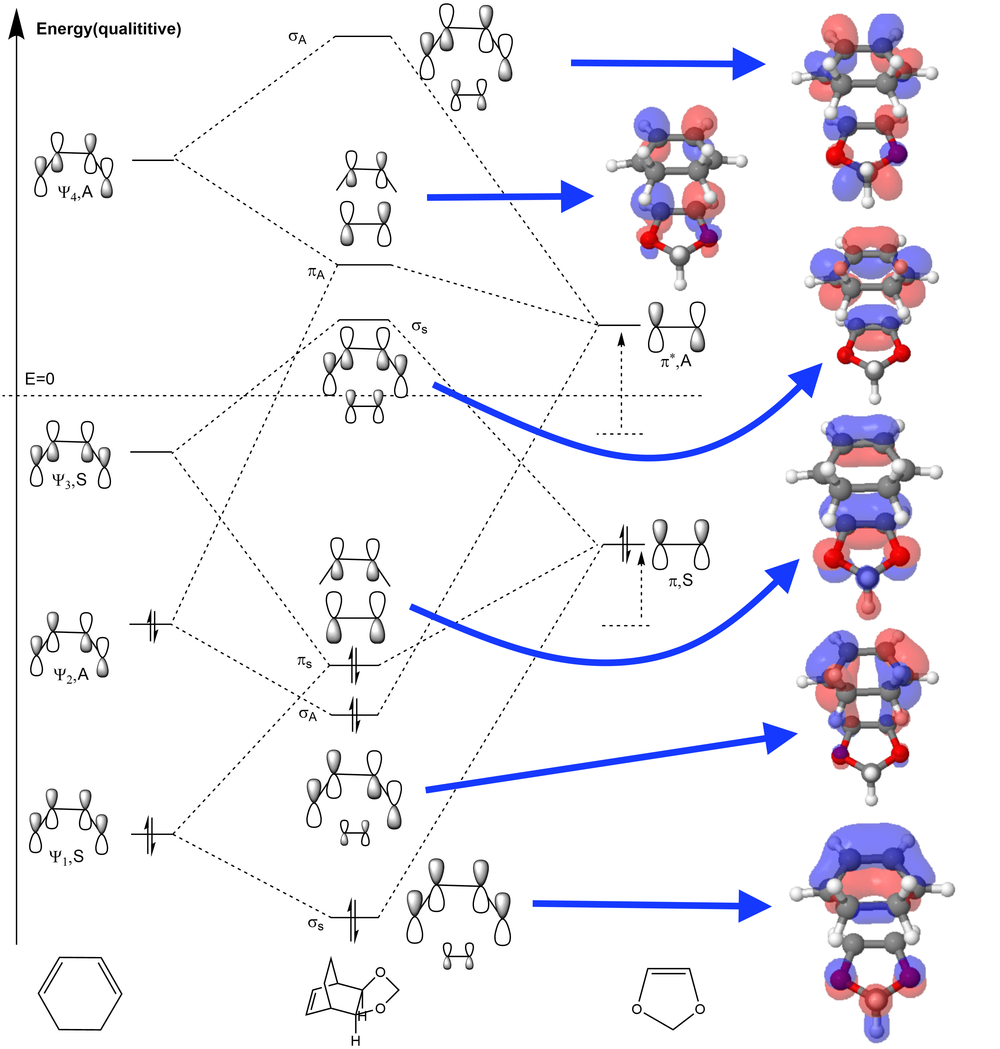
MO Diagram for the Frontier Orbitals

(Fv611 (talk) Again, your diagram is incorrect (same confusions as in exercise 1). I recommend you read up on your second year MO course to refresh your memory.)

Characteristic Energy of the Reaction

Species	Cyclohexadiene	1,3-Dioxole	Exo Product	Endo Product
Gibbs Free Energy	-233.324376 hartrees	-267.068641 hartrees	-500.417306 hartrees	-500.418694 hartrees
Transition State Free Energy	-	-	-500.329163 hartrees	-500.332151 hartrees
Activation Energy (ΔG^‡)	-	-	0.063854 hartrees = 167.6 kJ/mol	0.060866 hartrees = 159.8 kJ/mol
Reaction Energy (ΔG)	-	-	-0.024289 hartrees = -63.8 kJ/mol	-0.025677 hartrees = -67.4 KJ/mol

Discussion

1. Influence of the use of 1,3-dioxole

Compared to Exercise 1, the ethene is replaced by 1,3-dioxole, in which two oxygen atoms directly connect to the alkene. The participation of the oxygen atoms changes the energy level of the frontier MOs of alkene, for oxygen can behave as an electron donating group and make the alkene relatively electron-rich. As a result, the energy levels of HOMO and LUMO become relatively higher than those of unsubstituted simple conjugated alkene or ethene, so that the HOMO of the dioxole is closer in energy to the LUMO of the cyclohexadiene and they can mix to a greater extent to form a more stabilized orbital. This change is illustrated in the MO diagram above, in which the elevated energy level on the right is indicated by the dashed lines (representing the orbitals of ethene) and arrows (representing the effect of participation of oxygen atom).

This adjustment to dienophile promotes the inverse electron-demand Diels-Alder reaction. In a typical inverse demand D-A reaction, the dienophile is substituted with an electron-donating group to make it electron-rich, and the diene contains an electron-withdrawing group to make it electron-poor. Therefore, the HOMO/LUMO of dienophile is elevated and those of diene is lowered, so that the LUMO of dienophile and the HOMO of diene is closer in energy, which promotes the interaction between these two orbitals and decreases the energy barrier of bond formation, also results in a more stabilized HOMO of the product. Contrarily, the normal demand of D-A reaction requires an electron-withdrawing group attached on the dienophile and an electron-donating group attached to the diene, which results in closer energy levels of HOMO of diene and LUMO of dienophile. However, the inverse damand D-A reaction usually involves heteroatoms, so it is often used for the formation of heterocycles.

In this inverse electron-demand D-A reaction, although the dienophile is electron-rich due to the oxygen atoms, the diene is not adjusted to become more electron-poor, so the inverse-electron demand is not maximised. Nevertheless, this energy gap is already much smaller than that between butadiene and ethene if simply inspecting the MO energy (~0.18 hartrees for 1,3-dioxole and cyclohexadiene vs. ~0.24 hartrees for ethene and butadiene (B3LYP/631Gd)). Therefore, it can be expected that this reaction would have a faster reaction rate and a good stabilization of the product.

Nf710 (talk) This observation is correct if you have done the single point energy on the reactants in the irc. (on the same potential surface) I don't know if you have because you have just stated values. Furthermore you observation about the electron demand can be tested quantitatively if you have run the single point energy calculation. Therefore giving you a numerical value of how close the MOs are in relation to each other.

2. Selectivity of endo and exo products

In this reaction, the dienophile is no longer a totally symmetric species, and it is expected to show a stereoselectivity depending on the direction of dienophile while cycloaddition. The major and minor products can be predicted by the energy of the transition state and the products. According to the Gibbs free energies calculated by Gaussian which are tabulated above, the endo isomer has both the lowest energy at the transition state and at the stage of product, which means the endo product is both kinetically and thermodynamically favoured. Generally, it is found that the endo isomer is often the major product, for the reaction is under kinetic control at ambient temperature. Therefore it could be expected that under relatively low temperature, the endo product would be the major product. Regarding that the energy difference between the two TS is not very large (~7.8 kJ/mol), the selectivity would not be extreme. If the reaction is equilibrated under high temperature for a long time, the endo isomer would be still the major product but the major/minor ratio might decrease, because the energy difference between the two product is smaller than that of the TS (~3.6 kJ/mol vs. 7.8 kJ/mol).

The reason for the lower energy of the TS of endo product can be explained by the frontier molecular orbital theory. The theory summarized that the interaction between occupied MOs of one molecule and unoccupied MOs in the other molecule makes them attract to each other. This is the most useful when inspecting frontier MOs like HOMO and LUMO to predict their stereoselectivity, as some non-bonding MO interactions between reactants could lower the TS energy and drive the molecules to favoured positions, which is called the secondary orbital interactions. According to the illustration of the HOMO of TS below, there is a secondary orbital interaction between the oxygen atoms and the LUMO of cyclohexadiene. Although it could be expected that the endo-position would has more chance to suffer from steric repulsion, the attraction due to secondary orbital effect could be the dominant factor.^[6]

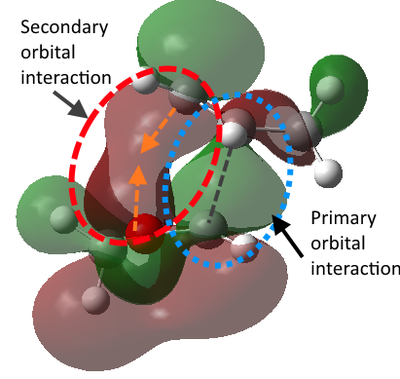
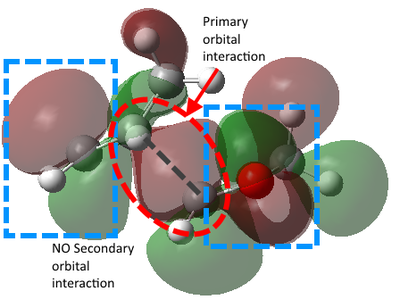
Nf710 (talk) 18:12, 22 February 2018 (UTC) These diagrams are very nice and you have written the section very nicely. you have got the correct energies and you have come to the correct conclusions but there were a few things that you missed out/ could have gone into more detail with.

Exercise 3: Diels-Alder vs Cheletropic

Frontier Molecular Orbitals

Products

Exo Product

Endo Product

Cheletropic Product

TS

Product

IRC

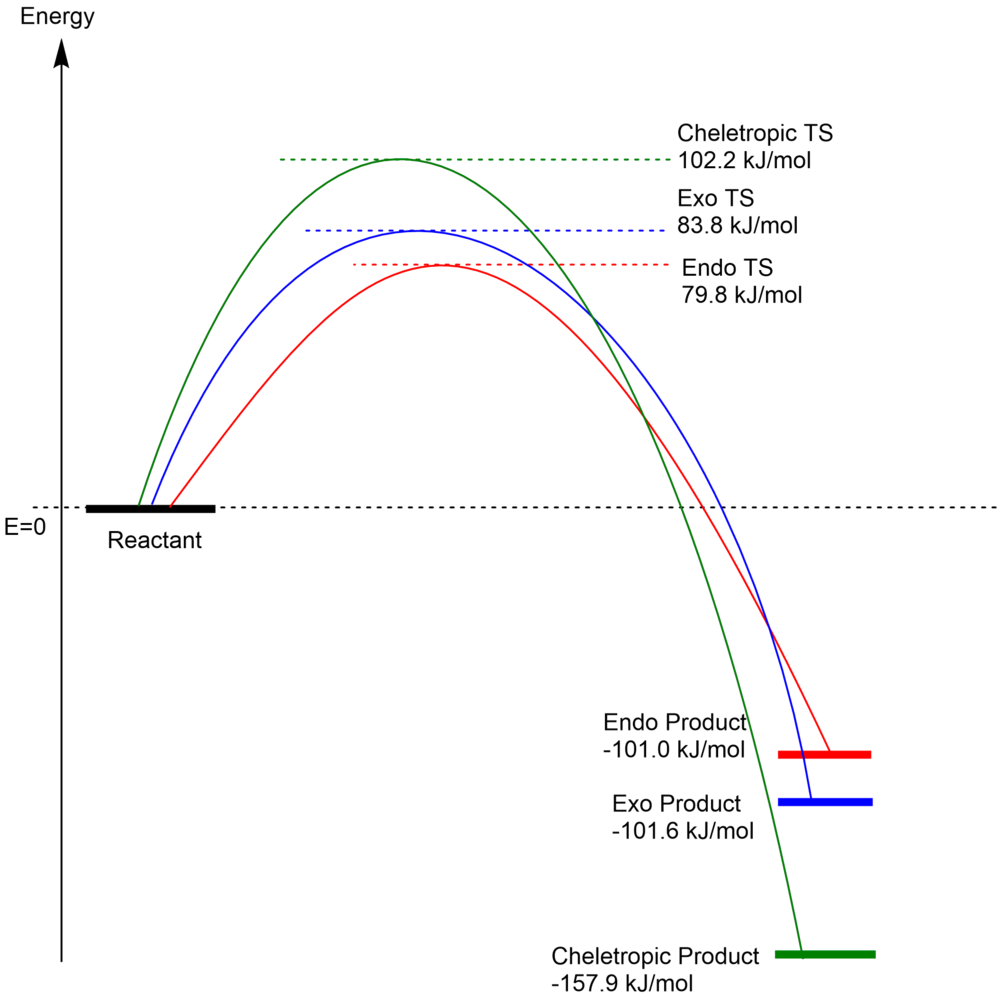
Characteristic Energy of the Reactions

Species	Xylylene	Sulfur Dioxide	Exo Product	Endo Product	Cheletropic Product
Gibbs Free Energy (Hartrees)	0.178764	-0.118614	0.021453	0.021697	-0.000002
Transition State Free Energy (Hartrees)	-	-	0.092076	0.090560	0.099063
Activation Energy (ΔG^‡)	-	-	0.031926 hartrees = 83.8 kJ/mol	0.03041 hartrees = 79.8 kJ/mol	0.038913 hartrees = 102.2 kJ/mol
Reaction Energy (ΔG)	-	-	-0.038697 hartrees = -101.6 kJ/mol	-0.038453 hartrees = -101.0 KJ/mol	-0.060152 hartrees = -157.9 kJ/mol

(Your xylylene energy is a bit too high Tam10 (talk) 14:47, 26 February 2018 (UTC))

(Don't use curved lines for energy profiles like this - straight lines between the stationary points is easier to read. Tam10 (talk) 14:47, 26 February 2018 (UTC))

Discussion

1. Selectivity of Products

In this reaction, there are three routes directing to different products. The reactants can undergo cycloaddition to form endo or exo products with S and O atoms, or undergo cheletropic reaction to form a 5-membered ring with solely the S atom. According to the energies from the calculation, the endo product has the lowest energy at the transition state, so it could be the kinetic product, and it is expected to yield the most under kinetic control (relatively low temperature). As the energy difference between the exo TS and the endo TS is not very large, the endo/exo ratio would not be extreme. However, the energy for cheletropic TS is much higher, so it would be not reachable under kinetic control. On the other hand, if the reaction is allowed to equilibrate for a long time under high temperature (i.e. thermodynamic control), the major product would be the cheletropic one, as it has the lowest energy for products, and the major/minor product ratio would be very large due to the energy difference of greater than 50 kJ/mol.

2. Bond Change of Xylylene

Xylylene has 8 π-electrons but does not have aromaticity. The π-bonds in xylylene are only conjugated but cannot form a delocalised system without transfer of electrons. Hence, the double bonds and single bonds in xylylene show a typical difference in bond lengths (~1.35 Å for double bonds vs. ~1.46 Å for single bonds). After the reaction, a delocalised π-system is formed and the 6-membered ring becomes a benzene ring. As a result, the six bonds in the ring become identical, and the bond length is in between a single bond and a double bond (~1.40 Å).

("... but does not have aromaticity" - 8π systems are not aromatic anyway Tam10 (talk) 14:47, 26 February 2018 (UTC))

3. Another Reaction Site

There is a second available butadiene fragment located in the 6-membered ring, and both endo and exo products at this site are also optimized by directly building the final products.

However, their free energy is even higher than the sum of the reactants (0.06015 hartrees). It means the reactions via the two routes needs additional energy, so these reactions are thermodynamically unlikely to happen. In addition, the activation energy is approximately three times larger than other routes, which means these are highly kinetically unfavoured. As a result, these two products are not expected to be observed in a real reaction.

Conclusion

By calculating electron configuration using Gaussian, the structure of reactants and products of three Diels-Alder reactions has been optimized and their transition state has been located. It was found that the [4+2]-cycloaddition applies suprafacial orbital interactions, and it is proved by inspecting the frontier MOs at the transition state. The MO diagrams for normal and inverse demand Diels-Alder reaction was also built based on the frontier MOs calculated. It was found that by substituting the dienophile with electron donating groups the reaction turns inverse electron-demand and the energy gap between the HOMO of dienophile and the LUMO of diene becomes smaller, which is helpful to lower the energy of transition state and promote the cycloaddition. It was also found that the secondary orbital interaction plays an important role in the transition state of the endo product, which helps to stabilize the HOMO of the transition state and lowers the energy barrier of the reaction. As a result, the endo product is the major component in the product under kinetic control. However, if SO₂ is used as dienophile, there is a possibility to yield cheletropic product under thermodynamic control. The methods used in this experiment is mainly PM6 but B3LYP/631G(d) was also used for more precise calculation. In spite of lower reliability of PM6 than the DFT method due to its semi-empirical nature, it can provide a much faster and more convenient estimation with reasonable accuracy, which is particularly useful before more precise calculation.

Reference

1. Potential Energy Surface [Internet]. Chemistry LibreTexts. 2017 [cited 2018 Feb 13]. Available from: https://chem.libretexts.org/Core/Physical_and_Theoretical_Chemistry/Quantum_Mechanics/11%3A_Molecules/Potential_Energy_Surface

2. Principal curvature. In: Wikipedia [Internet]. 2018. Available from: https://en.wikipedia.org/w/index.php?title=Principal_curvature&oldid=823522725

3. Wales D. Energy Landscapes: Applications to Clusters, Biomolecules and Glasses. Cambridge University Press; 2003. 696 p.

4. Gaussian 09, Revision D.01, M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, and D. J. Fox, Gaussian, Inc., Wallingford CT, 2016.

5. Clayden J, Greeves N, Warren S. Organic Chemistry. OUP Oxford; 2012. 1262 p.

6. Fleming I. Frontier Orbitals and Organic Chemical Reactions. Wiley; 1976. 249 p.