Rep:Mod:TSYts15

Introduction

To begin with, Optimisation and Frequency calculation are particularly fundamental at Computational Chemistry. These calculation provide important insight to kinetic and thermodynamic parameters in a chemical reaction.

A Potential Energy Surface (PES) is illustrated below.

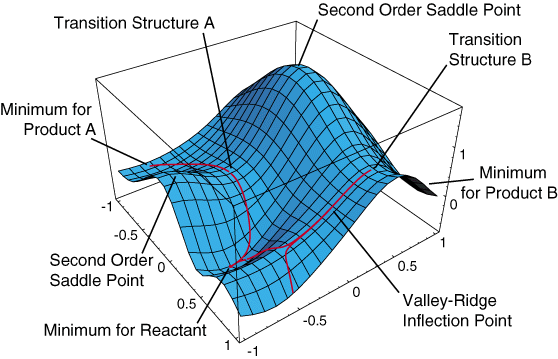
The minima are represented by A and B which corresponds to reactants and products. Hence ,the reaction path is defined between the two minima. From the PES, reactants pass through the activation barrier, the peak of energy profile (first order saddle point), along the reaction path. Hence, a transition state is the first order saddle point on a PES. The vibration calculation of a transition state demonstrates one negative frequency which indicates a negative force constant. This means that energy is at maximum in only one direction of nuclear-configuration space. While the energy is remain minimum in all other orthogonal directions. Therefore, it is necessary to verify the correct TS by performing frequency calculation plus geometry optimisation at the same computation basis set in this exercise. The imaginary frequency corresponds to the translational motion of transformation from reactants to products.

These can be quantified by mathematical concept as shown in Intro: Table 1 Gradient and curvature at mimimum and transition state.

Nf710 (talk) 21:54, 29 November 2017 (UTC) Firstly in Guassian we workin in the space of the 3N-6 degrees of freedom and these are the coorodinates to which we find the forst constants. (its is actually he normal modes which is 3n-6 of these degrees of freedom)

Intro: Table 1 Gradient and curvature at mimimum and transition state

	Minimum	Transition state
Gradient	$\frac{\partial V}{\partial (r_i)}=0$
curvature	$\frac{{\partial }^{2}V}{\partial (r_1{)}^2}>0$	$\frac{{\partial }^{2}V}{\partial (r_1{)}^2}<0$

In addition, frequencies allow calculation on the second derivatives of the optimised system three-dimentional matrix. The calculated second derivatives give the force constants (formula 1). As a result, frequency can be calculated from the force constant (formula 2)

Nf710 (talk) 21:54, 29 November 2017 (UTC) I dont know what you mean by the optimised 3 dimensional matrix

$k=\frac{{\partial }^{2}E}{\partial q^2}$
Formula 1. Force Constant

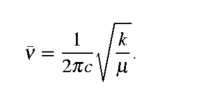
v is frequency , c, the speed of light, the force constant, and μ the reduced mass
Formula 2. Frequency Calculation

Moreover, both basis set of PM6 and B3LYP were used to provide optimisation result. Hatree-Fock, B3LYP method has a great advantage on treating electron correlation quite well whereas this is not the case for basis set PM6. Electron correlation is particularly relevant to transition state calculations and hence, providing a more accurate calculation. As a result, in exercise 2, B3LYP method is used in addition to PM6 method. Using PM6 basis set alone may yield incorrect prediction of the reaction. In contrast, semiempirical method, PM6 is an approximate verision of Hatree-Fock which reduce computation effort significantly at the expenses of accuracy. Only valence electrons are considered and a minimum basis set is used for the calculation. Semiempirical method, PM6, eliminates some two-electron or one-electron integral and insert empirical parameters to make up the neglected integral. As a result, Semiempirical PM 6 is well peformed in Exercise 1 and 3 since previous experimental data is available to correlate with. Another advantage of PM6 Basis set is Quantum Mechanics based calculation which is more robust than force fields.

Nf710 (talk) 21:54, 29 November 2017 (UTC) OK PM6 is correct, well done. good understanding there. B3LYP is a DFT method which used also a HF method to calculate the electron correlation. So techically it is a hybrid method.

Exercise 1: Reaction of Butadiene with Ethylene

Fig. 1: Reaction Scheme of Butadiene with Ethylene in Exercise 1

Optimization Result

Table 1. Optimization Result of Reactant, TS and Products at PM6 Basics Set

Butadiene	Ethylene	Transition States	Product

The Table 1 shows the result of optimisation of reactants, TS and product at PM6 level respectively. Correct TS was further confirmed by frequency calculation and IRC.

Frequency

Fig. 2: Frequency Calculation of TS

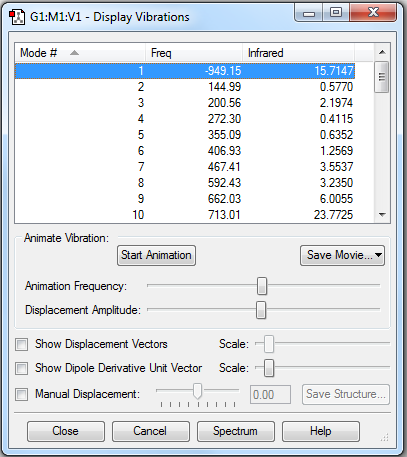
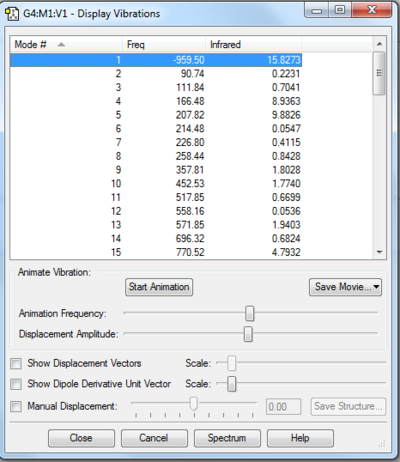
From Fig. 2, a negative frequency is shown in the final optimised TS. This indicates imaginary vibrational frequency associated with a TS which corresponds to the translational motion of carbon. At Gaussian, second derivative of the energy with respect to the nuclear position is calculated by the frequency. Hence, the first negative frequency indicates one negative second derivation, which confirms a transition state (the highest point on the minimum energy path linking the reactants and products). High frequency, greater than |100^-1|, is consistent with this kind of molecule. As a result, this represents a correct TS is obtained from final optimisation . Additionally, this plays an important part in defining chemical reactions. One negative frequency also indicates the presence of single TS which illustrates a well-defined reaction profile and complete reaction.

IRC

Fig. 3: IRC

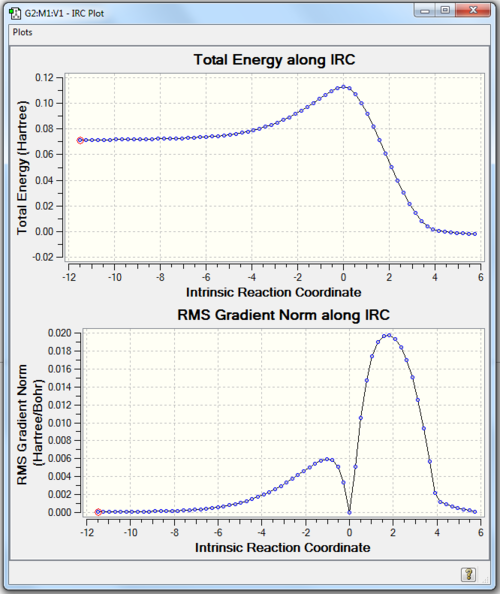
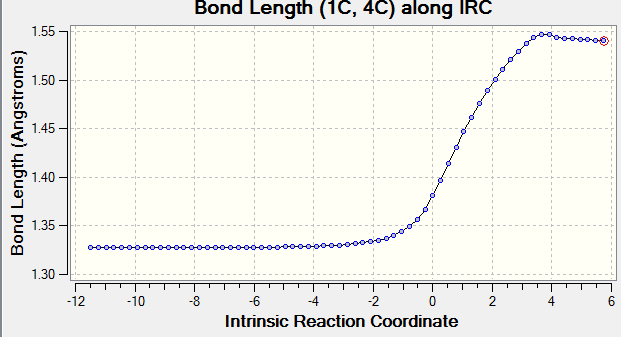
Transition state geometries can be connected to ground state geometries with an Intrinsic Reaction Coordination calculation (IRC) performed by Gaussian. In Fig 3., the downhill path from the transition is followed in forward direction. A well defined and asymmetric Free Energy Surface as shown in Fig. 3 confirms that TS is correctly optimised.

MO Analysis

MO diagram for the formation of butadiene/ethene TS is illustrated in Fig. 4 MO Diagram for the formation of Butadiene/ Ethene. It is correlated with the actual MOs are performed by Gaussian at Basis Set PM6. It is shown that TS LUMO +1 has energy lower than expected (stabilisation) and TS HOMO has energy higher than expected (destabilisation). Hence, this suggested that there is significant mixing between orbitals. In addition, it is important to note that the splitting between HOMO and LUMO of Butadiene (Diene) is much smaller than that of Ethene (Dienophile). This can be explained by the extra stabilisation of the conjugated system in Butadiene. From the MO Diagram, it is predicted that reaction maybe less efficient due to the large energy difference between the LUMO of diene and HOMO of dienophile. It is suggest that addition of electron donating group on the Diene will lower the energy of LUMO of diene and hence interact more strongly with HOMO of dienophile.

Fig. 4: MO diagram for the formation of the butadiene/ethene TS

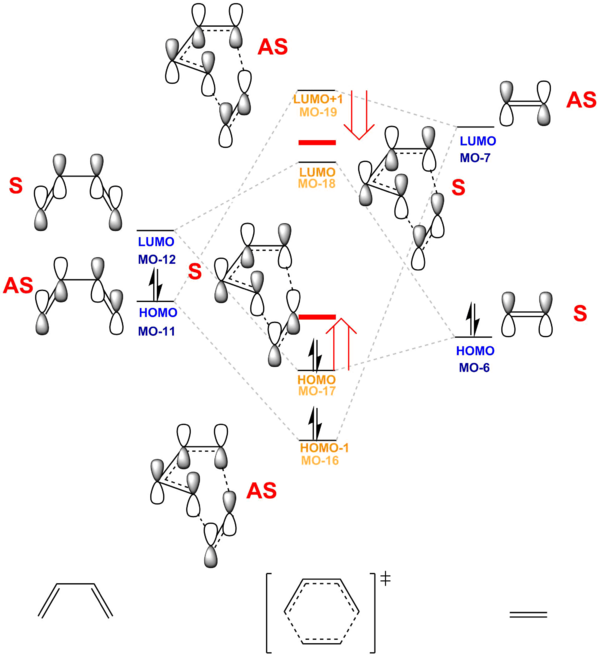
(Fv611 (talk) Your MO combinations are correct, but the energy levels are not. You have correctly calculated the energies of each MO, why not adjust your MO diagram accordingly? For example, you have calculated the energy of the Ethene HOMO to be -0.39, and that of the TS HOMO-1 to be -0.32, yet you draw the TS HOMO-1 lower in energy than the Ethene HOMO.)

Table 2a. HOMO and LUMO of Reactants, Butadiene and ethene

Orbital type	Butadiene	Ethylene
HOMO	MO11, Antisymmetric	MO6, Symmetric
LUMO	MO12, Symmetric	MO7, Antisymmetric

Table 2b. Four MOs produced from reactants for TS

HOMO-1	HOMO	LUMO	LUMO+1
MO 16, Antisymmetric	MO17, Symmetric	MO18, Symmetric	MO19, Antisymmetric

From the MO diagram, it can be concluded that only reactants' MOs of the same symmetry are allowed to react together. Therefore, symmetry of MOs are directly related to the extent of Orbital overlap since reaction cannot proceed with zero orbital overlap. Reaction can only proceed when there is non-zero orbital overlap. Therefore, only interaction between SAME symmetry HOMO and LUMOs (non-zero orbital overlap) are allowed to react. The result is illustrated by the table below.

	Symmetric-Antisymmetric	Symmetric-Symmetric	Antisymmetric-Antisymmetric
Overlap Intergral	Zero	Non-zero	Non-zero
Reaction	Forbidden	Allowed	Allowed

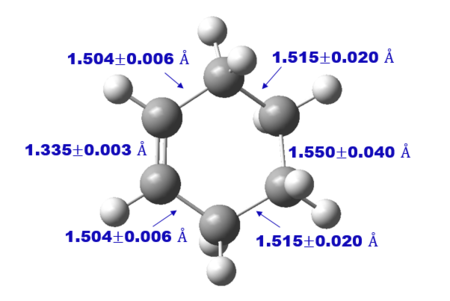
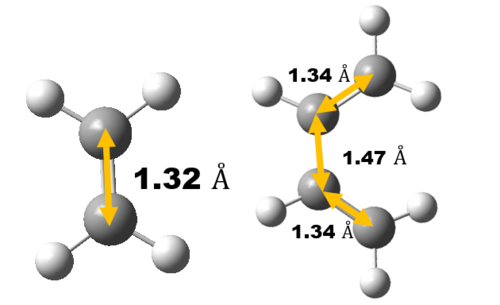
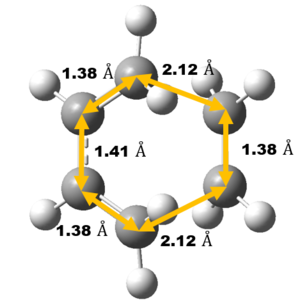
Bond Length Analysis

Table 3. Carbon Carbon bond length of Reactants, TS and Products; and Literature value

Reactant	Transition States	Product	Literature value
			Van der Waals radius of the C atom: 1.7 Å Typical sp3 C-C bond length and sp2 C=C bond lengths  : 1.54 Å, 1.34 Å Bond length of cyclohexene

Experimental carbon carbon bond length of cyclohexene is consistent with the literature value as shown in Table 3 which confirm correct structure of TS and Cyclohexene Product is obtained. Comparing the Van der Waals radius of C atom and the length of the partly formed C-C bonds in the TS, a much lower C-C bond length at TS indicates formation of bond. Typically, sp² C=C bond lengths is much shorter than sp³ C-C bond length as shown in table 3 due to a higher bond order and hence, closer the Carbon atoms are.

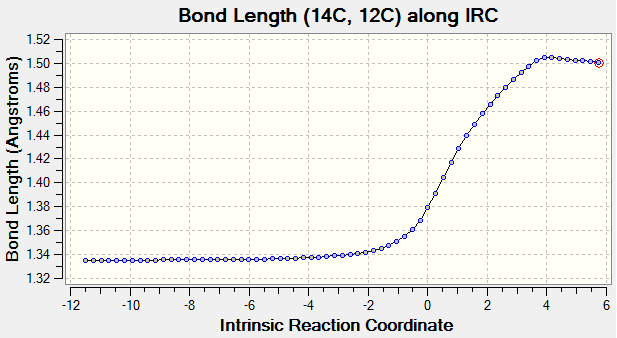
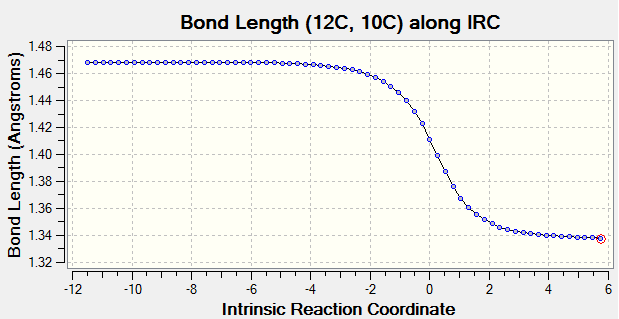
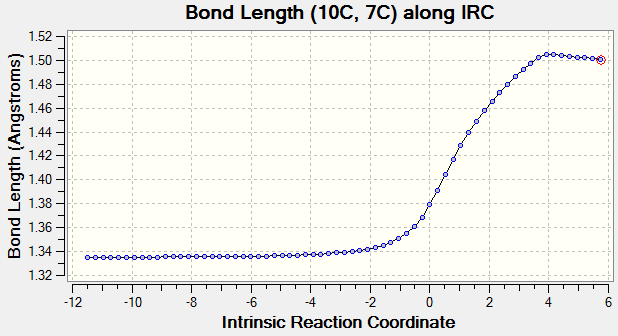
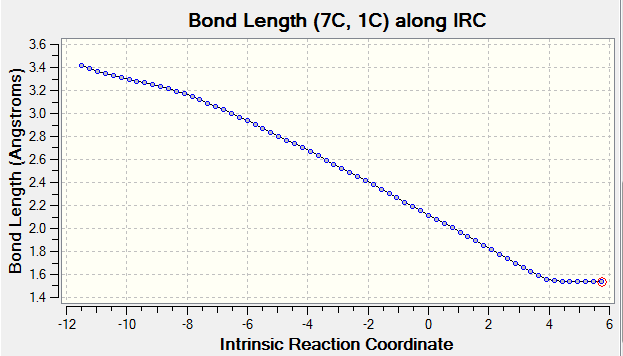
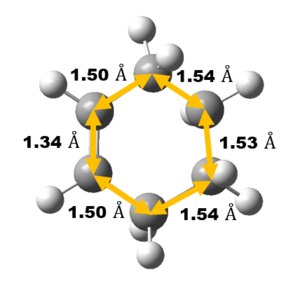
As reaction proceed, bond length corresponds to different carbon atoms change which the result is shown in Table 4.

(Fv611 (talk) There could have been a slightly more wordy discussion, this is more a report on calculated bond lengths than an analysis of what they mean.)

Table 4. Change of Bond Length as the reaction proceed

Fig. 5: Labelled Carbon atoms in reactants

Fig. 6a: Plot of change of Bond Length between C1 and C4	Fig. 6b: Plot of change of Bond Length between C4 and C14	Fig. 6c: Plot of change of Bond Length between C14 and C12
Fig. 6d: Plot of change of Bond Length between C12 and C10	Fig. 6e: Plot of change of Bond Length between C10 and C7	Fig. 6f: Plot of change of Bond Length between C7 and C1

Vibrational Analysis

The vibration that corresponds to the reaction path at transition state is -949.15 cm^-1. In the transition state of this reaction, the two forming bonds have the same lengths. Hence, this confirms the synchronous mechanism where two new bonds are formed simultaneously.

Vibrational Analysis of TS

Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole

Fig. 7: Reaction Scheme of Diels Alder reaction

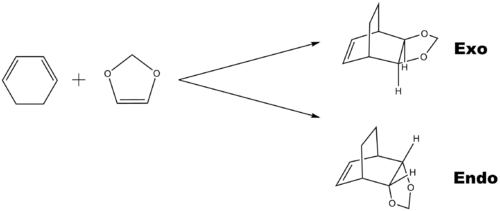
Optimisation Result

Table 5 shows the result of the Optimisation of reactants; endo and exo TSs. It was first optimised at PM6 method then a more accurate method, at B3LYP/6-31G(d) Basis Set

Table 5. Optimization Result of Reactant and Exo, Endo TS at PM6 and B3LYP/6-31G(d) Basis Set

Basic Set	Cyclohexadiene	1,3-Dioxole	Exo TS	Endo TS
PM6
B3LYP/6-31G(d)

Frequency Analysis

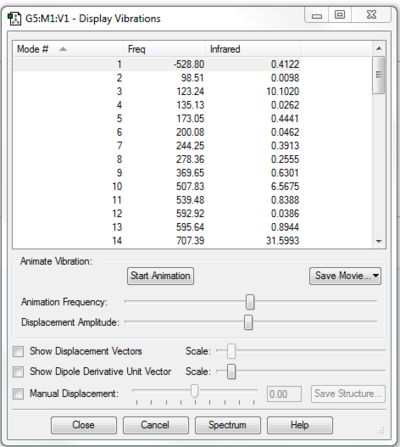
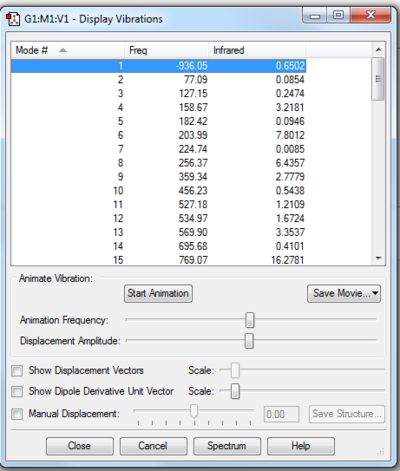
A correct TS is further confirmed by the frequency analysis. Only one negative frequency at Exo and Endo TS indicates a saddle point reached which confirms the correct TS obtained.

Table 6. Frequency Analysis of Exo and Endo TS and Products respectively at PM6 and B3LYP/6-31G(d) Basis Set

	Exo		Endo
	PM6	B3LYP/6-31G(d)	PM6	B3LYP/6-31G(d)
TS	Fig. 8a: Frequency Calculation of Exo TS at PM6	Fig. 8b: Frequency Calculation of Exo TS at B3LYP	Fig. 9a: Frequency Calculation of Endo TS at PM6	Fig. 9b:Frequency Calculation of Endo TS at B3LYP
Product	Fig. 10a: Frequency Calculation of Exo Product at PM6	Fig. 10b: Frequency Calculation of Exo Product at B3LYP	Fig. 11a: Frequency Calculation of Endo Product at PM6	Fig. 11b:Frequency Calculation of Endo Product at B3LYP

---

MO Analysis

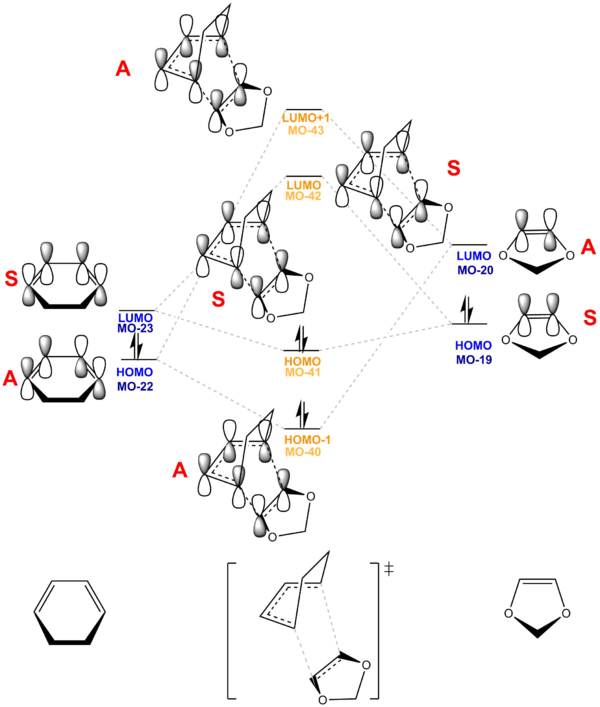
Figure 12 and 13 shows the MO digram for the Diels-Alder reaction (Exo and Endo) , which correlate with the actual MOs performed by Gaussian at B3LYP/6-31G(d) basis set.

Fig. 12: MO diagram for the Exo Diels-Alder reaction

Fig. 13: MO diagram for the Endo Diels-Alder reaction

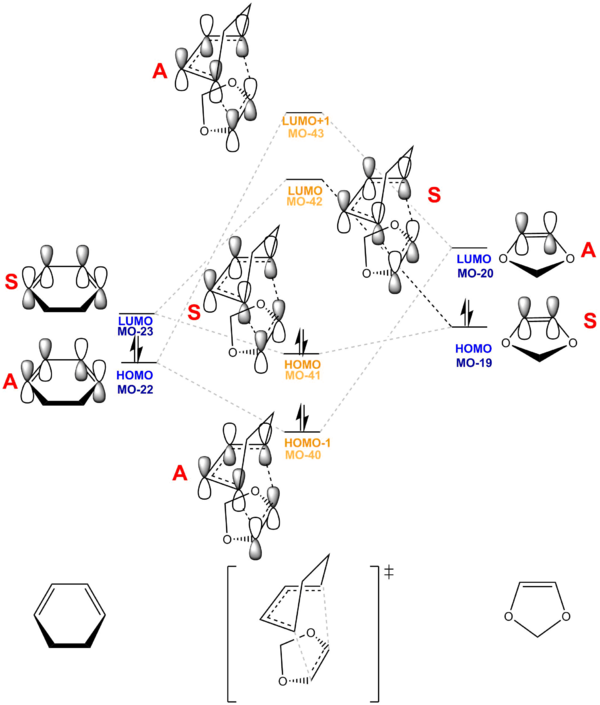(Fv611 (talk) Like in the previous exercise, your pairings are correct but you haven't correlated the positions of your MOs with their computed energies. The dienophile LUMO is the orbital with the highest energy, and the diene HOMO is the orbital with the lowest energy. Additionally, it would have been nice to discuss the difference between Exo and Endo case.)

Table 6. HOMO and LUMO of Exo and Endo TS at B3LYP/6-31G(d)

Orbital type	Exo TS	Endo TS
HOMO-1	MO40, Antisymmetric	MO40, Antisymmetric
HOMO	MO41, Symmetric	MO41, Symmetric
LUMO	MO42, Symmetric	MO42, Symmetric
LUMO+1	MO43, Antisymmetric	MO43, Antisymmetric

This reaction is an inverse demand DA reaction since diene is less electron rich than dienophile in this reaction. The electron-donating oxygen group donate electrons into the double bond dienophile, making it more electron rich.

Hence, the Frontier Molecular Orbitals the LUMO of Cyclohexadiene (Antisymmetric) interact with the HOMO of 1,3-Dioxole, dienophile, are closer in energy than that of HOMO of diene and LUMO of dienophile. As a result, they interact most strongly and form most energetically favourable bond formation. As a result, this reaction is an Inverse Demand DA reaction.

The HOMO-1, HOMO, LUMO, LUMO+1 TS MOs shows A-S-S-A symmetry which further confirm it is an Inverse Demand DA reaction. (Fv611 (talk) This isn't true, as the reaction discussed in exercise 1 also has A-S-S-A symmetry but is a normal electron demand case.)

Reaction Thermodynamics

Table 7. Reaction Energy of Reactants, TS and Product

Basic Set	Cyclohexadiene		1,3-Dioxole		Exo TS		Endo TS		Exo Product		Endo Product
	Energy/ Hatress	Energy/ kJ/mol	Energy/ Hatress	Energy/ kJ/mol	Energy/ Hatress	Energy/ kJ/mol	Energy/ Hatress	Energy/ kJ/mol	Energy/ Hatress	Energy/ kJ/mol	Energy/ Hatress	Energy/ kJ/mol
PM6	0.116878	306.863212	−0.0522760	−137.25064846	0.138903	364.689854	0.137941	362.164123	0.037972	99.6954936	0.037807	99.2622861
B3LYP/6-31G(d)	−233.324375	−612593.19323	–267.068645	–701188.78086	–500.329165	–1313614.3228	–500.332147	–1313622.152	–500.417322	–1313845.779	−500.418691	–1313849.3733

Table 8. Activation Barrier and reaction energy, at room temperature

	Activation Barrier/kJ/mol	Reaction Energy/kJ/mol
Exo Reaction pathway	+168	-63.80491
Endo Reaction pathway	+163	-67.39921

Table 8. shows the result of the Activation Barrier and reaction energy on the reaction of Cyclohexadiene and 1,3-Dioxole. Activation Barrier is calculated by the difference between the energy of product and TS. While Reaction Energy is the differences between product and reactants energies. It is important to note that Basis set of B3LYP/6-31G(d) is used to provide more accurate calculation.

Kinetic favourable of the products can be determined by the Activation Barrier. As shown in Table 8, Endo reaction pathway has a lower Activation energy and hence Endo product is more kinetically favourable. This can be further explained by secondary (non-bonding) orbital interaction in the endo TS HOMO as shown in Table 9. Secondary orbital interaction between diene and the dienophile substituent's π system lowers the energy of the endo TS and hence, lower activation barrier and the reaction proceed much faster towards endo-product. As a result, endo product is more kinetically favourable. On the other hand, there is no such interaction between Diene and the substituents of dienophile in exo TS as shown in the HOMO of exo TS in table 9. Hence, there is no stabilisation of the exo Transistion state. Only primary (bonding) interaction present in the Exo-TS.

Moreover, endo product is more thermodynamically favourable. Comparing the reaction energy between Endo- and Exo- reaction pathway, more negative number is obtained at the reaction towards the formation of Endo-product. Hence, this confirms that the endo-product is more thermodynamically stable. In fact, less sterically-hindered Exo-TS is expected to be more thermodynamically favourable. This unexpected result of Endo-Product being more more thermodynamic favourable of can be explained by Hammonds Postulate. Since this is an endothermic reaction (bond forming), according to Hammonds Postulate, it is expected that TS is more product like. As a consequence, stabilisation by secondary (non-bonding) orbital interaction will also apply to the endo-product.

Table 9. shows secondary orbital interactions or sterics on TS

HOMO of Exo TS	HOMO of Endo TS
Sterics only	Secondary Orbital Interaction

As a result, it can be concluded that inverse electron demand Diels Alder reaction favours endo-Product in terms of thermodynamics and kinetic argument.

Nf710 (talk) 22:02, 29 November 2017 (UTC) Well done your energies look correct and you have come to the correct conclusion. Good understanding of the electon demand of the reaction

Exercise 3: Diels-Alder vs Cheletropic

Fig. 14: Reaction Scheme of the Exo, Endo and Cheletropic pathway

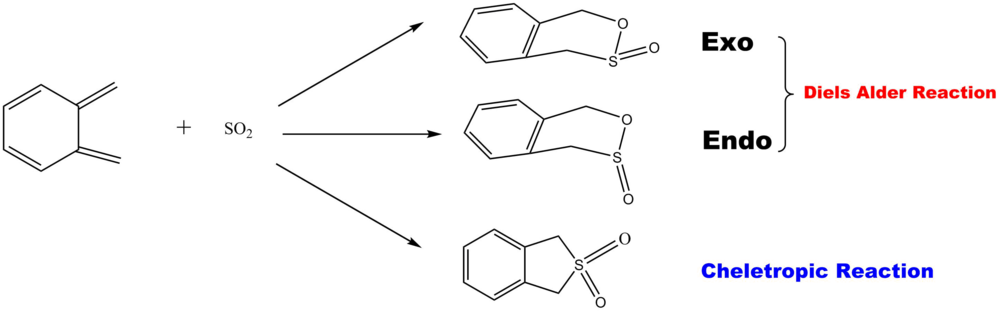
Optimisation Result

Table 10. Optimization Result of Reactants

Xylylene	SO2

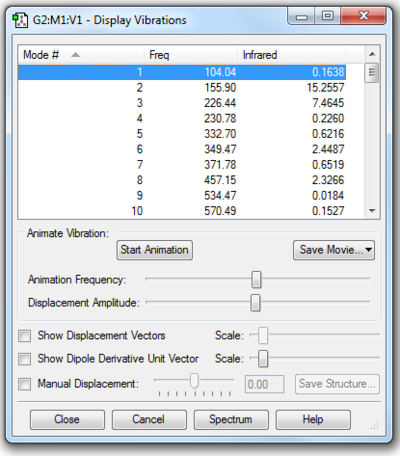
Table 10. shows the optimisation result of reactants. It is confirmed that correct reactants are obtained as there is no imaginary frequency.

Table 11. Optimization Result of Exo, Endo and Cheletropic TS at PM6 Basics Set

Exo TS	Endo TS	Cheletropic TS

Table 11. shows the optimisation result of the exo TS, endo TS and Cheletropic TS at PM6 Basis Set.

IRC Analysis

The reaction coordinate for each path are illustrated in the following animation according to an IRC calculation.

Animation 1. IRC for Endothermic reaction pathway Animation 2. IRC for Exothermic reaction pathway Animation 3. IRC for Cheletropic reaction pathway

Reaction Thermodynamics

Table 12. Reaction Energy of Reactants, TS and Product

Basic Set	Xylylene		SO2		Exo TS		Endo TS		Cheletropic TS		Exo Product		Endo Product		Cheletropic Product
	Energy/ Hatress	Energy/ kJ/mol	Energy/ Hatress	Energy/ kJ/mol	Energy/ Hatress	Energy/ kJ/mol	Energy/ Hatress	Energy/ kJ/mol	Energy/ Hatress	Energy/ kJ/mol	Energy/ Hatress	Energy/ kJ/mol	Energy/ Hatress	Energy/ kJ/mol	Energy/ Hatress	Energy/ kJ/mol
PM6	0.178070	467.522821	−0.118614	−311.421081	0.092078	241.750807	0.090560	237.765298	0.099062	260.087301	0.021455	56.3301068	0.021706	56.9891073	−0.000002	−0.0052510004

Table 12. shows the result of the reaction barrier and reaction energy on the reaction of Cyclohexadiene and 1,3-Dioxole. Activation Barrier is calculated by the difference between the energy of product and TS. While Reaction Energy is the differences between product and reactants energies. It is important to note that Basis set of B3LYP/6-31G(d) is used to provide more accurate calculation.

(B3LYP is a DFT functional, 6-31g(d) is the basis set. You are also not using B3LYP here, so be careful when you copy text from previous sections. Tam10 (talk) 11:24, 24 November 2017 (UTC))

Table 13. Reaction Barrier and energy, at room temperature

	Activation Barrier/kJ/mol	Reaction Energy/kJ/mol
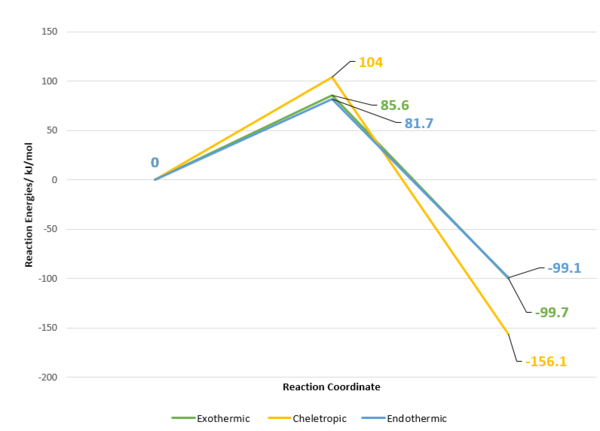
Exo Reaction pathway	+85.6	-99.7
Endo Reaction pathway	+81.7	-99.1
Cheletropic Pathway	+104.0	-156.1

Table 13 shows that the activation and reaction energies for each reaction pathway. It can be concluded that cheletropic pathway is most thermodynamically favorable as the Gibbs free energy of the whole reaction is most negative. However, reaction pathways towards the formation of Cheletropic Product has the highest activation energy. In contrast, Endothermic product is most kinetic favorable. Since it has the lowest activation barrier among other pathway, the rate of reaction towards the formation of endothermic product is the highest. This is demonstrated by figure X the reaction profile for the three pathways.

Fig. 15: Reaction Profile of the Exo, Endo and Cheletropic pathway

(You haven't mentioned the driving force behind these reactions Tam10 (talk) 11:24, 24 November 2017 (UTC))

Extra

The Second cis-butadiene in o-xylylene can undergo another Diels-Alder reaction which illustrated in figure 16.

Fig. 16: Reaction Scheme of the Another Diels Alder reaction between cis-buatadiene and o-xylylene

Table 14. Reaction Energy of Reactants, TS and Product

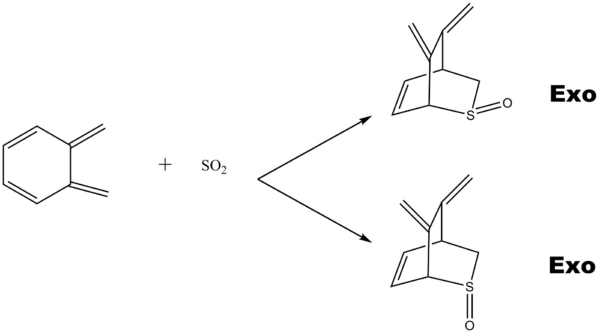
Basic Set	Xylylene		SO2		Exo TS		Endo TS		Exo Product		Endo Product
	Energy/ Hatress	Energy/ kJ/mol	Energy/ Hatress	Energy/ kJ/mol	Energy/ Hatress	Energy/ kJ/mol	Energy/ Hatress	Energy/ kJ/mol	Energy/ Hatress	Energy/ kJ/mol	Energy/ Hatress	Energy/ kJ/mol
PM6	0.178070	467.522821	−0.118614	−311.421081	0.105053	275.816673	0.102071	267.9874309	0.067304	176.7066655	0.065610	172.2590681

Table 15. Reaction Barrier and energy, at room temperature

	Activation Barrier/kJ/mol	Reaction Energy/kJ/mol
Exo Reaction pathway	+119.7	+20.6
Endo Reaction pathway	+111.9	+16.2

Table 14 and 15 show the results of the potential energy of reactants, TS and products; Activation energy and Reaction energy of this Diels-Alder reaction. Activation energy of this Diels Alder reaction is much higher than that of the reaction shown in Ex 3 ( refer to Table 13). Additionally, it is shown that both endothermic and exothermic reaction pathway of this Diels Alder reaction give a positive Gibbs Free energy. As a result, it can be concluded that the endo and exo Diels Alder reaction are very thermodynamically and kinetically unfavourable at this site.

Conclusion

In conclusion, various Diels Alder reaction and Cheletropic reaction pathways are analysed using computational method, Gaussian at PM6 and B3LYP method. At PES, minimum corresponds to reactants and products respectively. There is no imaginary frequency (negative frequency) in both reactants and products. TS corresponds to the first order saddle point which can be further confirmed by vibration calculation in Gaussian. This is confirmed by one negative frequency at TS. Overall, it is shown that computational experimental values are consistent with theoretical prediction.

In the Reaction of Butadiene with Ethylene, it is not very efficient due to the lack of electron donating group present in diene. In the reaction of Cyclohexadiene and 1,3-Dioxole, it is concluded that endothermic product is both kinetically and thermodynamically favourable. This can be explained by the secondary orbital interaction between the diene and substituent of dienophile. In contrast, exo reaction pathway is only favourable by sterics. Frontier Molecular Orbital analysis is also used to confirm the reaction is an inverse electron demand Diels Alder reaction. On the other hand, Diels alder reaction and Cheletropic reaction pathways are compared in the o-Xylylene-SO2 Cycloaddition. Despite the high activation barrier of Cheletropic pathways, it is thermodynamically favourable with the most negative Gibbs Free energy of the reaction. Additionally, a second cis-butadiene fragment in o-xylylene that can undergo a Diels-Alder reaction. However, it is proved that the endo and exo Diels Alder reaction are very thermodynamically and kinetically unstable with positive Gibbs free energy and high activation barrier.

As a result, computation calculation performed by Gaussian provide important insight to thermodynamic and kinetic parameter to Diels Alder reaction and Cheletropic reaction. More advance optimisation and frequency analysis can be completed in the future to provide a more accurate result in the future.

Log Files

Exercise 1

Basics Set	Butadiene	Ethylene	Transition States	IRC	Product
PM6	File:REACTANT1 2 OPTMIN.LOG	File:REACTANT2 OPTMIN.LOG	File:TS 2 OPTTS.LOG	File:TS 2 IRC out.log	File:P FINALOPT 2.LOG

Exercise 2

Basics Set	IRC	Exo-Products	Endo-Products
PM6	File:Endo IRC output final.log File:EXO IRC 5.LOG	File:Yts EXO P FINALOPTMIN 1.LOG	File:Yts ENDO P OPTMIN PM6.LOG
B3LYP/6-31G(d)		File:EXO P FINALOPTMIN B3LYP.LOG	File:Yts ENDO P OPTMIN B3LYP.LOG

Exercise 3

reaction	Xylylene	SO2	IRC	Products
Exo	File:REACTANT 1 OPTMIN 3.LOG]	File:SO2 OPTMIN PM6.LOG	File:3 DA IRC opt.log	File:EX3 EXO P OPTMIN FINAL.LOG
Endo			File:ENDO IRC 6.LOG	File:ENDO P FINAL OPTMIN.LOG
Cheletropic			File:CHEL IRC.LOG	File:CHEL FINALP2.LOG

Extra

Reaction type	Transition States	Products
Exo	File:YTSTSOPTTS EXO.LOG	File:YTS EXO PRODUCT OPTMIN.LOG
Endo	File:YTSTSOPTTS ENDO.LOG	File:YTS ENDO PRODUCT OPTMIN.LOG