Rep:Mod:TSRksg115

Introduction

In this investigation, different reactions were computed using a variety of computational methods on Gaussian and the resulting data was analysed and transition states were inspected.

Quantum Chemistry

Schrodinger's equation,

ĤΨ_a=E_aΨ_a

can help to determine the electronic structure and properties of any molecule. The wave-function contains all information about the molecule and is a function of all the degrees of freedom. With information about electron behaviours in molecules, we can find out all information about their chemistry.

Nf710 (talk) 23:31, 10 January 2018 (UTC) I understand what you are staying, the wavefunction is more a function of electronic position wrt the the nuclei. When the nuclei are fixed. The electronic PES is described by the degrees of freedom as you are measuring how the energy changes as you move the nuclei. so at each point on the PES you calculate a new wavefunction.

To proceed with the wavefunction, we must add more detail to Ψ. We must use a functional form of the set of atomic/molecular orbitals, which is an approximation of the wave function and consists of a linear combination of atomic orbitals (LCAO).¹ A basis set is a set of functions that imitate atomic orbitals, essentially forming the underlying concept of LCAO: they are added together to calculate molecular orbitals. The higher the basis set (the more information it contains), the more accurate the molecular orbital will be, yet this will be more computationally-expensive.

Nf710 (talk) 23:31, 10 January 2018 (UTC) Good understanding of basis sets. In Gaussian they it uses Gaussian functions as our basis functions that model atomic orbitals as they are easier to deal with mathematically. S Slater function is better to model the AOs but they are very complicated to integrate.

Potential Energy Surface (PES)

When we plot the potential energy of a molecule with more than one geometric coordinate, we must use a function using both coordinates. Beyond three dimensions, the graph is called a hypersurface. For a molecule consisting of N_atoms there will be 3N_atoms - 6 independent variables. These variables can include bond lengths, angles etc. This sum specifies the number of internal motions a molecule may possess.

3N_atoms - 6 is derived by:

3N_atoms cartesian coordinates, minus 3 for global rotations and 3 for global translations.¹

The reaction coordinate is a function of all 3N_atoms - 6 internal coordinates.

A stationary point can be defined as having a first derivative equaling 0. The minimum energy point on a PES has a gradient of zero and also a second derivative which would be positive as either left or right of the reaction coordinate will lead to a higher energy. The transition state is a saddle point and will also have a gradient of zero. The transition state will have second derivative which would be negative and it will also produce an imaginary frequency by means of a negative force constant.

Nf710 (talk) 09:08, 11 January 2018 (UTC) You are only talking in terms of the reaction coordinate here. You are correct. But in 3N-6 degrees of fredom, a minimum has a positive second derivative in all dimensions and a TS has positive or all dimensions expect 1 which is the reaction coord, which is positive. You can get this info by finding the eigenvalue of the hessian matrix. (Matrix of second derivatives)

Calculating PES by computational chemistry methods, which solve the Schrodinger equation, allows us to locate and quantify minimum and maximum energy points that represent reactants, products and transition states. These points correlate to different energies that can be used to find energies of reaction or activation energies. This is extremely important in terms of reaction kinetics and it can determine equilibrium and other thermodynamic features of a particular reaction. The Intrinsic Reaction Coordinate (IRC) also gives us the geometries along a reaction coordinate.

Computational Methods

Hartree-Fock Model

By varying the expansion coefficients in the LCAO method to minimize the total molecular potential energy, we can obtain a set of optimal molecular orbitals. These orbitals are one-electron wavefunctions. The Hartree-fock model treats electron motion independent to each other. Electrons typically repel each other due to their negative charges, which is dependent on their relative positions. The model cannot describe this repulsion. Each electron experiences an averaged potential, coming from the electron density of another electron.¹

Nf710 (talk) 09:11, 11 January 2018 (UTC) The mean field comes from all N electrons. So the electron should actually be feeling N-1 electrons potential, but it feels N hence why HF always over estimates the replusion.

Semi-empirical PM6

This method is based on the Hartree-Fock model, but uses empirical data in calculations. It is very useful for working with large molecules whereby the full Hartree-Fock method (no electron interactions) is too computationally-expensive.

By using empirical data, there is some involvement of electron correlation effects, allowing for a more accurate calculation. Semi-empirical methods have their results fitted by parameters, acheiving results best agreeing with experimental data since the Hartree-Fock method can sometimes omit information from calculations.

PM6 methods use parameters to fit experimental data such as dipole moments and geometries.

Density Functional Theory (DFT)

DFT is another computational method. The properties of a many-electron system are found with the use of functionals (functions of another function). For DFT calculations, the functional is the spatially-dependent electron density. Computational costs are lower compared to the Hartree-Fock method and others that use electron correlation.

DFT predicts and calculates on quantum mechanical considerations and does not require parameters or fundamental material properties.

Nf710 (talk) 09:13, 11 January 2018 (UTC) Really good section you have clearly gone away and researched the methods why is good and read beyond the script. Some equations or diagrams would have helped explain some of the concepts possibly.

Exercise 1

The reaction is a pericylic Diels-Alder reaction between cis-butadiene and ethylene to produce cyclohexene. Method 2 (see tutorial) was used for this experiment, with bonds partaking in the reaction being frozen at a distance of 2.2 Å. The experiment was optimised and an IRC was calculated at the semi-empirical PM6 level.

Reaction Scheme

Figure 1. The scheme for the Diels-Alder reaction between cis-butadiene and ethylene.

Molecular Orbital Analysis

Reactants

Figure 2. HOMO and LUMO of the reactants.

	HOMO	LUMO
Ethylene
Butadiene

Transition State

Figure 3. HOMO-1, HOMO, LUMO and LUMO +1 of the product.

	HOMO-1	HOMO	LUMO	LUMO+1
Transition State

MO Diagram

Figure 4. Molecular Orbital Diagram for the Diels-Alder reaction

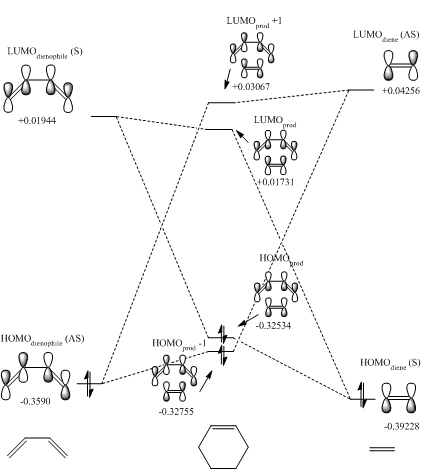
(Fv611 (talk) The MO is good, but there is some confusion on the symmetry requirements and their relationship with the orbital integral. As you have pointed out, only orbitals of the same symmetry are allowed to interact (NB: "symmetrical" and "of the same symmetry" are not equivalent terms). This is because the overlap integral is non-zero for all interactions between orbitals of the same symmetry, while it is equal to zero for two S orbitals or for two AS orbitals. This distinction is not related to the bonding or antibonding character of the interaction. You can find more info here.)

By inspecting Fig. 3, we can see that the HOMO of butadiene is asymmetrical and the LUMO is symmetrical. This is in contrast to ethylene where the HOMO is symmetrical and the LUMO is asymmetrical. Symmetry rules comes from orbital overlap. If there is no orbital overlap, then the interaction is not allowed. When atomic orbitals interact to form molecular orbitals, they must be firstly, close in energy, and secondly, the same symmetry. This is evident in the reaction and shown in Fig. 4 above, where only symmetrical orbitals of reactants combine to form MOs. The HOMO of butadiene and the LUMO of ethylene combine to form HOMO-1, which is a bonding orbital with a non-zero overlap integral. This in turn gives LUMO+1, which is anti-bonding and much higher in energy. The transition state HOMO is a result of a bonding interaction between the LUMO of butadiene and HOMO of ethylene and thus producing the LUMO via an anti-bonding interaction, which has a overlap integral of 0.

Bond Lengths

Figure 5. The changing bond lengths of the reaction.

Butadiene	Ethylene	Transition State	Cyclohexene

According to Fig. 5, the C-C bond lengths change as the reaction proceeds. Initially, the C-C bond in butadiene is 0.147 nm, yet it decreases to 0.141 nm before ending as a C=C bond of length 0.134 nm in the final product. It is evident that in the transition state, the two carbon atoms experience a mid-point between 0.147 and 0.134 nm. For the C=C bonds of butadiene, the lengths are 0.133 nm, compared to ethylene, which is 0.136 nm. In the transition state, the butadiene C=C bonds become 0.138 nm, and finally they become 0.15 nm. Once again, the transition state bond length is an intermediate between the starting reactant and the product. The C=C ethylene bond becomes a C-C bond of 0.157 nm. A typical sp³-sp³ C-C bond length is 0.154 nm, between sp³-sp² 0.150 nm and finally between sp²-sp² carbon centers the length is 0.147 nm. The van der Waal's radius of the Carbon atom is 0.170 nm. The transition state has new bond lengths of 0.211 nm. The sum of two carbon van der Waal radii is 0.340 nm. The new bond length is smaller than that of the van der Waal distance, meaning that there is some interaction occurring and a new bond is forming.

Transition State Vibration

Figure 5. The changing bond lengths of the reaction.

The imaginary frequency of vibration is -948.48 cm^-1. In fig. 5, it is seen that the formation of the two bonds is synchronous, as both butadiene carbons and ethylene carbons approach each other at the same time.

Exercise 2

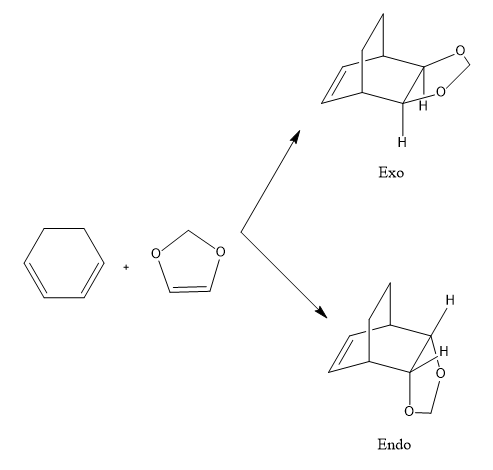
The following exercise consisted of running calculations to find the transition states of both the endo- and exo-product of the pericyclic reaction of Cyclohexadiene and 1,3-Dioxole. For this experiment, Method 2 was used. Firstly, a guess transition state was generated and optimized to a minimum. Secondly, the bonding atoms are frozen and manually set to a distance relating to typical transition lengths. For the carbon-carbon transition state, a length of 2.2 Å was set and then optimized to a transition state. Finally, an IRC calculation took place to show the transition state being a maximum point with a gradient of zero, and also the different geometries on the route between reactants and products. All calculations were initially run using the semi-empirical PM6 method then with the DFT 6-31g(d) method.

Reaction Scheme

Figure 6. The scheme for the Diels-Alder reaction between cyclohexadiene and 1,3-dioxole.

Molecular Orbital Analysis

Reactants

Figure 7. The HOMO and LUMO of the reactants.

	HOMO	LUMO
Cyclohexadiene
1,3-dioxole

Transition States

Figure 8. The HOMO-1, HOMO, LUMO and LUMO+1 of each product.

	HOMO -1	HOMO	LUMO	LUMO +1
Endo Product
Exo Product

Molecular Orbital Diagrams

Figure 9. Molecular Orbital Diagram for the exo transition state.

Figure 10. Molecular Orbital Diagram for the endo transition state.

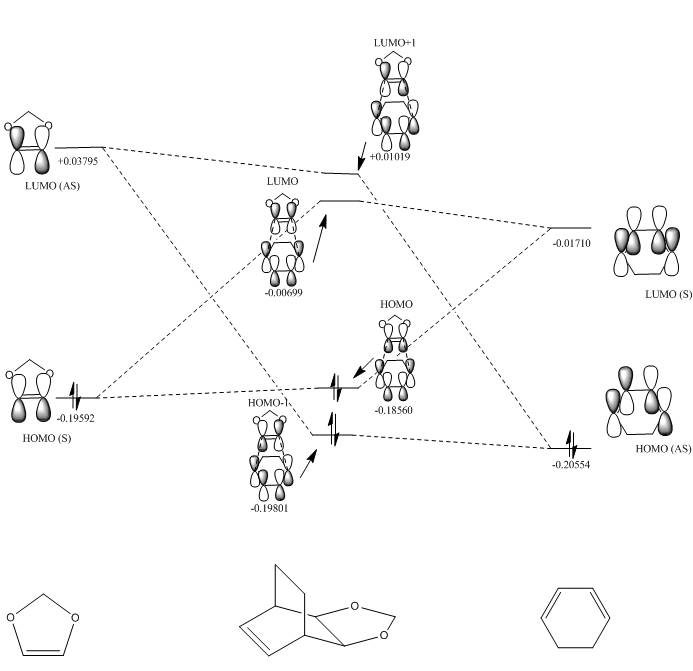
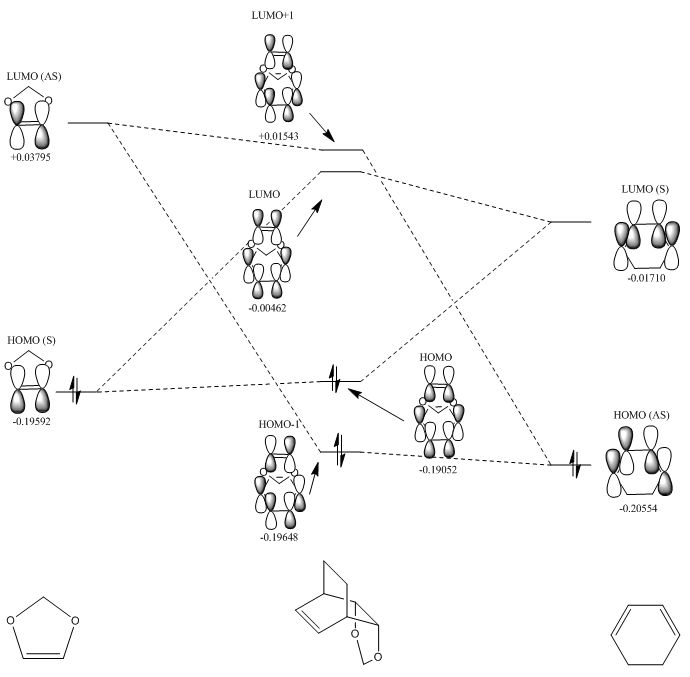
As you can see from Fig. 9 and Fig. 10, the molecular orbital pairing of the reactants are different from the Diels-Alder reaction seen in Exercise 1. In Exercise 1, the HOMO of the dienophile interacted with the LUMO of the diene, however in this experiment, the reactant molecular orbital energies are different. There is an electron rich-dienophile as the oxygens in 1,3-dioxole are electron-donating, raising energy levels. The transition state molecular orbitals follow the same rules of symmetry as in Exercise 1, whereby only orbitals of similar energy and symmetry interact to give a non-zero overlap integral. This can be seen in Fig. 8, where HOMO-1 and HOMO have a bonding interaction, and LUMO and LUMO-1 have an anti-boding interaction (zero overlap integral). The HOMO of the diene thus interacts with the LUMO of the dienophile, which is representative of an inverse electron demand system.

(Fv611 (talk) The MO diagrams are very nice, but it would have been nice to add a critical assessment on why the relative energies of the TS MOs are different across the exo and endo cases. Additionally, it is important to note that the same orbitals as in Exercise 1 are combined in this reaction to form the TS MOs. The inverse electron demand character is not given by the interacting pairs (diene HOMO and dienophile LUMO combine both in this and the previous reaction), but by the relative energies of the MOs. This is an inverse electron demand because the lowest energy HOMO is the dienophile's instead of the diene's.)

Reaction Calculations

The data in Table 1 (below) was used to analyse the different reaction pathways of the endo and exo product. The reactants were individually optimized using the DFT-B3LYP method and their energies were added together.

Table 1. The energies of various reaction properties.

	Reactants (kJ/mol)	Transition State (kJ/mol)	Product (kJ/mol)	Activation Barrier (kJ/mol)	Reaction Energy (kJ/mol)
Endo	-1313781.97	-1313622.16	-1313849.37	159.81	-67.40
Exo	-1313781.97	-1313614.32	-1313845.78	167.65	-63.81

Figure 11. A reaction profile of both the endo and exo pathway.

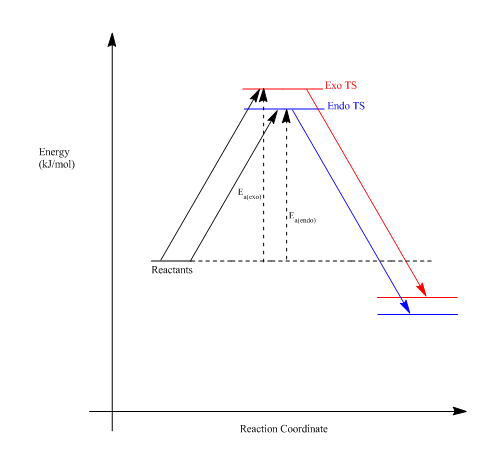
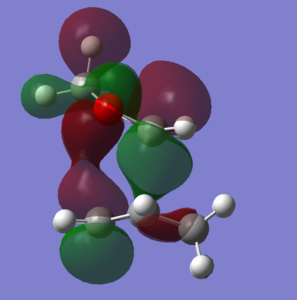
According to the data, it can be seen that the exo product has the greatest activation barrier, with a difference to the endo product of around +7.84 kj/mol. The exo product also has a greater reaction energy. The endo pathway is likely to produce the kinetic product, as the activation energy is lower. It is possible that this can be a result of the stabilized transition state structure by means of secondary orbital interactions between the oxygen and diene p-orbitals (Fig. 12). This secondary orbital interaction does not occur with the exo transition state as, geometrically, the oxygen p-orbitals are not close enough to have this stabilization.

Figure 12. Secondary orbital interaction of the Endo-TS.

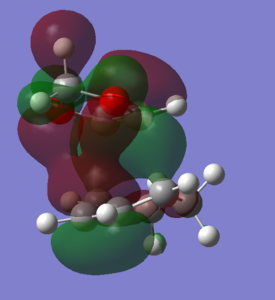
Generally, the exo product is the thermodynamic product in Diels-Alder reactions, however, it is higher in energy than the endo-product. In Fig. 13, it can be seen that there could be possible steric clashes between the hydrogens of the 1,3-dioxole group and the hydrogens from the cyclohexadiene ring. This can raise the energy of the product, which is also quantitatively shown in Fig. 13. The endo-product is therefore the expected major product, as it is both the kinetic and thermodynamic product.

Figure 13. Steric clash in the exo-product.

Supporting Files

Endo product: File:Ksg115 ENDO PRODUCT EX 2 B3LYP OPT.LOG Exo product: File:Ksg115 EXO PRODUCT OPT B3LYP.LOG

Nf710 (talk) 09:18, 11 January 2018 (UTC) Good section. Nice use of diagrams. Your energies are correct and you have come to the correct conclusions. You could have quantitatively investigated the orbital energies by runnign a single point energy calculation with both reactants on the same potential energy surface and then looking at the MOs

Exercise 3

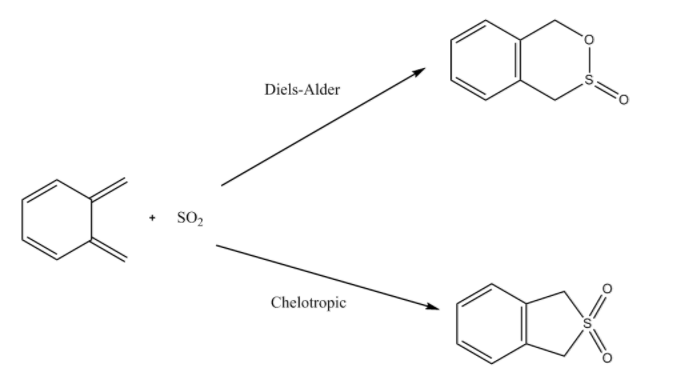
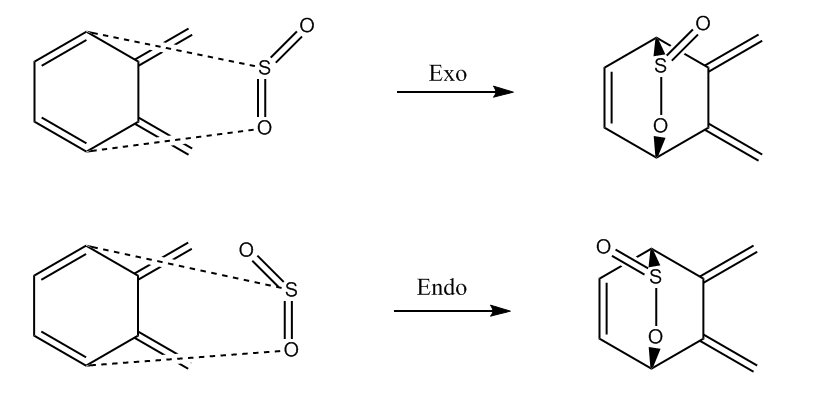
The following exercise involved the hetero-Diels-Alder reaction of SO₂ with o-Xylylene. The diene in this case is SO₂. Method 3 was used in this experiment. The guess product was made firstly and then optimized to a minimum using the semi-empirical PM6 method. The bonds corresponding to the new product were then altered: C-S 2.4 Å and C-O 2.0 Å. They were then frozen and optimized and an IRC calculation was then applied. As well as the Diels-Alder reaction, there is a possible cheletropic reaction possible. The transition state and IRC was calculated for all reaction types.

Reaction Scheme

Figure 14. The scheme for the reaction between Sulfur Dioxide and o-Xylylene.

IRC Calculations

Figure 15. The IRC videos of each possible reaction pathway.

Reaction Type	IRC	Energy along the IRC
Endo-Diels-Alder
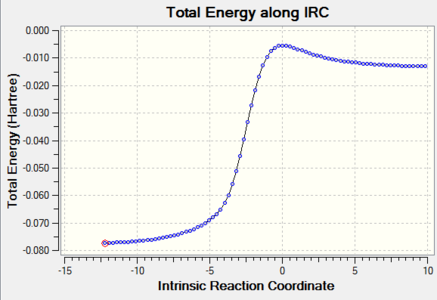
Exo-Diels-Alder
Cheletropic

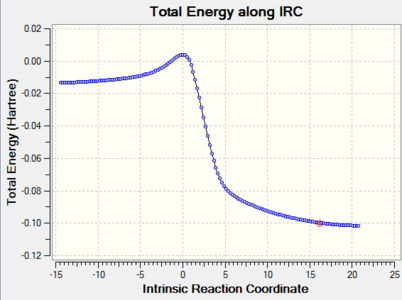
Reaction Calculations

Table 2. The energies of various reaction properties of Sulfur dioxide and o-Xylylene.

	Reactants (kJ/mol)	Transition State (kJ/mol)	Product (kJ/mol)	Activation Barrier (kJ/mol)	Reaction Energy (kJ/mol)
Endo	156.62	237.77	56.99	81.14	-99.63
Exo	156.62	241.75	56.33	85.13	-100.29
Cheletropic	156.62	260.08	-0.01	103.46	-156.63

(Useful to put the values of the barrier and reaction energies into the diagram below. Makes comparison easier Tam10 (talk) 16:14, 4 January 2018 (UTC))

Figure 16. The energies of the different pathways available for the reaction involving the terminal cis-butadiene.

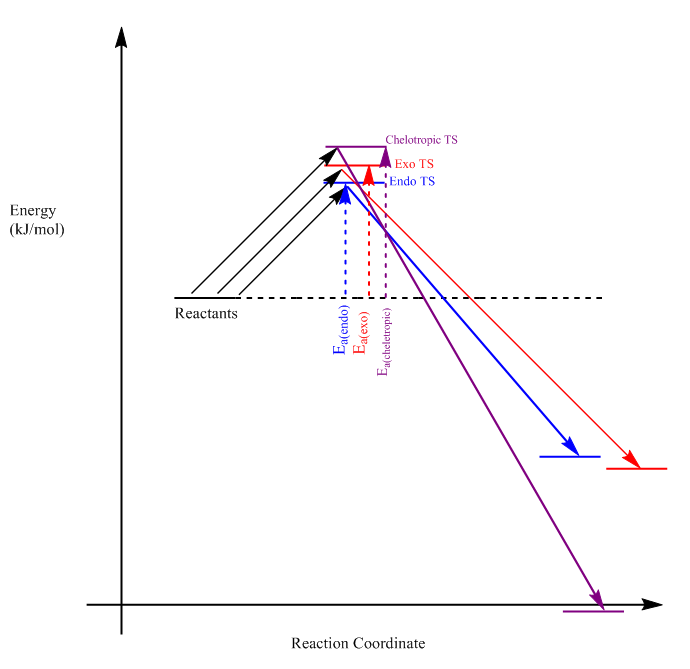
As you can see from Fig. 16, the endo-TS has the lowest energy and the endo-product has the highest energy, thus the endo-route will produce the kinetic-product. Once again, the endo-TS may be stabilized by the secondary orbital interactions of the sulfur dioxide oxygen p-orbital and the diene orbitals. The highest activation energy comes from the cheletropic-TS, which is 8.33 kj/mol greater than the exo-TS, yet the cheletropic product is the most energetically-stable (thermodynamic product). A reason for this could be; firstly, the formation of a 6-membered aromatic ring which is energetically-stable, and secondly, the conservation of two strong S=O bonds in the product, compared to only one S=O in either Diels-Alder products.

(cheletropic TS is 18 kJ/mol higher than exo TS. All products have the 6-membered aromatic ring. However, S is a lot larger than C and places strain on the non-aromatic ring, so the 5-membered ring could be more sterically stable Tam10 (talk) 16:14, 4 January 2018 (UTC))

Side Reactions

There is a second cis-butadiene fragment that the diene may react with in a Diels-Alder fashion, Fig. 17. This possible side-reaction was examined by IRC, Fig. 18, and optimized using the semi-empirical PM6 method.

Figure 17. The scheme for the reaction with the internal cis-butadiene fragment.

Figure 18. The IRC videos of the reaction pathway using the internal cis-butadiene.

Reaction Type	IRC	Energy along the IRC
Endo-Diels-Alder
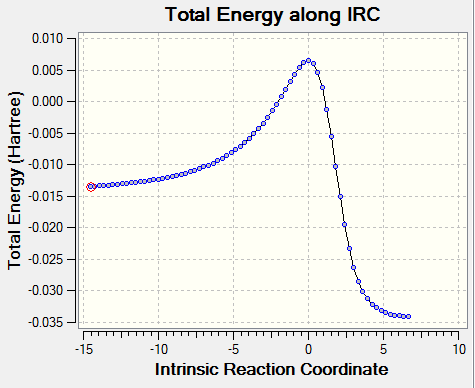
Exo-Diels-Alder

Table 3. The energies of various reaction properties of Sulfur dioxide and o-Xylylene with the internal cis-butadiene fragment.

	Reactants (kJ/mol)	Transition State (kJ/mol)	Product (kJ/mol)	Activation Barrier (kJ/mol)	Reaction Energy (kJ/mol)
Endo	156.62	267.99	172.26	111.37	+15.64
Exo	156.62	275.82	176.71	119.20	+20.09

As you can see from Table 3, the activation barriers for the internal Diels-Alder reactions are much higher than the terminal cis-butadiene. For the endo-product, the difference is +30.22 kJ/mol and for the exo-product, the difference is +36.12 kJ/mol. This could be due there being more steric-hindrance to reach the internal cis-butadiene. The resultant products are also greater in energy to the terminal reaction; endo +115.27 kJ/mol and exo +120.38 kJ/mol. This could be a result of steric-clashes by the S=O fragment and the terminal cis-butadiene (exo-product) or with the alkene fragment seen in the endo-product.

(I would guess that there are two reasons the TS is higher in energy. First, the exocyclic reactions gain some aromaticity in the TS, lowering the TS and products. Secondly, the two carbon atoms in the endocyclic reactions have to sp3 hybridise, causing a huge distortion of the system - a lot of the bonding interactions become much less efficient in the transition Tam10 (talk) 16:14, 4 January 2018 (UTC))

Supporting Files

Reactants: Sulfur Dioxide File:Ksg115 SO2.LOG, o-Xylylene File:Ksg115 o-XYLYLENE PM6 OPT.LOG.

Exo-product (terminal): Transition State File:Ksg115 XYLYLENE-SO2 terminal exo TS BERNY PM6.LOG, Product File:Ksg115 XYLENE-SO2 exo OPT PM6 PRODUCT.LOG.

Endo-product (terminal): Transition State File:Ksg115 XYLYLENE-SO2 endo terminal PM6 TS BERNY.LOG, Product File:Ksg115 XYLENE-SO2 ENDO PRODUCT PM62.LOG.

Cheletropic: Transition State File:Ksg115 CHELO OPT PM6 TS BERNY.LOG, Product File:Ksg115 CHELO PRODUCT OPT PM6.LOG.

Exo-product (internal): Transition State File:Ksg115 terminal exo PM6 TS berny.LOG, Product File:KSG115 EXO EXTRA EX3 OPT PM6.LOG.

Endo-product (internal): Transition State File:Ksg115 internal endo Ts pm6.LOG, Product File:KSG115 EXTRA ENDO EX3 PM6.LOG.

Further Work

As an extension, another electrocyclic reaction was optimized. 1,3-cyclooctadiene is an 8-membered ring structure with two double bonds that can undergo a ring-closure through the use of PhLi. The resulting product is a bicyclic structure with two 5-membered rings fused and only one of the alkene bonds preserved, Fig. 19.

Reaction Scheme

Figure 19. The scheme showing the electrocylic ring-closure reaction of 1,3-cyclooctadiene.

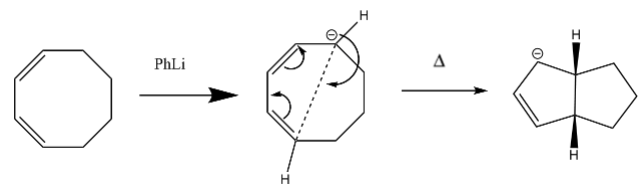
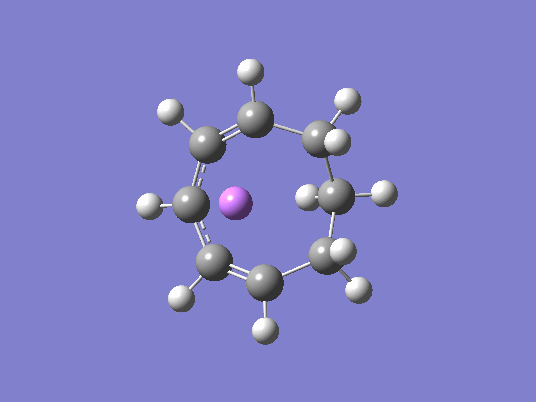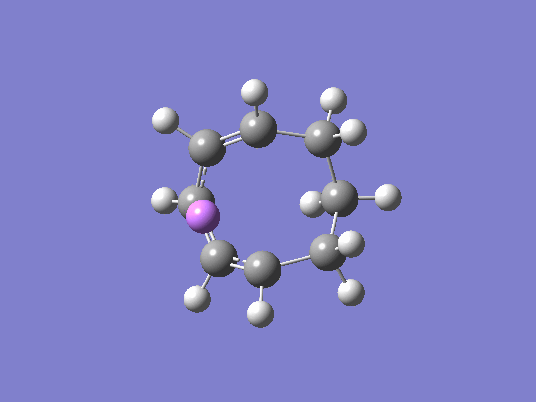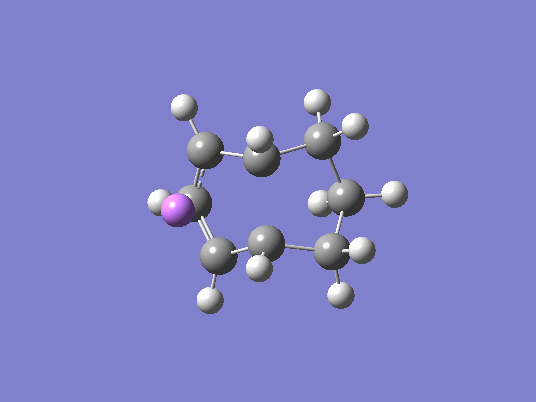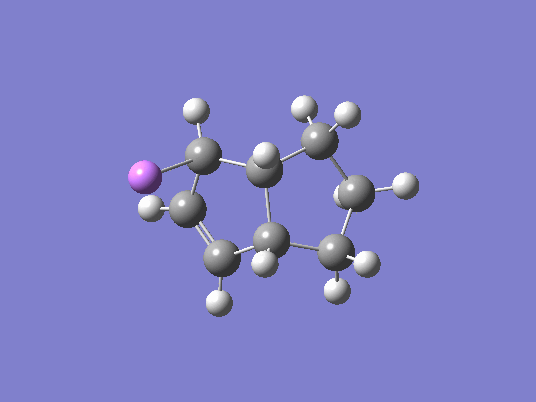
Method 2 was used to optimize the reaction. The PhLi removed a hydrogen from the ring and the negative charge was stabilized by a lithium ion. The carbons involved in the ring closure were both frozen at a distance of 2.2 Å and then optimized. An IRC was also calculated for the reaction, Fig. 20. The purpose of the experiment was to attempt to visualize the electrocyclic reaction in terms of charges, and how the lithium moves around the ring, essentially following the negativity.

(This is an interesting section that could lead to a mini-project. There is more investigation into the energetics needed - Lithium is a hard cation and "prefers" localised charges. This could be another explanation for the exothermic product. I would suggest trying different counterions to see if the energetics are changed. Then you would be able to make a stronger conclusion Tam10 (talk) 16:29, 4 January 2018 (UTC))

(+8% Tam10 (talk) 16:29, 4 January 2018 (UTC))

IRC Animation and Charge Distributions

Figure 20. A video showing the change from reactants to products.

Figure 21. An assortment of different stages of the calculated IRC showing their charge distributions.

IRC Structure	Charge Distribution
Reactant
Frame 31
Frame 53
Transition State
Frame 103
Product

As you can see from Fig. 21, the charge distribution changes across the molecule. With the proceeding reaction, Fig. 20, the lithium ion follows the developing negative charge around the ring structure all the way to the products, where it acts as a counter-ion to the localized negative charge on one of the carbons.

Reaction Calculations

Table 4. The energies of different reaction properties for the electrocylic ring-closure.

Reactants (kJ/mol)	Transition State (kJ/mol)	Product (kJ/mol)	Activation Barrier (kJ/mol)	Reaction Energy (kJ/mol)
432.58	614.49	414.90	181.91	-17.68

The second part of the reaction, the electrocyclic rearrangement, was an exothermic process. The bi-cyclic product was more stable and lower in energy than the octadiene ring. This could be due to the fact that 5-membered rings have interior angles that are 108 ^o. This is complimentary to sp³ orbitals, which ideally would like angles of 109.5^o. This is much in contrast to the the octagonal starting reactant, which has angles of 135 ^o.

Transition State Vibration

Figure 22. The ring-closure transition state vibration.

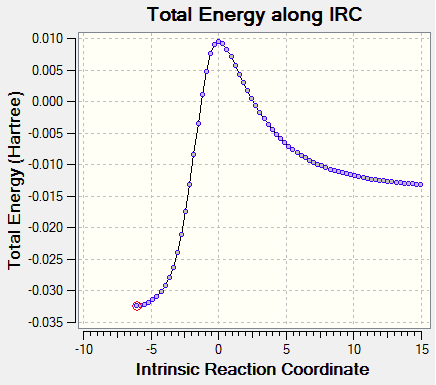
The imaginary frequency of vibration is -600.50 cm^-1 as shown in Fig. 22.

Supporting Files

Reactants File:Ksg115 OCT-LI REACTANTS PM6 OPT.LOG, Transition State File:Ksg115 OCT-LI TSTATE PM6 OPT.LOG, Product File:Ksg115 OCT-LI PROD PM6 OPT.LOG.

Conclusion

In Experiment 1, it was seen that only orbitals of the same symmetry could interact and in turn, give a non-zero overlap integral. This is in contrast to orbitals of opposite symmetry which give an anti-bonding interaction and an overlap integral of zero. We also saw that the transition state bond lengths were intermediates of an sp² and sp³ bond length when they were changing type. Building on the symmetry rules of exercise 1, we could see the same patterns being followed in exercise 2. However in this case, the Diels-Alder reaction proceeded with inverse-electron demand in terms of orbital interaction. The presence of electron-donating oxygen atoms raised the energy levels of the dienophile and the HOMO then interacts with the LUMO of the diene, which is the reverse of the interactions in Exercise 1. In Exercise 2, we also saw how the endo-TS is lower in energy by means of a secondary orbital interaction. Exercise 3 followed 5 different reaction pathways to find which processes would be energetically-favored. It was found that the kinetic product would be the endo-Diels-Alder reaction using the terminal cis-butadiene fragments and the thermodynamic product being the cheletropic. The extension was carried out to show that there is a favorable ring-closure of an cyclooctadiene species, and the reaction was simulated to show how charge distribution changes as the reaction proceeds.

References

1. Theoretical and Computational Chemistry Series Computational Quantum Chemistry 2013, 1–62.