Rep:Mod:TSKFL

Introduction and Methodologies

The simulation investigates the energies of the transition states of Cope Rearrangement and Diels-Alder reactions so that specific reaction paths may be derived. Cope rearrangement is a [3,3]-sigmatropic re-isomerization of 1,5-hexadiene, which can proceed via a 'chair' or a 'boat' transition state. On the other hand, the 4n+2 π Diels-Alder reaction observed is between maleic anhydride (dienophile) and cis-butadiene and is dependent on the symmetries of the participating orbitals to ensure sufficient overlap densities. Transition states, by definition, cannot be isolated separately, and therefore to calculate activation energies of different reactions, computational methods are required. To derive the transition state, three methods are used and compared: Hartree-Fock, DFT and semi-empirical approaches.

Hartree-Fock Method, Density Functional Theory and Semi-Empirical Methods

In observing the Cope Rearrangement, the Hartree-Fock method is employed to optimize the reactants and the transition structure. The Hartree-Fock method seeks to solve the electronic Schrodinger equation that is described by single-particle wavefunctions, where each electron is independent of other electrons. More specifically, the HF method does not take into account Coulombic interactions as it uses a single-determinant approximation (this is referred to as Slater determinants, which are solutions to antisymmetrical wavefunctions with more than two electrons). For each calculation, the basis set will be defined, which refers to the set of one-electron wavefunctions to be linearly combined to create MOs. 3-21G is the minimal basis set used in this exercise, which is a simple basis set giving reasonable energies approximations for hydrogen and carbon atoms. An improvement to the Hartree-Fock method involves improving the basis set to 6-31G, which adds polarization to the non-hydrogen atoms, and therefore refines the energy calculations.

The DFT (density function theory) is another method of calculation that investigates many-body systems based on the electron density instead of wavefunctions (which are the mathematical constructs that form the basis of the Hartree-Fock calculations). Unlike the HF method, the DFT calculations consider electron correlations such that all electrons experience the external potential and Coulombic interactions with other electrons.Both methods treats exchange energy exactly; and that the exchange energy is pronounced in the process of minimizing the transition state structures given that it contributes to chemical bonding.

Finally, the semi-empirical method is used specifically for modelling the Diels-Alder reactions, which provides an improvement to the assumption-based Hartree-Fock method by replacing a number of calculations with empirical results. This is particularly applicable for large systems (such as Diels-Alder transition states) given the number of atoms involved, and therefore computational resources can be conserved using experimental information regarding bond distances and other atomic properties.

Nf710 (talk) 12:36, 21 January 2016 (UTC) Very good understanding of the methods and how a slater determinants is essentially an antisymetrised hartree product. semi empirical methods are typically parametrised for the atoms present on test molecules.

Reaching the transition states

In tandem with either one of the computational method, there are also several options in reaching the transition state on the PES surface. This simulation will consider transition state optimization performed using TS(Berny), frozen coordinates method and QST2. All methods seek to provide geometry optimization as to derive electronic energies and transition states representative of the reactions. TS(Berny) involves optimizing a 'guessed' transition structure to the "saddle-point" of the transition structure, and is therefore most applicable for simple systems where the correct trajectory can be approximated with reasonable accuracy. Secondly, the frozen coordinate methods involve freezing the coordinates of atoms that are involved in the bond forming/breaking processes while optimizing the rest of the structure before finding the changes in the bond forming/breaking sites. Finally, the QST2 method finds the energy maxima (the transition state) by interpolating the reactant and the product structures.

Optimization of selected 1,5-Hexadiene Conformers

This section involves the energetic analysis of various conformers of 1,5-hexadiene, which are expected to vary according to the dihedral angles across the carbon framework.

Structure	Level of Calculations	Energetic Values (a.u.)	Symmetry	Log file source
1,5-hexadiene - anti4	HF/3-21G	-231.69097055	C1	File:ANTI COPE OPT 2.LOG
1,5-hexadiene - gauche	HF/3-21G	-231.68776100	C2	File:GAUCHE COPE OPT.LOG
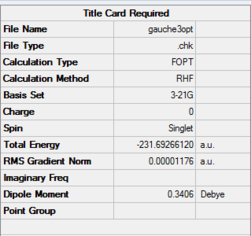
1,5-hexadiene - gauche3	HF/3-21G	-231.69266120	C1	File:GAUCHE3OPT.LOG
1,5-hexadiene - anti2	HF/3-21G	-231.69253516	Ci	File:CI INPUT HF.LOG
1,5-hexadiene - anti2	DFT/6-31G	-234.61171162	Ci	File:CI INPUT DFTV2.LOG

Table 1: All derived results from optimizing the low-energy conformers of 1,5-hexadiene.

Anti4 Conformer	Anti2 Conformer	Gauche Conformer	Gauche3 Conformer

Table 2: Newman projections of all calculated 1,5-hexadiene conformers showing how energetic differences arise due to steric clashes

Optimizing the Anti4 and Gauche conformers at HF/3-21G level

1,5-hexadiene are built on Gaussview and then rotated correspondingly to derive specific conformers. For the anti-conformation, this involves 180^o dihedral angle between the alkenyl groups, and for the gauche-conformation, this involves a 60^o dihedral angle. To ensure that the starting geometry is correct, the 'Symmetrize' function is used so that the point groups are derived. The HF method used is based on the determinant of many single-electron wavefunctions in the molecule, which is the Slater determinant; and operating on the 3-21G level involves general approximations for the C and H atoms.

1,5-hexadiene with anti-periplanar conformation is optimized using Hartree-Fock method with 3-21G basis set. The total energy calculated is E = -231.69097055 a.u. and possesses a C₁ symmetry point group. Additionally, gauche 1,5-hexadiene was optimized resulting in total energy, E = -231.6877610 a.u. with a C₂ symmetry point group. The energetic difference results from increased steric clashes in gauche conformation. The key expectations are that the anti-periplanar conformers would result in structures that are more stable, primarily due to the arrangement of the bulkiest groups. Given that the optimizations of these conformers are achieved using the Hartree-Fock method, it is important to note that the HF method uses single-determinant approximation instead of a more rigorous antisymmetrical wavefunctions in the case of multi-electron system (as for 1,5-hexadiene). As a result, the coulombic interactions are ignored in these optimizations.

Structure	Level of Calculations	Results Summary	Point Group	Total Energy (a.u.)
Anti4 1,5-hexadiene	HF/3-21G		C1 Point Group	-231.69097055
Gauche 1,5-hexadiene	HF/3-21G		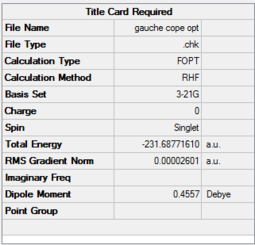C2 Point Group	-231.68776100

Table 3: Summary of anti 1,5-hexadiene and gauche 1,5-hexadiene conformers

Lowest Energy Conformers

The predicted lowest energy conformation is a structure corresponding to anti2 conformers, shown below:

Newman-like projection of anti-periplanar anti2 conformer showing 180 degrees dihedral angle between the bulkiest groups.

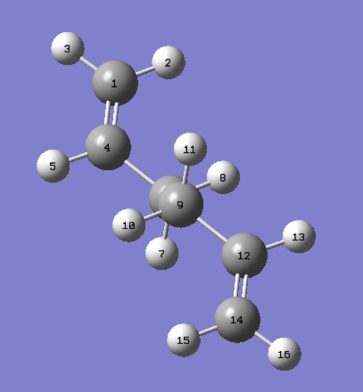
This is due to the fact that only in this anti-periplanar arrangement, the two bulkiest alkenyl groups have 180 degrees torsional angle along the C2-C3-C4-C5 bond. As a result, steric strain in the anti-periplanar conformer would be expected to reduce. Contrary however, the gauche3 conformation undergoing the HF/3-21G level of calculations resulted in lower energy. The results of both calculations are shown below:

Structure	Level of Calculations	Results Summary	Point Group	Total Energy (a.u.)
Anti2 1,5-hexadiene (Predicted lowest energy conformer)	HF/3-21G		C2 Point Group	-231.69253528
Gauche3 1,5-hexadiene	HF/3-21G		C1 Point Group	-231.69266120

Table 4: Summary of results comparing the actual most stable 1,5-hexadiene conformers.

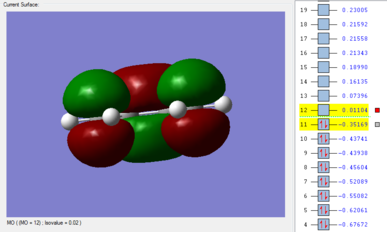
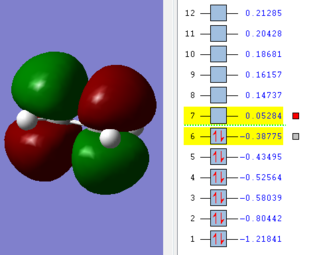
The energetic difference between the two conformers on Table 4 is slight, 0.000123 a.u. or ~0.0790 kcal/mol. Visualizing the HOMO of the gauche3 conformer reveals that there is a certain degree of orbital overlap between the π systems within the hexadiene structure, leading to increased stabilization. This is not observed for anti-periplanar conformation, as the alkenyl fragments are on opposite faces.

π Orbital overlap within the gauche3 conformer made possible by the twist in the conformer (right hand side).

Comparing DFT Theory with Hartree-Fock Method

The C_i conformer is built on Gaussview and then optimized first using the HF/3-21G level of theory and then DFT B3LYP/6-31G(d) level of theory is performed on the structure. Given that each method uses different approximations to calculate the total energy, the accuracy of either theory should be reflected on the geometries of the final structures instead, as shown below:

Ci optimized 1,5-hexadiene with labelled atoms

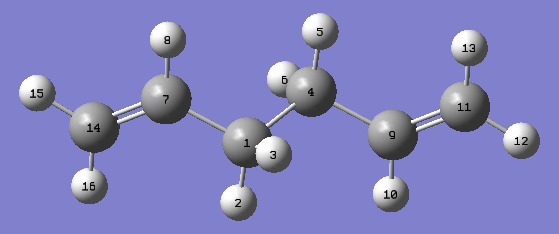
Bond Lengths (Å)	HF/3-21G	B3LYP/6-31G (d)	Literature Values
C1 - C4	1.55317	1.54839	1.538 + 0.027
C1 - C7	1.50882	1.50422	1.508 ± 0.012
C7 - C14	1.31618	1.33825	1.340 ± 0.003

Table 5: Comparison of bond lengths generated from DFT and HF optimizations.

Dihedral Angle	HF/3-21G	DFT/6-31G (d)
C4-C1-C7-C14	114.626	118.580
C9-C4-C1-C7	180.000	180.000

Table 6: Comparison of dihedral angles generated from DFT and HF optimizations

The C=C bond length (C₇ - C₁₄) and the C-C bond length (C₁-C₄) calculated for the Hartree-Fock method are both shorter than the DFT/6-31G(d) optimization. Comparison with the literature values indicate that calculations at the B3LYP/6-31G(d) level resulted in a double bond length that corresponds more closely with actual C=C bond lengths. However, the opposite is observed for the C-C bond lengths, where the HF/3-21G level of calculations resulted in closer bond lengths to experimental results.The increased accuracy in the bond lengths using the 6-31G basis set could be accounted by the inclusion of polarization to all atoms and therefore models the core electrons more accurately; and could possibly suggest that calculations using electron densities instead of orbital overlaps is more accurate for non-sp³ hybridized atoms. Overall, the geometry changes are minimal, with the largest bond lengths difference equal to ~0.02x10^-10 magnitude. The degree of polarization becomes important as the structure becomes larger and more complex (with more heteroatoms), which is not as applicable in the case of 1,5-hexadiene. As a result, both methods are adequate for optimization.The central carbons' dihedral angle was initially set to 180^o, which has remained unchanged through either one of the calculations, suggesting that both methods are equally accurate in this particular aspect of geometry optimization.

Nf710 (talk) 14:25, 21 January 2016 (UTC) Excellent deduction and use of literature for comparison

Thermochemistry Analysis

Additional frequency calculations enable more specific energetic values to be calculated, with the inclusion of other parameters. The DFT B3LYP/6-31G(d) optimized structure is then subjected to a frequency calculation at the same level of theory. All resultant vibration modes are positive and therefore suggest that the structure is at the minimum of the PES surface. The infrared spectrum and thermochemistry analysis of the molecule are shown below:

IR Spectrum of the B3LYP/6-31(d) optimized anti2 conformer of 1,5-hexadiene

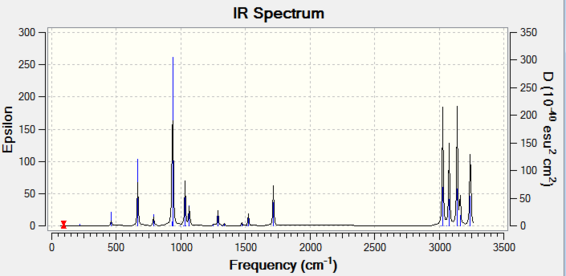
Structure	Level of Calculations	Temp (K)	Sum of electronic and zero-point energies (a.u.)	Sum of electronic and thermal energies (a.u.)	Sum of electronic and thermal enthalpies (a.u.)	Sum of electronic and thermal free energies (a.u.)
Ci 1,5-hexadiene	DFT B3LYP/6-31G(d)	100.00	-234.469226	-234.467820	-234.467503	-234.477332
Ci 1,5-hexadiene	DFT B3LYP/6-31G(d)	298.15	-234.469226	-234.461969	-234.461025	-234.500386
Ci 1,5-hexadiene	DFT B3LYP/6-31G(d)	400.00	-234.469226	-234.457169	-234.455903	-234.514584

Table 7: Summary of energetic values from a frequency analysis of C_i 1,5-hexadiene optimized at DFT B3LYP/6-31G(d) level at varying temperatures.

The first energetic energy value (E) is the intrinsic potential energy at 0K including quantum-mechanical zero-point vibration energy, the second is the energy at 298.15K and therefore is the sum of the first energetic value , E, and kinetic energy E_kinetic, which is the sum of rotational, vibrational and translational energies at room temperature. Sum of electronic and thermal enthalpies improve the energy correction further by including RT. Finally, the sum of electronic and thermal free energies account for entropic contributions. Calculations were performed for the optimized C_i 1,5-hexadiene on 100 K, 298.15 K and 400K (by changing the input gif files for each trial) which shows a trend of increasing sum of electronic and thermal energies owing to increased kinetic energy. As expected, the sum of electronic and thermal free energies increased along with temperature due to higher entropic contributions.

Nf710 (talk) 14:26, 21 January 2016 (UTC) Well done for doignit at different temperatures

Optimizing the "Chair" and "Boat" Transition Structures of Cope Rearrangement

In this section, the transition structures will be optimized to derive the most likely reaction pathway for Cope Rearrangement by first optimizing allyl fragments at the HF/3-21G level of theory. This is achieved using TS(Berny), freezing coordinates and Synchronous Transit-Guided Quasi-Newton (STQN) methods. The successes of these calculations are determined by the presence of an imaginary vibrational frequency and a small RMS gradient (signifying energy maxima in the PES surface).

All methods of calculating the transition structure require a starting geometry and initial estimate of the Hessian, which are then subsequently updated at each step of the reaction progress.

Optimizing the Allyl Fragments

CH₂CHCH₂ fragment was built and optimised to a minimum using HF/3-21G level of theory. The results are tabulated here:

Structure	Level of Calculations	Total Energy (a.u.)	Log file source
Allyl Fragment	HF/3-21G	-115.82303995	File:ALLYL FRAGMENT.LOG

The optimised allyl fragment will be used for building subsequent transition structures.

Using TS(Berny) For Chair Transition State Optimization

The assumption of using TS(Berny) calculation is that the guessed transition structure is accurate enough to compute the force constant matrix. To perform TS(Berny) calculations, the allyl fragment is duplicated and symmetrized. Unlike normal optimization process for other structures, the transition state structure requires precise geometry for the reactants as to ensure that there is a negative curvature in the reaction coordinate. Calculations must ensure that the starting structure has only one negative eigenvector so that the guessed structure can converge to the closest saddle point. As a result, the terminal ends of the allyl fragments are set at 2.2 ‎Å apart, with C₁ symmetry for the entire structure. The results are tabulated here:

Structure	Level of Calculations	Total Energy (a.u.)	Imaginary Vibrational Frequency (cm-1)	Log file source
Chair T.S of Cope Rearrangement	HF/3-21G	-231.61932227	-817.87	File:TSOPTIMIZATION.LOG

Vibrational frequency is expressed as:

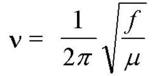
And therefore, an imaginary frequency must arise from a negative force constant, f. Imaginary vibrational frequency results from negative eigenvalues of the Hessian, which is a force constant matrix. In most normal modes of frequency that are positive for ground state structures, due to the fact that the potential energy surface curves upwards at all directions. However, at the saddle point, the energy reaches a maximum in one direction while being a minimum in all other directions. As a result this difference, the force constant acts in the opposite direction for transition structures, leading to an imaginary vibrational frequency. An animation of the imaginary vibrational frequency shown on the transition state optimization is visualized below:

Animation of imaginary frequency of the chair transition state via TS(Berny) at -817.87 cm-1

Using Frozen Coordinate Method For Chair Transition State Optimization

Unlike the TS(Berny) method, the Frozen Coordinate Method first optimizes the rest of the structure that are not involved in the bond breaking and bond forming sites using HF/3-21G level of calculations. Subsequently, the coordinates of the bond breaking/forming sites are changed to 'derivatives', which would reflect the optimization of the inter-fragment distances leading to the transition state. In order to build the input structure, the initial inter-fragment distances are set to be 2.2 ‎Å.

Structure	Level of Calculations	Total Energy (a.u.)	Imaginary Vibrational Frequency (cm-1)	Log file source
Chair T.S of Cope Rearrangement	HF/3-21G	-231.61932198	-818.06	File:(D)OPT.LOG

Like the TS(Berny) calculations, the structure that is generated at the end of the optimization process is a transition state given the imaginary vibrational frequency.As shown below, the vibrational mode concerns the elongation and compression of the terminal carbons involved in the bond breaking/forming process and therefore represents the transition state towards the Cope Rearrangement.

Animation of imaginary frequency of chair transition state via frozen coordinate method at -818.06 cm-1

Summary of Optimizing Chair Transition State of Cope Rearrangement

Comparison between the two methods for optimizing the transition structure can be evaluated by the interatomic distance between the terminal carbons, which are the sites for the reaction.

Type of Calculations	Interfragment Bond Length (‎Å)
TS(Berny)	2.02039
Frozen Coordinates	2.02172

As shown, the resultant geometries of the transition state using both methods are very similar, with bond lengths accurate to 10^-2 ‎Å. Furthermore, the difference in the final total energy is also appreciably small, 0.00000029 Hartrees or ~0.000182 kcal/mol. From these results, it is reasonable to conclude that both methods produce the same structure at the same saddle point on the PES surface, which is the chair transition state. Close approximation to empirical results is possible for simple molecules due to simpler geometry involved in the process (the initial geometry is an important factor for the TS(Berny) calculations).

Using the QST2 Method For Boat Transition State Optimization

The boat transition structure will be optimized using quadratic synchronous transit (QST2) method at HF/3-21G level of calculations. For the minimization process, QST2 method uses redundant internal coordinates as well as Newtonian laws to complete the optimization process. It operates by searching for a maximum along the quadratic region of the PES surface and minimum in all directions perpendicular to the curve that connect products with reactants. As a result, the calculations are performed using the optimized reactant and product shown below:

To be interpolated: optimized reactant (left) with optimized product (right)

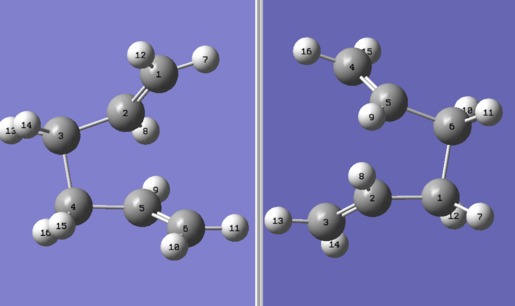
Calculations are performed using the C_i molecule optimized in the earlier section. Given the mechanisms of Cope rearrangement, corresponding carbon atoms in the reactants and products need to be labelled to reflect the rearrangement process. For example, the single bond between C3-C4 in the reactant will be broken to form a double bond between C2-C3 or between C4-C5. Similarly, another single bond needs to be formed between C1-C6, and hence a new carbon backbone is defined in the product. In addition to this, the structures of reactant and product need to be altered to resemble the transition state more closely. This involves changing the central C-C-C-C dihedral angle to 0^o and then changing the C2-C3-C4 and C3-C4-C5 dihedral angles to 100^o. The results calculated are tabulated below:

Structure	Level of Calculations	Total Energy (Hartrees)	Imaginary Vibrational Frequency (cm-1)	Log file source
Boat T.S of Cope Rearrangement	HF/3-21G	-231.60280201	-840.81	File:QST2 TRIAL2.LOG

The presence of an imaginary vibrational frequency again validate that the transition state has been reached. Animating this particular vibrational frequency indicates that as the distance between C3-C4 lengthens, C1-C6 distance is compressed.

Animation of imaginary frequency of the boat transition state at -840.81 cm-1

The Intrinsic Reaction Coordinate for the Chair Transition State

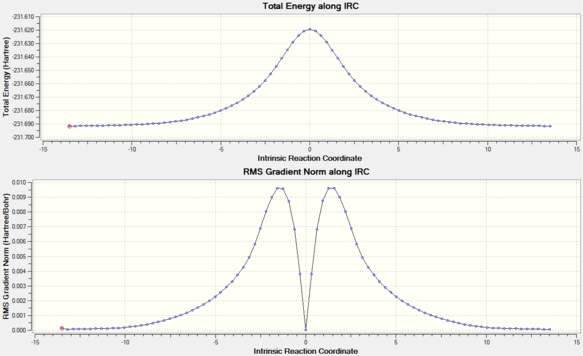
Prediction of the final conformers is hard to visualize using the transition structure, and as a result, the intrinsic reaction coordinate allows the transition structure to be transformed to a structure corresponding to a local minimum on the PES surface. The IRC, which is defined as the path to a transition state point from a stable equilibrium point, is generated using the initial geometry corresponding to the transition state and initial force constants and therefore consider nuclei movement with infinitesimal velocities. For this calculation, the reaction coordinate is computed in both directions and that the force constant is calculated at every step (this indicates that after every step, the force is re-evaluated to find the steepest gradient to a new position along the PES surface). A step of 100 IRC steps is performed, which yields the following reaction coordinate, shown below. Using the IRC calculations, it is shown that the final conformer is gauche2, with C₂ symmetry point group.

Number of Steps	IRC Path	Final Conformer	Final Conformer Total Energy (a.u.)
100	IRC path evaluated at 100 points for the Chair Transition State of 1,5-hexadiene during Cope Rearrangement	Gauche 1,5-hexadiene - gauche2	-231.69158000
125	IRC path evaluated at 125 points for the Chair Transition State of 1,5-hexadiene during Cope Rearrangement	Gauche 1,5-hexadiene - gauche2	-231.69158000

The IRC path shows that the calculations start from the transition state, the maxima point (labelled '0' on the Intrinsic Reaction Coordinate x axis) and possesses both directions to a constant minimum energy. Generally, the accuracy of IRC calculations depend on the number of points to be sampled until the final state is reached (final energy remains constant). Comparison between the 100 points and 125 points results indicated that the final conformer energy has remained constant, -231.69158000 a.u., and therefore 100 points for IRC calculations is sufficient. Apart from imaginary vibrational frequencies, the presence of transition structures can be verified using the RMS gradients, which are derivatives of the energy curve (a maxima or minima would lead to a gradient very close to 0).

Nf710 (talk) 14:28, 21 January 2016 (UTC) Correct conformer identified

Cope Rearrangement Activation Energies

The HF/3-21G optimized transition structures are re-optimized using the DFT theory, also producing the expected imaginary frequency vibration shown below:

B3LYP/6-31G(d) re-optimized chair transition state	B3LYP/6-31G(d) re-optimized boat transition state
Animation of imaginary frequency	Animation of imaginary frequency

	HF/3-21G			B3LYP/6-31G(d)
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0K	at 298.15K		at 0K	at 298.15K
Chair TS	-231.619322	-231.466700	-231.461340	-234.55693	-234.414910	-234.408982
Boat TS	-231.602802	-231.450915	-231.445288	-234.54308	-234.402356	-234.396012
Reactant (anti2)	-231.692535	-231.539539	-231.532566	-234.611613	-234.469226	-234.461969

Table 8: Summary of optimization results using different levels of theory and structures.

The structures are first optimized at HF/3-21G level; the output of which are then re-optimized at the DFT level, at B3LYP/6-31G(d) level, in order to maximize the accuracy of the structures' energies. Table 5 illustrates that optimization + frequency calculations performed for the three structures, so that the thermochemistry results can be derived. By comparing either the zero-point energies or the 298 K - corrected temperatures between the ground state reactant with a transition state, the activation energy can be derived.

	HF/3-21G	HF/3-21G	B3LYP/6-31G(d)	B3LYP/6-31G(d)	Experimental
	0K	298.15K	0K	298.15K	0K
Eact (Chair)	45.94	44.69	34.08	33.25	33.5 ± 0.5
Eact (Boat)	56.19	54.77	41.96	41.38	44.7 ± 2.0

Table 9: Comparison between the activation energies using different levels of theories and temperatures (all energy values in kcal/mol) Activation energies at lower temperatures are shown to be higher primarily due to the lack of thermal energies to reduce the activation barrier. As shown on Table 9, calculations involving the DFT B3LYP/6-31G(d) level results in activation energies closer to experimental results, while HF/3-21G results in transition states that are not as extensively optimized, leading to an increased energy gap between the ground state reactant to both transition states (higher activation energies). As mentioned in previous sections, the Hartree Fock method has compensated the complexity of multi-electron wave function by using one-electron wavefunction and therefore single Slater determinants that resulted from the Schrodinger equation also exclude Coulombic correlations. This energetic difference from actual values produced higher activation energies for the HF-optimized structures. However, both calculations showed that the activation barrier to a chair transition state is more energetically favourable.

The conformations/geometries of either transition state converges upon re-optimization. This is shown below, where the corresponding bond lengths do not alter significantly from HF to DFT calculations.

		HF/3-21G	B3LYP/6-31G(d)
Boat T.S	Allyl fragments separation (‎Å)	2.13767	2.20639
	Allyl C-C Bond (‎Å)	1.38176	1.39327
Chair T.S	Allyl fragments separation (‎Å)	2.02055	1.96470
	Allyl C-C Bond (‎Å)	1.38922	1.40791

Table 10: Comparison between the resulting geometries from optimizing each transition structure using both DFT and HF methods.

Table 10 illustrates that using either method does not prevent the transition states from converging to the final, most stable geometry, given the small differences (~of 10^-11 magnitude). As a result, a reasonable conclusion is that performing calculations at the expense of greater computational time does not necessarily impact geometries' convergence, but do affect energies more significantly, as shown by activation energies' discrepancies using either the chair or the boat transition state.

Nf710 (talk) 14:31, 21 January 2016 (UTC) Your energies are correct. you have made a very good report. you have shown an excellent understanding of the knowledge also and done pretty much everything that was asked of you.

Diels-Alder Cycloaddition: Ethene and cis-butadiene

[4n+2]π electrocyclic reaction

Introduction

This section investigates the transition structures involved in the formation of exo- and endo- products from a Diels-Alder cycloaddition between ethene and cis-butadiene using semi-empirical level of calculations. The AM1 calculations is a subclass of the semi-empirical method and serves as an improvement to the more time-consuming Hartree-Fock method, as it now accounts for electronic correlations through Modified Neglect of Diatomic Overlap while relying on empirical data on some of the calculations' parameters. All calculations performed uses the AM1 semi-empirical molecular orbital method, which uses modified expression for nuclear-nuclear core repulsion. In general, the semi-empirical models are based on neglecting diatomic differential overlap, such that the Hartree-Fock secular equation can be simplified. The merits of using semi-empirical methods included the consideration of actual experimental results in the parameterization for conventional systems to reduce computational time required; this differs from ab initio methods where a basis set is used in the Schrodinger equation.

Optimization of the reactants

To achieve the transition state for the Diels-Alder cycloaddtion , each of the reactant component is first optimized using the semi-empirical method. Cis-butadiene is built and optimized using AM1 semi-empirical method, with the following results:

Structure	Level of Calculations	Results Summary	Point Group	Final Total Energy (a.u.)	Log File Source
Cis-butadiene	AM1 semi-empirical method		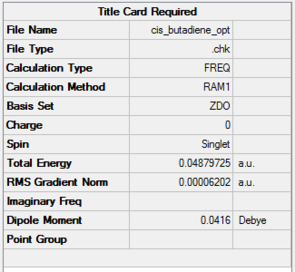C2V	0.04879725	File:CIS BUTADIENE OPT.LOG

The HOMO and LUMO of the optimized cis-butadiene are visualized below:

HOMO Molecular Orbital	LUMO Molecular Orbital
HOMO Molecular Orbital of optimized cis-butadiene showing antisymmetry with respect to the plane	LUMO Molecular Orbital of optimized cis-butadiene showing symmetry with respect to the plane

Similarly, ethene is built and optimized using the semi-empirical AM1 method, resulting in the following:

Structure	Level of Calculations	Results Summary	Point Group	Final Total Energy (a.u.)	Log File Source
Ethene	AM1 semi-empirical method		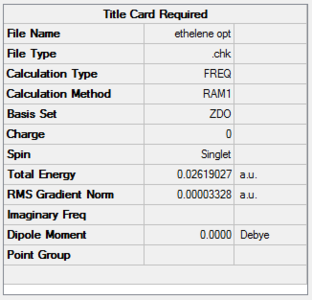D2h	0.02619027	File:ETHELENE OPT.LOG

The HOMO and LUMO of the optimized ethene are visualized below:

HOMO Molecular Orbital	LUMO Molecular Orbital
HOMO Molecular Orbital of optimized ethene showing symmetry with respect to the plane	LUMO Molecular Orbital of optimized ethene showing antisymmetry with respect to the plane

Optimization of Diels-Alder Transition State: Cis-butadiene and Ethene

Similar to the Cope Rearrangement, the Diels-Alder cycloaddition involves an envelope-type transition structure, The input file for the optimization process is generated by guessing a transition structure as per TS(berny) method. This is achieved by appending the optimized reactant molecules onto the same Gaussview window; the guessed structure is then symmetrized and the inter-fragment distances are set at 2.27 Å apart (this corresponds to literature value for this transition structure's geometry). The importance of initial geometry is again emphasized given the TS(Berny) method requires close approximation to the saddle point so that the initial forces can allow the input structure to arrive at the transition state. Running calculations using AM1 semi-empirical method results in:

Structure	Level of Calculations	Results Summary	Final Total Energy (a.u.)	Imaginary Vibrational Frequency (cm-1)	Log file source
Guessed transition structure	AM1 semi-empirical		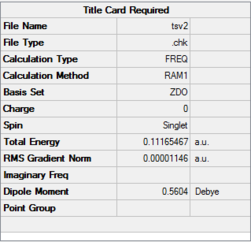0.11165467	-956.14	File:TSV2.LOG

Presence of an imaginary frequency, -956.14 cm^-1, confirmed that this is a transition state; the vibration motion at this frequency is visualized below:

Animation of imaginary frequency at -956.14 cm-1	Animation of first positive frequency at 147.05 cm-1

The imaginary vibrational frequency shows that the terminal carbons of each fragment compresses and elongates simultaneously for both pairs, and therefore the C-C bond formations can be considered to be synchronous. As a result of this motion, the breaking of C=C double bonds are also simultaneous, indicating that the pericyclic mechanism is concerted instead of a stepwise process. 147.05 cm^-1 is the lowest positive frequency, which shows that the ethene fragment twists asynchronously with the cis-butadiene fragment, but does not show a compression or elongation of the fragment distances. This suggests that this vibrational frequency is not involved in the bond forming process. As mentioned in the previous sections, only the negative vibrational frequencies correspond to the transition state, given that forces at all directions except for one are positive.

Geometry of the Transition State

	C5-C11 Bond Length- Partly formed C-C σ bond (Å)	C7-C14 Bond Length - Partly formed C-C σ bond (Å)	C3-C5 Bond Length (Å)	C11-C14 Bond Length (Å)
Optimized transition structure labelled	2.11918	2.11940	1.38186	1.38290

Table 11: Calculated geometries of the optimized transition structure using the semi-empirical AM1 method and minimized to TS(Berny).

Literature Values	Å
C5-C11 Bond Length-Partly formed C-C σ bond	2.27
C7-C14 Bond Length-Partly formed C-C σ bond	2.27
C3-C5 Bond Length	1.38
C11-C14 Bond Length	1.39

Table 12: Literature values of bond lengths within the transition structure, computed using B3LYP/6-31G(d) level

As shown, there are minor differences in the derived geometries between the structures from the semi-empirical method with the DFT method, but the percentage differences are very small. The largest difference results from the inter-fragment distance, which could result from varying the initial geometry of the guessed transition state. Sp³ hybridized C-C sigma bond is approximately 1.54 ‎Å, while sp2 hybridized C=C double bond is 1.20 Å. Comparisons with Table 6 illustrate that the double bonds in the optimized transition structure are still very similar to the expected C=C bond length (15% percentage diddference) and therefore, the transition state is 'early', resembling the reactant structure more than the product. Looking specifically at the partly formed C-C σ bonds, the reaction has progressed from the initial guessed transition structure where the C-C bond distance was 2.27 Å. As a result, there is evidence of attraction between the ethene and butadiene frameworks to form the sigma bond, while the double bonds are breaking synchronously in the cis-butadiene fragment, owing to the 15% difference between the literature bond lengths and the final structure. The Van-der-Waals radii of a carbon atom is 1.77 Å, and therefore considering that the partly formed C-C σ bond is shorter 2x(Van der Waals radii) indicate that there is increased overlap between the carbon atoms to start forming the C-C bonds at these positions. This strongly suggests bond interactions between the two reactants while the imaginary frequency verifies that the vibration mode contributes to the formations of these bonds.

Molecular Orbitals of the Transition State

HOMO of optimized transition structure	LUMO of optimized transition structure
HOMO of the transition state showing antisymmetry with respect to the nodal plane.	LUMO of the transition state showing symmetry with respect to the nodal plane.

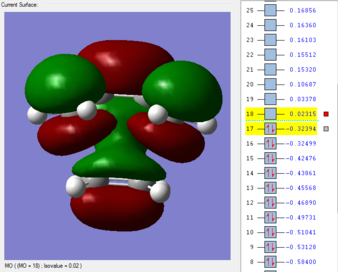
The HOMO of the transition state is antisymmetric with respect to the nodal plane, and the LUMO of the optimized transition structure is symmetrical to the nodal plane. Owing to the symmetry rule in combining orbitals, symmetrical orbitals combine to form symmetrical molecular orbitals and a combination of asymmetrical and symmetrical orbitals combine to form antisymmetrical molecular orbitals. Comparing to the HOMO/LUMO structures of the reactants, the HOMO of the optimized structure is shown to be the overlap between the antisymmetrical HOMO of cis-butadiene and the antisymmetrical LUMO of ethene. This corresponds to the overlap between the π molecular orbitals of butadiene fragment and the π^* molecular orbital of ethene.

This particular Diels-Alder reaction involves 4+2 pi electrons electrocyclic reaction, and therefore according to Woodward-Hoffmann rules, constructive overlap occurs when the butadiene adopts a conrotatory approach with the ethene given that the outermost p-orbitals of the hexadiene are of opposite signs.

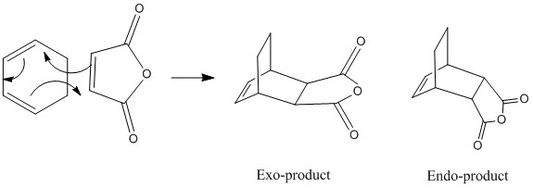
Analysis of Regioselectivity in Diels-Alder Reaction: Maleic Anhydride and Cylohexadiene

Reaction mechanism illustrating regioselectivity in Diels-Alder Cycloaddition

Introduction

The transition structure is built after optimizing each of the reactant structure using the sem-empirical method at the AM1 level, which are then appended to the same Guassian window. Each of the exo or the endo transition state are first optimized to a minimum using semi-empirical methods, before optimized using TS(Berny) method. In the Diels-Alder reaction, there is a competition between the endo and exo products, where the exo product is the stable thermodynamic product and the endo product is the faster-formed kinetic product. Due to the cyclic nature of the diene, there are two competing pathways at which maleic anhydride can approach the diene, which arise from a combination of steric and electronics factors shown below.

Optimization of the reactants

Optimization of maleic anhydride yields the following results:

Structure	Level of Calculations	Calculations Results	Point Group	Final total energy (a.u.)	Log file source
Maleic anhydride	AM1 semi-empirical		C2V	-0.12182418	File:REACTANT2 OPT.LOG

Table 13: Optimization results for maleleic anhydride using semi-empirical AM1 method.

Structure	Level of Calculations	Calculations Results	Point Group	Final total energy (a.u.)	Log file source
Cyclohexa-1,3-diene	AM1 semi-empirical		C2	0.02771132	File:REACTANT1 OPT.LOG

Table 14: Optimization results for cyclohexa-1,3-diene using semi-empirical AM1 method.

HOMO of Maleic Anhydride	LUMO of Maleic Anhydride

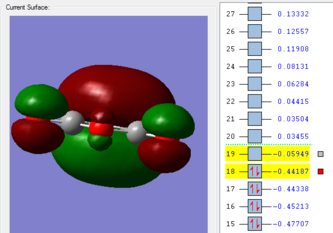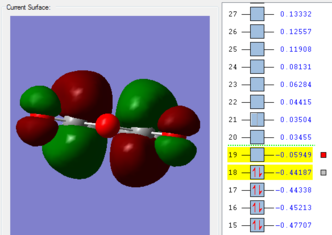HOMO of Cyclohexa-1,3-diene	LUMO of Cyclohexa-1,3-diene

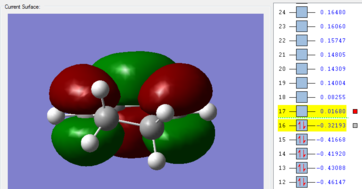The HOMO of maleic anhydride is antisymmetrical to the nodal plane, while the LUMO of maleic anhydride is symmetrical to the nodal plane. On the other hand, the LUMO of cyclohexa-1,3-diene is antisymmetrical to the nodal plane and the HOMO of cyclohexa-1,3-diene is symmetrical to the nodal plane.

(I think it's the opposite symmetry for all four Tam10 (talk) 15:19, 12 January 2016 (UTC))

Analysis of the endo/exo transition structures

The transition structure is built by first visualizing the final exo and endo products and then subsequently removing the resultant C-C sigma bonds, "cleaning" the structure and then symmetrize the transition structures before optimization. In addition, the two reactants' bond-forming sites are separated by 2Å. Given that the method of calculation used is TS(Berny), there is a requirement that the guessed transition structure needs to be reasonably close to the PES saddle point, and to ensure that the structure is built as realistic as possible, a minimum optimization is performed first for each reactant.

The calculations for the minimized transition structures are shown below:

Structure	Level of Calculations	Calculations Results	Final total energy (a.u.)	Imaginary Vibrational Frequency (cm-1)	Log file source
Endo transition structure	AM1 semi-empirical		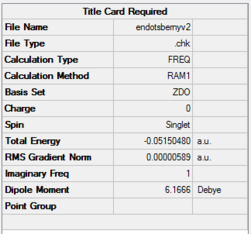-0.05150480	-806.49	File:ENDOTSBERNYV2.LOG
Exo transition structure	AM1 semi-empirical		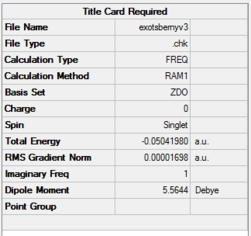-0.05041980	-812.23	File:EXOTSBERNYV3.LOG

Table 15: Guessed transition structures optimized to TS(Berny) using AM1 semi-empirical method

Animation of imaginary frequency of the endo transition state at -806.49 cm-1

Frequency analyses of the completed transition structures illustrate imaginary vibrational frequencies and therefore verified that endo and exo transition structures are formed in their respective simulations. The animation shown above for the endo transition structure shows that -806.49 cm^-1 corresponds to the formation of new C-C σ bonds in a synchronous manner. Similarly, the exo transition state also shows synchronous formation of the new C-C σ bonds, as well as the resultant double bond vibrates simultaneously in this frequency. A larger-in-magnitude vibrational frequency within the exo transition structure is indicative of a larger force towards the formation of the C-C σ bonds as vibrational frequencies are proportional to the force constants. Similarly, an imaginary vibrational frequency of -812.23 cm^-1 is observed for the optimized exo transition structure, which again verifies that the structure is a transition state. This vibration, animated below, also illustrates the synchronous formation of two new C-C σ bonds.

Animation of imaginary frequency of the exo transition state at -812.23 cm-1

The computed final energies of the transition structures correspond with expected theoretical results where the endo transition structure would correspond to a lower activation energy, due to stabilising secondary orbital interactions between the π systems of the alkene functionality from cyclohexa-1,3-diene and maleic anhydride, in addition to the lack of steric clash between the -CH₂CH₂- fragment with the maleic anhydride. Converting to kcal/mol, the energy difference between the transition structure is 0.681 kcal/mol according to AM1 semi-empirical calculations. In regards to energetic differences, orbital interactions are primarily responsible for favoring the endo transition state while the steric repulsion disfavors the exo transition state.

The extent of steric repulsion can be seen through the space and bond distances within both structures:

Endo Transition State labelled	Exo Transition State labelled

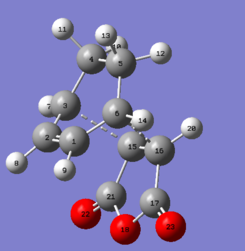	Transition State (‎Å)
C3-C15 Bond Distance	2.16236
C6-C16 Bond distance	2.16234
C1-C2 Bond Distance	1.39723
C3-C4 Bond Distance	1.49052
C15-C16 Bond Distance	1.40849
C5-C17 Space Distance	3.89681
C4-C21 Space Distance	3.89668

Table 16: Geometry of the optimized endo transition state

	Transition State (A‎)
C3-C15 Bond Distance	2.17046
C6-C16 Bond distance	2.17029
C1-C2 Bond Distance	1.39677
C3-C4 Bond Distance	1.48981
C15-C16 Bond Distance	1.41010
C5-C17 Space Distance	2.94510
C4-C21 Space Distance	2.94503

Table 17: Geometry of the optimized exo transition state

Both transition states show a progression from the reactant structure as the initial fragment distances have shrunk to 2.16-2.17 Å, while the partly broken C-C double bond lengths in the cyclohexa-1,3-diene component have lengthen to 1.49 Å, which only accounts for 3% difference from the expected sp³ C-C bond lengths. It is also important to note that the partly formed C-C σ bonds are shorter in the endo transition state, which suggests a more advanced progression towards the product. This again suggests electronic effects that would enhance the attraction between the O=C-O-C=O fragment and the double bond fragment (an analysis of orbital overlap in later section would indicate that secondary orbital overlap is responsible).

The similar bond distances for the partly formed C-C sigma bonds are also indicative of a synchronous formations of new bonds in the transition structure. In addition, from the initial configuration, the bond distances around the cyclic ring are between c-C single and double bond, which suggests that original pi-bonds are breaking as new pi bond between C₁-C₂ are forming.

As expected, the steric repulsion is pronounced for the exo transition state, given that the endo transition structure's space distances between the O=C-O-C=O fragment and the -CH₂CH₂- fragment are 32% larger than those of the exo transition state. This is shown again by the fact in the exo transition state, C₅-C₁₇ space distance is larger than the sum of carbon atoms' Van der Waal's radius. On the other hand, the same space distance for endo transition state is 3.89Å, which is sufficiently larger than 2x(carbon Van der Waal's radii) to justify a lack of steric repulsion. In summary, the relative stability of the endo transition state can be attributed to a combination of sterics effects, shown by the space distances between the fragments, and electronic effects (primarily the secondary orbital overlap effect as evidenced in the next section). Determining the exact contribution of either secondary orbital overlap effect in endo structure and steric clash in exo structure has been a topic of research; but more recently, literature research has cited that steric arrangements play a greater role in endo selectivity, as opposed to orbital interactions.

("in the exo transition state, C₅-C₁₇ space distance is larger than the sum of carbon atoms' Van der Waal's radius" - do you mean smaller? Tam10 (talk) 15:19, 12 January 2016 (UTC))

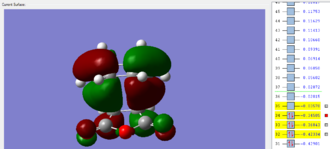
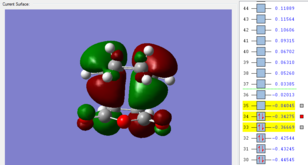
Primary and Secondary Orbital Overlaps

HOMO (Endo Transition Structure)	LUMO (Endo Transition Structure)	HOMO (Exo Transition Structure)	HOMO (Exo Transition Structure)

Endo transition structure: observed secondary orbital overlap between π framework and oxygen atoms' p-orbitals.

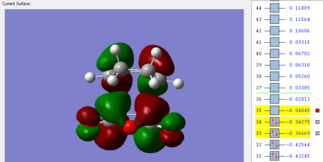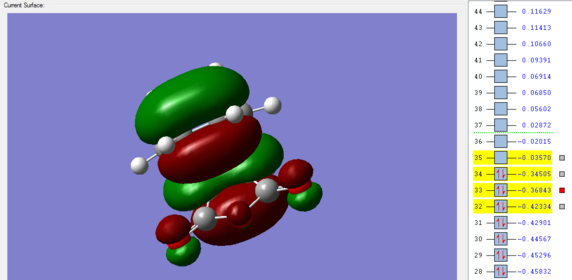
The HOMO and LUMO of the endo transition structure are both antisymmetrical with respect to the nodal plane. Similarly, the HOMO and LUMO orbitals of the exo transition structure also exhibit antisymmetry with respect to the nodal plane. Unlike primary orbital overlaps, secondary orbital overlap is defined as the bonding interaction of non-participating fragments (or areas where no bond changes are observed in the transition state). In the case of the endo transition structure, this is shown to be the overlap between the p-orbitals of the oxygen atoms with the pi-system of the cyclohexa-1,3 diene (the molecular orbital is second highest occupied molecular orbital). This is only observed in the endo transition structure, as the orientation of maleic anhydride allows non-bonding p orbitals to align with the π system of cyclohexadiene.

Given that this particular molecular orbital is doubly populated, there is increased stabilization for the entire system when orbitals overlap to form the transition state and therefore stabilizes the structure relative to the exo transition state.Primary orbital overlaps are present in both transition structures, and therefore exo product can still be expected to form, but will be the minor product, as the pathway towards endo product will be faster. As a result, the secondary orbital overlap effect and lack of steric repulsion have made the endo transition structure more kinetically favorable.

Intrinsic Reaction Coordinate and Activation Energies

At 298.15K IRCs paths are generated for each transition state using 24 steps for the exo transition state and 20 steps are performed for the endo transition state. Both reaction coordinates shows complete pathway to their respective products. For the IRC calculations, the reaction is run in both directions (Transition state to products as well as transition state to reactants) given that the reaction profile is not symmetrical as compared to Cope rearrangements. As shown below, the endo transition state leads to a product that is much higher in energy than in the case of the exo pathway. This again validates the observation that the exo-product is thermodynamically favored due to a higher activation energy as compared to the endo-pathway.

Intrinsic Reaction Coordinate Exo Transition State	Intrinsic Reaction Coordinate Endo Transition State

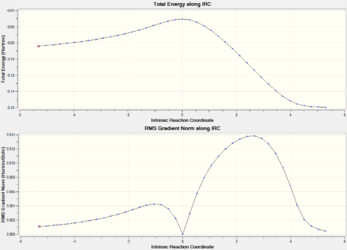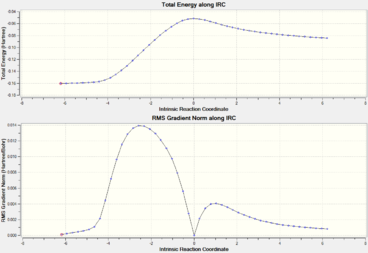The reaction coordinate suggests that exo transition state leads to the more stable product as compared to the endo transition state. However, given the significant stabilization of the endo transition state due to lack of steric repulsion, as well as the fact that the endo transition state also exhibit the required primary orbital overlap to form the Diels-Alder adduct, more of the endo-products are formed due to faster rate. In accordance to the Arrhenius equation, a faster rate must imply a smaller activation energy, which is evidenced below:

	Electronic Energy (a.u.)	Sum of electronic and zero-point energies (a.u.)	Sum of electronic and thermal energies (a.u.)
		at 0 K	at 298.15 K
Exo Transition State	-0.05041980	0.134881	0.144882
Endo Transition State	-0.05150480	0.133494	0.143683
Maleic Anhydride	-0.12182418	-0.063346	-0.058192
Cyclohexa-1,3-diene	0.02771132	0.152502	0.157727

Table 18: Summary of energies for all structures involved in the Diels-Alder reaction

	at 0 K	at 298.15 K
EAct (Exo Transition State)	28.69285	28.45565
EAct (Endo Transition State)	27.82249	27.70327

Table 19: Activation energies via varying reaction pathways (in kcal mol^-1)

Table 19 verifies again that the cycloaddition between maleic anhydride and cyclohexadiene has a energetic preference to form endo transition state rather than the exo tranistion state, given the difference in activation energy accounting for 0.752383 kcal/mol at normal conditions.

Conclusions

In conclusion, this exercise had derived the lowest conformer of 1,5-hexadiene using Hartree-Fock method at the 3-21G basis set. Calculations to find the lowest-energy conformer has defied theoretical expectation by illustrating that in the gauche conformer, there is observed orbital overlap between the two π systems in the reactant, which is non-detectable in the anti-periplanar conformer. The reliability of using lower basis set was evaluated by optimizing the antiperiplanar conformer of 1,5-hexadiene using DFT and HF methods. In regards to the final geometry of the transition structure, the DFT method has shown to be more reliable, giving bond lengths that fit with literature values, which again suggests that the use of electron densities to approximate chemical properties may be more accurate compared to the 3-21G basis set. This is especially evident in deriving correct energies, as HF/3-21G's reliance on single-determinant approach produces larger margin of error.

Using HF/3-21G pre-optimized allyl fragments, the 'chair' and 'boat' transition states involved in the Cope rearrangement are optimized using TS(Berny) method, the frozen coordinate method and the QST2 method. For the chair transition structure of the Cope Rearrangement, the final electronic energies and the inter-allyl fragments' distances calculated by guessing the structure versus frozen coordinate method are reasonably similar, which suggests that the TS(Berny) method is suitable for calculating the transition structure involving simpler system as the initial guessed structure can easily be optimized to the actual saddle point on the PES surface. Again, the outputs are confirmed to be actual transition state by the presence of imaginary vibrational frequency that corresponds to the motion of the fragments in key bond formation process. In addition, by comparing the activation energies, it is shown that the DFT method operating at the 6-31G(d) basis set produced values closer to experimental values, and that the 'chair' structure requires smaller activation energy.

Subsequently, two diels-alder cycloaddition reactions are simulated: ethene with cis-butadiene, as well as maleic anhydride with cyclohexa-1,3-diene using semi-empirical AM1 method. The shift from ab initio method is justified due to the increase in structure complexity and therefore more computational resources can be conserved by using empirical results for selected parameters.In addition, the regioselectivity of Diels-Alder reaction was also studied by observing the endo and exo transition structures optimized using semi-empirical AM1 method. The final energetic values suggest that the endo transition structure is representative of the kinetic pathway. By analyzing the space distances between the O=C-O-C=O fragment and the -CH₂CH₂- fragment, the exo transition structure illustrates steric repulsion absent from the endo transition structure. In addition, the secondary overlap between π system of the diene with the non-bonding p orbitals of maleic anhydride has contributed to the relative stabilization of the endo transition state. A possible progression after this exercise is to compute the relative contribution of secondary orbital overlap effect versus the lack of steric repulsion towards the stabilization of the endo structure. This can be achieved by performing trials where the non-bonding orbitals of the dienophile are contracted so that secondary orbital overlap effects are subsequently minimized; more specifically, this would involve incorporating more electron-withdrawing groups on the dienophile so that orbital overlap is decreased in the endo transition state.