Tutorial – Cope Rearrangement

Cope rearrangement is a pericyclic reaction, more specifically [3,5] sigmatropic rearrangement of 1,5 dienes. Transition states of Cope rearrangement reaction of 1,5-hexadiene were studied in this tutorial with the aid of computational program Gaussian. Cope rearrangement of 1,5-hexadiene can proceed through chair or boat like transition states.

Optimizing Reactants and Products

In the first part of tutorial 1,5-hexadiene molecule was optimized so that its lowest energy point and symmetry was found. Then it was optimized further in order to find its vibrational frequencies and energies comparable with the experimental values.

1,5-hexadiene molecule with approximately anti-linkage between the middle four carbon atoms was drawn in GaussView. Structure was cleaned and then optimized to a minimum energy at the following level: HF/3-21G (Hartre-Fock with a basis set 3-21G). Energy of the optimized structure was found to be -231.69253528 Hartrees. With the use of symmetrize function in GaussView it was established that its symmetry is Ci. This structure corresponds to structure anti2 from Appendix 1 [1].

New molecule of 1,5-hexadiene was drawn, this time with gauche-linkage between the central four carbon atoms. Molecule was optimized at the same level of theory as the first molecule (HF/3-21G). It was expected that the energy of the gauche conformation would be higher due to steric clashes between the terminal vinyl groups. Energy of the optimised molecule was found to be - 231.69166701 Hartrees with the C2 symmetry which corresponds to gauche2. As predicted this conformation is higher in energy than anti by 8.6827 E-4 Hartrees.

The lowest energy conformer was expected to be the one with anti-linkage between the central four atoms of 1,5-hexadiene. To see if maybe a conformer with even lower energy than the one already optimized exists, new molecule was drawn with anti linkage and optimized at the same level of theory as before. Energy of the conformer was found to be – 231.69260237. This molecule had C2 symmetry. This is indeed lower in energy than the molecule with Ci symmetry.

Conformation	Structure	Energy	Symmetry	From Ap. 1
anti	ExampleR1C2	-231.6925353	Ci	anti2
anti	ExampleR2C2	-231.6926024	C2	anti1
gauche	ExampleR3C2	-231.6916670	C2	gauche2

Table 1 summarizes all optimized structures so far and their corresponding structures from Appendix 1. It was found that with this level of theory all the energies of optimized molecules are the same as those reported in Appendix 1.

Conformation with Ci symmetry was optimized further on the higher level of the theory. DFT was chosen as a method, B3LYP as functional and 6-31G* as basis set (shorter notation of these settings: B3LYP/6-31G*). Name of the output checkpoint file was changed under the Link 0 in order to preserve original checkpoint file from the optimization on the lower level of the theory. Energy of the optimized molecule was found to be -234.55970458 Hartrees. This differs from the energy obtained with HF/3-21G. Though it is not possible to compare the two because the underlying methods to calculate energies are different. The overall symmetry of the molecule did not change and remained Ci. (Even though the symmetry is conserved, are the structures similar? If one takes an ethene molecule an stretches the CC bond by 10Å, the symmetry group would be the same, but the structures would be significantly distinct. João (talk) 10:57, 24 March 2015 (UTC))

In order to get energies comparable to experimentally measured quantities a frequency calculation has to be done. This calculation also allows us to see if optimized molecule can exist and is in fact a minimum energy state (there are no negative vibrations). Conformer optimized on the B3LYP/6-31G* level of the theory has been used for frequency calculation. Frequency was chosen as Job Type, method was set to be B3LYP/6-31G*. When the calculation has finished .log file was opened in order to check that all vibrational frequencies were positive and to visualize calculated vibrations.

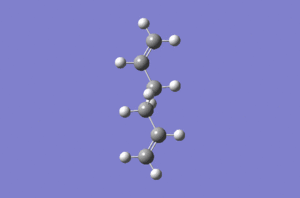
Thermochemistry information were taken from the output file and are presented in Table 2.

Energy: Sum of electronic plus	What does it represent...	Calculated values
zero point energies	potential energy at 0 K including zero-point vibrational energy	-234.416255
thermal energies	energy at 298.15 K, 1 atm including translational rotational and vibrational energies	-234.416255
thermal enthalpies	additional correction for RT	-234.408019
thermal free energies	entropic contribution to the free energy	-234.447872

Optimizing the "Chair" and "Boat Transition Structures

As mentioned before, the Cope rearrangement can proceed via boat or chair like transition structures. Both transition states were analyzed in this tutorial

Chair Transition Structure

Allyl fragment was drawn with the aid of GausView and optimized using the HF/3-21G level of theory. Optimized molecule was copied and pasted to new GaussView document twice (first time using Create MolGroup and second time using Append Molecule). Fragments were oriented so that the terminal carbons of both allyl fragments were approximately 2.2 Å apart. This structure was saved at guess structure for chair transition state and was then optimized in two different ways. Firstly the transition state was optimized directly, computing Hessian, from the guess structure. This method only works if the guess structure is already close enough to the real transition state structure. Second way of optimizing transition structure was with the aid of frozen coordinates. This method can bring some benefits, especially in terms of the time (there is no need to compute whole Hessian).

"Hessian Method"

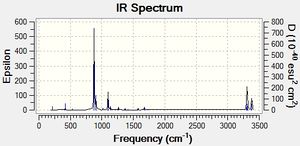
Guess structure was optimized at the HF/3-21G level of theory in the following way: Job type was set to Opt+Freq, and then Optimization to a TS(Berny) was chosen with force constant calculated once, Opt=NoEigen was added to the additional keyword box to stop calculation from crashing should more than one imaginary frequency be detected. When the calculation was completed successfully, vibrations were animated and IR spectrum was generated. It was confirmed that the vibration corresponds to Cope rearrangement with an imaginary frequency of magnitude 817,90 cm-1.

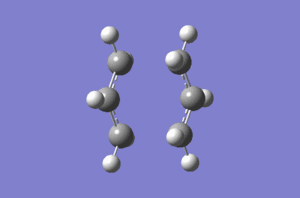
"Frozen coordinates" Method

Same guess transition structure was used for this, second, method of optimizing transition state. Under the Redundant Coord Editor in GaussView bond lengths of terminal carbon atoms of allylic fragments were set to be frozen at 2.2 Å (this was done with two separate inputs for each bond). Structure was then optimized to minimum at the HF/3-21G level of theory (Opt=ModRedundant was automatically included in the input line). After the optimization the coordinates were unfrozen and the option Derivative was used for both bonds under the Redundant Coord Editor. This command told the program not to compute the whole Hessian but just to differentiate along the reaction coordinate. Job was then set to Opt+Freq to TS(Berny) but without calculating force constant (option Never was chosen). As before Opt=NoEigen was added to the additional keywords box (Do you expect this keyword to be as important as before? João (talk) 10:57, 24 March 2015 (UTC)). When the calculation was completed transition state was visualized. The bond forming and breaking bonds were found to be 2.02028 Å and 2.02036 Å respectively. This is almost the same as with the direct method without frozen coordinates which means that even though the methods are different they lead to the same result.

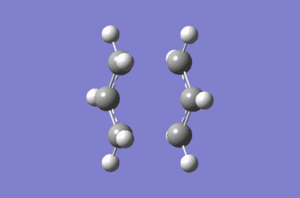
Boat Transition Structure

Boat transition structure was optimized using QST2 method. In this method both the reactants and the products are specified. Optimized structure of 1,5-hexadiene with the Ci symmetry was used for transition state simulation. Structure was copied to new window twice, the second time Add to MolGroup was used which created two separate inputs in the same window, in other words the program was told that one of the molecules was reactant and the other one product. Numbering of the atoms was adjusted so that it was exactly the same on both molecules. Then job was set to Opt+Freq and TS(QST2) was chosen from the menu.

The job completed successfully but on the inspection of the resulting transition stated it was seen that it looks the same as the chair transition state which means that there was only the translation of the top allyl fragment.

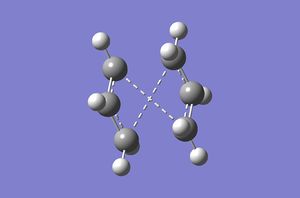
In order to get the desired boat transition structure, orientations of both molecules had to be modified. Dihedral angle between the central four carbon atoms was set to 0° and angle between second, third and fourth carbons from both sides was set to 100°. Same calculation as before was set. This resulted in desired transition state shown in FIgure X. energy of this transition state was -231.60280234 Hartrees, with and imaginary frequency at -839.79.

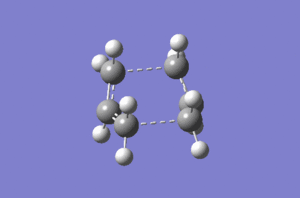
Intrinsic Reaction Coordinate

Method calle Intrinsic Reaction Coordinate can follow the minimum energy path from a transition structure to the local minimum on a potential energy surface. This calculation was done for chair transition state. IRC was chosen as the Job Type then following settings were applied: Forward Direction (because the reaction coordinate is symmetrical), Always for force constant and 50 for number of points along the IRC. Method was run on the HF/3-21G level of theory. Results obtained are shown in Figure X. It can be clearly seen that the minimum had not been reached (Why is it clearly not a minimum? João (talk) 10:57, 24 March 2015 (UTC)). Therefore the last structure was optimized again to the minimum energy on the same level of theory. Energy obtained was -231.69166702 and molecule had C2 symmetry. However this molecule does not represent the conformer with the minimal Energy from Appendix 2 (Is it not the gauche2 structure? João (talk) 10:57, 24 March 2015 (UTC)) probably because the minimum energy conformer can be found away from the minimum energy path.

Activation Energies of Both Conformers

Calculations were started from the optimized transition structure. They were optimized on the higher level of theory (B3LYP/6-31G*) and frequency calculations were carried out. Upon the comparison of the results it was found that the geometries of transition states optimized on the higher level of theory do not differ significantly from those optimized on the lower level of theory. However the energies differed quite significantly. (How do the activation energies differ? Which is the most favorable transition state? How do your results compare with experimental values? João (talk) 10:57, 24 March 2015 (UTC))

The Diels Alder Cycloaddition

In this section two different Diels Alder cycloadditions were investigated, first was the reaction between 1,3-butadeiene and ethylene, second was reaction between 1,3-cyclohexadiene and maleic anhydride. Semi-empirical AM1 level of theory was used for the calculations. Diels Alder reaction is pericyclic reaction between conjugated alkene (dienophile) and a substituted alkene. Generally the HOMO/LUMO of one fragment interacts with HOMO/LUMO of the other reactant. In this process two new σ bonds are formed. Reaction is allowed if HOMO of one molecule reacts with the LUMO of the other one. On the other hand reaction is forbidden if the orbitals interacting have different symmetry properties.

Reaction between ethylene and cis-buta-1,3-diene

Both molecules were drawn and optimized. HOMO and LUMO of both reactants were visualized. It can be seen from the visualized orbitals that they have the same symmetry as the molecule. HOMO orbitals are antisymmetric, and LUMO are symmetric. (What does it mean that orbitals have the same symmetry of the molecule and then one is symmetric and the other anti-symmetric? (With respect to what?) João (talk) 10:57, 24 March 2015 (UTC))

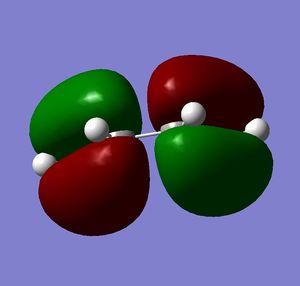
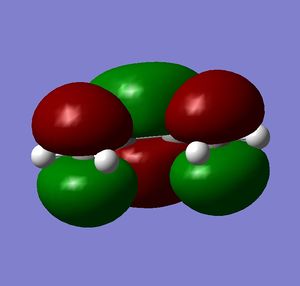
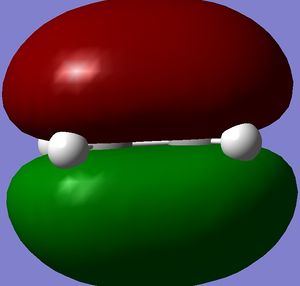
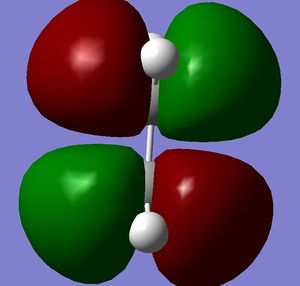
Then they were added together so that the bond forming distances were approximately 2.2 Å and the Opt+Freq calculation for TS(Berny) was run (Did you confirm it was a transition state? Is the bond formation synchronous? João (talk) 10:57, 24 March 2015 (UTC)). Orbitals of the transition states were visualized. LUMO of the transition state is symmetric and HOMO is anti symmetric (with respect to the reflection plane). Orbital symmetry in the reaction is therefore conserved and the reaction is allowed.

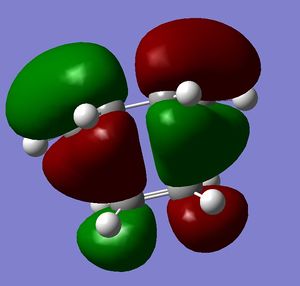
Study of regioselectivity of the Diels Alder Reaction

Cyclohexa-1,3-diene reacts with maleic anhydride to give endo adduct. Exo transition state is higher in energy because reaction is kinetically controlled (Reference? Do your results confirm this? João (talk) 10:57, 24 March 2015 (UTC)). Both reactant molecules were drawn and optimized. Transition state optimization was done using the frozen coordinates method (direct method was done but did not result in transition state because guess transition structure was too far away from the real one). HOMO and LUMO for both transition states were then visualized. There was no secondary orbital overlap seen in neither of the structures (What is the secondary orbital effect? João (talk) 10:57, 24 March 2015 (UTC)). From that it can be concluded that the endo transition state is more favorable because of the steric hindrance in the exo transition state (What kind of hindrance is there in the exo transition state? João (talk) 10:57, 24 March 2015 (UTC)) and not because of the secondary orbital overlap effect. Both HOMO and LUMO orbitals were determined to be symmetric which was expected because two symmetric molecular orbitals were mixed in the reaction. (Both orbitals you display are actually anti-symmetric with respect to the symmetry plane of the molecule. What reactant orbitals are involved in the formation of these orbitals? João (talk) 10:57, 24 March 2015 (UTC))

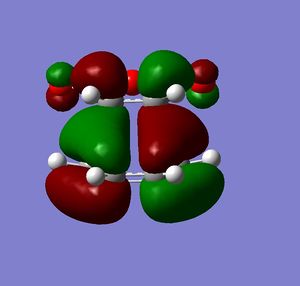
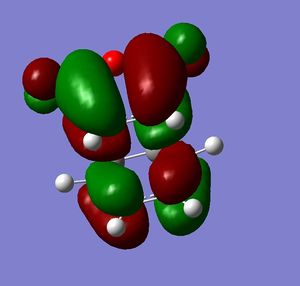
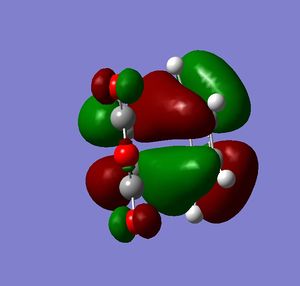
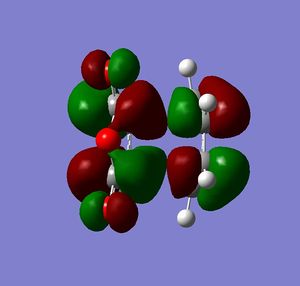
Typical sp3 C-C bond length is 1.54 Å, typical sp2 C-C bond length is 1.34 Å. [2] The Van der Waals radius of a C-atom is 1.72 Å [3]

Conclusion

All the experiments were successful in locating the transition states. Different computational techniques were met and tested as well as different levels of different theories. It can be concluded that the calculations obtained by theoretical methods go hand in hand with the experimental chemistry and are very useful to test and predict different theories.

References

[1] https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3#Optimizing_the_.22Chair.22_and_.22Boat.22_Transition_Structures

[2] G. Schultz, I. Hargitta, J. Mol. Struc., 1995, 346, pp. 63-69

[3] M. Mantina, A. C. Chamberlin, R. Valero, C. J. Cramer, D. G. Truhlar, 1995, 346, pp. 63-69