Module Three

In this investigation the transition states of the Cope rearrangement and Diels-Alder transition states are to be studied.

Cope Rearrangement

The Cope rearrangement is a [3,3] Sigmatropic shift reaction. It is a pericyclic reaction hence a concerted transition.

Optimising the Reactants and Products

a)

First an 1,5-hexadiene was drawn with an anti conformation, i.e. a central dihedral angle between the two carbon chains of 180^o. This structure was then optimised using HF 3-21g method and basis set. The total energy was noted and the point group worked out.

Anti 1

App

Total Energy -231.69253528 a.u.

DOI:10042/to-2862

Current point group Ci

You would expect the gauche conformation to be lower in energy to to the Gauche effect, this is the effect where the C-C sigma* orbital is stabilised by hypergonjugation from the app C-H sigma orbital. This usually has a greater stabilising affect than the destabilising steric clashes.

b)

Next another 1,5-hexadiene was drawn and optimised however this time instead of anti it was given a Gauche conformation, i.e. a central dihedral angle between the two carbon chains of 60^o.

Gauche 2

Gauche

Total Energy -231.69166701 a.u.

DOI:10042/to-2863

Current point group C2

This confomer is slightly higher in energy than the anti peri planar molecule above, this however is due to the app molecule being the second lowest in energy confomer. As will be shown bellow the lowest energy confomer is infact a gauche confomer.

c)

Gauche 3

Low Energy Gauche

Total Energy -231.69266121 a.u.

DOI:10042/to-2864

Current point group: C1

This confomer is the lowest energy 1,5-hexadiene possible, it has one Gauche twist stabilising the central C-C bond however the groups are as far away as possible inorder to lower steric clash.

d)

The structures drawn above correspond to the following confonmations in Appendix 1 of the exercise. Both the conformations and also energies agree with the table.

a) anti 1 b) gauche 2 c) gauche 3

e)

The Anti2 confomer was drawn and optimized using the same basis set and method as previously.

anti 2

Total Energy: -231.69253521 a.u.

Given energy: -231.69254 a.u.

Comparing the energy given from the calculation to the energy quoted in Apendix1 shows that the energies are the same, therfore the same confomer has been made.

Current point group: Ci

DOI:10042/to-2872

f)

The anti2 molecule was reoptimised, however using the stricter basis set and method of B3LYP/6-31G*

Total Energy(HF/3-21G): -231.69253521 a.u. Total Energy(B3LYP/6-31G*): -234.55970424 a.u.

There has been a segnificant reduction in energy after a more strict base set was used, a reduction of -2.8672 Hartree (-7527.834 kJmol^-1). This however is not a good representation in the actual change in energy as molecules calculated with different basis sets should not be compared.

Current point group: Ci

DOI:10042/to-2873

Bond Length / Angstroms
Bond	HF/3-21G	B3LYP/6-31G*
4-3	1.316	1.338
3-2	1.509	1.507
2-1	1.553	1.555
1-6	1.509	1.507
6-5	1.316	1.338

Bond Angle
Bond	HF/3-21G	B3LYP/6-31G*
4-3-2	124.81	125.21
3-2-1	111.35	112.65
2-1-6	111.35	112.65
1-6-5	124.81	125.21

Dihedral Angle
Bond	HF/3-21G	B3LYP/6-31G*
4-1	114.64	118.78
3-6	179.95	180.00
2-5	114.64	118.78

Although visually there is virtually no difference between the two on closer inspections of the bond angles, bond lengths and dihedral angles all of these have been adjusted slightly.

g)

A further calculation was run on the molecule, this time calculating frequencies.

When viewing the vibrational modes it was checked that there were no imaginary frequencies which would indicate that a minimum has not been reached but in fact a transition state.

DOI:10042/to-2877

i) Sum of electronic and zero-point Energies= -234.416244 a.u.

ii) Sum of electronic and thermal Energies= -234.408954 a.u.

iii) Sum of electronic and thermal Enthalpies= -234.408010 a.u.

iv) Sum of electronic and thermal Free Energies= -234.447849 a.u.

Optimising the "Chair" and "Boat" Transition Structures

In this section transition structure optimisations will be investigated using various computational methods.

a)

A CH₂CHCH₂ fragment was drawn in and optimised using HF/3-21G . The molecule was duplicated and manipulated to look like the chair conformation. The fragments were then set to be 2.2A apart.

b)

Using the two fragments created above a transition state optimisation and frequency was run, the basis set of 3-21G was used. instead of optimising to a minimum as done previously TS (Berny) was selected.

On inspection of the frequencies after completion, one imaginary negative frequency appeared. This frequency corresponds to the TS of the cope rearrangement. By visualising the vibration it can be seen that it is the action of simultaneous bond formation and cleavage between the two fragments.

DOI:10042/to-2883

c)

A further optimisation was carried out on the chair TS however this time the bond lengths between the two fragments was set to 2.2A. This method alows the restof the molecule ti be optimised to a minimum however keeps the crucial TS bonds the same length.

DOI:10042/to-2884

d)

The bonds were then unfrozen and further optimised however this time using a TS optimisation. The structures and geometries were then examined and compared.

Bond Length Comparison
Bond	Structure b)	Structure d)
1-9	2.020	2.200
3-11	2.020	2.199
1-2	1.389	1.381
2-3	1.389	1.381
9-10	1.389	1.381
10-11	1.389	1.381

Bond Angle Comparison
Bond	Structure b)	Structure d)
9-10-11	120.487	121.958
1-2-3	120.491	121.958
2-3-11	101.853	99.653
10-11-3	101.850	99.642
2-1-9	101.846	99.626
1-9-10	101.860	99.634

The tables show that despite the 2 structures being very similar visually, every bond angle and length has changed to some degree.

DOI:10042/to-2885

e)

Now the boat transition structure is to be optimised, this however is not quite as straight forward as the chair TS. The QST2 method of calculation will be used. The anti2 structure from the first exercise is imported. Using the QST2 method means that the product and reactant must be labelled correctly. The link between C 3 and 4 breaks and a new bond forms between C 1 and 6.

The calculation can now be run however it will fail. This is because the products and reactants are too far away from the TS for Gaussian to recognise it. The structure must therefore be manipulated to one which is close to the transition structure. The calculation can now be run to give a good result of the TS.

DOI:10042/to-2886

f) Boat TS

The next step is to employ the Intrinisic Reaction Coordinate or IRC method, this is a way of working back from the transition state to see the geometry of the starting material.

This calculation was run originally over 50 steps to give the following structure.

The graph indicates that the molecule has not reached an energy minimum but the energy is still decreasing, the energy would be at a minimum if the graph leveled out into a horizontal line. More steps are clearly needed to reach this minimum.

Total Energy -231.56977832 a.u.

DOI:10042/to-2887

i)

Here the last step was taken (51) and the molecule minimized from this point.

Total Energy -231.69266120 a.u.

DOI:10042/to-2888

A significant energy drop can be seen from the last conformation.

ii)

In this calculation 200 steps were used compared to the previous 50. The final result is much closer but still not quite at the minimum, you can tell this for a number of reasons, the total energy is still slightly higher than a straight forward optimisation above, the graph shows that the energy has almost leveled out however still not quite totally and also the structure looks quite highly strained.

Total Energy -231.68762782 a.u.

DOI:10042/to-2889

iii)

Total Energy -231.56979638 a.u.

DOI:10042/to-2890

At only 50 steps computing the force constants at every step makes little difference to the minimum energy as it is only useful at overcoming local minima.

If however more steps are used then the method bacomes alot more accurate. Here the force constants were calculated at every step on a calculation run using 300 steps. Calculation of the force constants help give a more accurate structure by reducing the chances of the molecule getting stuck in a local minima rather than the true optimisation.

Total Energy -231.69265689 a.u.

DOI:10042/to-2889

This corresponds to the Gauche 3 conformation calculated earlier. Despite this method being much more accurate than previous one it is still not as low in energy as the first method of optimisation. This is likely to be because we have calculated the product of the reaction rather than the reactant.

Total Energy Comparrison
Method	Energy/Hartree	Diffenence/Harteee	Diffenence/kJmol^-1
IRC 50 Steps	-231.569778	0.122883	600.79321
Minimisaton	-231.692661	0	0
IRC 200 Steps	-231.68762782	0.005034	13.21677
Force constant 50	-231.56979638	0.122865	322.58208
Force constant 200	-231.69265689	0.000004	0.01050

This shows that the minimisation is the lowest of the energies, this works for his case but may not work for more complex molecules or if the starting structure was not as close to the final structure.

g)

The activation energies were calculated by running further optimisations of the boat and chair transition states under the stricted basis set of B3LYP/6-31G*.

Here is a comarison of both molecules under both basis sets.

Chair
	HF/3-21G	B3LYP/6-31G*
Energy(a.u.)	-231.615	-234.557
Energy Difference (kJmol^-1)	0	-7724.176
TS Vibration	-818.25	-565.46
C1-C2-C3/C4-C5-C6 Bond Angle	121.958	119.958
DistDistance between fragments(Å)	2.200	1.967

Boat
	HF/3-21G	B3LYP/6-31G*
Energy(a.u.)	-231.603	-234.543
Energy Difference (kJmol^-1)	0	-7719.731
TS Vibration	-839.725	-530.58
C1-C2-C3/C4-C5-C6 Bond Angle	121.693	122.268
DistDistance between fragments(Å)	2.140	2.206

The table shows that there is little difference in geometries howver there if a fairly major difference in the energies. There is a particularly large difference in the frequancies of transition states. from this evidence it is fair to say that a looses optimisation is good for predicting the geometry of a transition state but a stricter basis set should be used for predicting energies.

Optimisation of the Gauche 3 structure was run using the B3LYP/6-31G* basis set in order to calculate the totatal energy. The difference between this energy and the total energy of the boat and char TS gives the activation energy.

Activation energy
	Gauche 3	Chair	Boat
Total Energy(a.u.)	-234.611	-234.557	-234.543
Total Energy / kJmol^-1	-615971.227	-615829.45	-615792.693
Energy Difference (Activation energy) / kJmol^-1	0	141.777	178.534

This shows that the chair structure has the lowest activation energy so is the most acessable TS and hence kenetically favoured.

Diels Alder

The Diels Alder reaction is a pericyclic cycloaddition reaction which occours between an alkene and a 1,3-diene. The reaction is a concerted reaction. The pi orbitals of the dieneophile form a new sigma bonds to the diene. bellow is a general cycloaddition reaction scheme.

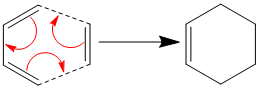
i)

Cis butadiene was drawn in gausview and the structure optimised using the AM1 semi-empirical molecular orbital method. Once optimised the HOMO and LUMO molecular orbitals were plotted.

The HOMO is antisymetric with respects to the plane (the plane running vertically down between the two central carbon atoms). the LUMO however is symetric with respects to the plane.

The same was also done for ethene.

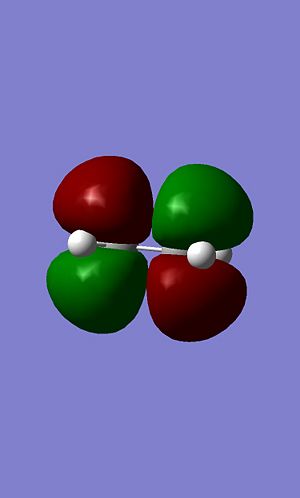In this case HOMO is symetric with respects to the plane whereas LUMO is antisymetric with respects to the plane.

The symetric LUMO of the diene is then able to overlap with the HOMO of the ethene allowing a reaction.

ii)

The single imaginary frequency of -818.27 cm^-1 confirm that the cis butadiene and ethene are in a Diels Alder transition state. This frequency also indicates the action of bond formation.

The HOMO and LUMO of the Diels-Alder were also calculated.

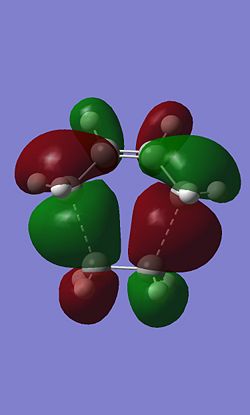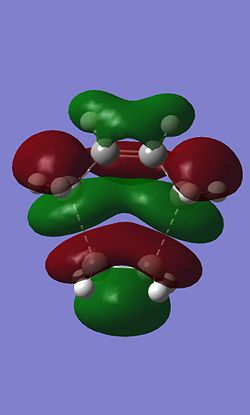In this case the HOMO is antisymetric and the LUMO is symetric. On the HOMO the there are nodes on each of the carbon atoms.

iii)

When the dienophile is more complex than ethene the regioselectivity of the product and TS becomes an important issue that needs to be concidered. Diels alder tend to have a high selectivity towards the endo product^[1] under kenetic conditions. This is due to good orbital overlap between the diene and dienophile orbitals.


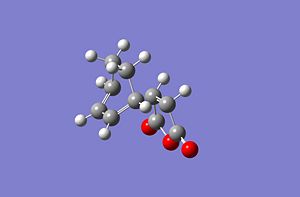	Exo	Endo
Energy (a.u.)	0.04044577	0.00916161
Energy difference kJmol^-1	0	82.136568337
Imaginary Vibration cm^-1	-480.33	-298.08
New C-C bond length A	2.179	2.117

This shows that the exo TS is higher in energy than the endo TS.

This difference in energy may be better understood by examening the HOMO and LUMO's of the transition states.

Exo MO's

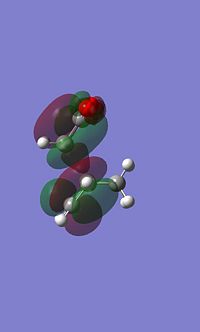It is apparent that these atomic orbitals are not quite symetrical, this is likely due to an error in the calculation, despite this they still depict the key areas of electron density.

Endo MO's

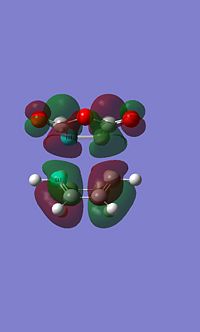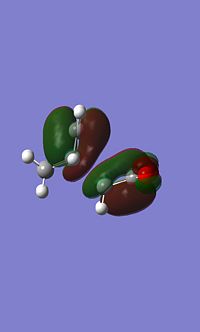You can see signs of secondary orbital overlap in the side HOMO of the endo TS above, the main bonding orbital where the new bonds are forming have a secondary lobe from the C=C bonds, even though this lobe is small electron density will have been donated from this into the main bonding lobe increasing the stabilisation. The overlap is occuring between the pi orbitals on the C=C bond and the pi* orbitals of the carbonyl.

The diagram below may help explain this.^[2]

It is this type of interaction occuring between the pi orbitals on the C=C bond and the pi* orbitals of the carbonyl which stabilises the endo TS. This is not possible in the exo product as the fragments are not in the correct orientation for an interaction to occour.

References

[1] ttp://www.ch.ic.ac.uk/motm/porphyrins/introDA.html

[2] ttp://pubs.acs.org/doi/pdf/10.1021/jo00384a016

[1]

[2]