Jump to content

Rep:Mod:TF910

From ChemWiki

Module 2

Introduction

The aim of this course is to give a preview into the chemical structure and bonding present in molecules. Gaussview 5.0.9 linked to the Gaussian software was used to carry out calculations.

The first week consists of understanding the Gaussview 5.0.9 software and learning how to carry out calculations including optimisation, frequency and MO analysis of various molecules which include BH3, TlBr3 and BBr3. Kinetic and thermodynamic properties of the molecule can then able to be determined.

When a molecule is optimised on Gaussian the nuclei are assumed to be in fixed positions relative to the electrons - this allows the Schrödinger equation to be solved for the nuclei position - this corresponds to the OPT part of the calculation and the optimised molecule is the one with the lowest energy geometry.

Molecule Optimisation

BH3 - B3LYP, 3-21G optimisation

Initially, a minimal basis set (3-21G) was chosen along with a DFT method and B3LYP hybrid functional

File:BH3 OPTIMISATION Faber.LOG


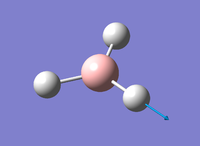
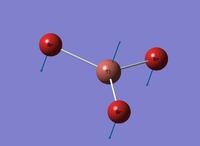
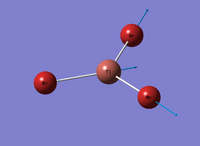
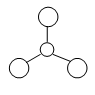
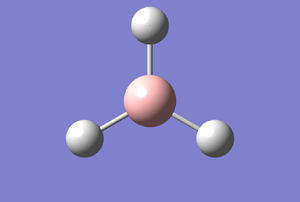Figure 1: Gaussview Image of optimised BH3


Bond angle: 120°

H-B-H bond distance: 1.19 Å


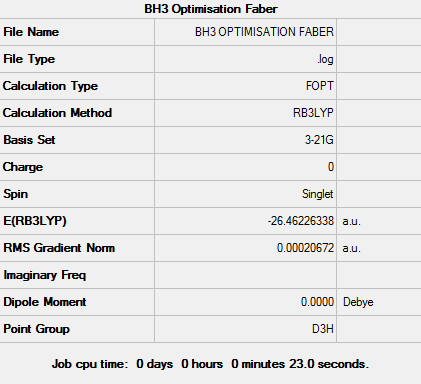Figure 2: Summary of optimised BH3 


     Item                  Value     Threshold  Converged?
Maximum Force            0.000090     0.000450     YES
RMS     Force            0.000059     0.000300     YES
Maximum Displacement     0.000352     0.001800     YES
RMS     Displacement     0.000230     0.001200     YES

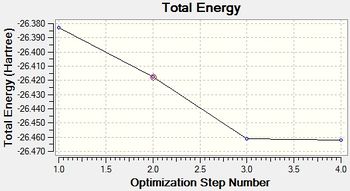
The data indicates that the optimisation has been completed successfully this is further backed up by the fact that the RMS Gradient Normal is less than 0.001.

The first graph above has given the energy of the molecule at each step of the optimisation. The second shows the gradient of the energy of the BH3 molecule at each step of the optimisation.

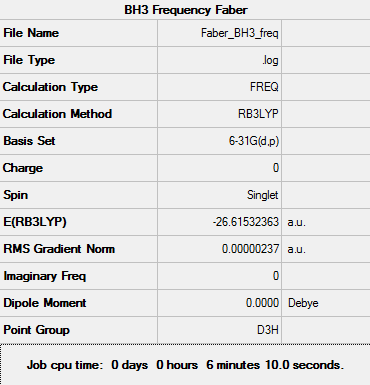
BH3 - B3LYP, 6-31G d,p optimisation

Next a higher level 6-31G(d,p) basis set was used in conjunction with the DFT method and B3LYP hybrid function which was used initially.

File:BH3 OPTIMISATION 6-31G FABER.LOG

Figure 3: Summary of optimised BH3 using 6-31G minimal basis set 

      Item                 Value     Threshold  Converged?
Maximum Force            0.000005     0.000450     YES
RMS     Force            0.000003     0.000300     YES
Maximum Displacement     0.000019     0.001800     YES
RMS     Displacement     0.000012     0.001200     YES

Data indicates that the optimisation has been completed as the value for RMS Gradient Norm is less than 0.001.


Total energy comparison between the minimal basis sets

Total energy for the 3-21G optimised structure = -26.46226338 a.u.

Total energy for the 6-31G(d,p) optimised structure = -26.61532363 a.u.


Bond angle: 120°

H-B-H bond distance: 1.19 Å

TlBr3 - optimisations using pseudo-potentials

The optimisation was run with the addition of a point group restriction on the TlBr3 atom (D3h, 0.001 - very tight) and the basis set LanL2DZ was used with B3LYP hybrid. It was submitted to the HPC server.


The log file for the the TlBr3 optimisation can be seen below:

File:TLBR3 OPTIMISATION FABER.LOG

D-Space - http://hdl.handle.net/10042/23409


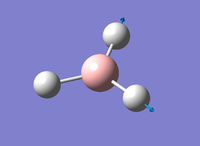
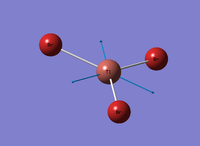
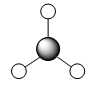
Figure 4: A Gaussview image of optimised TiBr3


Bond angle: 120°

Br-Tl-Br bond length: 2.65 Å 



        Item               Value     Threshold  Converged?
Maximum Force            0.000002     0.000450     YES
RMS     Force            0.000001     0.000300     YES
Maximum Displacement     0.000022     0.001800     YES
RMS     Displacement     0.000014     0.001200     YES


The calculated Tl-Br bond length after optimisation is 2.65 Å which compares to the literature for the experimentally obtained value of 2.52 Å [2]. Though there is a fairly good comparison betweeen the two values, the slight discrepancy could have been minimised by using a better basis set. On the whole, however, it is important to get the correct balance between a better optimisation and a more time consuming calculation.

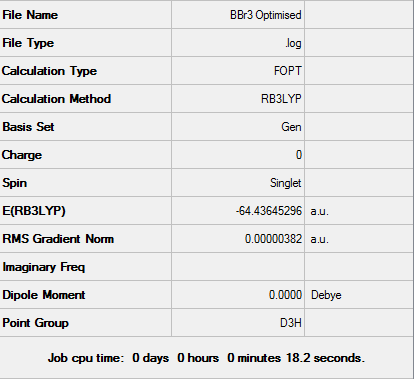
BBr3 Optimisation using a mixture of basis sets and pseudo potentials

In this calculation both a 6-31G (d,p) basis set, together with a LanL2DZ basis set (B3LYP hybrid functional as before) was employed. The use of both basis sets is to take into account the imbalancein the B-Br bond.

The log file for the BBr3 optimisation can be seen below:

File:BBr3 Optimised log file.txt

D-space - http://hdl.handle.net/10042/23372

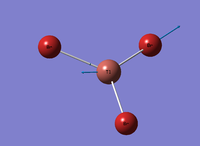
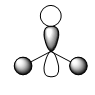
Figure 5: A Gaussview image of optimised BBr3


Bond angle: 120°

Br-B-Br bond length: 1.93 Å 




        Item               Value     Threshold  Converged?
Maximum Force            0.000008     0.000450     YES
RMS     Force            0.000005     0.000300     YES
Maximum Displacement     0.000036     0.001800     YES
RMS     Displacement     0.000023     0.001200     YES

The definition of a bond

Gaussview occasionally will not display bonds in structures where one would normally expect to see one. This is due to the fact that Gaussview principally uses bond lengths in organic molecules. For this reason a bond is not drawn when a calculated bond length is longer than usually would be expected - it is distance dependent.

In reality, bonds can be seen as a given interaction in an area of high electron density between two atoms. In an ionic bond the interaction can be defined as an electrostatic force of attraction between oppositely charged ions. Conversely, a covalent bond involves the attraction of molecular orbitals which have suitable symmetry. Practically speaking the true nature of a bond is found, on the whole, in between covalent and ionic with regards to bond character. A bond's strength increases as the two atoms approach each other from an infinite distance, and is not, as can be seen in Gaussview structures, formed at a set distance.


Comparison of bond lengths in BH3, TlBr3 and BBr3

Bond Optimised Bond length (Å) Experimental Bond length (Å) Basis set
B-H 1.19 1.19 [1] 6-31G(d,p)
Tl-Br 2.65 2.52 [2] LanL2DZ
B-Br 1.93 1.88 [3] GEN

If you look at the variations in bond length between the molecules, conclusions can be made as to the role that different ligands as well as different periodicity of the central atom has on the strength of the bond.

In the case of comparing the BH3 and BBr3 molecules the effect of replacing the hydrogen atoms with bromine atoms is that the bond length is considerably increased (from 1.19 Å in BH3 to 1.93 Å in BBr3). Clearly the principal difference between to two ligands is their relative size. Bromine in considerably larger than hydrogen. Being much larger the bromine atom has a diffuse outer electron shell which restricts the efficiency of its electronic interaction with the central boron atom. When considering hydrogen, however, its size is similar to that of the boron atom meaning they can interact more strongly. Another factor which can be considered when comparing the bond lengths is the effect of electronegativity. Bromine is more electronegative than hydrogen meaning that the B-Br bond is more polar than B-H thus distortion of the shared electrons occurs lengthening the bond.

When looking at the differences in the bond length between TlBr3 and BBr3 the Tl-Br bond (2.65 Å) is much longer than the B-Br bond (1.93 Å). Both the thallium and boron are in the same group but thallium lies 4 periods below boron. Since it is a lot larger, thallium has a much poorer overlap with the bromine atoms as its 6p outer shell electrons are more diffuse than those of boron whose outer shell electrons are contained in a 2p orbital much closer to the nucleus. This results in a shorter B-Br bond than Tl-Br.

Frequency Analysis

BH3 vibrational analysis

Vibrational analysis was performed using the BH3 structure which had already optimised (DFT, B3LYP, 6-31G (d,p)).

The log file can be seen here: File:FABER BH3 FREQ.LOG 


       Item               Value     Threshold  Converged?
Maximum Force            0.000005     0.000450     YES
RMS     Force            0.000002     0.000300     YES
Maximum Displacement     0.000019     0.001800     YES
RMS     Displacement     0.000009     0.001200     YES


Frequency values have been taken from the log output file: 

Low frequencies ---   -0.9033   -0.7343   -0.0054    6.7375   12.2491   12.2824
Low frequencies --- 1163.0003 1213.1853 1213.1880

The IR spectrum produced from Gaussview for BH3 can be seen below:

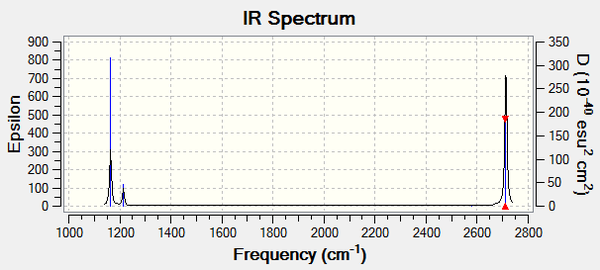Figure ****: The IR Spectrum of BH3


A description of the BH3 vibrations along with their corresponding Gaussview images can be seen in the table below:

Number Vibrational Mode Frequency (cm-1) Intensity (cm-1) Symmetry Point Group Description of vibration
1 1163 93 A2 All the hydrogen atoms move up and down the plane of the principal axis in a concerted manner. The boron atom moves along the same plane of the principal axis but in the opposite direction. This leads to a considerable dipole moment.
2 1213 14 E' Two of the hydrogens bend towards eachother in the plane which is perpendicular to the principal axis. The third hydrogen remains stationary.
3 1213 14 E' Asymmetric rocking action of all three of the hydrogen atoms in the plane of the molecule.
4 2582 0 A'1 All the hydrogen atoms move in and out of the plane in a concerted manner while the boron atom remains stationary.
5 2715 126 E' Asymmetric stretching of two B-H bonds in opposite directions the other B-H bond stretches only slightly.
6 2715 126 E' Two hydrogens stretch symmetrically in phase - they lengthen and shorten equally. While they lengthen the third hydrogen shortens and vice versa.


Generally the number of vibrational modes is given by 3N-6 where N is the number of atoms in a molecule. So for BH3 with N=4 there are 6 modes expected. In the spectrum there are only 3 clear peaks although there are 6 vibrational modes. In order for a peak to be visible on an IR spectrum the molecule must have a change in dipole moment. Initially it is clear that because the A'1 stretch is completely symmetric with all the hydrogens moving in and out of the plane in a concerted manner, this stretch is IR inactive. In the A2 vibration there is a clear change in dipole moment and so this vibration is IR active. Of the last 4 vibrations, there are two sets of degenerate pairs and so only 2 peaks are seen contrary to the 4 one would expect. The three vibrations which lead to the peaks in the spectrum are the A'2' (1163 cm-1), E' (1213 cm-1), E' (2715 cm-1).

TlBr3 vibrational analysis

Vibrational analysis was performed using the TlBr3 structure which had already optimised (DFT, B3LYP, 6-31G (d,p)).

The log file can be seen here: File:FABER TLBR3 FREQ.txt

D-space - http://hdl.handle.net/10042/23409 



        Item               Value     Threshold  Converged?
Maximum Force            0.000002     0.000450     YES
RMS     Force            0.000001     0.000300     YES
Maximum Displacement     0.000022     0.001800     YES
RMS     Displacement     0.000011     0.001200     YES


Frequency values have been taken from the log output file: 

Low frequencies ---   -3.4213   -0.0026   -0.0004    0.0015    3.9367    3.9367
Low frequencies ---   46.4289   46.4292   52.1449


The IR spectrum produced from Gaussview for TlBr3 can be seen below:

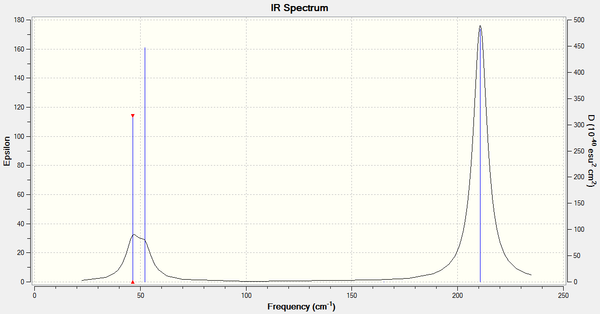Figure 6: The IR Spectrum of TlBr3


A description of the TlBr3 vibrations along with their corresponding Gaussview images can be seen in the table below:

Number Vibrational Mode Frequency (cm-1) Intensity (cm-1) Symmetry Point Group Description of vibration
1 46 3.7 E' One of the bromine atoms remains stationary with respect to the Tl atom. The remaining two bromine atoms bend towards each other in the plane perpendicular to the principal axis.
2 46 3.7 E' Asymmetric rocking action of all three of the bromine atoms in the plane of the molecule - 2 in one direction and one in the other.
3 52 5.8 A2 All the bromine atoms move up and down the plane of the principal axis in a concerted manner. The thallium atom moves along the same plane of the principal axis but in the opposite direction. This leads to a considerable dipole moment.
4 165 0 A'1 Symmetric stretching of all three of the Tl-Br bonds in the plane of the molecule
5 211 25 E' Two bromines stretch symmetrically in phase - they lengthen and shorten equally. While they lengthen the third bromine shortens and vice versa.
6 211 25 E' Two of the Tl-Br stretch symmetrically bonds in a concerted manner, while the other Tl-Br bond stretches out of phase which leads to asymmetry.


As in the case of BH3, there are also three peaks in the infrared spectrum of TlBr3. One peak is at 46 cm-1 which is the lowest "real" normal mode. This corresponds to the degenerate vibrational modes of 1 and 2. The peak at 52 cm-1 is from vibrational mode 3 and the peak at 211 cm-1 again from a set of degenerate vibrations 5 and 6. Vibration 4 is totally symmetrical and hence is IR inactive.

Comparison of BH3 and TlBr3 Vibrational Frequencies

A table of the vibrational frequencies of BH3 and TlBr3 can be seen below:

BH3 frequency (cm-1) TlBr3 frequency (cm-1)
1163 46
1213 46
1213 52
2582 165
2715 211
2715 211


When comparing the two molecules, the obvious thing to recognize is that the frequency values of BH3 are much larger than those of TlBr3. The reason for this is that the bond vibration frequency corresponds to the bond strength. For reasons mentioned earlier the B-H bond can be shown to be stronger than the Tl-Br bond. Another approach which can explain the lower frequencies present in TlBr3 is Hooke's Law. This inversely relates vibrational frequency with the reduced mass of the molecule. Since TlBr3 is much heavier it has a higher reduced mass and hence a lower vibrational frquency in comparison to BH3.

The vibrational modes order seen in the two molecules also differs slightly. In BH3 the modes are arranged in the order - A2’, E', E', A1', E', E' whereas for TlBr3 the order is E',E', A2’, A1' E', E'. A clear similarity is that both show 6 vibrational modes which is to be expected as the two molecules both have the same structure. Another interesting comparison is in the two IR spectra which both exhibit three peaks.

For both spectra two pairs of modes lie fairly close together, the A2 and E' modes and also the A1' and E' modes which are energetically higher. This could perhaps be explained by vibronic coupling between vibration modes in both molecules. In order for this to have a significant effect the two coupling vibration modes should share a bond or atom - this is clearly possible in the trigonal planar arrangement.

Throughout the calculations, the same method and basis set for both the optimisation and the frequency analysis was used. This is to ensure that comparisons can be made betweeen the two molecules. By using a different basis set and or method any comparisons made are not valid.

The main purpose of carrying out a frequency analysis is to verify that the structure which has been optimised is at a minimum. It can also be very useful to provide information such as the frequency of vibration and helps in the analysis of vibrational modes and the interpretation of IR spectra in comparable molecules.

The low frequencies represent the "-6" part in the equation for the number of vibrational modes: "3N-6". They are representative of the motions of the centre of mass of the molecule.

Population Analysis

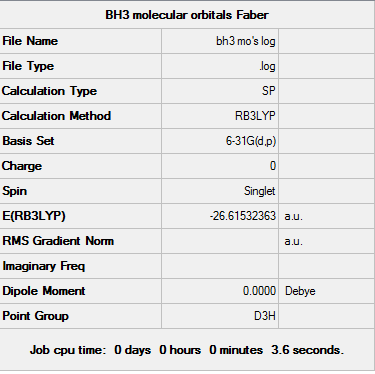
BH3 Molecular Orbitals

A further energy calculation was run using a previously optimised BH3 structure (DFT, B3LYP, 6-31G (d,p)).

The log file can be seen here: File:Bh3 mo's log.log

D-space - http://hdl.handle.net/10042/23439

The MO diagram constructed using the LCAO method is shown below:


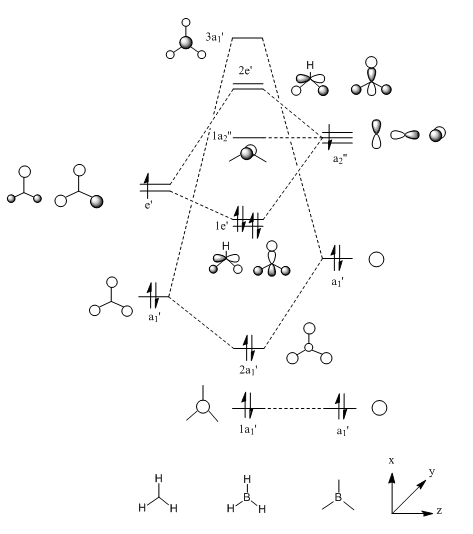
The following table shows the comparison between the LCAO orbitals and the real Gaussview produced molecular orbitals:

Method 1 2 3 4 5 6 7 8
LCAO
Real (Gaussview)
Symmetry Label a1' a1' e' e' a2 a1' e' e'

By comparing the two different sets of molecular orbitals, it is clear to see there is a very close match between the LCAO constructed MOs and the Gaussview calculated MOs. This proves the the Linear Combination of Atomic Orbitals is a valid approach for accurate construction of MOs in relatively small and uncomplicated molecules such as BH3.

NBO Analysis

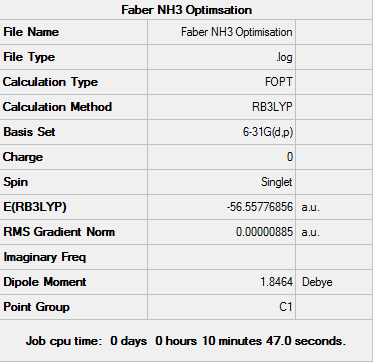
NH3 Optimisation Practice

The optimisation of NH3 was carried out in Gaussview using the RB3LYP calculation method and a 6-31G basis set. The "nosymm" keyword was applied.

The log file can be seen here: File:FABER NH3 OPTIMISATION.LOG 



        Item               Value     Threshold  Converged?
Maximum Force            0.000024     0.000450     YES
RMS     Force            0.000012     0.000300     YES
Maximum Displacement     0.000079     0.001800     YES
RMS     Displacement     0.000053     0.001200     YES


Frequency Analysis

A further frequency analysis for NH3 was performed using the previously optimised structure (DFT, B3LYP, 6-31G (d,p)).

The log file can be seen here: File:FABER NH3 FREQUENCY.LOG 

        Item               Value     Threshold  Converged?
Maximum Force            0.000022     0.000450     YES
RMS     Force            0.000009     0.000300     YES
Maximum Displacement     0.000078     0.001800     YES
RMS     Displacement     0.000039     0.001200     YES

Low frequencies ---  -30.7927   -0.0019   -0.0018   -0.0014   20.2690   28.2324
Low frequencies --- 1089.5544 1694.1237 1694.1863


Population Analysis

An energy calculation was executed using the previously optimised NH3 structure (DFT, B3LYP, 6-31G (d,p)).

The log file can be seen here: File:FABER NH3 POPANALYSIS.LOG


NBO Analysis of NH3

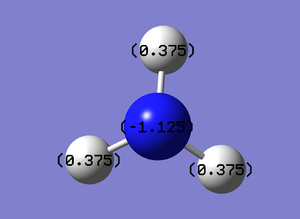
NBO visualisation on Gaussview:

The charge range is between -1.125 and 1.125:


The NBO charges were then shown using Gaussview:

Nitrogen NBO charge: -1.125 Hydrogen NBO charge: +0.375


NH3BH3 Analysis

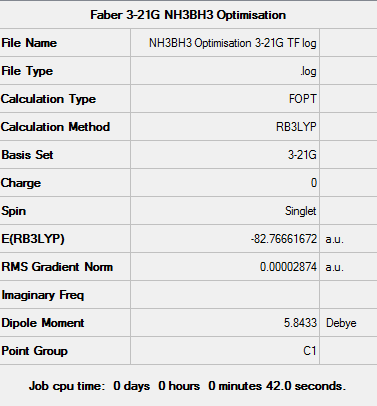
Optimisation using 3-21G basis set

Firstly, the 3-21G minimal basis set was chosen along with a DFT method and B3LYP hybrid functional.

The log file can be seen here: File:NH3BH3 Optimisation 3-21G TF log.txt

D-space - http://hdl.handle.net/10042/23470 


        Item               Value     Threshold  Converged?
Maximum Force            0.000082     0.000450     YES
RMS     Force            0.000030     0.000300     YES
Maximum Displacement     0.000585     0.001800     YES
RMS     Displacement     0.000204     0.001200     YES


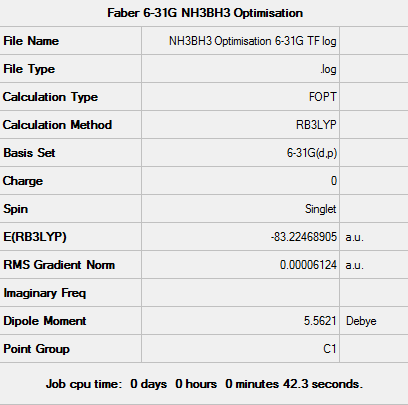
Optimisation using 6-31G(d,p) basis set

Following the initial optimisation a higher level basis set (6-31G, (d,p)) was chosen along with a DFT method and B3LYP hybrid functional.

The log file can be seen here: File:NH3BH3 Optimisation 6-31G TF log.txt

D-space - http://hdl.handle.net/10042/23474 

        Item               Value     Threshold  Converged?
Maximum Force            0.000137     0.000450     YES
RMS     Force            0.000039     0.000300     YES
Maximum Displacement     0.000999     0.001800     YES
RMS     Displacement     0.000216     0.001200     YES


Frequency Analysis

A frequency analysis was done using the NH3BH3 structure which had been previously optimised. (DFT, B3LYP, 6-31G (d,p)).

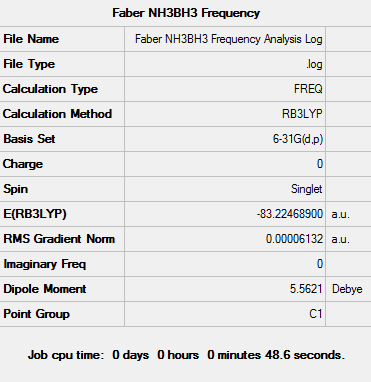
The log file can be seen here: File:Faber NH3BH3 Frequency Analysis Log.txt

D-space - http://hdl.handle.net/10042/23475 

        Item               Value     Threshold  Converged?
Maximum Force            0.000276     0.000450     YES
RMS     Force            0.000061     0.000300     YES
Maximum Displacement     0.001504     0.001800     YES
RMS     Displacement     0.000378     0.001200     YES



Low frequencies ---  -18.4028   -0.0012   -0.0009   -0.0006   12.2831   16.7843
Low frequencies ---  262.4600  631.2099  637.6447

Determination of the dissociation energy

The energies calculated from the three optimised structures can be seen below:

E(BH3)= -26.61532363 a.u.

E(NH3)= -56.55776856 a.u.

E(NH3BH3)= -83.22468905 a.u.


ΔE = E(NH3BH3) - [E(NH3)+ E(BH3)]

ΔE = -83.22468905 - (-56.55776856 + (-26.61532363)]

ΔE = -0.05159686 a.u.


Energy of dissociation = -135.4 kJ/mol


Week 2 - Lewis Acids and Bases

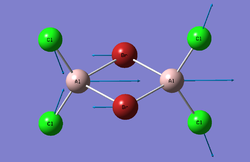
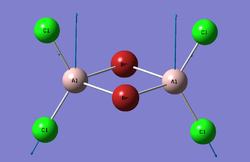
Cl2Al(μ-Br2)AlCl2

Optimisation

The log file can be seen here: File:Al2Br2Cl4 6-31G GEN Optimisation TF log.txt

D-space - http://hdl.handle.net/10042/23558



Calculation summary
Parameters
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set GEN
Charge 0
Spin Singlet
Total energy(a.u.) -2352.40630798
RMS Gradient(a.u.) 0.00000396
Dipole Moment(Debye) 0.0000
Point Group D2h
Time taken 3 minutes 22.1 seconds 
        Item               Value     Threshold  Converged?
Maximum Force            0.000007     0.000450     YES
RMS     Force            0.000003     0.000300     YES
Maximum Displacement     0.000170     0.001800     YES
RMS     Displacement     0.000059     0.001200     YES

Frequency Analysis

The log file can be seen here: File:Al2Br2Cl4 6-31G GEN FREQ TF log.txt

D-space - http://hdl.handle.net/10042/23785 

Low frequencies ---   -5.1798   -5.0280   -3.2282   -0.0033   -0.0026   -0.0014
Low frequencies ---   14.8293   63.2820   86.0840

        Item               Value     Threshold  Converged?
Maximum Force            0.000013     0.000450     YES
RMS     Force            0.000004     0.000300     YES
Maximum Displacement     0.000231     0.001800     YES
RMS     Displacement     0.000100     0.001200     YES

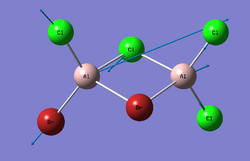
Cis-BrClAl(μ-Cl2)AlClBr

Optimisation

The log file can be seen here: File:Al2Br2Cl4 Isomer 2 6-31G GEN Optimisation TF log.log

D-space - http://hdl.handle.net/10042/23668


Calculation summary
Parameters
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set GEN
Charge 0
Spin Singlet
Total energy(a.u.) -2352.41626677
RMS Gradient(a.u.) 0.00001470
Dipole Moment(Debye) 0.1658
Point Group C2v
Time taken 4 minutes 13.2 seconds 


        Item               Value     Threshold  Converged?
Maximum Force            0.000040     0.000450     YES
RMS     Force            0.000016     0.000300     YES
Maximum Displacement     0.001360     0.001800     YES
RMS     Displacement     0.000424     0.001200     YES

Frequency Analysis

The log file can be seen here: File:Al2Br2Cl4 Isomer 2 6-31G GEN FREQ TF log.txt

D-space - http://hdl.handle.net/10042/23797 

Low frequencies ---   -3.8194   -2.2357   -0.0040   -0.0032   -0.0027    1.3863
Low frequencies ---   17.2011   50.9456   78.5393

        Item               Value     Threshold  Converged?
Maximum Force            0.000048     0.000450     YES
RMS     Force            0.000015     0.000300     YES
Maximum Displacement     0.001466     0.001800     YES
RMS     Displacement     0.000541     0.001200     YES

Trans-BrClAl(μ-Cl2)AlClBr

Optimisation

The log file can be seen here: File:Al2Br2Cl4 Isomer 3 6-31G GEN Optimisation TF loog.txt

D-space - http://hdl.handle.net/10042/23815


Calculation summary
Parameters
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set GEN
Charge 0
Spin Singlet
Total energy(a.u.) -2352.41629858
RMS Gradient(a.u.) 0.00001563
Dipole Moment(Debye) 0.0000
Point Group C2h
Time taken 4 minutes 11.3 seconds 
        Item               Value     Threshold  Converged?
Maximum Force            0.000039     0.000450     YES
RMS     Force            0.000015     0.000300     YES
Maximum Displacement     0.000464     0.001800     YES
RMS     Displacement     0.000166     0.001200     YES

Frequency Analysis

The log file can be found here: File:Al2Br2Cl4 Isomer 3 6-31G GEN FREQ TF log.txt

D-Space - http://hdl.handle.net/10042/23821 

Low frequencies ---   -4.8002   -0.0033   -0.0032   -0.0014    1.4545    2.2600
Low frequencies ---   18.1746   49.1207   73.0075

        Item               Value     Threshold  Converged?
Maximum Force            0.000050     0.000450     YES
RMS     Force            0.000016     0.000300     YES
Maximum Displacement     0.000572     0.001800     YES
RMS     Displacement     0.000254     0.001200     YES

BrClAl(μ-Br,Cl)AlCl2

Optimisation

File:Al2Br2Cl4 Isomer 4 6-31G GEN Optimisation TF log.txt

D-space - http://hdl.handle.net/10042/23768


Calculation summary
Parameters
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set GEN
Charge 0
Spin Singlet
Total energy(a.u.) -2352.41109944
RMS Gradient(a.u.) 0.00001563
Dipole Moment(Debye) 0.1385
Point Group C2
Time taken 4 minutes 6.4 seconds 
        Item               Value     Threshold  Converged?
Maximum Force            0.000035     0.000450     YES
RMS     Force            0.000014     0.000300     YES
Maximum Displacement     0.000524     0.001800     YES
RMS     Displacement     0.000183     0.001200     YES

Frequency Analysis

The log file can be seen here: File:Al2Br2Cl4 Isomer 4 6-31G GEN FREQ TF log.txt

D-space - http://hdl.handle.net/10042/23808 

Low frequencies ---   -2.2898   -0.0026   -0.0014    0.0010    1.2536    3.3243
Low frequencies ---   17.1617   55.9535   80.0563

        Item               Value     Threshold  Converged?
Maximum Force            0.000034     0.000450     YES
RMS     Force            0.000016     0.000300     YES
Maximum Displacement     0.001340     0.001800     YES
RMS     Displacement     0.000523     0.001200     YES


Infrared Spectroscopy

Cl2Al(μ-Br2)AlCl2

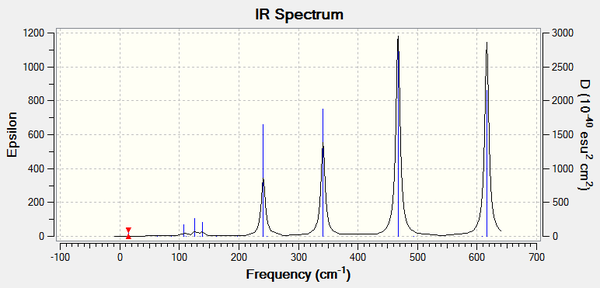
The IR spectrum for Cl2Al(μ-Br2)AlCl2 can be seen below:

Infrared Data
Number Frequency (cm-1) Intensity Vibration Mode Description
1 241 99.7 Asymmetric stretching of Al-Br bonds in plane of bridging atoms where also there is bouncing of Al-Cl bonds
2 341 161 Al atoms rock in the plane of Al-Br-Al-Br atoms
3 467 347 Al-Br antisymmetric stretch with a scissor-like motion of the Al-Cl bonds
4 616 332 Al-Br antisymmetric scissor-like motion peperndicular to plane of Al-Br-Al-Br. The Al-Cl bonds also move because of an asymmetric stretching mode

Cis-BrClAl(μ-Cl2)AlClBr

The IR spectrum for Cis-BrClAl(μ-Cl2)AlClBr can be seen below:

Infrared Data
Number Frequency (cm-1) Intensity Vibration Mode Description
1 419 411 Symmetric stretching of Al-μ Cl bonds, in plane of bridging atoms along the plane of symmetry, with Al atoms moving out of phase
2 461 34.5 Al atoms symmetric stretching both terminal and bridging bonds
3 582 278 Al atoms scissoring in phase with each other, parallel to the z-axis

Trans-BrClAl(μ-Cl2)AlClBr

The IR spectrum for Trans-BrClAl(μ-Cl2)AlClBr can be seen below:

Infrared Data
Number Frequency (cm-1) Intensity Vibration Mode Description
1 421 439 There is an asymmetric stretch of atoms in plane of bridging atoms, towards and away from Al atoms, with the two μ halide atoms moving out of phase with each other
2 579 316 There is an asymmetric stretch of the Al atoms, perpendicular to plane of bridging atoms where both of the Al atoms move in phase. The terminal halide bond lengths change sporadically and furthermore the angle to the bridging atoms also changes.

BrClAl(μ-Br,Cl)AlCl2

The IR spectrum for BrClAl(μ-Br,Cl)AlCl2 can be seen below:

Infrared Data
Number Frequency (cm-1) Intensity Vibration Mode Description
1 289 48.3 There is symmetric stretching of μ-Cl-Al bond, scissoring of terminal Cl-Al-Cl bonds
2 384 153 There is asymmetric stretching of Al-μ-halide bonds, terminal halides remain stationary
3 424 274 There is a symmetric stretch of terminal Cl-Al-Br bonds accompanied with a small symmetric stretch of the terminal Cl-Al-Cl bond
4 493 107 There is a symmetric stretch of terminal Cl-Al-Cl bonds accompanied with a small symmetric stretch of the terminal Cl-Al-Br bonds
5 574 122 There is out of plane motion up and down of the Al atom with attached Br and Cl terminal atoms. The remaining atoms stay motionless.
6 614 197 There is out of plane motion up and down of the Al atoms attached to two terminal Cl atoms. The remaining atoms stay motionless.

IR Analysis

The pre-requisite for a vibrational mode to be infrared active is that there must be a change in dipole moment associated with the molecule.

With the 4 isomers observed for Al2Br2Cl4 there are clearly 4 different spectra. The principle reason for the differences in the 4 spectra is the relative positions of the chlorine and bromine atoms. The position of these atoms is vital because it directly affects the molecular vibrations which in turn determines the nature of the dipole moment.

The large peaks which are clearly visible on the spectrum are caused by the various vibrational modes of each isomer which are infrared active (have a change in molecular dipole moment). Another factor which determines the number of peaks present in a spectrum is the symmetry of a molecule. The more symmetric a molecule is the fewer the number of peaks. These two factors can be best explained in the cis-BrClAl(μ-Cl2)AlClBr isomer and the trans-BrClAl(μ-Cl2)AlClBr isomer whose spectra are near identical.

When comparing the structure of the two molecules both have the two bridging chlorines so have fairly high symmetry - the only difference is the positions of the terminal bromine and chlorine. This leads to very similar stretches as illustrated by the two spectra. The peak at 461 cm-1 which is present in the -cis isomer does not appear in the -trans and this can be explained by the two different vibrations caused by slightly differing molecule symmetry. The -cis isomer vibrational mode at 461 cm-1 does appear because it results in a dipole moment change whereas this is not the case for the -trans equivalent.

If one compares the -cis and -trans to the other two isomers there are fewer intense peaks and this can also be explained by the highly symmetric nature of the former.

Relative Energies

The energies of the four optimised molecules can be seen in the table below:


Energy Comparison
Molecule Energy (a.u.) Energy (kJ/mol) Relative Energy (kJ/mol)
Cl2Al(μ-Br2)AlCl2 -2352.40630798 -6176242.762 26.23
Cis-BrClAl(μ-Cl2)AlClBr -2352.41626677 -6176268.908 0.08
Trans-BrClAl(μ-Cl2)AlClBr -2352.41629858 -6176268.992 0.00
BrClAl(μ-Br,Cl)AlCl2 -2352.41109944 -6176255.342 13.65

By comparing the energies, it is possible to determine the most stable of the isomers. In this case, Trans-BrClAl(μ-Cl2)AlClBr has the most negative value for energy (the lowest) and is therefore the most stable (having verified that all of the isomers have been fully optimised).

Trans-BrClAl(μ-Cl2)AlClBr which is the most stable isomer (from the respective energies) consists of two molecular fragments. In each of the two identical fragments there is an atom which can act as the electron pair acceptor (Lewis acid) and an atom which can act as the electron pair donor (Lewis base).

The relative stability of the trans isomer to the other three could be explained by these Lewis acid and Lewis base fragment pairs. The formation of the adduct complex is stabilised by the interaction betweeen the electron donating atom and the electron accepting atom which is not present in the other three isomers.


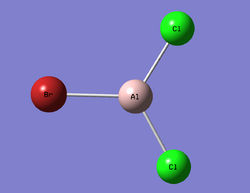
AlBrCl2 Optimisation

The log file can be seen here: File:AlBrCl2 Monomer 6-31G GEN Optimisation TF log.txt

D-Space - http://hdl.handle.net/10042/23853


Calculation summary
Parameters
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set GEN
Charge 0
Spin Singlet
Total energy(a.u.) -1176.19013697
RMS Gradient(a.u.) 0.00000291
Dipole Moment(Debye) 0.1134
Point Group C2h
Time taken 46.6 seconds 


        Item               Value     Threshold  Converged?
Maximum Force            0.000005     0.000450     YES
RMS     Force            0.000002     0.000300     YES
Maximum Displacement     0.000022     0.001800     YES
RMS     Displacement     0.000012     0.001200     YES

The energies calculated from the optimised monomer and adduct structures can be seen below:

E(monomer)= -1176.19013697 a.u. E(adduct)= -2352.41629858 a.u.

The Dissociation Energy can be calculated from the equation below:

ΔE = E(adduct) - [2 x E(monomer)]

Edissociation = -2352.41629858 - 2(-1176.19013697)

Edissociation = -0.03602464 a.u. = - 94.58 kJ/mol

The negative nature of this value is indicative of the fact that the adduct is favoured over the two dissociated monomers.

AlBrCl2 Frequency

The log file can be seen here: File:AlBrCl2 Monomer 6-31G GEN FREQ TF log.txt

D-space - http://hdl.handle.net/10042/23863

The low frequency values have been extracted from the corresponding output file and show that the frequency calculation is complete: 

Low frequencies ---   -2.4223    0.0010    0.0034    0.0038    2.7465    2.9629
Low frequencies ---  120.5194  133.8347  185.7791

        Item               Value     Threshold  Converged?
Maximum Force            0.000008     0.000450     YES
RMS     Force            0.000003     0.000300     YES
Maximum Displacement     0.000021     0.001800     YES
RMS     Displacement     0.000009     0.001200     YES


Molecular Orbitals

Molecular Orbital Orbital Number (With Energy (a.u.)) Comments
68 (-0.42931) This molecular orbital exhibits very strong bonding character which is stabilised by a very aromatic-like cloud of electron density. The main interactions involve in-phase p orbital overlap of the bridging Cl and the two Al atoms leading to strong bonding interactions. The MO is further stabilised by the p orbitals of the terminal halide atoms which are all correctly orientated to increase the overlap encouraging the mixing which feeds directly into the aromatic like system. Overall there are five nodal planes. One goes through the two bromine atoms. Another dissects the bridging chlorine atoms and the two aluminium atoms which are all in the same plane. The other nodal planes are perpendicular to the aforementioned one and bisect the termainal halides and aluminium bonds.
67 (-0.45914) The molecular orbital here exhibits strong bonding character with interactions along the aluminium atoms and the terminal chlorines. This is enhanced by strong interaction between the aluminium atoms and the bridging chlorine atoms. However, a slight destabilising effect is caused by weak through space antibonding interactions between the two aluminium atoms. Overall there are 6 nodal planes present in this molecular orbital. Four of them are perpendicular to the bonds between the aluminium and the terminal halides atoms. The other two nodal planes are present both above and below the planes of the terminal halide (parallel to each other).
65 (-0.50715) The molecular orbital demonstrates antibonding interactions between the aluminium atom and the terminal halide atoms. Less significant through space interactions are present between the the Al atoms and the bridging halides. There is a weakly bonding through space interactions between the terminal halide on a single aluminium atom as well a very weak through space antibonding interaction between the halide atoms attached to different aluminium atoms. Overall there are five nodal planes. One goes through the two bromine atoms. Another dissects the bridging chlorine atoms and the centre of inversion. The other nodal planes are perpendicular to the aforementioned one and bisect the termainal halides and aluminium bonds.
70 (-0.40817) The molecular orbital demonstrates an antibonding character as a whole. This antibonding character can be seen with a strong antibonding interaction between both of the chlorines in the bridging positions. The molecule also contains some non-bonding interactions highlighted by the fact that atoms in the molecule contain no electron density and therefore there are no orbital interactions - the bridging halogens is where the electron density lies. There are three nodal planes for this MO all parallel to eachother. One nodal plane lies in the plane of the two Al atoms and the other two intersect the two bridging chlorine atoms.
79 (-0.32163) There is strong antibonding character between the Br and Cl atoms. The number of nodal planes is 6. Each node occurs between the bond between the terminal halides. As Br is a bigger atom than Cl, it has larger, more diffuse orbitals. This point is demonstrated in the MOs, where the Br pz orbitals are larger than the Cl pz orbitals, with pi antibonding interactions between them.

References

[1] ↑ M. Schuurman, W. Allen, H. Schaefer, Journal of Computational Chemistry, 2005, 26, 1106

[2] ↑ J. Blixt et al., J. Am. Chem. Soc. , 117, 1995, pp 5089 - 5104

[3] ↑ C. Ballhausen, H. Gray, Inorg. Chem. , 1 (1), 1962, pp 111-122

Retrieved from "https://chemwiki.ch.ic.ac.uk/index.php?title=Rep:Mod:TF910&oldid=818012"