Rep:Mod:TBFA2017
Molecular Modelling using Gaussian Software
Using Gaussview molecules of ammonia, hydrogen and nitrogen were built, optimised and their physical properties were studied.
NH3 Optimisation
Ammonia has the molecular formula of NH3 and is formed from the reaction between gaseous nitrogen, N2 and hydrogen, H2 in a process known as the Haber Bosch process. The equation for this reaction is:
N2 + 3 H2 → 2 NH3
A molecule of ammonia, NH3 was modelled using Gaussian software. the point group of the molecule was set to C3v. The molecule was then optimised with the calculation method set to RB3LYP and a basis set of 6-31G(d,p). The RMS gradient norm of the optimised product was 0.00000485 a.u. The final energy [E(RB3LYP)] of the ammonia molecule was -56.55776873 atomic units (a.u.). The molecule consists of 1 nitrogen atom covalently bonded to 3 separate hydrogen atoms. The nitrogen to hydrogen bonds are all single bonds with a bond length of 1.01798 angstroms. From the use of gaussian the bond angle of the H-N-H bond in ammonia was determined to be 106.7°C. Ammonia has a triangular planar shape with 3 bonding pairs and 1 lone pair of electrons around the central nitrogen atom. The lone pair of electrons repel more than than the bonding pairs which reduces the bond angle to 106.7°C.
The item table below is taken from the .*log file of the gaussian calculations for optimisation and from it we can see that the forces are all converged. The full optimisation file is liked to here
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
Below shows a jmol model of the molecule of ammonia built on gaussian:
Optimization of NH3 molecule |
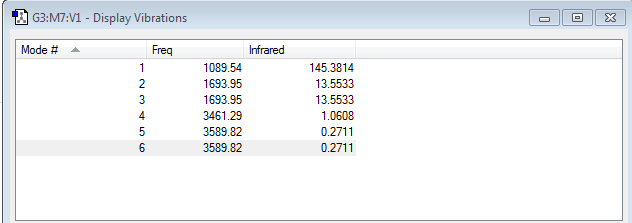
Vibration Analysis
By looking at the second derivative of the potential energy curve for ammonia (ie the curvature of the graph) we can determine the frequencies of the different modes of vibrations of the ammonia molecule. From the 3N-6 rule, we can expect there to be 6 modes of vibrations. Gaussian confirmed this by giving 6 frequencies of vibrations which are shown in the image above. Modes 2 and 3 have the same frequency of 1693.95 s-1 and modes 5 and 6 also have the same frequency of 3589.82 s-1. Since frequency is proportional to energy, the pairs of modes must also have the same energy. Thus these modes are degenerate. Of the 6 modes, modes 1,2 and 3 are bending vibrations i.e the vibrations cause a change in bond angle. Modes 4, 5 and 6 are examples of bond stretching vibrations which are vibrations which cause the bond length to change. The 4th mode which has a frequency of 3461.29 s-1 is a vibration that causes all the vibrating N-H bonds to stretch out and back in phase with each other and so this mode is highly symmetric. Mode 1 is a bending vibration and it is known as the umbrella mode. There are four different frequencies at which the bonds in ammonia vibrate and thus we would expect to see 4 bands in an experimental spectrum of gaseous ammonia, with each band corresponding to one frequency.
Charge Analysis
Nitrogen is a highly electronegative atom and so can attract the bonding electrons of the N-H bonds towards itself and away from the less electronegative hydrogens. This should result in the nitrogen having a slightly negative charge distribution leaving the electron efficient hydrogens with a slightly positive charge. Using gaussian the charges of the atoms were determined. The nitrogen atom had a charge of -1.125 and on each of the hydrogen atoms the charge was +0.375. These charge distributions are in accordance with our expectations.
Optimization of N2
Nitrogen, N2 exists as a diatomic molecule with two nitrogen atoms triple bonded covalently to each other. Nitrogen is a linear molecule and thus a bonding angle of 180°C. Below is a Jmol image of a nitrogen molecule:
Nitrogen molecule |
Since it is a linear diatomic nitrogen has D∞ symmetry. the bond length of the triple bond in the nitrogen molecule is 1.10550 angstroms. A molecule of nitrogen was built and optimised with the calculation method set to RB3LYP and a basis set of 6-31G(d,p). The RMS gradient norm of the optimised product was 0.00000060 a.u. The final energy [E(RB3LYP)] of the nitrogen molecule was -109.52412868 atomic units (a.u.).
Below is the item table taken from the full optimisation file which is linked here. The forces are all converged and so optimisation is complete and correct.
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
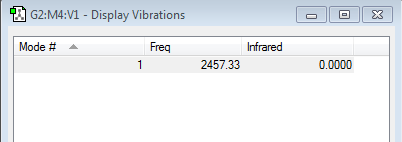
Vibration Analysis
Nitrogen is diatomic and thus the 3N-6 rule is adapted to 3N-5. Using this rule we can expect nitrogen to have one vibration mode. The frequency of this mode is shown in the image above. This mode is a stretching vibration. The triple bond of the nitrogen molecule stretches and shortens at a frequency of 2457.33 s-1.
Charge Analysis
Both the nitrogen atoms have zero charge due to the fact that they both have the same electronegativity and so attract the bonding electrons to an equal degree.
Optimization of Hydrogen molecule
Hydrogen is a diatomic molecule that consists of two hydrogen atoms covalently bonded to each other. Below is a jmol image of a hydrogen molecule:
Hydrogen molecule |
The bond between the two hydrogens is a single bond with a length of 0.74279 angstroms. the hydrogen molecule is a linear molecule and thus has a bonding angle of 180°C and has a D∞H symmetry. A molecule of hydrogen was built and optimised with the calculation method set to RB3LYP and a basis set of 6-31G(d,p). The RMS gradient norm of the optimised product was 0.00000017 a.u. The final energy [E(RB3LYP)] of the hydrogen molecule was -1.17853936 atomic units (a.u.).
In the item table below taken from the optimisation .*log file (the full file is linked here ) and it tell us that the optimisation was complete as all the forces converged.
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
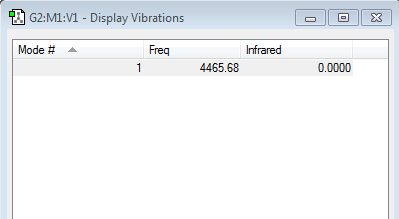
Vibration Analysis
Applying the 3N-5 rule for diatomic molecules to the hydrogen molecules shows that hydrogen should have one vibration mode. The details of this mode of vibration is shown above. This mode is a stretching vibration. The single covalent bond of the hydrogen molecule stretches and shortens at a frequency of 4465.68 s-1.
Charge Analysis
Both the hydrogen atoms have zero charge due to the fact that they both have the same electronegativity and so attract the bonding electrons to an equal degree.
Energy of Haber Bosch process
The Haber Bosch process uses nitrogen gas, N2), to produce ammonia, NH3), by reacting it with hydrogen gas, H2). The equation for this reaction is shown at the top of the page. From the energies determined after the optimisation of the ammonia, hydrogen and nitrogen molecules we can calculate the energy change in kJ/mol of the Haber Bosch process:
E(NH3)= -56.55776873 a.u. 2*E(NH3)= -113.1155375 a.u. E(N2)= -109.52412868 a.u. E(H2)= -1.17853936 a.u. 3*E(H2)= -3.53561808 a.u.
[E(X) means energy of molecule X]
ΔE=2*E(NH3)-[E(N2))+3*E(H2))]= -113.1155375 -(-109.52412868-3.53561808) = -0.05579074 a.u.
Converting the energy from atomic units change, the energy change of this reaction is -146.4785879 kJ/mol, and for the production of one mole of ammonia is -73.2392935 kJ/mol. this is much higher than the literature value for the energy change of this process which is -45.8 kJ/mol.[1] Gaussian is less accurate for this type of calculation.
Both the reactants and the products in this reaction are highly stable. Nitrogen has a very strong triple bond which requires a lot of energy to break and so has a very high stability, higher than that of ammonia molecules which has only triple bonds in its molecule. Therefore nitrogen, a reactant, is more stable than the product.
Choice of Own Small Molecule: Fluorine
Fluorine is a diatomic molecule that consisted of two fluorine atoms covalently bonded together. The bond is a single bond with a length of 1.40281 angstroms. Fluorine is a linear molecule and thus has a bonding angle of 180°C and has a D∞H. A molecule of hydrogen was built and optimised with the calculation method set to RB3LYP and a basis set of 6-31G(d,p). The RMS gradient norm of the optimised product was 0.00007365 a.u. The final energy [E(RB3LYP)] of the nitrogen molecule was -199.49825218 atomic units (a.u.).
Below is the item table taken from the full optimisation file which is linked here. The forces are all converged and so optimisation is complete and correct.
Item Value Threshold Converged? Maximum Force 0.000128 0.000450 YES RMS Force 0.000128 0.000300 YES Maximum Displacement 0.000156 0.001800 YES RMS Displacement 0.000221 0.001200 YES
Here is a Jmol image showing a molecule of fluorine:
Fluorine molecule |
Vibration Analysis
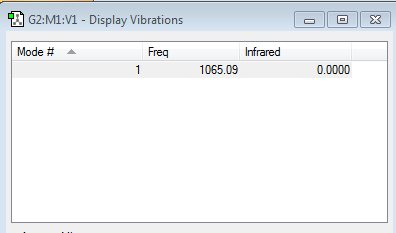
Fluorine is diatomic and thus the 3N-6 rule is adapted to 3N-5. Using this rule we can expect fluorine to have one vibration mode. The frequency of this mode is shown in the image above. This mode is a stretching vibration. The single covalent bond of the fluorine molecule stretches and shortens at a frequency of 1065.09 s-1.
Charge analysis
Both the fluorine atoms have zero charge due to the fact that they both have the same electronegativity and so attract the bonding electrons to an equal degree.
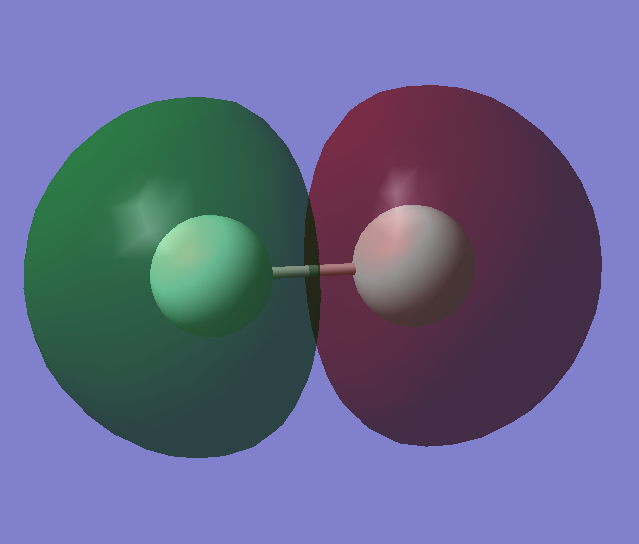
Molecular Orbitals of Fluorine
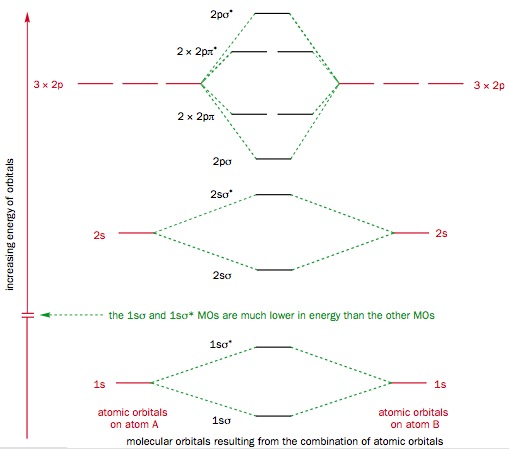
Fluorine atoms have an electronic configuration of 1s22s22p5. When two fluorine atoms combine to form F2 the atomic orbitals in the atoms combine to from molecular orbitals. Below is the molecular orbital diagram of fluorine:
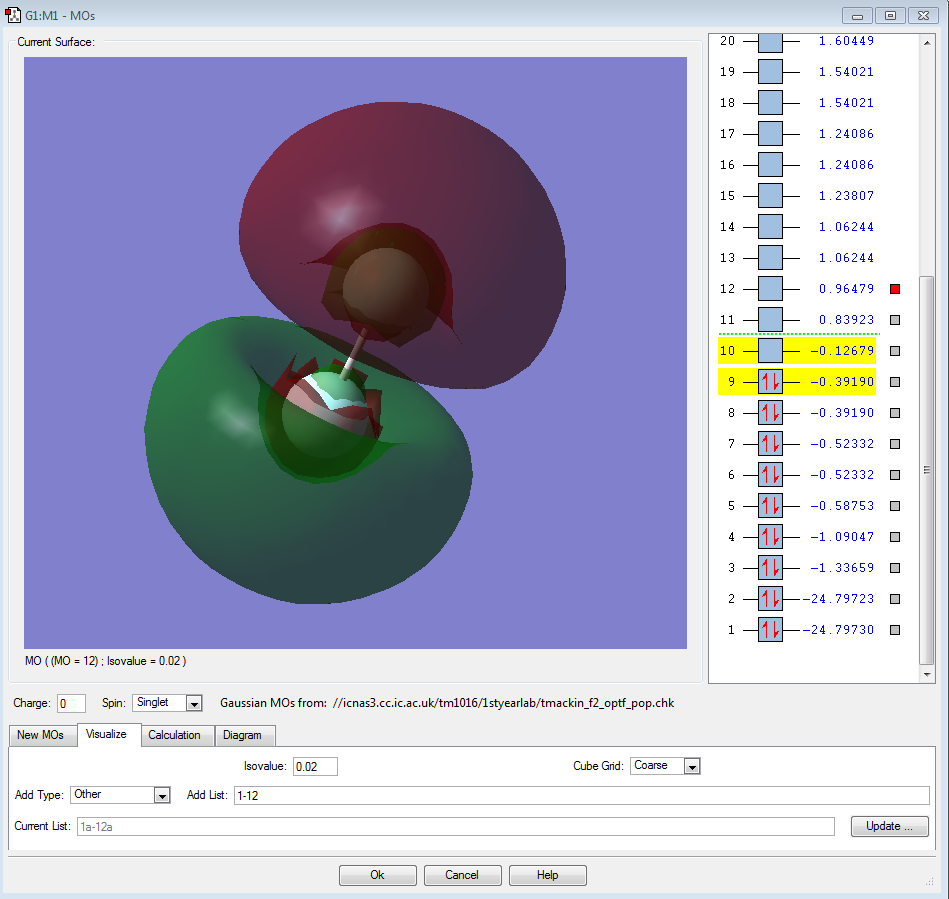
The screenshot below shows the energy values of each energy level:
[2]
Lowest Occupied Orbital
The first two orbitals are the lowest occupied orbitals and they represent the area where the 1s electrons orbit. These molecular orbitals are the 1s atomic orbital of each fluorine atom combined: the second orbital is the anti-bonding combination and the first is the bonding combination. These orbitals are held very tightly to the nucleus of each atom and thus are not involved during bonding. The energy of the first orbital is -24.79730 a.u. and the second is -24.79732 a.u.
3rd and 4th Molecular Orbitals: the 2σg orbitals
The energy of the 3rd molecular orbital is -1.33659a.u. and the energy of the 4th molecular orbital is -1.09047 a.u. These energies are different and thus these orbitals are non degenerate. These molecular orbitals are formed from when the 2s valence atomic orbitals of the fluorine atoms are combined. The 3rd molecular orbital is the bonding combination and the 4th is the anti-bonding combination. There is a lot of overlap in the molecular orbitals and so the energy of these orbitals is higher.