Rep:Mod:Sth13
.log Files can be found here.
Transition States are particular configurations of molecules which correspond to the highest energy point on a reaction coordinate, forming in between the reactant and product molecules. Having the highest potential energy means they are often short-lived and therefore cannot be isolated using experimental techniques. However they offer important insights into how chemical reactions proceed, and can be used to help explain the shape and geometry of the product molecule as well as the reaction pathway and the energy barrier. [1]
Computationally it is possible to generate transition state structures by exploiting Quantum Mechanical theory. This involves numerically solving the Schrödinger equation and using molecular orbital (MO) theory to predict the transition state structure, the corresponding energy and many other factors. In this computational study, the transition states for the Pericyclic Cope and Diels-Alder reactions are investigated. In the former the different energy conformations of the starting materials are computed and analysed; whereas in the latter case endo and exo selectivity is explored through generation of the two transition states corresponding to each of these distinct pathways.
The Gaussian computational program is used to undertake these calculations, and the calculations are mainly based on the Hartree-Fock (HF) and Density Functional Theory (DFT) level of theories. Although comparable, there are some differences between these two methods. Both are applicable when considering multi-electron systems; however, Hartree-Fock uses a simpler approach to the analysis, while Density Functional Theory uses information regarding electron density (based on Kohn-Sham theory) to evaluate energies, therefore offering a more rigorous analysis, but more computationally demanding. [2]
Nf710 (talk) 09:34, 18 January 2016 (UTC)Z Nice introduction but brief on the HF side of things, its solves the shrodinger equation using a slater determinant which expresses every configuration of electrons while obeying the antisymmetry principle from the pauli exclusion principle
Tutorial: The Cope Rearrangement

The Cope rearrangement belongs to a class of chemical reactions named Pericyclic reactions. Specifically a [3,3] sigmatropic shift, this proceeds via a concerted mechanism whereby bonds are formed and broken at the same time. Historically this reaction was subject to much controversy regarding the pathway the reaction takes. [3] It has now been accepted the the rearrangement proceeds via a so called ''Boat'' or ''Chair'' transition state structure. The Cope rearrangement of 1,5-hexadiene will be considered here. Computational calculations using Gaussian will be used to calculate which of these transition states is of the lowest energy, and will therefore correspond to the actual reaction pathway taken.
Optimising Reactants and Products
1,5-Hexadiene contains an sp3 carbon-carbon single bond. As such, there is free rotation around this bond leading to various possible conformations of the molecule. These can be classified as either antiperiplanar (anti) or synperiplanar (gauche). Examples of both conformers were drawn on Gaussian and subsequently optimised using the different levels theory previously discussed: Hartree Fock (HF/3-21G) and also Density Functional Theory (DFT/B3LYP/6-31G*).
1,5-Hexadiene Antiperiplanar Conformers
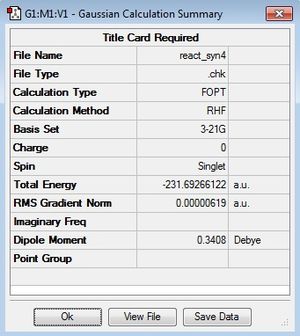
Firstly, GaussView was used to draw an anti-conformer of 1,5-hexadiene, with a dihedral angle of 180 degrees. The molecule was firstly cleaned using the 'Clean' function. This serves to alter the geometry of the molecule so as to more closely resemble the actual structure. This cleaned structure was then optimised under the Hartree-Fock method with a 3-21G basis set, so as to ascertain the energy and the point group. The energy was found to be -231.69097054 a.u. The 'Symmetrise' function was then used to ascertain the point group, this was found to be C1. Comparison with data in the Appendix 1 indicates this is the Anti4 conformer. The structure and results are summarised in the table below.
| Summary of Data | GaussView Structure | Point Group | ||
|---|---|---|---|---|
 |
C1 |
1,5-Hexadiene Gauche Conformers
Next, GaussView was used to draw a gauche-conformer of 1,5-hexadiene. The molecule was again cleaned and optimised using the same level of theory as above. The energy of this conformer was found to be -231.68771610 a.u. with a point group of C2. This corresponds to the Gauche conformer in the Appendix. The energy of this gauche conformer is higher than that of the anti4 conformer above; this is to be expected due to the increased steric clash between the two carbon-carbon double bonds in the gauche conformer. The structure and results are summarised in the table below.
| Summary of Data | GaussView Structure | Point Group | ||
|---|---|---|---|---|
 |
C2 |

The gauche3 conformer of 1,5-hexadiene was next drawn using GaussView. Following the same procedure as before the energy was found to be -231.69266122 a.u. and the point group C1 in accordance with the Appendix, confirming the molecule is gauche3. Surprisingly, this turns out to be the lowest energy conformer of 1,5-hexadiene, therefore suggesting this is the conformer which is preferred for the Cope rearrangement. This goes against the chemical intuition based on arguments of increased steric clash resulting in an corresponding increased energy. This result can be explained by consideration of the stereoelectronic interactions in the HOMO molecular orbital of the conformer. There is a favourable orbital overlap between the π orbitals of the two terminal C-C double bonds; according to Deslongchamps' theory, a favourable orbital overlap may lead to a conformational preference. This interaction is shown in the image of the HOMO here.
Nf710 (talk) 09:38, 18 January 2016 (UTC) Good use of the orbitals to show the overlap
| Summary of Data | GaussView Structure | Point Group | ||
|---|---|---|---|---|
 |
C1 |
1,5-Hexadiene anti2 Conformation HF/3-21G
A structure for the anti2 conformer was drawn, cleaned and optimised using the above theoretical approach. The energy was found to be -231.69253528 a.u. and the point group Ci in accordance with the Appendix.
| Summary of Data | GaussView Structure | Point Group | ||
|---|---|---|---|---|
 |
Ci |
i) Re-Optimisation HF/3-21G and B3LYP/6-31G*
The optimised anti2 structure was then re-optimised at a higher level of theory: Density Functional Theory (DFT/B3LYP/6-31G*). The energy was found to be -234.61171063 a.u. and the point group again Ci. The energy results between the two levels of theory cannot be compared; the DFT methodology uses spin and pairing energies in its calculations to find a better estimate for the conformer's actual energy and the results are not comparable. The two optimised structures can be compared in terms of geometry however, notably comparison of bond lengths and bond angles. Only half of the values are included: this is due to the symmetry of the molecule as a result of the centre of inversion. Although the molecules look very similar, there are some small differences as summarised here:
| Level of Theory | Bond Lengths / Å | Bond Angles / ° | |||||
|---|---|---|---|---|---|---|---|
| C1-C2 | C2-C3 | C3-C4 | C1-C2-C3 | C2-C3-C4 | C1-C2-C3-C4 | C2-C3-C4-C5 | |
| HF/3-21G | 1.316 | 1.509 | 1.553 | 124.8 | 111.3 | 114.7 | 180.0 |
| DFT/6-31G* | 1.334 | 1.504 | 1.548 | 125.3 | 112.7 | 118.6 | 180.0 |
There is only a small discrepancy between the two structures, and this indicates that the Hartree-Fock level of theory (with fewer base sets and a lower computational cost) is sufficient to generate a good estimate of the actual structure data. The agreement of the data indicates that the two structures optimised at the different theoretical levels correspond to the same point on the Potential Energy Surface.
Nf710 (talk) 09:39, 18 January 2016 (UTC) good geom comparision and you have come to the correct concluion,
ii) Frequency Calculations
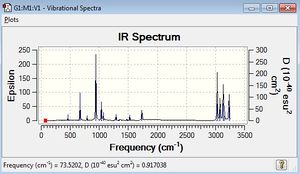
A frequency calculation was next carried out (again at the DFT/6-31G* level), so as to ensure the critical point on the Potential Energy Surface is a minimum and that all frequencies are real and there are no 'imaginary' (negative) frequencies. The lack of negative frequencies, as shown in the IR spectrum, indicate that this is not a transition state.

Also from the Frequency calculations, thermochemical data was acquired. This data is shown in the image below. The first sum value corresponds to the potential energy at 0 K, including the zero-point energy. The zero-point energy is a quantum mechanical concept, which describes the lowest energy state of a system that is possible. The application of the Harmonic Oscillator model to 1,5-hexadiene demonstrates that this low energy is due to residual energy caused by bond vibrations.
As such, the second calculation and the following calculations (now calculated at 298.15 K and pressure of 1 atmosphere) possess vibrational, rotational and translational energy contributions.
The third calculation value includes a correction for the RT term. If we consider H = E + RT, at 0 K it is evident that H = E. However, at 298.15 K, H ≠ E.
The final fourth calculation value considers the entropic contribution to the Gibbs Free Energy (G = H - TS). N.B. The calculation is carried out at a constant pressure of 1 atmosphere, as the temperature increases so will the enthalpy, according to basic thermodynamic principles.
The use of Statistical Mechanical concepts such as the partition function are taken into account in the Gaussian calculations in order to provide the best possible estimate of the Thermochemical data. [4]
Nf710 (talk) 09:41, 18 January 2016 (UTC) Good level of understanding. The frequencies are actually imaginary however guassian just says that they are negative.
''Chair'' and ''Boat'' Transition Structure Optimisation
Here the possible transition structures in the Cope rearrangement are examined. As previously discussed, the reaction proceeds via cyclic transition state, either a ''chair'' or a ''boat''. Different computational analytic techniques will be used to evaluate which provides the best estimate for the transition state. In addition to an evaluation of different techniques, the IRC (Intrinsic Reaction Coordinate) and the Activation Energies for the transition states will be calculated and examined.
The 'local search' methodology was used, in which a guess for the transition structure is firstly created. This method relies on the guess being close to the actual transition state structure or else the calculation will fail. This information is then used to calculate the Hessian (Force Constant Matrix) which is then updated continually as the computation continues. Applying this method involved drawing two C3H5 allyl fragments (optimising them under HF/3-21G level of theory), and positioning them 2.2 Å apart (the symmetrise function was used here). They were of different point group symmetry: one C2H and one C2V.
Chair Optimisation with Force Constant Calculation
A Gaussian optimisation was set up for a transition state - this is typically more difficult than a minimisation as the calculation requires knowledge of the reaction coordinate. The optimisation was to a TS (Berny), calculating the force constants once. The addition of Opt=NoEigen into the calculation intended to prevent the program crashing if more than one imaginary frequency was found. N.B. This is normally indicative of a poor structural guess for the transition structure. The resulting optimised structure provided one imaginary frequency at -817.96 cm-1. The one imaginary frequency confirms the structure is a transition state. We would expect the force constant to be negative as the force is contrary to the displacement of the molecule. In the Quantum Harmonic Oscillator model the force constant is a second derivative (a measure of the curvature of the Potential Energy Surface at that specific point), which is taken as a square root to obtain the frequency. The square root of a negative number is imaginary, and as such we expect a negative frequency. [5]
Nf710 (talk) 09:45, 18 January 2016 (UTC) And equation would have been nice here.
| Summary of Data | GaussView Structure | Calculated Frequencies | Imaginary Frequency Structure | ||||
|---|---|---|---|---|---|---|---|
 |
 |
Chair Optimisation using Frozen Coordinate Method
Another optimisation of the guess chair transition structure was investigated, however this time using the Frozen Coordinate method. Using the Redundant Coordinator Editor in GaussView the distance between the terminal allyl carbons in the two fragments was frozen at 2.17 Å apart. This method aims to remove certain degrees of freedom associated with molecules. The additional keywords Opt=ModRedundant were added, in order to remove any internal coordinates not needed in the calculation. The optimisation was then run under the HF/3-21G level of theory, optimising towards a TS (Berny). The energy was found to be -231.61932179 a.u. and again an imaginary frequency at -817.71 cm-1 confirming that a transition state has been formed. Direct comparison of the energies is possible in this case, as the same level of theory, and therefore basis sets, were used in each calculation. The energy difference between the two molecules optimised under the different techniques was found to be 0.0018 kJ/mol, which is a negligible energy difference here. The bond distances were also found to agree, which suggests the 'guess' chair transition structure was a good estimate of the actual transition state.
Boat Optimisation
In order to generate a transition structure for the boat conformer, the QST2 and QST3 methods can be used. These rely on using the reactant and product structures in order to estimate the transition state structure; in addition QST3 also needs a guess transition structure. Therefore, the reactant and product molecules were numbered so as to ensure GaussView could compute the exact carbon positions following the rearrangement. These labelled conformers are shown below.
Initially the optimisation failed, the resulting transition state structure resembled a chair more than a boat. However upon altering the bond angles of the reactant and product molecules to reflect more accurately the transition structure geometry the optimisation was successful.The energy value calculated: -231.60280230 a.u. and an imaginary frequency of - 840.51 cm-1. The vibration is shown below:
| Labelled Reactant Molecule | Labelled Product Molecule | Transition Structure | ||
|---|---|---|---|---|
 |
 |
An attempt at the QST3 methodology was undertaken, however, this optimisation was not found to be successful. It is presumed that this is due to large structural differences between the guess transition state structure and the actual structure.
Nf710 (talk) 09:46, 18 January 2016 (UTC)All your energies and frequencies are correct.
Intrinsic Reaction Coordinate Calculations
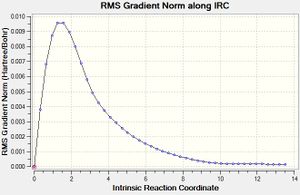
Although the above calculations confirm that both a chair and boat transition states are possible structures during the Cope rearrangement, they do not provide enough information to conclude which transition state is favoured. As such, an Intrinsic Reaction Coordinate (IRC) is used to decide, whereby Gaussian follows the minimum energy pathway from the transition state down the steepest gradient to its minimum on the Potential Energy Surface. [6] This is achieved by making small changes to the geometry at specific points along the gradient. Although it is possible to set the reaction coordinate in both directions, here it is acceptable to only follow it in one direction due to the symmetrical nature of the rearrangement. Additionally, the number of steps in the IRC can also be set manually, although if not enough steps are given a minimum will not be found and if too many are chosen an incorrect minima may be found. The force constant was calculated at each step because a frequency calculation had not been previously calculated. Although demanding on the software, this is often the most reliable choice and given the small nature of the system this option was taken.
Initially an IRC was run on the chair transition state, set to 50 steps, under the standard HF/3-21G level of theory. The IRC 'crashed' after 44 steps, and the energy level plateaued suggesting an energy minimum had been found. The energy at this 44th point was found to be -231.69157889 a.u. There are two possible ways to confirm that this is minimum:
i) Run an optimisation (HF/3-21G) on the final structure and find its energy. This was done and the resulting energy value was found to be: -231.69166512 a.u. This energy value corresponds to the lowest energy 1,5-hexadiene conformer examined earlier: the gauche2 conformer.
ii) Run an additional IRC with a larger number of steps, in order to ensure that there is not another minimum which lies lower in energy. It was chosen to do this with 70 steps. However, the reaction stopped at the same point (44) with the same energy value calculated. Therefore this method also confirmed this is the gauche2 conformer.
| IRC Graph (Total Energy) | IRC Graph (RMS Gradient Norm) | Reaction Coordinate |
|---|---|---|
 |
 |

|
Nf710 (talk) 09:48, 18 January 2016 (UTC) correct conformer identified. The IRC will always stops once it has met the limited of convergence.
Calculations for the Activation Energies
Finally, the activation energies for both the boat and the chair conformers were calculated. The activation energies were calculated for both structures under the two different levels of theory previously discussed: HF/3-21G and DFT/6-31G*. The initially optimised HF/3-21G structures were optimised under the latter technique so as to reduce the computational cost. The two methods are compared below quantitatively with reference to the geometry of the species and the energy values calculated.
This table summarises the bond distance between the transition state structures. C1-C1 represents the bond distance between the terminal carbon atoms on each fragment, and C1-C2 represents the bond distance between the terminal carbon atom and its nearest neighbour on one fragment. It is noted that the bond distances and geometries calculated are very similar between the two levels of theory.
| Level of Theory | Chair Conformer (Å) | Boat Conformer (Å) | ||
|---|---|---|---|---|
| C1-C1 | C1-C2 | C1-C1 | C1-C2 | |
| HF/3-21G | 2.021 | 1.390 | 2.140 | 1.381 |
| DFT/6-31G* | 1.968 | 1.407 | 2.207 | 1.393 |
In addition, the energy values for the different species can be compared.
| HF/3-21G | DFT/6-31G* | |||||
|---|---|---|---|---|---|---|
| Electronic energy (a.u.) | Sum of electronic
and zero-point energies (a.u.) |
Sum of electronic
and thermal energies (a.u.) |
Electronic energy (a.u.) | Sum of electronic
and zero-point energies (a.u.) |
Sum of electronic
and thermal energies (a.u.) | |
| Chair Transition State | -231.61932246 | -231.466700 | -231.461341 | -234.55693093 | -234.414910 | -234.408982 |
| Boat Transition State | -231.60280230 | -231.450926 | -231.445298 | -234.54309298 | -234.402341 | -234.396006 |
| Anti2 Conformer | -231.69253528 | -231.539539 | -231.532565 | -234.61171063 | -234.469219 | -234.461869 |
Consideration of the activation energy of each conformer is also of importance in considering the reaction pathway. The activation energy can be defined as the minimum energy requirement for a reaction to happen; a energetic barrier which the molecules must pass over in order to react. [7] Here, the activation energy can be calculated by taking the difference between the transition state energies and the reactant (anti2) energy. This can be calculated at different temperatures by using the different thermochemical data generated by Gaussian: 0 K (using the sum of electronic and zero-point energies) and 298.15 K (by using the sum of electronic and thermal energies). The activation energies were converted from Hartrees to kJ/mol using the conversion factor 1 Hartree = 2600 kJ/mol.
| HF/3-21G | DFT/6-31G* | Experimental [8] | |||
|---|---|---|---|---|---|
| 0 K | 298.15 K | 0 K | 298.15 K | 298.15 K | |
| Chair Transition State | 191.23 kJ/mol | 187.00 kJ/mol | 142.59 kJ/mol | 138.85 kJ/mol | 140±2 kJ/mol |
| Boat Transition State | 232.65 kJ/mol | 229.12 kJ/mol | 175.59 kJ/mol | 172.92 kJ/mol | 187.1±8 kJ/mol |
The results demonstrate that at both levels of theory, and at both temperatures, the chair transition state structure has the lower activation energy. There is however, a large discrepancy between the values calculated at the different levels of theory. In order to decide which level of theory offers the best estimate of the activation energy, these numbers should be compared to experimental data. It is clear from comparison with the experimental data that the DFT/6-31G* level of theory offers the best estimate of activation energy. We can conclude that the two levels of theory hold quite different values. If interested in geometries (bond lengths, angles etc) it is apparent that the lower level (HF/3-21G) offers a viable estimate of the data. This may be favourable sometimes as it is less computationally demanding. However, when considering energetic data, for example as the activation energy has been considered above, it is clear that the computationally more demanding level of theory (DFT/6-31G*) offers the most accurate estimate when compared to literature values. The differences between the calculations may arise due to the numerous approximations the Gaussian program makes when calculating, and the fact that only one single molecule is considered (in reality, a single molecule is never experimented on, rather intermolecular forces will be present and therefore affect the data).
Nf710 (talk) 09:54, 18 January 2016 (UTC) In general this is a very good report, you have done everything that has been asked of you to a good extent, however you could have show a bit more understanding of the theory and how the various levels of theory work. Also well done for doing it in kcal.
Exercise: The Diels-Alder Cycloaddition

The Diels-Alder reaction is the most famous example of the cycloaddition class of pericyclic reactions. This single step concerted reaction proceeds simply by heating, forming a six-membered ring structure, via a cyclic transition state. Commonly referred to as a [4+2]-cycloaddition, the two components of the reaction are named the diene and the dienophile; whereby the π orbitals of the dienophile are used to form new σ bonds with the π orbitals of the diene. [9] The reaction is not usually reversible, due to the strength of the new σ bonds formed and the thermodynamic stability associated with the 6 membered ring structure generated.
The 'allowedness' of the reaction stems from the number of electrons involved in the reaction mechanism and whether the HOMO and LUMO interactions are favourable or not. The Diels-Alder reaction can be further sub-categorised into either normal electron demand or inverse electron demand.
(Perhaps more fundamentally, the symmetries of the interacting orbitals must be the same for a non-zero overlap Tam10 (talk) 16:37, 10 January 2016 (UTC))
i) Normal Electron Demand - the main interactions are between the HOMO of the diene and the LUMO of the dienophile. This is usually aided by electron donating groups (EDGs) on the diene to raise the energy of the HOMO and electron withdrawing groups (EWGs) on the dienophile to lower the energy of the LUMO. This results in a better orbital overlap, resulting in a more favourable reaction.
ii) Inverse Electron Demand - the EDGs and EWGs are placed counter-intuitively on the opposite substituent to before. i.e. the diene has an EWG and the dienophile has an EDG. This again has the effect of lowering the orbital energy between the HOMO and LUMO so as to produce a more favourable orbital overlap and facilitate the reaction.
Therefore, there are many factors to consider before undertaking a Diels-Alder reaction. Organic Chemists often make use of a set of governing rules to predict reactivity of reactants: the Woodward-Hoffmann rules: (4q + 2)s and (4r)a where q and r are integer values and s = suprafacial and a = antarafacial. This argument is based on Frontier Molecular Orbital theory and is a useful tool for experimental Organic Chemists.
Perhaps the most useful aspect of the Diels-Alder reaction is the well understood regiochemical (and often stereochemical) outcomes which arise from an in-depth understanding of the cyclic transition state structure. The so called 'endo' effect describes the preference for Diels-Alder cycloadditions to adopt the 'endo' like transition state resulting in the kinetic endo product, as opposed to the 'exo' like transition state which results in the thermodynamic eco product. The relatively straightforward reaction conditions used in the Diels-Alder reaction therefore offer chemists the ability to rapidly make complex regiospecific ring systems with ease. Using the Gaussian program, two Diels-Alder reactions will be studied in order to better understand the cyclic transition states generated in the reaction mechanism.
Reaction of cis-Butadiene with Ethene
A molecule of cis-butadiene was drawn using the GaussView program. The molecule was firstly 'cleaned', the point group set to C2V, and then optimised using the AM1 semi-empirical molecular orbital method. The HOMO and LUMO were then analysed and plotted on cartesian coordinates, so as to better understand their symmetry. These orbitals are shown below. It was found that HOMO is antisymmetric about the XY and YZ plane; the LUMO is symmetric about the XY and YZ plane.
(In this case, it's the yz plane symmetry that's important for the reaction. Both the LUMO and HOMO are antisymmetric about the xy plane Tam10 (talk) 16:37, 10 January 2016 (UTC))
| HOMO of cis-Butadiene | LUMO of cis-butadiene |
|---|---|
 |
 |
Computation of the Transition State for the Reaction of cis-Butadiene with Ethene
A molecule of ethene was drawn using the Gaussian program, and again 'cleaned' and optimised under the same level of theory (AM1 semi-empirical). Similar to previously described attempts to find the transition state structure above, a 'guess' transition state structure was drawn. In this particular example there are no regioselectivity issues. The diene (cis-Butadiene) and dienophile (ethene) were set 2.23 Å apart, and the 'guess' structure was optimised under the same level of theory. This calculation encountered an error; as such it was decided to use the Frozen Coordinate Method in order to aid the computation. The distance between the terminal carbons of the ethene and the π system in the cic-butadiene were frozen at the distance 2.23 Å and optimised to a minimum. The Frozen coordinates were then removed and a further optimisation to a TS (Berny) was calculated. This produced an optimised transition state, as proven by the presence of one imaginary frequency vibration. The energy was found to be 0.11165469 a.u. with the imaginary frequency at -956.35 cm-1.
| Transition State Structure and Animation | Imaginary Frequency Vibration | |||||
|---|---|---|---|---|---|---|
Analysis of HOMO
The reaction can be further probed by consideration of the HOMO and LUMO orbitals of the transition state as shown below, particularly distinguishing between normal electron demand and reverse electron demand. In this case, the HOMO of the diene (cis-butadiene) is of a higher energy than the HOMO of the dienophile (ethene) and we can class this as a normal electron demand reaction. The HOMO of the diene and the LUMO of the dienophile interact to give the symmetric transition state LUMO. The LUMO of the diene and the HOMO of the dienophile interact to give the unsymmetric transition state HOMO. The transition state orbitals are shown in the table below, with Cartesian coordinates for reference.
(Unsymmetric/asymmetric =/= antisymmetric Tam10 (talk) 16:37, 10 January 2016 (UTC))
| HOMO of Transition State | LUMO of Transition State |
|---|---|
 |
 |
Intrinisic Reaction Coordinate Calculations
| IRC Graph (Total Energy) | IRC Graph (RMS Gradient Norm) | Reaction Coordinate |
|---|---|---|

|

|
|
(There is more to be done in this section. Refer to the Discussion section Tam10 (talk) 16:37, 10 January 2016 (UTC))
Reaction of Cyclohexa-1,3-diene with Maleic Anhydride
Now the Diels-Alder reaction between the diene Cyclohexa-1,3-diene with the dienophile Maleic Anhydride is investigated. This normal electron demand reaction is perhaps more interesting than the previously explored Diels-Alder due to the added complexity of regiochemical products: exo and endo. This arises as a result of the antisymmetric nature of the reaction and so called secondary orbital interactions resulting in the preferred 'endo' product. This is commonly referred to as the 'endo' rule. This Diels-Alder reaction is particularly efficient due to the electron poor alkene in maleic anhydride (this is a result of the electron withdrawing carbonyl groups present).
i) Exo Transition State
A 'guess' transition state structure of the exo conformer was drawn, following optimisation of the two reactant molecules under the AM1 Semi-Empirical level of theory. The exo transition state was then frozen 2.22 Å, optimised to a minimum, unfrozen, optimised to a TS (Berny), and then optimised again to get a .log file. The energy of the transition state was found to be -0.05041983 a.u. with an imaginary frequency at -812.25 cm-1. And point group Cs.
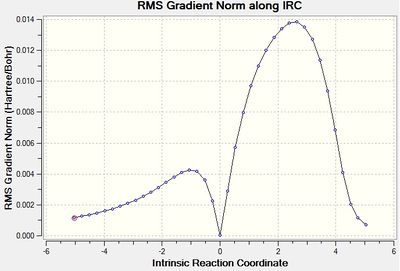
| Transition State Structure and Animation | IRC Graph (Total Energy) | IRC Graph (RMS Gradient) | Imaginary Frequency Vibration | ||||
|---|---|---|---|---|---|---|---|

|
|
The minimum found in the IRC RMS graph shows that a transition state has been found. It is also worth considering the transition state geometry i.e. bond lengths. the C1-C2. C5-C6, C2-C5, C15-16 bond distances are on average intermediate of those between an sp3 (1.54 Å) and an sp2 (1.34 Å) C-C and C=C bond. [10] This is a promising result, as we would expect these bond distances to be of intermediate value given they are either breaking/forming in the concerted Pericyclic mechanism. Furthermore, the C6-C16 and C1-C15 distances can be compared to 2 x the Van der Waals radii. It was calculated that these distances are smaller than the value, which suggests there is a favourable interaction between them, again as would be expected for this transition state.

| Exo Transition State Bond Lengths (Å) | ||||||
|---|---|---|---|---|---|---|
| C1-C2 | C5-C6 | C2-C5 | C6-C12 | C9-C12 | C15-C16 | C6-C16 |
| 1.394 | 1.394 | 1.397 | 1.490 | 1.522 | 1.410 | 2.170 |
(What about C19-H14, regarding sterics? Tam10 (talk) 16:37, 10 January 2016 (UTC))
| LUMO +1 | LUMO | HOMO |
|---|---|---|
 |
 |
 |
The key orbitals corresponding to the Exo transition state are shown above. Both the HOMO and LUMO are antisymmetric. It can be shown that there is only primary and not secondary orbital interactions here, due to the distance between the C=C π and C=O π* antisymmetric orbitals being too far apart for any good interaction. As such, we can rationalise that the exo transition state is higher in energy as it does not have any supportive secondary orbital interactions.
ii) Endo Transition State

As for above, a 'guess' endo conformer was drawn and subjected to the previously discussed conditions. The energy of the transition state was found to be -0.05150480 a.u. with an imaginary frequency -806.87 cm-1. And point group Cs.
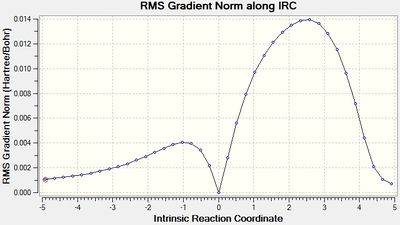
| Transition State Structure and Animation | IRC Graph (Total Energy) | IRC Graph (RMS Gradient) | Imaginary Frequency Vibration | ||||
|---|---|---|---|---|---|---|---|

|
|
The minimum found in the IRC RMS graph shows again that a transition state has been found. As above, the transition state geometry can be better understood through evaluation of the bond distances. It is again shown that the bonds being broken/formed are intermediate of the sp3 and an sp2 C-C and C=C bond
| Endo Transition State Bond Lengths (Å) | |||||
|---|---|---|---|---|---|
| C1-C2 | C5-C6 | C2-C5 | C9-C12 | C15-C16 | C1-C15 |
| 1.393 | 1.393 | 1.397 | 1.523 | 1.408 | 2.162 |
| LUMO +1 | LUMO | HOMO |
|---|---|---|
 |
 |
 |
The key orbitals corresponding to the endo transition state are shown above. Both the HOMO and LUMO are antisymmetric, as for the exo transition state. However, contrary to the exo transition state orbitals analysed above, here there is significant interaction between the C=O π* orbitals in maleic anhydride and the C=C π orbitals of cyclohexa-1,3-diene. This secondary orbital overlap explains why the endo transition state is lower in energy and is therefore kinetically favoured over the exo transition state.
iii) Analytic Comparison of key MOs, Activation Energies and Stability
In order to deduce which structure is favoured in this Diels-Alder reaction, the activation energies for the processes were analysed. This was again calculated by consideration of the energetic differences between the starting materials and the transition state structures, and converted into more meaningful units of kJ/mol.
| Energy | ||||||
|---|---|---|---|---|---|---|
| Maleic Anhydride (a.u.) | Cyclohexa-1,3-diene (a.u.) | Sum of Reactants (a.u.) | Transition Structure (a.u.) | Activation Energies (kJ/mol) | ||
| Exo | Endo | Exo | Endo | |||
| -0.12182418 | 0.02771128 | -0.0941129 | -0.05041983 | -0.05150480 | 114.72 | 111.87 |
It can therefore be seen that the endo transition state has a lower activation energy, and is therefore the kinetic product. The exo conformer has a higher activation energy, which can be explained by the increased steric hindrance this molecule experiences due to the clash between the oxygen groups and the alkyl groups. The endo product does not experience these effects.
Conclusion
To conclude, the transition states of three pericyclic reactions were studied computationally: the Cope rearrangement of 1,5-Hexadiene and the Diels-Alder reactions of cis-Butadiene with Ethene and Cyclohexa-1,3-diene with Maleic Anhydride.
The different conformers of 1,5-Hexadiene were first studied: optimised under the HF/3-21G level of theory and their energy values evaluated. This resulted in the surprising conclusion that the gauche3 conformer was of the lowest energy, although this was explained by the stabilising stereoelectronic arguments found in the HOMO interactions. The chair and boat transition state structures of the Cope rearrangement were next examined under two levels of theory (HF/3-21G and DFT/6-31G*). Both of these analytical techniques demonstrated that the chair structure was of lower energy. This is in agreement with experimental results from literature, with the latter level of theory providing a more closely matched value.
The Diels-Alder reactions were studied using a different level of theory: AM1 Semi-Empirical. Analysis of the key orbitals involved in these reactions demonstrated that they could be classified as normal electron demand reactions (with retention of orbital symmetry - therefore allowed), with the presence of imaginary (negative) frequencies used to justify the presence of a transition state structure. Equally so, a comparison of the transition structure bond lengths to those expected from a C-C sp3 and C=C sp2 bond agreed with this conclusion.
Analysis of the HOMO and LUMO of the two transition structures demonstrated the presence of secondary orbital interactions in the endo transition state, explaining why it is found at a lower energy and leads to the kinetically favoured product. Equally, one could argue that the presence of steric hindrance in the exo transition state leads this to be energetically higher and therefore unfavoured in the reaction coordinate.
In future, a wider variety of Diels-Alder reactions could be studied computationally and compared to experimental literature results. It is important to underline that all computations analysed through Gaussian make use of extensive assumptions and approximations (Born-Oppenheimer etc). They also only analyse a single molecule, which is not representative of real life experimentation. Use of different levels of theory, for instance DFT/6-31G*, could be used to further analyse expected transition states.
References
[1] Clayden, Greeves, Warren; 2012, Organic Chemistry, 2nd Edition, Oxford University Press
[2] Amusia, Msezane, Shaginyan; Physica Scripta; Vol T68, 2003, C133–140
[3] Imperial College London, Computational Chemistry Wiki. Accessed 14th December 2015 https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3#Appendix_1
[4] Joseph W. Ochterski, Thermochemistry in Gaussian, 2000. Accessed 14th December 2015 http://www.gaussian.com/g_whitepap/thermo/thermo.pdf
[5] E.G. Lewars, 2010, Computational Chemistry, 2nd Edition, Springer Science & Business Media
[6] Chaaban, Sezgin, On the Generalized Degreees of Freedom of the Gaussian Interference Relay Channel, IEEE Interactions on Information Theory, 58, 7, 2012
[7] Clayden, Greeves, Warren; 2012, Organic Chemistry, 2nd Edition, Oxford University Press
[8] N.J. Hoboken, 2007, Computational Organic Chemistry, John Wiley & Sons
[9] Nicolaou, Snyder, Montagnon, Vassilikogiannakis, The Diels-Alder Reaction in Total Synthesis, Angewandte Chemie, 41, 10, 2002
[10] Alkanes, Alkenes and Alkynes, Imperial College London Lecture Course, Professor Chris Braddock, January 2014
