Rep:Mod:Stella
Molecular Modelling 2
NH3 molecule
A computational analysis was performed on NH3 molecule with Gaussian calculation. The following table presents the information upon the completion of optimization and frequency analysis.
| Structure | ||
|---|---|---|
| ||
| Information | ||
| Molecule | NH3 | |
| Calculation Method | RB3LYP | |
| Basis Set | 6-31G(d,p) | |
| Final Energy E(RB3LYP) (a.u.) | -56.55776873 | |
| RMS gradient (Hartree/Bohr) | 0.00000485 | |
| Point Group | C3v | |
Completion of the Gaussian optimization process was ensured by checking with the Gaussian generated output data. The following table illustrates the results.
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES Predicted change in Energy=-5.986255D-10 Optimization completed. -- Stationary point found.
Since the values of the maximum force, RMS force, maximum displacement and RMS displacement were below their respective threshold values, it can be determined that for the optimized structure of NH3 molecule, the Gaussian calculation process was complete.
Subsequently, the bond length of the optimized CH4 molecule was calculated, which yielded a value of 1.09197Å. The H-C-H bond angle calculated was 109.471° and the torsion angle was 120°.
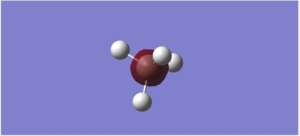
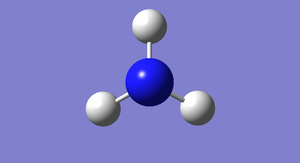
3D Structure
NH3 molecule |
Charge Distribution
Calculation of charge distribution of NH3 molecule was then performed following the optimization and frequency analysis. The diagram shows its charge distribution. The atoms are coloured according to the charge distribution.
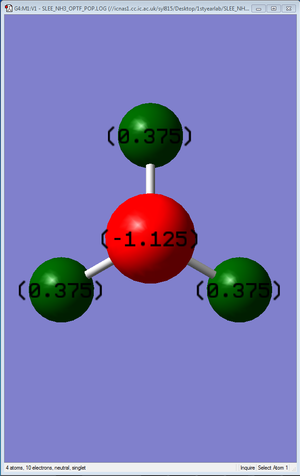
Interestingly, the charges of the Nitrogen atom is -1.125, and each Hydrogen atom, +0.375, as calculated by Gaussian. This differed from the expected values of -3 for the Nitrogen atom and +1 for each Hydrogen atom. A possible reason could be because the expected values are calculated based on the classical model, whereas the Gaussian calculations were performed using quantum mechanical calculations.
Vibrational and IR Analysis
Vibrational and IR analysis was subsequently performed on the final optimized structure of NH3 molecule. The following diagram summarizes the results obtained after the analysis.
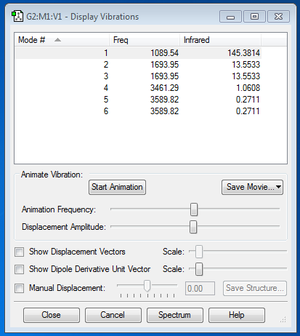
| How many modes do you expect from the 3N-6 rule? | 6 |
| Which modes are degenerate (i.e. have the same energy)? | Modes 2 and 3 Modes 5 and 6 |
| Which modes are "bending" vibrations and which are "bond stretch" vibrations? | “Bond stretch” vibrations: modes 4, 5 and 6 “Bending” vibrations: modes 1, 2 and 3 |
| “Bending” vibrations | modes 1, 2 and 3 |
| Which mode is highly symmetric? | Mode 4 |
| One mode is known as the "umbrella" mode, which one is this? | Mode 1 |
| How many bands would you expect to see in an experimental spectrum of gaseous ammonia? | 2 |
The following diagram presents the computationally calculated IR spectrum data for NH3 molecule.
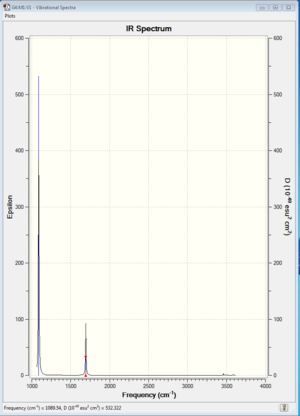
Prominent peaks were observed for mode 1 and modes 2 and 3, where the peaks for modes 2 and 3 could not be distinguished from each other due to the similarities in frequencies (1693.95 cm-1).
N2 molecule
A computational analysis was performed on N2 molecule with Gaussian calculation. The following table presents the information upon the completion of optimization and frequency analysis.
| Structure | ||
|---|---|---|
| ||
| Information | ||
| Molecule | N2 | |
| Calculation Method | RB3LYP | |
| Basis Set | 6-31G(d,p) | |
| Final Energy E(RB3LYP) (a.u.) | -109.52412868 | |
| RMS gradient (Hartree/Bohr) | 0.00000060 | |
| Point Group | D*H | |
Completion of the Gaussian optimization process was ensured by checking with the Gaussian generated output data. The following table illustrates the results.
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.401025D-13
Optimization completed.
-- Stationary point found.
Since the values of the maximum and RMS forces were below their respective threshold values, it can be determined that for the optimized structure of N2 molecule, the Gaussian calculation process was complete.
3D Structure
N2 molecule |
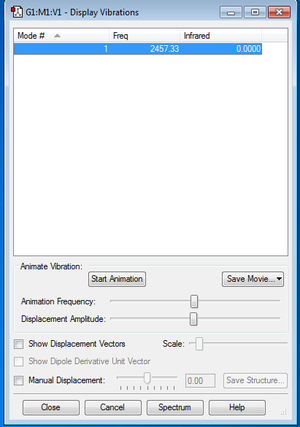
Vibrational and IR Analysis
Vibrational and IR analysis was subsequently performed on the final optimized structure of N2 molecule. The following diagram summarizes the results obtained after the analysis.
H2 molecule
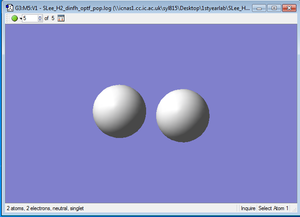
A computational analysis was performed on H2 molecule with Gaussian calculation. The following table presents the information upon the completion of optimization and frequency analysis.
| Structure | ||
|---|---|---|
| ||
| Information | ||
| Molecule | H2 | |
| Calculation Method | RB3LYP | |
| Basis Set | 6-31G(d,p) | |
| Final Energy E(RB3LYP) (a.u.) | -1.17853936 | |
| RMS gradient (Hartree/Bohr) | 0.00000017 | |
| Point Group | D*H | |
Completion of the Gaussian optimization process was ensured by checking with the Gaussian generated output data. The following table illustrates the results.
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
Since the values of the maximum and RMS forces were below their respective threshold values, it can be determined that for the optimized structure of H2 molecule, the Gaussian calculation process was complete.
3D Structure
H2 molecule |
File:SLEE H2 DINFH OPTF POP.LOG
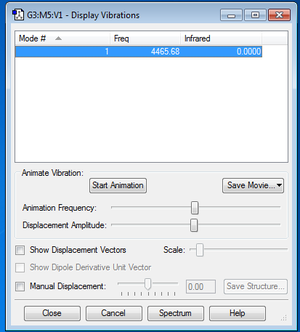
Vibrational and IR Analysis
Vibrational and IR analysis was subsequently performed on the final optimized structure of H2 molecule. The following diagram summarizes the results obtained after the analysis.
Haber-Bosch reaction energy calculation
E(NH3)= -56.55776873 a.u.
2*E(NH3)= -113.11553746 a.u.
E(N2)= -109.52412868 a.u.
E(H2)= -1.17853936 a.u.
3*E(H2)= -3.53561808 a.u.
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05579070 a.u.= -146.47 kJ/mol
Since the total enthalpy change calculated was a negative value, this indicated that the Ammonia product is more stable.
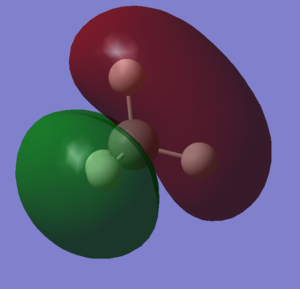
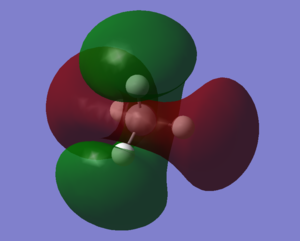
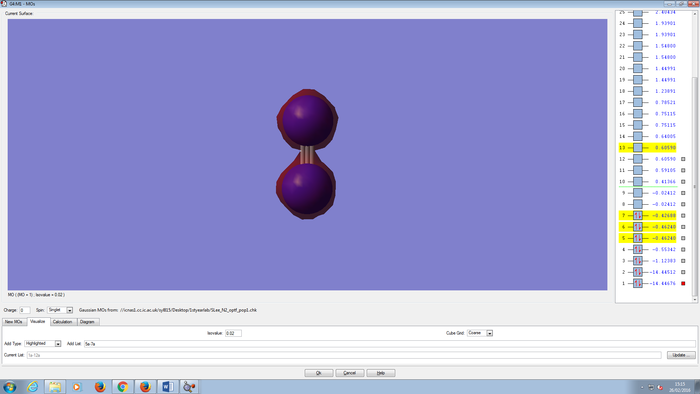
Molecular Orbitals Of N2 molecule
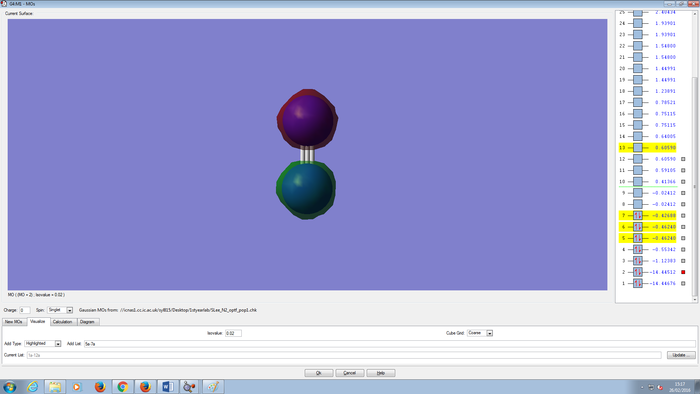
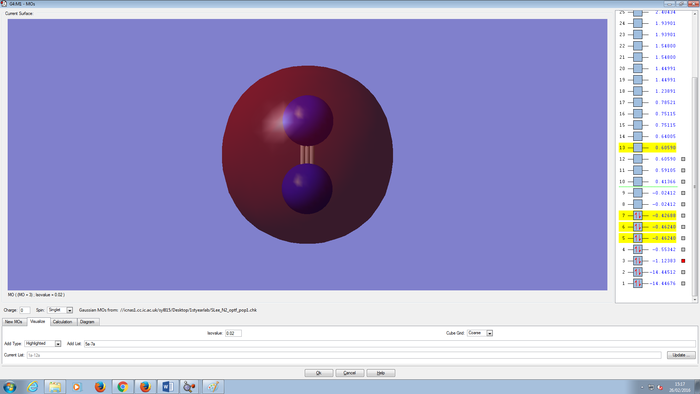
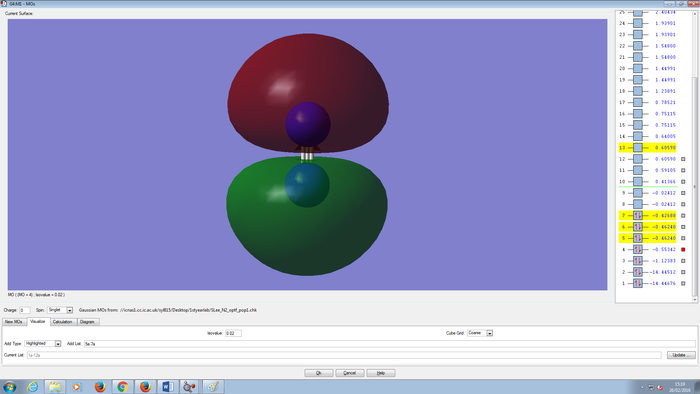
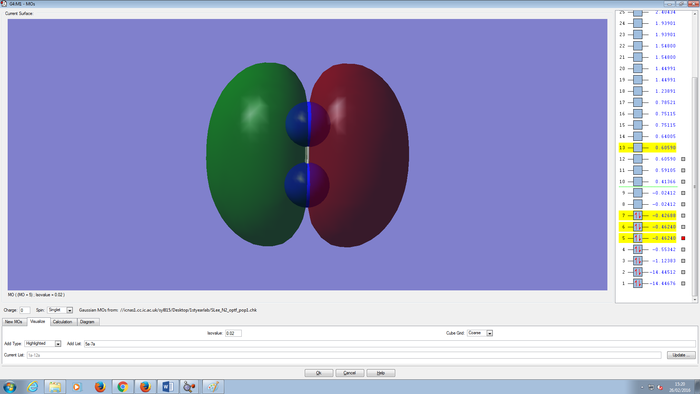
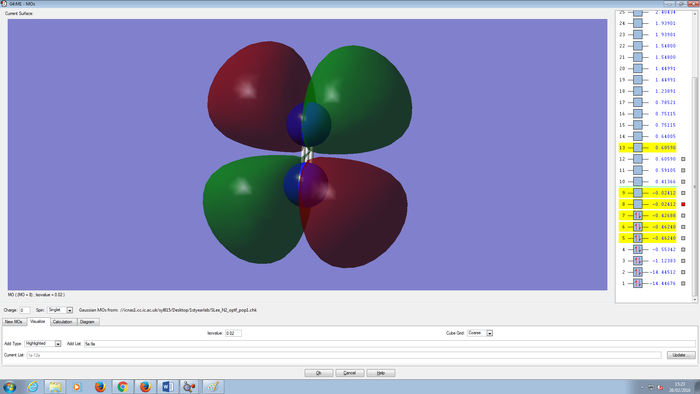
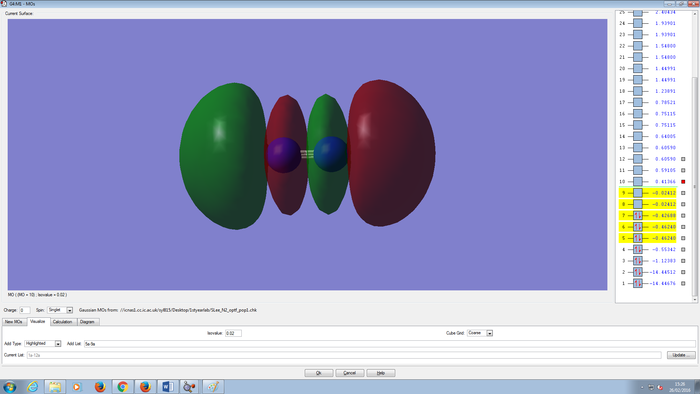
CH4 molecule
A computational analysis was performed on CH4 molecule with Gaussian calculation. 3 optimization steps were performed on the CH4 molecule, and the graph below illustrates the total energy and the RMS Gradient Norm of the CH4 molecule for each step.
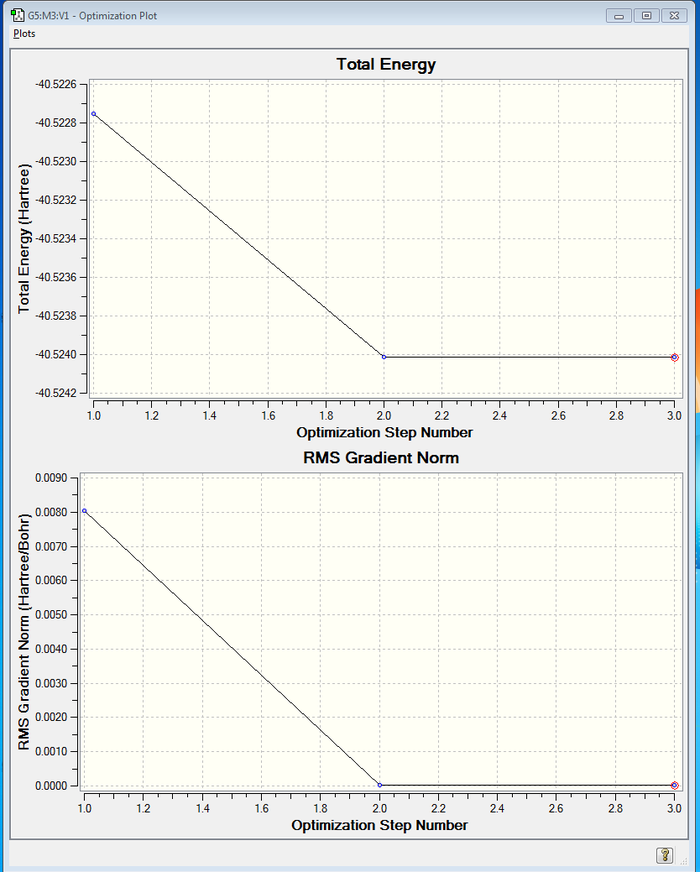
The following table presents the information upon the completion of optimization and frequency analysis.
| Structure | ||
|---|---|---|
| ||
| Information | ||
| Molecule | CH4 | |
| Calculation Method | RB3LYP | |
| Basis Set | 6-31G(d,p) | |
| Final Energy E(RB3LYP) (a.u.) | -40.52401404 | |
| RMS gradient (Hartree/Bohr) | 0.00003263 | |
| Point Group | TD | |
Completion of the Gaussian optimization process was ensured by checking with the Gaussian generated output data. The following table illustrates the results.
Item Value Threshold Converged?
Maximum Force 0.000063 0.000450 YES
RMS Force 0.000034 0.000300 YES
Maximum Displacement 0.000179 0.001800 YES
RMS Displacement 0.000095 0.001200 YES
Predicted change in Energy=-2.256043D-08
Optimization completed.
-- Stationary point found.
Since the values of the maximum force, RMS force, maximum displacement and RMS displacement were below their respective threshold values, it can be determined that for the optimized structure of CH4 molecule, the Gaussian calculation process was completed.
3D Structure
CH4 molecule |
Charge Distribution
Calculation of charge distribution of CH4 molecule was then performed following the optimization and frequency analysis. The diagram shows its charge distribution. The atoms are coloured according to the charge distribution.
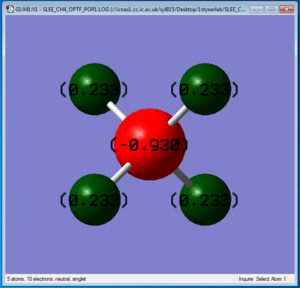
The charge of the Carbon atom found was -0.930, and each Hydrogen atom, +0.233, as calculated by Gaussian. This differed from the expected values of -4 for the Carbon atom and +1 for each Hydrogen atom. A possible reason could be because the expected values are calculated based on the classical model, where charges were assigned to each type of atom. However, the actual values yielded by the Gaussian calculations were performed using quantum mechanical calculations, such that the electron density for each atom was redistributed in order to obtain the most optimized structure of CH4.
Vibrational and IR Analysis
Vibrational and IR analysis was subsequently performed on the final optimized structure of CH4 molecule. The following diagram summarizes the results obtained after the analysis.
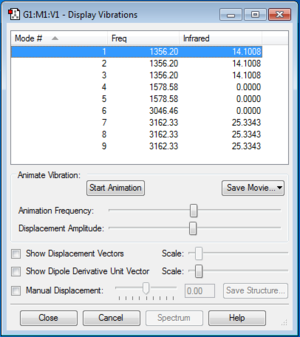
| How many modes do you expect from the 3N-6 rule? | 9 |
| Which modes are degenerate (i.e. have the same energy)? | Modes 1, 2 and 3 are degenerate. Modes 4 and 5 are degenerate. Modes 7, 8 and 9 are degenerate. |
| Which modes are "bending" vibrations and which are "bond stretch" vibrations? |
“Bond stretch” vibrations: modes 6, 7, 8 and 9 |
| “Bending” vibrations | modes 1, 2 and 3 |
| Which mode is highly symmetric? | Mode 6 |
| How many bands would you expect to see in an experimental spectrum of gaseous methane? | 2 |
The following diagram presents the computationally calculated IR spectrum data for CH4 molecule.
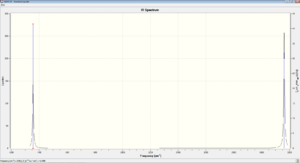
A prominent peak was observed for modes 1,2 and 3 which were indistinct on the IR Spectrum plot due to the similarities in frequency. Another prominent peak was observed for modes 7, 8 and 9, and similarly they could not be distinguished from each other due to the similarities in frequencies.
Molecular Orbitals Of CH4 molecule
| Description | Diagram |
|---|---|
| MO 1 It has an energy E=-10.16707. Since the energy level of this orbital is significantly lower than the energy levels of the rest of the MOs, it is likely that the electrons in this orbital are not involved in the bonding of the optimized CH4 molecule. Therefore, this is the 1s MO of the central Carbon atom, where the electrons occupying this orbital both belong to the Carbon atom. |
|
| MO 2 It has an energy E=-0.69041. The energy of this molecular orbital is slightly lower than MO 3, 4 and 5, but is significantly higher than the energy level of MO 1. It is therefore likely that the electrons in this orbital are involved in the C-H bond of the optimized CH4 atom. The 2s atomic orbital mixes with three 2p atomic orbitals to form 4 sp3 hybrid orbitals, with a bond angle of 109.47 degrees between each of the hybridised orbitals. However, this orbital is slightly lower in energy than that of MOs 3, 4 and 5, which is likely because this hybrid orbital has the greatest overlap with the 1s non-bonding orbital of Carbon and thus has the greatest degree of mixing, resulting in the lowering of energy of MO2. |
|
| MO 3 It has an energy E=-0.38831, and MOs 4 and 5 share the same energy level, with the only difference being the orientation of the MOs. The energy of this MO is slightly higher than energy level of MO2. The electrons in this orbital are involved in the C-H bond of the optimized CH4 molecule. Since the energy levels of MOs 3, 4 and 5 are similar, the MOs are degenerate, and therefore indicate that these orbitals are hybridised. This is the HOMO of the CH4 molecule. |
|
| MO 6 It has an energy E=+0.11824. The energy level of this MO is positive, and there is a green-coloured region within the large green region. Therefore, it is indicative that there is a 2p anti-bonding molecular orbital, as observed by the presence of nodes in the diagram. Since the energy value is slightly less positive than those of MOs 7, 8 and 9, it is likely that the anti-bonding orbital is contributed by the sp3 hybrid orbital which has the greatest degree of overlap with the 1s MO of Carbon and thus has the greatest degree of mixing, which slightly lowers the energy of this anti-bonding orbital. This is the LUMO of the CH4 molecule. |
|
| MO 7 It has an energy E=+0.17677, and MOs 8 and 9 also share the same energy level, with the only difference being the orientation of the MOs. The energy of this MO is slightly higher than energy level of MO2. Since the energy level of this MO is positive, the electrons are in the anti-bonding orbital are involved in the C-H bond of the optimized CH4 molecule, as observed by the nodes in the diagram. Since the energy levels of MOs 7, 8 and 9 are similar, the MOs are degenerate, and therefore indicate that these orbitals are hybridised. |
|
| MO 10 It has an energy E=+0.52915. This MO represents 3s orbital of the Carbon atom, as indicated by the more significant jump in energy level. |
|