Rep:Mod:Stassen14

The Cope Rearrangement Tutorial

In this experiment the Cope rearrangement of 1,5 hexadiene is studied. The cope rearrangment shown in figure 1 for this particular 1,5 hexadiene example indicates a pericyclic reaction in the form of a [3,3] sigmatropic shift.

Figure 1- Cope rearrangement of 1,5 hexadiene via [3,3] sigmatropic shift

The 1,5 hexadiene molecule has three rotating carbon-carbon bonds about the two middle Sp³ hybridized carbons, allowing it to take the form of various conformational isomers.

Previously the relative energies of the 1,5 hexadiene compound have been studied, using the DZP CCSD(T) method Rocque, Gonzales and Schaefer showed that the gauche(120)/anti/gauche(120) conformer is the lowest in energy . The possible Gauche and antiperiplanar molecules are created in Gaussian and optimized using various methods. It is known that the pericyclic reaction reacts via either the Boat or Chair transition structures shown in figure 2.

Figure 2- Chair (right) and Boat (left) transition structures

The relative energies of these transition structures are also explored at different levels of theory, and using different computational methods. The relative energies of the transition structures and starting conformers can then be compared to find activation energies and enthalpies for the various reactions.

Optimizing the Reactants and Products

Following the Tutorials instructions an APP conformer was drawn in Gaussian and optimized, followed by 2 Gauche conformer to discover that there was not a large difference in energy between the two sets of conformers.

Antiperiplanar and Gauche comparison

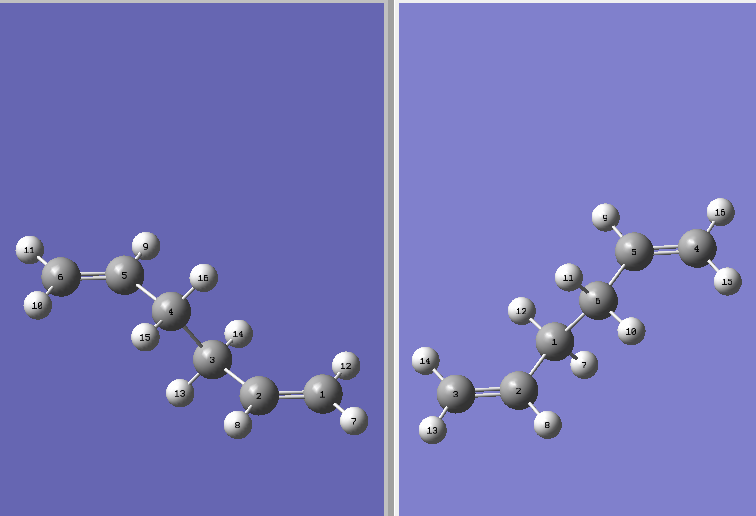
The antiperiplanar molecule shown in Figure 3 was drawn in gaussian (You have actually drawn the molecules in a program called GaussView, and then Gaussian performs the actual calculation. João (talk) 12:07, 27 December 2014 (UTC)) and optimized using the Hartree Fock 3-21G level to yield an energy of -231.68907 Hartree

The molecule shown below was symmetrized to a C2h point group (You should not symmetryze the molecule after optimization, as you are changing it's geometry and likely displacing it from the minimum. You can however use the point group editor to check what is the (approximate) point group of the molecule João (talk) 12:07, 27 December 2014 (UTC)).

Figure 3- An APP conformer with a dihedral angle of 180° between the middle four carbons and 0° between both the first and last four.

Next a Gauche structure shown in figure 4 was drawn and optimized. A resulting total energy of -231.69167 Hartree was found after the optimization at the HF/3-21G level.

The gauche molecule below was found to have a point group of c2

Figure 4- A Gauche conformer with a dihedral angle of -64° between the middle four carbons and 124° between both the first and last four.

The energy is much lower than expected (What were you expecting? Remember that the absolute value of the energy is not so relevant. João (talk) 12:07, 27 December 2014 (UTC)). It is even lower compared to the APP configuration, this is the opposite of what was expected. Furthermore the two values are very similar in energy.

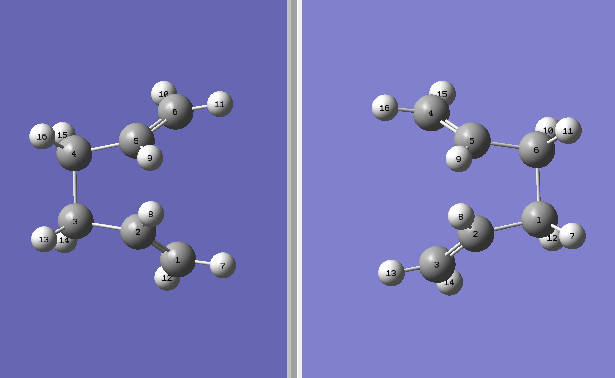
A different Gauche structure shown in Figure 5 was then drawn and optimized. This conformer was found to have an energy of -231.68772 Hartrees.

Figure 5- A Gauche conformer with a dihedral angle of 76° between the middle four carbons and 2° between both the first and last four carbons.

From the three results above it appears that even though they are very similar in energy the Gauche structure seems lower in energy. Other versions of the Gauche conformation and APP conformation will be drawn and optimized to obtain more information.

The table below shows and summarizes the result of the optimization of the 6 gauche conformers and 4 antiperiplanar conformers. They were all drawn using Gaussian and optimized using the Hartree fock 3-21G method to give the energies shown in the right hand column. The optimized structures were also symmetrized in the program to give the following point groups. It was hypothesized that the APP structures would be much lower in energy relative to the Gauche, particularly due to the increased steric hindrance that is expected. However it was found that the Gauche and APP conformers were of similar energy, and that the differences between conformers varied more than compared to whether they are in the Gauche category or APP. The Gauche3 structure shown in the table below was found to be the lowest in energy, where as another Gauche1 was found to be the highest energy according to the Hartree-fock 3-21G method. The results matched that of the appendix 1 given in the wiki.

Conformer	Structure	Point Group	Energy/Hartrees HF/3-21G
gauche1		C2	-231.68772
gauche2		C2	-231.69167
gauche3		C1	-231.69266
gauche4		C2	-231.69153
gauche5		C1	-231.68962
gauche6		C1	-231.68916
anti1		C2	-231.69260
anti2		Ci	-231.69254
anti3		C2h	-231.68907
anti4		C1	-231.69097

In contrary to the tutorials instructions it was found that the clean tool distorted bond angles significantly. It was much more effective to manually set bond angles and then optimizing this structure. A slight difference in bond angle of the input molecule generally caused a deviation in the energy of the optimized result.

Analysis of the Anti2 Conformation

The Ci anti2 conformation of 1,5-hexadiene was analyzed in particular. As can be seen from the previous table the conformer was of -231.69254 Hartree in energy and is of the Ci point group. Before optimization the dihedral APP angle was 180 between the four middle carbon centers, and 120 between the first four carbons on either side.

The bond angle between the first four carbons on either side was reduced to 114° after optimization. The dihedral angle of the middle four carbons centers remained at 180°.

The optimized structure of the anti2 conformer of 1,5-hexadiene at the HF/3-21G level was then re-optimized at the B3LYP/6-31G* level.

The energy was now found to be -234.559705u.a. This value is significantly higher than the previously generated value (It is actually lower, more negative. João (talk) 12:07, 27 December 2014 (UTC)). The symmetry of the molecule remained the same at Ci symmetry so the overall geometry has not changed much (Note that the symmetry can remain the same and the geometries still be rather different, think of an increase of the central bond by 6Å. João (talk) 12:07, 27 December 2014 (UTC)). The bond angle between the first four carbons on either side has now increased again from 115° to 119°.

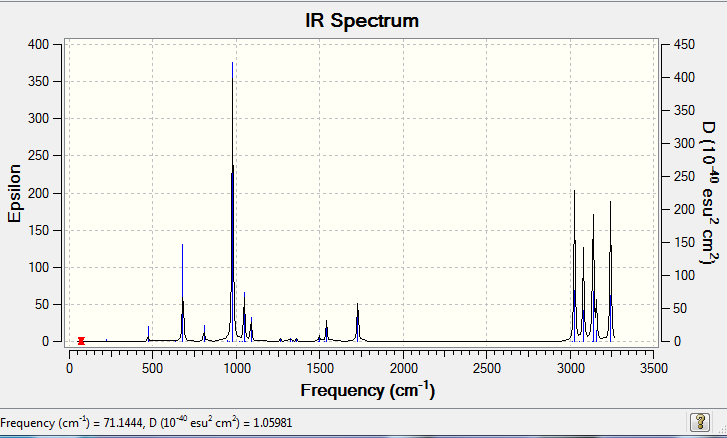
Next a frequency calculation was carried out starting from the optimized B3LYP/6-31G* structure. There were no imaginary frequency and the following IR spectrum was generated.

The spectra shows all the expected real frequency (What is the significance of the the frequencies being real? João (talk) 12:07, 27 December 2014 (UTC)) from the various carbon hydrogen stretches in the two Sp³ carbon centres as well as the 4 Sp² carbon centres.

Some therchemical data was also obtained from the calculation. The following table shows the potential energy at 0 K including the zero-point vibrational energy (E = Eelec + ZPE), energy at 298.15 K and 1 atm of pressure which includes contributions from the translational, rotational, and vibrational energy modes at this temperature (E = E + Evib + Erot + Etrans), additional correction for RT (H = E + RT) and the entropic contribution to the free energy (G = H - TS) from left to right.

Thermochemical Data in Hartree

Sum of electronic and zero-point Energies	Sum of electronic and thermal Energies	Sum of electronic and thermal Enthalpies	Sum of electronic and thermal Free Energies
-234.416255	-234.408963	-234.408019	-234.447872

Optimizing the "Chair" and "Boat" Transition Structures

In this section a transition structure optimization will be set up.

An allyl fragment (CH₂CHCH₂) was drawn and optimized using the HF/3-21G level of theory. The optimized structure is shown below.

The fragment had an energy of -115.82304u.a., and had a symmetry of the C2v point group.

Two identical fragments were positioned at 2.2A apart. This was then optimized using Hartree Fock at 3-21G level. The guess structure gave an optimized structure similar to the one showed in appendix 2. It can be seen below.

Figure 6- HF/3-21G level Optimized Chair transition structure

The optimized structure's transition bond lengths were significantly shorter at 2.02013 and 2.02016Å.

The vibrations were analyzed and an imaginary frequency was found at -818.02cm^-1 which corresponds to the cope rearrangement vibration(insert citation).

The transition structure was optimized again using the frozen coordinate method. This gave a very similar structure to the previous optimization of the same molecule.

The bond distances of the optimized structure were 2.200000 and 2.20003 Angstrom. This structure was then optimized again. the bonds were unfrozen and the force constants were not calculated (The force constants are actually calculated but only with respect to the forming bonds (by setting "Derivative" in mode redundant editor). This is necessary to find the negative curvature at the top of the barrier, otherwise how could the algorithm detect the transition state structure? João (talk) 12:07, 27 December 2014 (UTC)). The optimized result gave a structure where the transitions state bonds were 2.02077 and 2.02074. These bond lengths are slightly higher than when the previous method was used. The structure was of C2h symmetry and geometrically very similar to the optimized structure in part b).

Comparison of bond forming/bond breaking bond lengths in Å 

Computing force constants	redudant coordinate editor
2.02016	2.02077
2.02013	2.02074

The Boat transition structure was optimized using the QST2 method. The reactant and product anti2 structures where numbered as follows.

These two structures were then optimized to indicate the transition state via the QST2 method to give the following chair transition structure but more dissociated than normal.

Chair transition structure optimized using the QST2 method

The reactant and product geometries were then distorted to manually create a 0^o dihedral angle between middle four carbons, as well as a 100^o angle between the (C2-C3-C4) and (C5-C4-C3) in the reactant. The same was done for the products in an attempt to obtain the boat transition structure. The reactant and product are shown below.

This was optimized using QST2 to give the boat transition structure shown in the jmol file below. (How do you know this is a transition state structure? Did you check for the existence of a single imaginary frequency? João (talk) 12:07, 27 December 2014 (UTC))

Boat transition structure optimized using the QST2 method

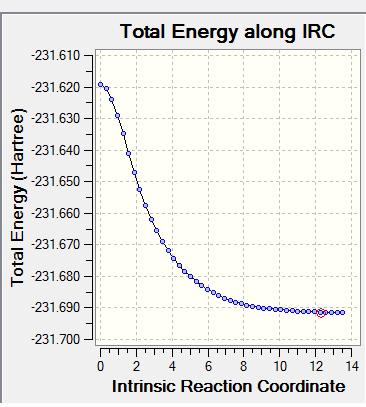
The optimized chair transition structure of -231.619322u.a. was then computed using the IRC Job type. Due to the symmetry of reaction it is only the forward direction is computed. The force constants were always calculated, and the number of points along the IRC was changed to 50 to get a more accurate curve. The IRC plot is shown below, from this it can be seen that it hasn't reached a minimum geometry yet.

The final point on the IRC curve gave a structure similar to Gauche2. The exact mirror image of the gauche2 image was computed, this means that this is the product of the gauche2 reactant. However it had the same energy as gauche4 at -231.69153u.a. The IRC was computed again but with 150 points instead of the previously set 50. The final point this time was at an energy of -231.69158, the energy has decreased slightly upon the addition of more points however it is still closer in energy to the gauche4 structure. The final points structure on the IRC curve with 100 points is shown below

The IRC was computed again but this time with recalculation of force constants at every point. This yielded the same energy of -231.69158u.a. and the same structure, a mirror image of gauche2. The structure generated had a dihedral angle of 67.19057 between the middle four carbons and, -118.83515 between the first four carbons on each side.

Now the activation energy of the reaction are calculated via both transition states. First the chair and the boat transition structure previously optimized in HF/3-21G are optimized at the B3LYP/6-31G* level of theory.

Comparison of B3LYP/6-31G* and HF/3-21G optimized structures

	Chair		Boat
	HF/3-21G	B3LYP/6-31G*	HF/3-21G	B3LYP/6-31G*
Energy	-231.619322	-234.505415	-231.602802	-234.49290
Structure
Point group	C2h	C2h	C2v	C2v
Transition bond lengths in Å	2.02077,2.02073	2.03828, 2.03721	2.14000, 2.13950	2.25536, 2.25536

The structures of both transitions states had the same point group at both levels of theory, however the bond length varied. It seemed that the Bond length for the higher lever of theory was much longer. Furthermore the energy varied as well. The B3LYP/6-31G* level of theory has a much lower energy. Compared to the values given in the appendix, it seemed that the HF/3-21G results were the same where as the B3LYP/6-31G* results were both around 0.05 higher. (Did you check an imaginary frequency was preserved after optimization? João (talk) 12:07, 27 December 2014 (UTC))

Anti2 was used to generate these two transition structures, so the energy levels from the anti2 structure optimized at each theory will be subtracted from the transition structures energy to find the activation energy in each. The findings are represented in the table below:

Thermodynamic information and Activation energies in (Hartree)

	Electronic energy		Sum of electronic and thermal energies at 298.15K		Sum of electronic and zero-point energies at 0K
	HF/3-21G	B3LYP/6-31G*	HF/3-21G	B3LYP/6-31G*	HF/3-21G	B3LYP/6-31G*
Anti2	-231.69254	-234.559705	-231.532566	-234.408963	-231.539540	-234.416255
Chair TS	-231.619322	-234.505415	-231.460807	-234.356755	-231.465985	-234.362683
Boat TS	-231.602802	-234.49290	-231.445300	-234.340285	-231.450928	-234.346080
ΔEChair	0.073218	0.05429	0.071759	0.052208	0.073555	0.053572
ΔEBoat	0.089738	0.066805	0.087266	0.068678	0.088612	0.070175

The activation energies are summarized in kcal/mol in the table below. comparing these results to the experimental values of 33.5 ± 0.5 kcal/mol via the chair transition structure and 44.7 ± 2.0 kcal/mol via the boat transition at 0K, it is clear that the B3LYP/6-31G* level of theory is much closer and even within the uncertainty range of the experimental values. Furthermore the results vary in comparison to the values given in the wiki, however the values obtained in this calculation are much closer to the experimental values at 0k. Especially the transition state for the boat at the higher B3LYP/6-31G* level. Hrovat D.A. has calculated a value of 33.2kcal/mol for the activation energy of Hexadiene also using the B3LYP/6-31G* calculations, and a Doering W.v.E. has experimentally found a value of 33.5±0.5 at 0K for the Chair activation energy.

Summary of Activation energies

	Sum of electronic and thermal energies at 298.15K		Sum of electronic and zero-point energies at 0K
	HF/3-21G	B3LYP/6-31G*	HF/3-21G	B3LYP/6-31G*
ΔEChair	45.03	32.76	46.16	33.62
ΔEBoat	54.76	43.10	55.60	44.04

The Diels Alder Cycloaddition

Cis Butadiene

Figure 7- HF/3-21G level Optimized cis butadiene with HOMO and LUMO visualized on the right and left respectively.

A cis Butadiene was drawn in gaussian and optimized at the HF 3-21G level to give an energy of -154.05394301 Hartree and a dihedral angle of -0.03180°. Figure 7 shows the visualized HOMO and LUMO orbitals. Both orbitals are asymmetric (With respect to which plane? Is there another plane of symmetry with respect to which the symmetry of the orbitals is distinct? João (talk) 12:07, 27 December 2014 (UTC)).

Ethylene + Cis butadiene Transition Structure

The transition structure for the [4+2] Diels Alder cycloaddition of cis butadiene and ehtylene was guessed and drawn in gaussian. The transition bonds were predicted to be around 2.2Å apart similarly to the previous pericyclic reaction. The structure was then optimized to a TS(berry) using the HF 3-21G level of theory to give the structure with a total energy of -231.60321 Hartree and symmetry of the Cs point group shown in figure 8.

Figure 8- HF/3-21G level Optimized transition structure of cis butadiene reacting with ehtylene in a [4+2] cycloaddition

The transition structure had transition bond lengths of 2.20913Å. According to Rowland and Taylor the Van der Waals radii of carbon atoms in a C-C bond is around 1.75Å , this shows that the bond has not yet formed in the transition structure that was guessed (But the bond distance is lower than twice the Van der Waals radius for carbor. Is that significant? João (talk) 12:07, 27 December 2014 (UTC)). The single bonds in cis butadiene part were shown to be 1.37007Å, and the double bond at 1.39450Å. The bond in ethylene was found to be 1.37588Å. Compared to ethylene's usual Sp² C-C bond length at 1.3305Å , the transition structure bond length is slightly higher as expected. Similarly, the butadienes single bond length was found to be 1.454Å and the two bonds at 1.338A by Craig et al. This is as expected, the length of the single bond has increased as it will have more sp² character, and at the same time the length of the two double bonds have decreased due to more sp³ character in the transition state structure.

Figure 9- The highest occupied molecular orbital visualized on the ethylene and butadiene transition state, showing that it is symmetrical

The HUMO and LUMO orbitals were visualized and shown in figures 9 and 10 respectively. Both the HOMO and LUMO orbitals were symmetrical.

Figure 10- The lowest unoccupied molecular orbital visualized on the ethylene and butadiene transition state, showing that it is symmetrical

The same transition structure guess was also optimization using the B3LYP/6-21G* level of theory to give the same structure and orbitals. However the energy was found to be -234.494549 Hartree. The structures bond lengths also varied compared to the other level of theory. With the transition bonds both at 2.26336Å, the ethylene bond at 1.39271Å, the previous double bonds in the butadiene at 1.38870Å, and the middle C-C bond in the butadiene at 1.40815Å. Similarly to the HF 3-21G optimization the bond lengths are expected to be in between the starting materials Sp³ and sp ² bond lengths. The transition structure also showed an imaginary frequency at 536.09cm^-1 which corresponds the concerted [4+2] addition, The figure below shows the this vibration.

The lowest positive frequency vibration at 140.27cm^-1 is shown in the figure below. This motion is asynchronous and shows the formation of two bonds at different times.

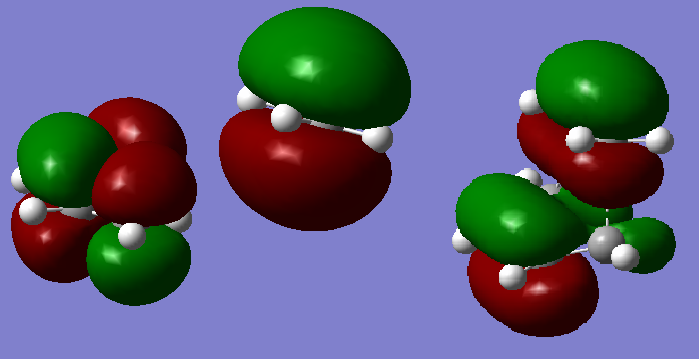
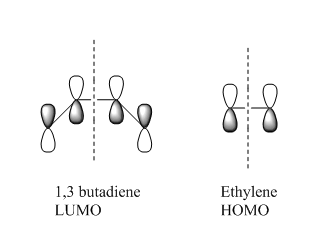
Due to time constraints the fragments of ethylene and 1,3 butadiene were optimized using the semi empirical AM1 method (You had all the orbitals you needed (except perhaps of ethene, which you know well) from previous calculations, why did you need this calculation here? It doesn't make much sense to compare orbitals at different levels of theory. João (talk) 12:07, 27 December 2014 (UTC)). This allowed for some orbital analysis. From the orbitals generated below it can be seen that the HOMO transition state orbital is formed from the LUMO of the 1,3 butadiene and the HOMO of the ethylene, both sets of π orbitals are symmetric and therefore are able to form the new MO as they have the same symmetry. (What about the transition state LUMO? João (talk) 12:07, 27 December 2014 (UTC))

The orbital diagram below shows the clearly that both orbitals involved in the creation of the HOMO of the transition state are symmetric about the axis of symmetry shown in the orbital diagram below, the left shows the LUMO of the 1,3 butadiene which corresponds to the left orbitals in the diagram above, and the right shows the HOMO of the ethylene which corresponds to the middle orbital diagram above.

(According to Woodward-Hoffmann rules whys is the reaction allowed? João (talk) 12:07, 27 December 2014 (UTC))

Cyclohexa-1,3-diene Reaction With Maleic Anhydride

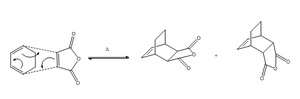
As a study of regioselectivity of the Diels Alder reaction, the two possible transition states in the cycloaddtion of cyclohexa--1,3 -diene with maleic anhydride are investigated. Figure 11 shows the reaction scheme of the [4+2] cyclo addition to give either the endo or exo forms.

Figure 11- Reaction scheme showing the exo product on the left and the endo product on the right

Similarly to the previous procedure, the two exo and endo transition states are guessed and drawn in gaussian. These were then optimized using the B3LYP/6-21G* level of theory to give the two transition states and their properties shown in the table below.

Two transition structures in the reaction of cyclohexa -1,3 -diene with maleic anhydride

Energies in Hartree, lengths in Å	Endo Transition State	Exo Transition State
Structure
Total Energy	-612.49548	-612.49100
Sum of electronic and zero-point energies at 0K	-612.314041	-612.30948
Sum of electronic and thermal energies at 298.15K	-612.303696	-612.29914
Point group	Cs	Cs
Transition bond lengths	2.26727, 2.26727	2.28975, 2.28944
Reaction vibration (click image to view)

From the table it can be noted that the endo transition state is slightly lower in energy, this means that endo will be the kinetic product, as its activation energy will be lower. The bond lengths in the endo transition state are also significantly lower compared to the exo transition state. This is thought to be due to the Secondary orbital interactions and steric effects.

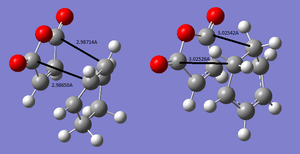
The main difference between the two transition states is that the exo in the exo, the maleic anhydride part of the transition state is closer to the Sp³ part of the cyclohexa -1,3 -diene. The endo transition state has the maleic anhydride part closer to the Sp² part of the maleic anhydride. The effects of this are investigated further. The inter-spacial distance between the carbons on the bridge and the carbons in the maleic anhydride are measured. This is more clearly illustrated in the image below where the lengths are given in Angstroms.

From this image in can be seen that these distances measure are shorter in the endo transition state. The exo could be higher in energy because it is more strained, the Sp³ carbons both possess a hydrogen that protrudes out of the plane, where as the sp² carbons have hydrogens in the same plane. According to Rowland et al, Van der Waals radii of carbon and hydrogen are 1.7 and 1.2 respectively. figure 12 shows that the distance between the carbon and the hydrogen is smaller than the combined radii of the Van der Waals forces, this indicates an unfavorable repulsive interaction. In the endo transition state these distances are 3.13806Å and 3.13882Å which is higher than the sum of Van der Waals radii.

Figure 12- showing the interspacial distance, that is less than the sum of Van der Waals radii, between the hydrogen and carbon in the exo transition state.

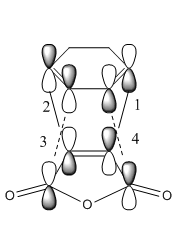
Secondary orbital interactions have been widely studied, it is thought that the interaction between the π orbitals of the Sp² in the endo transition state are able to have a favourable interaction with the π orbitals of the Sp² carbons in the maleic anhydride fragment. This is more clearly shown in the image below. Interactions 1 and 2 correspond to primary orbital interactions where the bond forms between the two reactants, secondary orbital interactions 3 and 4 show overlap of nearby orbitals of the same symmetry. The π orbitals are more clearly shown in the chemdraw image.

Orbital diagrams of reactants in the endo orientation experiencing possible secondary orbital overlap

Figure 13- This image shows the HOMO of the endo transition state, this orbital is likely formed from the two assymetric orbitals: HOMO of the Cyclohexa-1,3-diene and the LUMO of the maleic anhydride. It is clear that there are nodes between the carbons 3 and 4 and 1 and 2

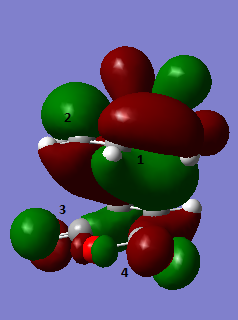
"A" refers to the HOMO of the Cyclohexa-1,3-diene and "B" refers to the LUMO of the maleic anhydride, as is clear both orbitals are asymmetric. The exo transition state is oriented so that the non bonding π orbitals of the Cyclohexa-1,3-diene are in close proximity to the sp³ carbon centers instead of the sp² hence there is no available symmetry matched π orbitals for any stabilizing interaction.

The HOMO of the transition state of the endo transition structure was examined for evidence of the secondary orbital interaction. Figure 13 shows image of the HOMO of the endo transition state optimized at the B3LYP/6-21G* level. There seems to be a node between the carbons 3 and 4 in the maleic anhydride and the carbons 1 and 2 in the Cyclohexa-1,3-diene. This could indicate that there is in fact no secondary orbital interaction in the transition state of the endo product (Perhaps there is something to be found for orbitals lower in energy than the HOMO? João (talk) 12:07, 27 December 2014 (UTC)). The fact that it is lower in energy could be fully due to steric hindrance factor explained earlier. Garcia et al, have shown that in the reaction with furan and maleic anhydride using MP/6-31G* that secondary charge transfer between the reactants does not take place, and concluded that the small endo preference is in fact due to dispersion forces. In this reaction cyclohexa -1,3 -diene is used instead of furan, however both reactants have a similar π orbital system. Given that no orbital overlap was shown between at the position where secondary orbital overlap is thought to occur in the HOMO of the endo transition structure, the energy and transition bond length differences between the endo and exo transition structures are likely to be caused by steric effects and repulsions.

References

.