Rep:Mod:Simulation of a Simple Liquid by Leo Hodges

Introduction to molecular dynamics simulation

Open the file HO.xls. In it, the velocity-Verlet algorithm is used to model the behaviour of a classical harmonic oscillator. Complete the three columns "ANALYTICAL", "ERROR", and "ENERGY": "ANALYTICAL" should contain the value of the classical solution for the position at time $t$, "ERROR" should contain the absolute difference between "ANALYTICAL" and the velocity-Verlet solution (i.e. ERROR should always be positive -- make sure you leave the half step rows blank!), and "ENERGY" should contain the total energy of the oscillator for the velocity-Verlet solution. Remember that the position of a classical harmonic oscillator is given by $x\left(t\right)=A\cos (\omega t+\varphi )$ (the values of $A$, $\omega$, and $\varphi$ are worked out for you in the sheet).

If,

$A=1,\omega =1$ and $\varphi =0$

Then the position using the analytical method is given by:

$x\left(t\right)=\cos (t)$

This is plotted below alongside the Velocity-Verlet, in order to show the comparison:

Figure 1: Position as a function of time using analytical and Velocity-Verlet methods

They are shown to be in very good agreement. The absolute error between the two methods, i.e. the difference between the two, is plotted below:

Figure 2: Difference between analytical and Velocity-Verlet methods

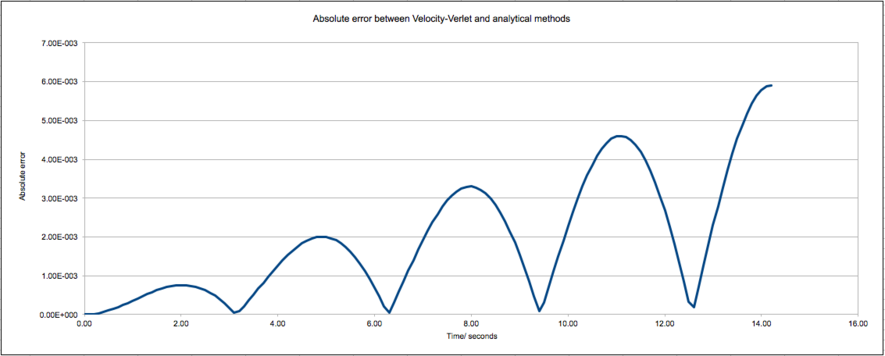
The error between the two methods is ultimately very small but is periodic and increases as total time elapsed increases.

The total energy is given by the sum of the potential and kinetic energies:

$E=\frac{1}{2}m{v}^2+\frac{1}{2}k{x}^2$

where $k=1,m=1$

Figure 3: Total energy as a function of time from the Velocity-Verlet method

The plot shows a wave oscillating around an average value, as expected for an ideal harmonic oscillator. The amplitude of oscillating is small and the total energy remains constant as there is no source of energy loss.

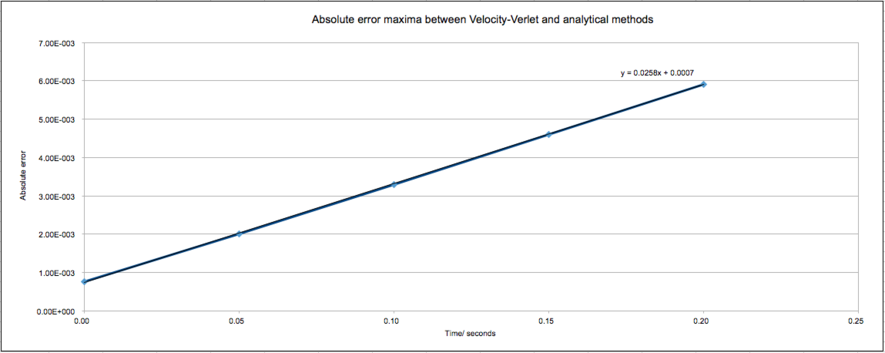
For the default timestep value, 0.1, estimate the positions of the maxima in the ERROR column as a function of time. Make a plot showing these values as a function of time, and fit an appropriate function to the data.

Figure 4: Linear correlation of error maxima

Experiment with different values of the timestep. What sort of a timestep do you need to use to ensure that the total energy does not change by more than 1% over the course of your "simulation"? Why do you think it is important to monitor the total energy of a physical system when modelling its behaviour numerically?'

The largest timestep that can be used, such that the amplitude of oscillation does not cause the energy to vary from the average by more than 1%, is 0.285.

Figure 5: Total energy as a function of time from the Velocity-Verlet method with 0.285 timestep

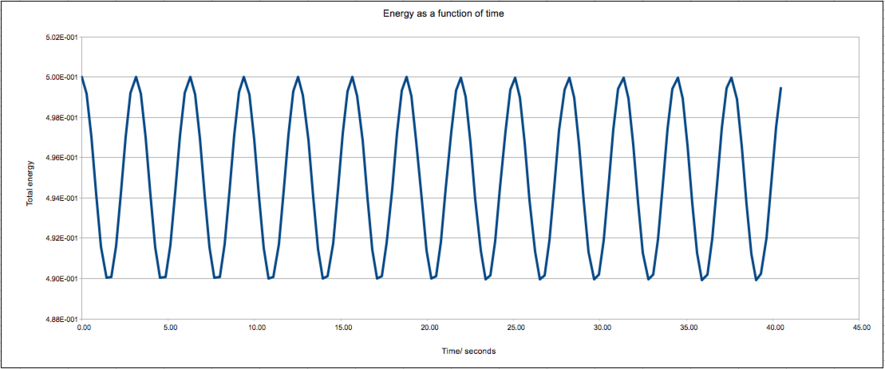
By monitoring the energy of a system, it can be shown that it is constant, as expected for a closed system.

For a single Lennard-Jones interaction, $\varphi \left(r\right)=4ϵ(\frac{{\sigma }^{12}}{r^{12}}-\frac{{\sigma }^6}{r^6})$, find the separation, $r_0$, at which the potential energy is zero. What is the force at this separation? Find the equilibrium separation, $r_{eq}$, and work out the well depth ($\varphi \left(r_{eq}\right)$). Evaluate the integrals $\underset{2\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi \left(r\right)\mathrm{d}r$, $\underset{2.5\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi \left(r\right)\mathrm{d}r$, and $\underset{3\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi \left(r\right)\mathrm{d}r$ when $\sigma =ϵ=1.0$.

$0=4ϵ(\frac{{\sigma }^{12}}{r^{12}}-\frac{{\sigma }^6}{r^6})$

$0=\frac{{\sigma }^{12}}{r^{12}}-\frac{{\sigma }^6}{r^6}$

$\frac{{\sigma }^{12}}{r^{12}}=\frac{{\sigma }^6}{r^6}$

$\frac{{\sigma }^{12}}{r^6}={\sigma }^6$

$\frac{{\sigma }^6}{r^6}=1$

$r^6={\sigma }^6$

$r_0=\sigma$

The force is given by:

$F=-\frac{d\varphi \left(r\right)}{dr}$

$F=-\frac{d\varphi \left(r\right)}{dr}=4ϵ(\frac{12{\sigma }^{12}}{r^{13}}-\frac{6{\sigma }^6}{r^7})$

As,

$r_0=\sigma$

Then,

$F=4ϵ(\frac{12{\sigma }^{12}}{{\sigma }^{13}}-\frac{6{\sigma }^6}{{\sigma }^7})$

$F=4ϵ(\frac{6}{\sigma })$

$F=\frac{24ϵ}{\sigma }$

The equilibrium separation, r_e, is the distance where $F=-\frac{d\varphi \left(r\right)}{dr}=0$.

$0=4ϵ(\frac{12{\sigma }^{12}}{r^{13}}-\frac{6{\sigma }^6}{r^7})$

$\frac{12{\sigma }^{12}}{{\sigma }^{13}}=\frac{6{\sigma }^6}{{\sigma }^7}$

$2{\sigma }^6=r^6$

$r_e=2^{\frac{1}{6}}\sigma$

This can then be substituted into the Lennard-Jones equation:

$\varphi \left(r\right)=4ϵ(\frac{{\sigma }^{12}}{2^2{\sigma }^{12}}-\frac{{\sigma }^6}{2{\sigma }^6})$

$\varphi \left(r\right)=4ϵ(\frac{1}{4}-\frac{1}{2})$

$\varphi \left(r\right)=-ϵ$

The integral of the Lennard-Jones potential is:

$\underset{2.5\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi \left(r\right)=4ϵ(\frac{{\sigma }^{12}}{r^{12}}-\frac{{\sigma }^6}{r^6})dr$

If $\sigma =ϵ=1$

$=4ϵ(\frac{{\sigma }^{12}}{11r^{11}}-\frac{{\sigma }^6}{5r^5}){|}_{2.5\sigma }^{\mathrm{\infty }}=-0.00818$

$=4ϵ(\frac{{\sigma }^{12}}{11r^{11}}-\frac{{\sigma }^6}{5r^5}){|}_{2\sigma }^{\mathrm{\infty }}=-0.0248$

$=4ϵ(\frac{{\sigma }^{12}}{11r^{11}}-\frac{{\sigma }^6}{5r^5}){|}_{3\sigma }^{\mathrm{\infty }}=-0.00329$

Estimate the number of water molecules in 1ml of water under standard conditions. Estimate the volume of 10000 water molecules under standard conditions.

The density of water at 298K is 0.997 g/cm³, therefore the mass of 1 mL of water is 0.997 g. The mass of a water molecule is 2.99 x 10^-23.

$$\begin{gathered} \frac{0.997}{2.99\times 10^{-23}}=3.33\times 10^{23} \\ molecules \end{gathered}$$

10,000 water molecules would weight 2.99 x 10^-19 and would occupy 2.99 x 10^-19 cm³

Consider an atom at position $(0.5,0.5,0.5)$ in a cubic simulation box which runs from $(0,0,0)$ to $(1,1,1)$. In a single timestep, it moves along the vector $(0.7,0.6,0.2)$. At what point does it end up, after the periodic boundary conditions have been applied?.

The atom would be at position $(0.2,0.1,0.7)$.

The Lennard-Jones parameters for argon are $$\begin{gathered} \sigma =0.34\mathrm{n}\mathrm{m},ϵ \\ / \\ {k}_B=120\mathrm{K} \end{gathered}$$. If the LJ cutoff is $r^{*}=3.2$, what is it in real units? What is the well depth in $$\begin{gathered} {\mathrm{k}\mathrm{J} \\ \mathrm{m}\mathrm{o}\mathrm{l}}^{-1} \end{gathered}$$? What is the reduced temperature $T^{*}=1.5$ in real units?

$r^{*}=\frac{r}{\sigma }$

Therefore,

$3.2\times 0.34=1.088nm$

The well depth is given by $ϵ=120K/cdot1.38\times 10^{-23}J{K}^{-1}=1.656\times 10^{-21}J$

And finally,

$T^{*}=\frac{k_{B}T}{ϵ}$

Therefore:

$\frac{1.5\times 1.656\times 10^{-21}}{1.38\times 10^{-23}}=180K$

Equilibration

Why do you think giving atoms random starting coordinates causes problems in simulations? Hint: what happens if two atoms happen to be generated close together?

If atoms are initially randomly positioned, it is possible that configurations are created where atoms are placed very close to one another. Such configurations may be physically impossible in reality and give extremely high Lennard-Jones potentials, causing problems and inaccuracies in simulations.

Satisfy yourself that this lattice spacing corresponds to a number density of lattice points of 0.8. Consider instead a face-centred cubic lattice with a lattice point number density of 1.2. What is the side length of the cubic unit cell?

Lattice spacing in x,y,z = 1.07722 1.07722 1.07722

A simple cubic unit cell has one lattice point, thus the volume occupied by a lattice point is equal to:

$$\begin{gathered} V=1.07722^3=1.25000 \\ unit{s}^3 \end{gathered}$$

Therefore the number density of lattice points is given by:

$\rho =\frac{1}{1.25000}=0.8$

A face centered unit cell contains four lattice points, so the length of the cubic unit cell with lattice number density of 1.2 is equal to:

$1.2=\frac{4}{L^3}$

$L=\sqrt[3]{\frac{4}{1.2}}=1.494$

Consider again the face-centred cubic lattice from the previous task. How many atoms would be created by the create_atoms command if you had defined that lattice instead?

Created orthogonal box = (0 0 0) to (10.7722 10.7722 10.7722)

The face centred cubic cell has a unit length of 1.494, so the created box will contain:

$$\begin{gathered} (\frac{10.7722}{1.494}{)}^3=374.85 \\ unit \\ cells \end{gathered}$$

A face centred cubic cell has 4 lattice points, thus the number of atoms created would be equal to:

$$\begin{gathered} 374.85\times 4=1500 \\ atoms \end{gathered}$$

Using the LAMMPS manual, find the purpose of the following commands in the input script:

mass 1 1.0
pair_style lj/cut 3.0
pair_coeff * * 1.0 1.0

The first row defines only one type of atom and that they all have mass 1.0. The second row, pair_style, calculates the Lennard-Jones potential between pairs of atoms. The command has a cutoff argument, setting global cutoffs for all pairs of atoms, i.e. the maximum distance for which the Lennard-Jones potential can be calculated. In this case it is 3.0 but it can be smaller or larger than the dimensions of the simulation box. The final row, pair_coeff, overrides the global cutoff command for a specific pair of atoms.

Figure 6: Velocity Verlet algorithm.

Given that we are specifying ${\mathbf{x}}_i\left(0\right)$ and ${\mathbf{v}}_i\left(0\right)$, which integration algorithm are we going to use?

The Velocity Verlet algorithm will be used as position and velocity are calculated at the same value of the time variable.

Look at the lines below.

### SPECIFY TIMESTEP ###
variable timestep equal 0.001
variable n_steps equal floor(100/${timestep})
variable n_steps equal floor(100/0.001)
timestep ${timestep}
timestep 0.001

### RUN SIMULATION ###
 run ${n_steps}
 run 100000

The second line (starting "variable timestep...") tells LAMMPS that if it encounters the text ${timestep} on a subsequent line, it should replace it by the value given. In this case, the value ${timestep} is always replaced by 0.001. In light of this, what do you think the purpose of these lines is? Why not just write:

timestep 0.001
run 100000

This set of code is such that no matter what you define the timestep to be, the same overall amount of time is run.

Make plots of the energy, temperature, and pressure, against time for the 0.001 timestep experiment (attach a picture to your report). Does the simulation reach equilibrium? How long does this take? When you have done this, make a single plot which shows the energy versus time for all of the timesteps (again, attach a picture to your report). Choosing a timestep is a balancing act: the shorter the timestep, the more accurately the results of your simulation will reflect the physical reality; short timesteps, however, mean that the same number of simulation steps cover a shorter amount of actual time, and this is very unhelpful if the process you want to study requires observation over a long time. Of the five timesteps that you used, which is the largest to give acceptable results? Which one of the five is a particularly bad choice? Why?

Figure 7: Plots of time against energy, temperature and pressure for the 0.001 timestep

If only the first second is plotted, it can be seen that the system reaches equilibrium in about 0.3 seconds:

Figure 8: One second plots of time against energy, temperature and pressure for the 0.001 timestep

A plot of time versus energy for timesteps from 0.001 to 0.015 helps us choose the most appropriate timestep:

Figure 9: Plot of time against energy for varying timesteps

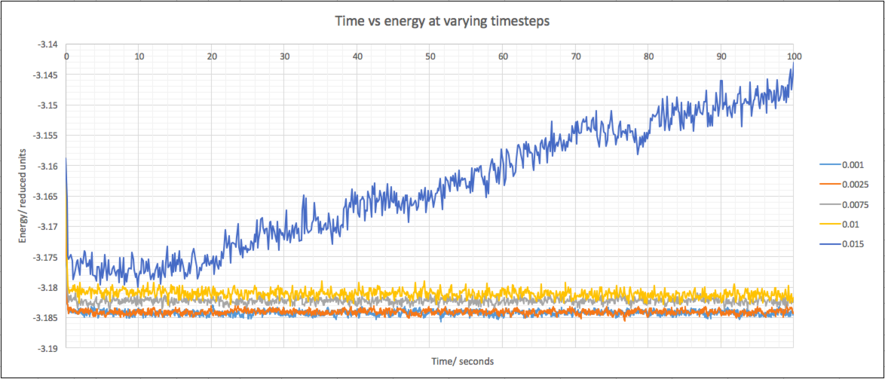
The 0.015 timestep is clearly a bad choice because the system does not equilibrate and the energy gradually increases. The other timesteps all equilibrate and all look similar. A plot of the first second will differentiate between the remaining timesteps:

Figure 10: One second plot of time against energy for varying timesteps

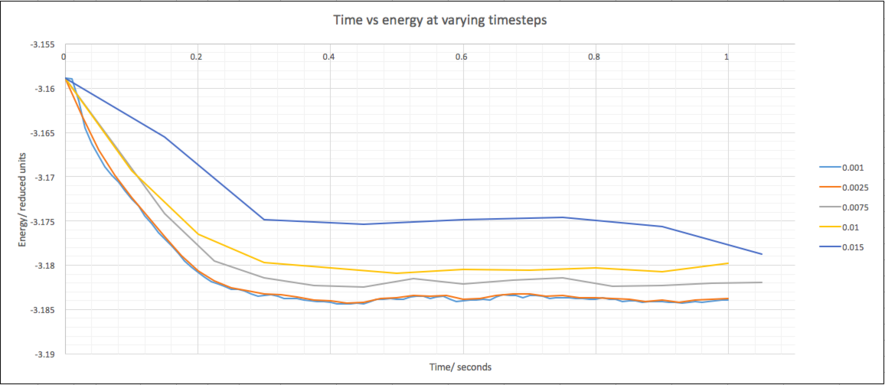
0.01 is the largest timestep that equilibrates, however, 0.0025 appears to be a good choice because it matches the 0.001 timestep very closely, the smallest timestep but does not take as much time or oscillate as much.

Running simulations under specific conditions

Choose 5 temperatures (above the critical temperature $T^{*}=1.5$), and two pressures (you can get a good idea of what a reasonable pressure is in Lennard-Jones units by looking at the average pressure of your simulations from the last section). This gives ten phase points — five temperatures at each pressure. Create 10 copies of npt.in, and modify each to run a simulation at one of your chosen $(p,T)$ points. You should be able to use the results of the previous section to choose a timestep. Submit these ten jobs to the HPC portal. While you wait for them to finish, you should read the next section.

The chosen temperatures were T = 1.5, 2.0, 2.5, 3.0 and 6.0 at pressures p = 2.5 and 3.0. These simulations are to be performed with a 0.0025 timestep, owing to the previous conclusion.

We need to choose $\gamma$ so that the temperature is correct $T=\mathfrak{𝔗}$ if we multiply every velocity $\gamma$. We can write two equations:

$\frac{1}{2}\sum _i{m}_i{v}_i^2=\frac{3}{2}N{k}_{B}T$

$\frac{1}{2}\sum _i{m}_i{\left(\gamma v_i\right)}^2=\frac{3}{2}N{k}_B\mathfrak{𝔗}$

Solve these to determine $\gamma$.

Equating the equations gives us:

$\frac{\frac{1}{2}\sum _i{m}_i{\left(\gamma v_i\right)}^2}{\frac{1}{2}\sum _i{m}_i{v}_i^2}=\frac{\frac{3}{2}N{k}_B\mathfrak{𝔗}}{\frac{3}{2}N{k}_{B}T}$

So,

${\gamma }^2=\frac{\mathfrak{𝔗}}{T}$

Therefore:

$\gamma =\sqrt{\frac{\mathfrak{𝔗}}{T}}$

Use the manual page to find out the importance of the three numbers 100 1000 100000. How often will values of the temperature, etc., be sampled for the average? How many measurements contribute to the average? Looking to the following line, how much time will you simulate?

### MEASURE SYSTEM STATE ###
thermo_style custom step etotal temp press density
variable dens equal density
variable dens2 equal density*density
variable temp equal temp
variable temp2 equal temp*temp
variable press equal press
variable press2 equal press*press
fix aves all ave/time 100 1000 100000 v_dens v_temp v_press v_dens2 v_temp2 v_press2
run 100000

The penultimate line of code, starting fix aves, takes the defined inputs, such as density and pressure and averages them every set number of timesteps. How it does this is dictated by the numbers given in the line of code. These numbers represent Nevery, Nrepeat and Nfreq respectively. The Nevery number is after every however many timesteps an input value is taken, in this case 100. Nrepeat is how many times the input values are used for calculating averages, 1000, and Nfreq calculates an average every this many timesteps, 100000 for this code.

An average is taken every 100000 timesteps and an input value is taken every 100 timesteps, so 1000 measurements will contribute to the average. With a timestep of 0.0025 and 100000 timesteps to be run, 250 seconds will be simulated overall.

When your simulations have finished, download the log files as before. At the end of the log file, LAMMPS will output the values and errors for the pressure, temperature, and density $\left(\frac{N}{V}\right)$. Use software of your choice to plot the density as a function of temperature for both of the pressures that you simulated. Your graph(s) should include error bars in both the x and y directions. You should also include a line corresponding to the density predicted by the ideal gas law at that pressure. Is your simulated density lower or higher? Justify this. Does the discrepancy increase or decrease with pressure?

Figure 11: Density as a function of temperature plot

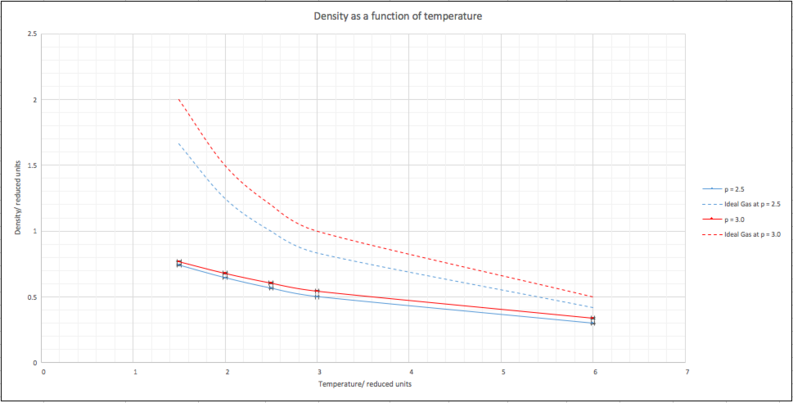
The plot for the simulated density as a function of temperature of the liquid at different pressures follow very similar curves. As expected, the higher pressure gives a higher density along the curve. Error bars are included on both axes but are small; to the order of around 10^-2 for density. The curves for the liquid at both pressures are lower than their respective ideal gas equivalent. This can be rationalised due to the fact that an ideal gas is considered to have no significant particle-particle interactions, while the liquid simulation takes into account Lennard-Jones interactions, so particles are more likely to be found further apart from one another. The discrepancy can be seen to increase with pressure, this fits with the conclusion.

As temperature increases, the liquid and ideal gas curves converge, however. As the temperature increases, thermal kinetic energy overrides the intermolecular interaction effects and the liquid becomes more like an ideal gas.

Calculating heat capacities using statistical physics

As in the last section, you need to run simulations at ten phase points. In this section, we will be in density-temperature $({\rho }^{*},T^{*})$ phase space, rather than pressure-temperature phase space. The two densities required at $0.2$ and $0.8$, and the temperature range is $2.0,2.2,2.4,2.6,2.8$. Plot $C_V/V$ as a function of temperature, where $V$ is the volume of the simulation cell, for both of your densities (on the same graph). Is the trend the one you would expect? Attach an example of one of your input scripts to your report.

Many quantities in statistical thermodynamics can be calculated by considering how far the system is able to fluctuate from its average equilibrium state. For example, if the temperature is held "constant", then we know that the total energy must be fluctuating. The magnitude of these fluctuations actually tell us about the heat capacity of the system, according to the equation

$C_V=\frac{\partial E}{\partial T}=\frac{\mathrm{V}\mathrm{a}\mathrm{r}\left[E\right]}{k_B{T}^2}=N^2\frac{⟨E^2⟩-{⟨E⟩}^2}{k_B{T}^2}$

$\mathrm{V}\mathrm{a}\mathrm{r}\left[E\right]$ is the variance in $E$, $N$ is the number of atoms, and it is a standard result from statistics that $\mathrm{V}\mathrm{a}\mathrm{r}\left[X\right]=⟨X^2⟩-{⟨X⟩}^2$. The $N^2$ is required because LAMMPS divides all energy output by the number of particles (so when you measure $E$, you are actually measuring $E/N$).

The script used to perform the simulation for density 0.8 and temperature 2.0 is shown below:

### DEFINE SIMULATION BOX GEOMETRY ###
variable d equal 0.8
lattice sc ${d}
region box block 0 15 0 15 0 15
create_box 1 box
create_atoms 1 box

### DEFINE PHYSICAL PROPERTIES OF ATOMS ###
mass 1 1.0
pair_style lj/cut/opt 3.0
pair_coeff 1 1 1.0 1.0
neighbor 2.0 bin

### SPECIFY THE REQUIRED THERMODYNAMIC STATE ###
variable T equal 2.0
variable timestep equal 0.0025

### ASSIGN ATOMIC VELOCITIES ###
velocity all create ${T} 12345 dist gaussian rot yes mom yes

### SPECIFY ENSEMBLE ###
timestep ${timestep}
fix nve all nve

### THERMODYNAMIC OUTPUT CONTROL ###
thermo_style custom time etotal temp press
thermo 10

### RECORD TRAJECTORY ###
dump traj all custom 1000 output-1 id x y z

### SPECIFY TIMESTEP ###

### RUN SIMULATION TO MELT CRYSTAL ###
run 10000
unfix nve
reset_timestep 0

### BRING SYSTEM TO REQUIRED STATE ###
variable tdamp equal ${timestep}*100
fix nvt all nvt temp ${T} ${T} ${tdamp}
run 10000
reset_timestep 0

### MEASURE SYSTEM STATE ###
unfix nvt
fix nve all nve
thermo_style custom step etotal temp
variable e equal etotal
variable e2 equal etotal*etotal
variable temp equal temp
fix aves all ave/time 100 1000 100000 v_temp v_e v_e2
run 100000

variable avetemp equal f_aves[1]
variable avetemp2 equal f_aves[1]*f_aves[1]
variable avgesquare equal f_aves[3]
variable squareavge equal f_aves[2]*f_aves[2]
variable shola equal ${avgesquare}-${squareavge}
variable Cv equal atoms*atoms*${shola}/${avetemp2}
variable vol equal vol
variable CvV equal ${Cv}/${vol}

print "Temperature: ${avetemp}"
print "Cv: ${Cv}"
print "Cv/V: ${CvV}"

The data from the ten simulations could then be plotted on the same graph in Excel:

Figure 12: Cv/V as a function of temperature plot

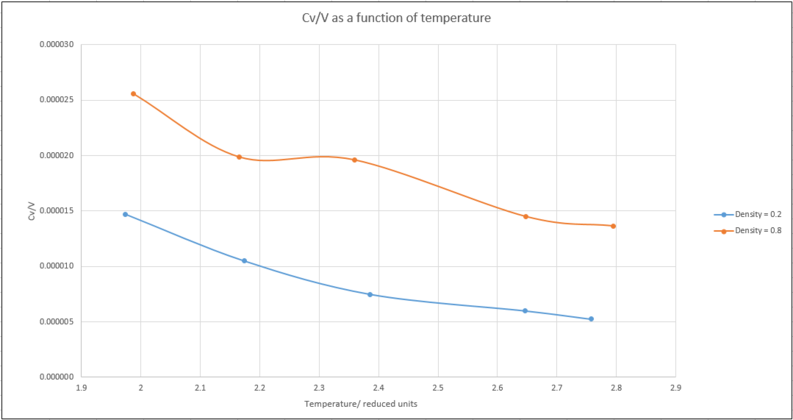
The heat capacity of the system can be seen to decrease as the temperature increases for both densities. This is an observation that can be rationalised by quantum mechanics. As the temperature increases, higher energy levels start to populate and consequently reduce the ability of the system to absorb further energy. This reduces the heat capacity.

As for the difference between the trends for the two densities, the higher heat capacity for the greater density is also to be expected. A greater number of particles in an equivalent volume would be able to absorb more energy than a system with a lower density.

Structural properties and the radial distribution function

Figure 13: Coexistence curve for the Lennard-Jones system (temperatures and densities in reduced units)

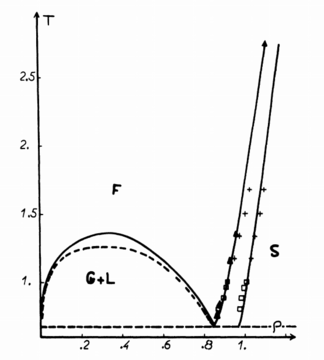
Perform simulations of the Lennard-Jones system in the three phases. When each is complete, download the trajectory and calculate

$g(r)$

and

$\int g(r)\mathrm{d}r$

. Plot the RDFs for the three systems on the same axes, and attach a copy to your report. Discuss qualitatively the differences between the three RDFs, and what this tells you about the structure of the system in each phase. In the solid case, illustrate which lattice sites the first three peaks correspond to. What is the lattice spacing? What is the coordination number for each of the first three peaks?

The density and temperature parameters for the three phases were chosen based on the phase diagram shown in Figure 13. The density of the gas, liquid and solid were 0.05, 0.8 and 1.2 respectively, while the temperature for all the phases was 1.2.

Figure 14: Radial Distribution Function for three phases (left) and solid (right)

Figure 15: Face centred cubic unit cell

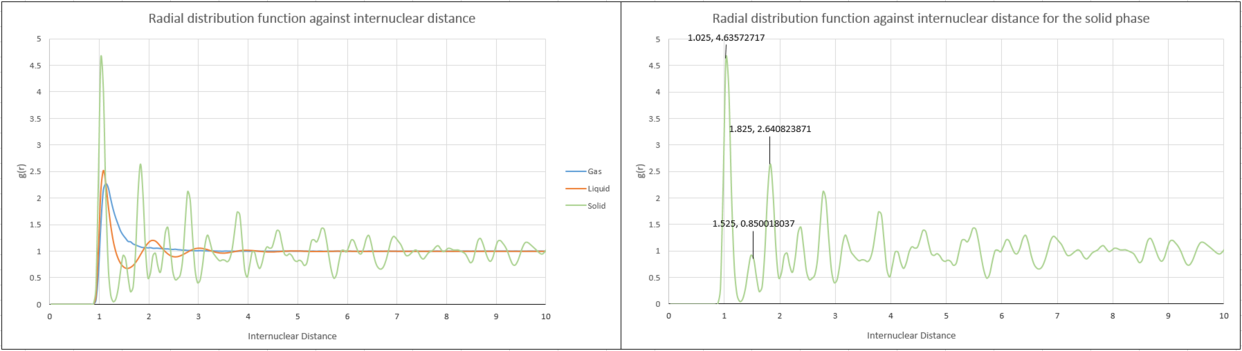
The radial distribution function describes how the density in a system of particles varies as a function of distance from a reference particle, in this case a randomly chosen atom. Essentially, it is the probability of finding a particle at a certain distance away from the reference particle, relative to an ideal gas.

The densities of the solid and the liquid are similar, so the separation of molecules would be expected to be similar. This is the case but the fundamental difference between the two phases is the presence of long-range order in the solid state that is not seen in the liquid state. Three peaks can be seen for the liquid phase at low internuclear distances before the amplitude diminishes to 1. The short range order observed, despite the constant motion of particles in a liquid can be explained by coordination shells. The distances between the randomly chosen particle and the particles in the first coordination shell is much shorter than for the second coordination shell, which in turn is shorter than the third until there is essentially no coordination, hence the amplitude of 1.

For the face centred cubic solid state, however, the first three peaks are found at similar internuclear distances as that of the liquid but the amplitude does not diminish to the same extent and the peaks are more clearly defined than in the liquid. This is because in a solid, the atoms are in fixed positions and can be defined consistently regardless of the reference particle.

In the case of the gas there is only one peak due to very little 'local structure'. At distances shorter than the atomic diameter, g(r) is zero due to strong repulsive forces.

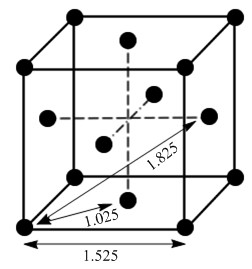
Due to the fixed nature of atoms in the face centred cubic lattice, the internuclear distance of the peaks, as shown in Figure 14, can be used to find the lattice spacing. Figure 15 shows the internuclear distances the peaks correspond to, in the context of a face centred cubic unit cell.

Dynamical properties and the diffusion coefficient

In the D subfolder, there is a file liq.in that will run a simulation at specified density and temperature to calculate the mean squared displacement and velocity autocorrelation function of your system. Run one of these simulations for a vapour, liquid, and solid. You have also been given some simulated data from much larger systems (approximately one million atoms). You will need these files later.

As before, the density of the vapour is 0.05, the liquid is 0.8 and the solid 1.2.

Make a plot for each of your simulations (solid, liquid, and gas), showing the mean squared displacement (the "total" MSD) as a function of timestep. Are these as you would expect? Estimate $D$ in each case. Be careful with the units! Repeat this procedure for the MSD data that you were given from the one million atom simulations.

$D=\frac{1}{6}\frac{\partial ⟨r^2\left(t\right)⟩}{\partial t}$

Figure 16: Mean square displacement for the vapour phase

Ultimately, all of the phases show a linear correlation between the mean square displacement and the number of timesteps. In the case of the vapour phase, this is after an initial 1500 timesteps of non-linearity. This allows us to use the gradient of the slope in the equation shown above to estimate the diffusion coefficient, D. As the differential is with respect to time, t, we must divide the gradient by the length of the timestep, 0.002. With a gradient of 0.0374, we obtain for the diffusion coefficient:

$D=\frac{1}{6}\frac{0.0374}{0.002}=3.11$

For 1 million atoms, we obtain a very similar coefficient:

$D=\frac{1}{6}\frac{0.037}{0.002}=3.08$

Figure 17: Mean square displacement for the liquid phase

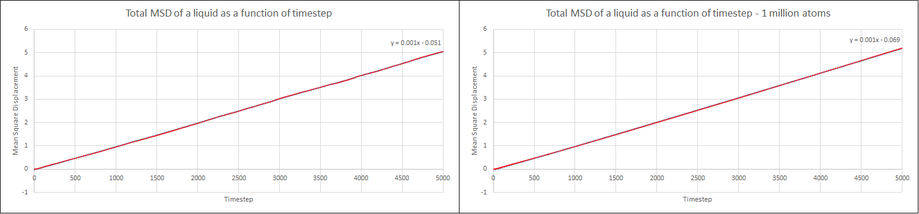
The liquid phase has a very close linear trend from the very first timestep. It also exhibits a much smaller overall mean square displacement at the final timestep compared to the vapour, thus also a smaller gradient. The value for the coefficient is calculated to be:

$D=\frac{1}{6}\frac{0.001}{0.002}=0.083$

The same diffusion coefficient is obtained for 1 million atoms as the gradient of the slope is the same.

Figure 18: Mean square displacement for the solid phase

Finally, the solid phase shows linearity after around 250 timesteps but in this case the gradient is very close to zero. A very small overall mean square displacement is to be expected for a face centred cubic lattice with fixed atoms. The diffusion coefficient is calculated to be:

$D=\frac{1}{6}\cdot \frac{1\times 10^{-8}}{0.002}=8.3\times 10^{-7}$

For 1 million atoms:

$D=\frac{1}{6}\cdot \frac{1\times 10^{-8}}{0.002}=8.3\times 10^{-6}$

It can also be seen that throughout the calculations of the three phases, simulating one million atoms provided very little benefit and is unnecessary. The only noticeable difference being the smoother gradient in the mean square displacement plot for the solid phase.

We can also calculate the diffusion coefficient using the velocity autocorrelation function, which we denote by

$C\left(\tau \right)=⟨\mathbf{v}\left(t\right)\cdot \mathbf{v}(t+\tau )⟩$

In essence, this function tells us how different the velocity of an atom will be at time $t+\tau$ to its velocity at time $t$. At long times, we expect $C\left(\mathrm{\infty }\right)=0$, because the velocities of atoms should become uncorrelated at very long times. By this, we mean that the velocity of an atom at a particular time should not depend on its velocity a long time in the past — the exact form of $C\left(\tau \right)$ tells us how long "a long time" is. Remarkably, we can calculate the diffusion coefficient by integrating this function:

$D=\frac{1}{3}\underset{0}{\overset{\mathrm{\infty }}{\int }}\mathrm{d}\tau ⟨\mathbf{v}\left(0\right)\cdot \mathbf{v}\left(\tau \right)⟩$

The "optional output-3" file from your simulations contains measurements of the VACF. The format of the files is similar to the format of the MSD data files: the first column contains the timestep at which the VACF data was evaluated (this is $\tau$, in timestep units), the next three contain $C\left(\tau \right)$ for the Cartesian components of the velocity, and the final column contains the VACF for the whole velocity.

In the theoretical section at the beginning, the equation for the evolution of the position of a 1D harmonic oscillator as a function of time was given. Using this, evaluate the normalised velocity autocorrelation function for a 1D harmonic oscillator (it is analytic!):

$C\left(\tau \right)=\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}v\left(t\right)v(t+\tau )\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{v}^2\left(t\right)\mathrm{d}t}$

Be sure to show your working in your writeup. On the same graph, with x range 0 to 500, plot $C\left(\tau \right)$ with $\omega =1/2\pi$ and the VACFs from your liquid and solid simulations. What do the minima in the VACFs for the liquid and solid system represent? Discuss the origin of the differences between the liquid and solid VACFs. The harmonic oscillator VACF is very different to the Lennard Jones solid and liquid. Why is this? Attach a copy of your plot to your writeup.

The positiion of a classical harmonic oscillator is given by:

$x(t)=A\cos (\omega t+\varphi )$

If

$t=t+\tau$

Then,

$x(t)=A\cos (\omega (t+\tau )+\varphi )$

This can be differentiated with respect to t, using the chain rule, to give us the velocity as:

$\frac{dx(t)}{dt}=v(t)=-A\omega \sin (\omega (t+\tau )+\varphi )$

This can be substituted into:

$C\left(\tau \right)=\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}v\left(t\right)v(t+\tau )\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{v}^2\left(t\right)\mathrm{d}t}$

To give:

$C\left(\tau \right)=\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\sin (\omega t+\varphi )\sin (\omega (t+\tau )+\varphi )dt}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{\sin }^2(\omega t+\varphi )dt}$

We can use the trigonometric identity:

$sin(u+v)=sin(u)cos(v)+cos(u)sin(v)$

To give:

$C\left(\tau \right)=\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\sin (\omega t+\varphi )[\sin (\omega t+\varphi )\cos (\omega \tau )+\cos (\omega t+\varphi )\sin (\omega \tau )]dt}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{\sin }^2(\omega t+\varphi )dt}$

$C\left(\tau \right)=\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\sin (\omega t+\varphi )\sin (\omega \tau )\cos (\omega t+\varphi )+{\sin }^{}(\omega t+\varphi )\cos (\omega \tau )dt}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{\sin }^2(\omega t+\varphi )dt}$

$C\left(\tau \right)=\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\sin (\omega t+\varphi )\sin (\omega \tau )\cos (\omega t+\varphi )dt}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{\sin }^2(\omega t+\varphi )dt}+\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{\sin }^2(\omega t+\varphi )\cos (\omega \tau )dt}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{\sin }^2(\omega t+\varphi )dt}$

$C\left(\tau \right)=\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\sin (\omega t+\varphi )\sin (\omega \tau )\cos (\omega t+\varphi )dt}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{\sin }^2(\omega t+\varphi )dt}+\cos (\omega \tau )$

$C\left(\tau \right)=\frac{\sin (\omega \tau )\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\sin (\omega t+\varphi )\cos (\omega t+\varphi )dt}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{\sin }^2(\omega t+\varphi )dt}+\cos (\omega \tau )$

The bottom integral does not converge but the top integral is a combination of an even and an odd function, therefore as long as the limits are equal and opposite, the integral will tend to zero.

$\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\sin (\omega t+\varphi )\cos (\omega t+\varphi )dt=0$

Therefore:

$C\left(\tau \right)=\cos (\omega \tau )$

Figure 19: Velocity autocorrelation function for the solid and liquid phases and the harmonic oscillator

The minima on the plots represent collisions with other atoms. The solid plot shows a decaying nature after the initial collision on the solid plot due to its high degree of order, while the liquid exhibits only one minima. This represents a collision with the solvent cage. There are no collisions in the case of the harmonic oscillator, so the amplitude of the periodic wave remains constant.

Use the trapezium rule to approximate the integral under the velocity autocorrelation function for the solid, liquid, and gas, and use these values to estimate $D$ in each case. You should make a plot of the running integral in each case. Are they as you expect? Repeat this procedure for the VACF data that you were given from the one million atom simulations. What do you think is the largest source of error in your estimates of D from the VACF?

A running integral of the VACF can be approximated using the trapezium rule, allowing us the estimate the diffusion coefficient with the below equation:

$D=\frac{1}{6}\cdot \frac{1\times 10^{-8}}{0.002}=8.3\times 10^{-6}$

Figure 20: Running integral of the velocity autocorrelation function for the vapour phase

The diffusion coefficient works out to be 3.294 and for the 1 million atom system, 3.268. This is similar to the result obtained above from the mean square displacement method.

Figure 21: Running integral of the velocity autocorrelation function for the liquid phase

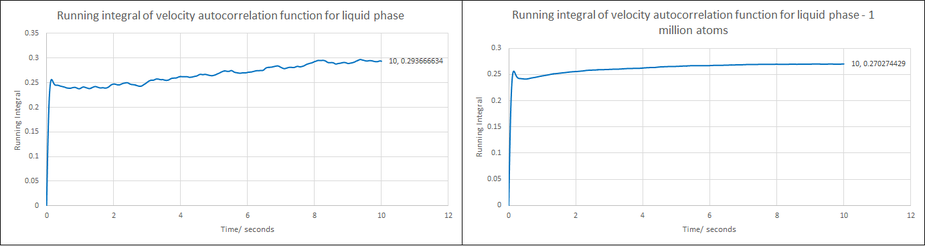
A value of 0.0977 is obtained for the liquid phase diffusion coefficient and 0.09 for the equivalent 1 million atom system, which is again similar to the previous method.

Figure 22: Running integral of the velocity autocorrelation function for the solid phase

The diffusion coefficient for the solid is again essentially zero which is to be expected. A value of 1.84 x 10^-4 is calculated for the diffusion coefficient and 4.53 x 10^-5 for the 1 million atom system. It can again be seen that there is little difference in the result from the 1 million atom simulation and it is therefore unnecessary to simulate such a large number of atoms. More accurate estimations of the diffusion coefficient could be obtained by using more sophisticated methods of approximating the integral.