Rep:Mod:Shadow
This report lays out the results from computational calculations into MgO crystal structure. Using computational methods the free energy and lattice parameters of MgO crystals where modeled at different conditions and from this the thermal expansion constant was determined.
Introduction
Structure
 |
 |
Crystal structures can be simplified down to a infinitely repeating unit cell. This unit cell is defined by vectors a,b and c. The unit cell can be defined as anything as long as when it is infinitely repeated in all 3 directions it forms the crystal structure. There is 2 main types of unit cells. The conventional unit cell and the primitive unit cell. The conventional unit cell is defined as the smallest cell that has basis vectors that defines an right handed axial setting and the edges of the cell is along the symmetry directions of the crystal lattice[1], the conventional cell for MgO, shown in figure 1, has a face centered cubic structure. The primitive cell is a cell that only consists of one lattice point[2] and is the simplest unit cell that can be defined for a structure, the primitive cell for MgO is shown in Image 2 and has a body centered structure.
Theory
Just as photons are quantised unit of electromagnetic waves, phonons are quantised units of vibrational waves. They arise from the oscillating vibrations of the atoms within a crystal structure. Phonons are one of the two main elementary participles in solids along with electrons and has a great effect on the physical properties of the solid. [3]. Phonons are the physical origin of thermal expansion, as the energy increases the system gets more vibrational energy and the atoms vibrate more and with a larger amplitude causing them to move away from each other and increasing the equilibrium bond distance between them.
The density of states is a measurement of the amount of vibrational states in a certain energy interval i.e how many phonons there are that has the same vibrational frequency. The computer program used calculated the phonons at different points in the crystal 3D structure based on how it was set up. For each point 6, 3 orbitals from each atom mix giving 6 orbitals overall, phonon energy values was calculated. The density of states graph is then just simply a graph of how often each frequency shows up. The more points are used in the calculation the more comparable the results will be with the actual structure.
| Symmetry points | (u,v,w) | [kx,ky,kz] |
|---|---|---|
| W | (,,) | [,, 0] |
| L | (,,) | [,,] |
| Γ | (0,0,0) | [0,0,0] |
| X | (0,,) | [0,,0) |
| W | (,,) | [,, 0] |
| K | (,,) | [,,0] |
The phonons is not equally distributed through the structure and will be different based on where in the lattice they are taken. It will be impossible to calculate the phonons for every single K value in the structure so when doing phonon distribution calculations only certain points are taken and these points are know as symmetry points. These symmetry points are chosen to represent the structure and from them a general view of what the phonon distribution is can be found. These points are defined by a vector (uvw). When this vector is applied to the function for k, one point in the latice gets defined by 3 different k values (kx,ky,kz) The table to the right shows the symmetry points that was used here.
When doing the density of stated calculations a certain shrinking factor of the form X*Y*Z has to be applied to the structure. This shrinking factor determines the amount of point at which the calculations will be done. What the shrinking factor does is it divides the x, y and z axis into X, Y and Z pieces respectively. The points at which the calculations are done is taken at the center of the cubes that is generated by the division of the axis. Only half of the cubes are sampled as rest is equal by symmetry.
Program
The program DL visualize uses GULP (General Utility Lattice Program) to calculate the properties of the system. GULP uses algorithms, that uses analytical first and second derivatives, for the symmetry-adapted energy minimization of solids.[4]
Calculations
Buckingham repulsive potential force field interactions
MgO internal Energy
Using GULP the energy per unit cell was calculated. The Mg ion is given a charge of +2e and the O ion a charge of -2e where e is the elementary charge. The calculation was done using a force field to describe the interactions between the atoms. The calculation resulted in a total lattice energy of -41.075 eV per unit cell (-3963.14 kJ/mol of unit cells). This is for a primitive unit cell of one Mg and one O with cell parameters a=b=c=2.9783 Å and internal angles α=β=γ=600. The cell had a volume of 18.68 Å3 at 0K and 0GPa
Phonon and DOS Calculations

The phonon distribution was calculated at 50 different points along the k space path W-L-Γ-X-W-K.
Each of these letters represents a certain symetry point in the latice and relates to a certain value of k as shown in the introduction.
The output from the program had all the lines in one colour making it hard too see where a single line went. The data was replotted using excel making it easier to see the different lines, and just better looking in general. The phonon dispersion can be seen in Image 1 above.
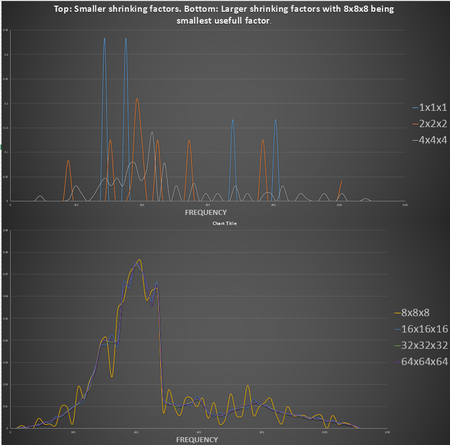
As mentioned before the density of states is the amount of times a ceratain frequency appears in the phonon calculations. The density of states graphs is shown on the left for shrinking factors 1x1x1,2x2x2, 4x4x4, 8x8x8, 16x16x16, 32x32x32 and 64x64x64. The higher the shrinking factor goes the more k points are used to calculate the density of states, from just 1 point at 1x1x1, which is kx=ky=kz=0.5, to 131072 points at 64x64x64.
Although it is not necesary to run calculations at 64x64x64, as can be seen from the graph there isn't much difference in the graphs from 8x8x8 and 64x64x64. At 64x64x64 it is just a bit more smoothed out but the general shape of the graph stays the same and thus 8x8x8 is the minimum grid size that gives a reasonable approximation of the DOS. Below 8x8x8 the graphs aren't a good representation as they generally consists of distinct peaks which is an unrealistic representation as the crystal has continues energy bands and not individual levels, as can be seen on the dispersion curve. 8x8x8 would be suitable for calculations on structures that has similar symetry to MgO such as CaO. It might not be suitable for calculations on structures that has a larger repeat unit such as a zeolite structure that is more complex than MgO so would require sampling over a larger range. For a more simple structure like a metal it would work but would be larger than the minimum realistic representation.
Harmonic approximation
| Shrinking Factor | Free Energy (eV) | Change from previous |
|---|---|---|
| 1x1x1 | -40.930301 | |
| 2x2x2 | -40.926609 | 0.003692 |
| 3x3x3 | -40.926432 | 0.000177 |
| 4x4x4 | -40.92645 | -1.8E-05 |
| 8x8x8 | -40.926478 | -2.8E-05 |
| 16x16x16 | -40.926482 | -4E-06 |
| 32x32x32 | -40.926483 | -1E-06 |
The best way of running calculations is to do it over a infinite grid of k-points. This will take way too much time so finding the smallest k-space grid that still gives accurate results is important. To do this the change in free energy is assessed over various grid sizes as shown in the table. The energy increases from 1x1x1 to 2x2x2 and then again to a maximum at 3x3x3 and then decreases from there too 32x32x32. 3x3x3 is the first accurate to both 1 meV and 0.5 meV and 4x4x4 is the first accurate to 0.1 meV. 8x8x8 was taken to do the next set of calculations as it still decreased by a relatively large amount from 4x4x4 and going to 16x16x16 doesn't decrease the free energy by much so must have started converging already.
Thermal Expansion

The thermal expansion constant is defined as: Rearanging and integrating gives Thus the thermal expansion constant \alpha_v is equal to the gradient of a graph of lnV against T. As seen on the top part of image 5 the graph is not perfectly linear. The calculations were done from 0K to 1000K and for a trend line done over all points the value for R^2 is 0.969, not too far off the desired value but doing it just from 300K to a 1000K gives a R^2 value of 0.997, a lot better. Can then also take the trend line for 100K to 300K, which has a R^2 value of 0.969 aswell. This then gives 3 different values for over three temperature ranges.

Over the full range it is 2.345x10^-5 K^-1 for 300K to 1000K it is 2.786x10^-5 K^-1 and for 100K to 300K it is 1.372x10^-5 K^-1. Some literature values where: in the range of 77-1315K a value of 3.57X10^-5 K-1 [5] And values between 0.22x10^-5 and 1.52x10^-5 K^-1 for a range of 100K - 1100K [6]. They are all of the same order of magnitude and there isn't too much difference between the calculated and reference values.
The Helmholtz free energy where also calculated at these temperatures and the graph is shown in image 6. It can be seen that the free energy increases , absolute value goes down, as temperature increases. This is because the equation for Helmholtz free energy is A=U-TS. The free energy stays constant and thus as temperature increases the free energy will go up.
Molecular Dynamics

The conventional unit cell consists of 2 irreducible atoms and the cell used to do the molecular dynamics calculations on consisted of a 2x2x2 grid of conventional cells giving it 64 irreducible atoms. Thus when the volume generated by the calculations is divided by their numbers it produces the volume per formula unit for each type of calculation, and allows them to be compared. The results is shown in Image 7.
The MD calculation resulted in a αv of 2.787x10-5 with an R2 value of 0.998. Thus the MD calculations is a lot more accurate than the quasi-harmonic calculations. The difference is due to MD being a better calculation to use and that it takes into account the change in internal energy of the system and atomic interactions.
The MD calculations where done on a 2x2x2 super cell instead of a 8x8x8 one like the rest of the calculations. This is due to it being a more complex calculation to run and going from 2x2x2 to 8x8x8 is a 64 times increase in atoms and a lot larger increase in complexity.
At higher temperatures the cell volume should go up drastically when it crosses the melting point and then again when it crosses the boiling point as the crystal structure will looses any long range symmetry in both these cases. MD should be better at predicting where these points are
Conclusion
The thermal expansion for MgO has been calculated and shown that it differs at temperatures close to room temperature than at higher temperature.
Refrences
- ↑ Conventional Cell - Online Dictionary Of Crystallography". Reference.iucr.org. N.p., 2016. Web. 10 Mar. 2016. http://reference.iucr.org/dictionary/Conventional_cell
- ↑ Primitive Cell - Online Dictionary Of Crystallography". Reference.iucr.org. N.p., 2016. Web. 10 Mar. 2016. http://reference.iucr.org/dictionary/Primitive_cell
- ↑ "phonon". Encyclopædia Britannica. Encyclopædia Britannica Online. Encyclopædia Britannica Inc., 2016. Web. 10 Mar. 2016 <http://www.britannica.com/science/phonon>.
- ↑ Julian D. Gale J. Chem. Soc., Faraday Trans., 1997,93, 629-637,DOI:10.1039/A606455H
- ↑ Smyth, J. R., S. D. Jacobsen, and R. M. Hazen. "Comparative Crystal Chemistry Of Dense Oxide Minerals". Reviews in Mineralogy and Geochemistry 41.1 (2000): 157-186. Web. 10 Mar. 2016.
- ↑ Thermal Expansion 2.3.5". Kayelaby.npl.co.uk. N.p., 2016. Web. 10 Mar. 2016
