Rep:Mod:Sh1226

Introduction

Transition states of various reactions and their corresponding reaction mechanisms were studied using computer software GaussView in this computational experiment. Three reactions under investigation were Cope rearrangement of 1,5-hexadiene, Diels Alder cycloaddition between cis-butadiene and ethene as well as between cyclohexa-1,3-diene and maleic anhydride.

The three calculation theory levels used were DFT/B3LYP/6-31G*, HF/3-21G and semi-empirical/AM1, in the order of increasing approximation. Semi-empirical (e.g AM1) theory level solves Schrodinger equation without considering any electron-electron interations – it is an approximation to the Hartree Fock (e.g. 3-21G) theory level which takes in account of average electron-electron repulsion. However, B3LYP/6-31G* is the most accurate method out of the three since it not only includes terms that appear in Hartree Focks calculation, i.e. kinetic energy of electrons, electron-nuclei interactions and coulombic interactions between electron clouds, it also takes in account of exchange correlation potential due to spin and charge. Therefore, calculations done on semi-empirical AM1 theory in this experiment is most approximate while DFT/B3LYP/6-31G* gives the more accurate result.

Nf710 (talk) 12:10, 4 November 2015 (UTC)Good understanding of the theory here. Could possible say how HF is more computational expensive as it solves the many electron wavefunction through slater determinants, where DFT uses functionals of the electron density which is less expensive but still very accurate.

The Cope Rearrangement

Figure 1: Cope Rearrangement of 1,5-hexadiene

Cope rearrangement of 1,5-hexadiene is an example of [3,3]-sigmatropic rearrangement and the reaction mechanism is illustrated in Figure 1. It occurs via a concerted reaction mechanism in which a chair or boat transition state is formed. The boat transition state is known to locate at a higher energy level in comparison to the chair transition state since its structure experiences a greater strain. Different transition states have potential to form energetically distinct conformers. There are ten of such conformers, either in an anti-periplanar conformation or a gauche conformation [1].

1,5-hexadiene with an "anti" linkage and a gauche" linkage

1,5-hexadiene with an anti-periplanar and a gauche conformation were drawn, cleaned and optimised separately using the HF/3-21G theory level. After symmetrising the optimised structure, it was found that the optimised anti conformer has C2 symmetry and energy of -231.69260235 Hartrees whereas the optimised gauche conformer has C1 symmetry and energy of -231.69266121 Hartrees.

Due to the presence of the three free rotating C-C bond, there are many possibilities for the structures of 1,5-hexadiene. Conformer in the gauche form was thought to experience a greater steric repulsion between the relatively large HC=CH2 groups, known as 1,3-diaxial interaction. In gauche form, HC=CH2 groups are closer to each other (60°) than in the anti-periplanar conformation, where two HC=CH2 groups locate 180° apart. This greater steric clash between HC=CH2 groups present in gauche form would raise its energy, making it thermodynamically less stable. Conformers with C=C double bond cis to each other would also experience unfavourable repulsion between the vinyl hydrogen, raising the energy of conformers. Therefore, the one predicted with the lowest energy would have C=C double bond trans to each other in an anti-periplanar conformation where the large R group, in this case CH=CH2 groups, would locate furthest apart from each other. This predicted structure was drawn and optimised using HF/3-21G theory level in order to calculate its conformation energy.


Figure 2: Conformation of 1,5-hexadiene predicted with high energy due to steric repulsion between the two relatively large R groups, HC=CH2	Figure 3: Conformation of 1,5-hexadiene predicted with the lowest energy since two large R groups, HC=CH2, are far apart, reducing steric effect and lowering the energy

However, the calculations done on the predicted structure turns out to have a higher energy than the gauche conformer with C1 symmetry created at start of this experiment. This contradicts with the idea that the greater steric repulsion between the large R group in gauche form leads to a higher energy. The reason for this could be due to the attractive interaction between the π orbital of C=C bond and the vinyl proton in such conformation, lowering its energy [1]. This gauche structure is known as the conformer with the lowest energy, as literature report indicated. [1]

Nf710 (talk) 12:04, 4 November 2015 (UTC)Very nice use of the new projections to show the steric clashing, you have clear researched literature and applied it to this problem. You could have perhaps gone into some more detail about the secondary orbital interactions. Perhaps even shown how the MOs from the gauche 3 state show secondary orbital interactions from the MOS developed in the .chk file this would have proved your theory.

Nf710 (talk) 12:07, 4 November 2015 (UTC)Your energies and point groups are correct. However you have compared bond lengths but not angles and dihedrals.

Conformation of 1,5-hexadiene

Structure

Energy at HF/3-21G theory level / Hartrees

Symmetry

Newman Projection

Anti-periplanar

-231.69260235

C2

Gauche

-231.69266121

C1

Predicted structure with the lowest energy, anti-periplanar

-231.69253529

Ci

Predicted 1,5-hexadiene conformation above has symmetry of Ci. This HF/3-21G optimised structure was then optimised at B3LYP/6-31G* level.

Methods of calculation

Structure

Energy / Hartrees

C1-C4 distance

C4-C6 distance

C6-C9 distance

HF/3-21G

-231.69253529

1.31616

1.50889

1.55287

B3LYP/6-31G*

-234.61171166

1.33350

1.50420

1.54816

When higher theory method was applied to optimise 1,5-hexadiene with Ci symmetry, the geometry changed slightly. C1-C4 bond distance increases but C4-C5 and C5-C9 bond distances decrease. However, the change is not significant enough for higher level of theory to be run. Higher level of calculation theory is often expensive and should be run on a more complicated molecule to obtain more accurate data.

Frequency calculation was then carried out on B3LYP/6-31G* optimised structure using the same calculation method.

It is found that 1,5-hexadiene with Ci symmetry has been optimised to minimum since all frequencies are real and positive.

Nf710 (talk) 12:14, 4 November 2015 (UTC)good frequency analysis, when we term frequency analysis we arnt that bothered about the peaks in the IR, they are all generated as functions from a localised group theory calculation we are just checking to see we have a local minimum and not a TS.

Thermochemistry-related data have also been calculated during the process:

Energetic Values	B3LYP/6-31G*
Sum of Electronic and Zero-point Energies at 0 K	-234.469215
Sum of Electronic and Thermal Energies at 298.15 K	-234.461866
Sum of Electronic and Thermal Enthalpies	-234.460922
Sum of Electronic and Thermal Free Energies	-234.500800

Sum of Electronic and Zero-point Energies refers to potential energy at temperature of 0K, including the zero-point energy. Sum of electronic and thermal energies is measured at 298.15K and 1 atm of pressure. Energies included consists all forms of kinetic energy: translational , rotational and vibrational energy. Sum of electronic and thermal enthalpies is measured based on RT (H=E+RT) correction and sum of electronic and thermal free energies includes the entropic contribution to the free energy G=H-TS.

Nf710 (talk) 12:17, 4 November 2015 (UTC) good understanding of the energies and they are correct

Optimizing the "Chair" and "Boat" Transition Structures

"Chair" Transition Structure

In order to characterise chair transition structure, allyl fragment CH2CHCH2 was created and optimised at the HF/3-21G level of theory. Two of these optimised allyl fragments were put together with their terminal ends being 2.2 Å apart, to model the guessed chair transition structure of 1,5-hexadiene. The guessed structure was then optimised in two different ways.

The first method used was TS(Berny) opt+freq, with an additional keyword opt=noeigen and force constants being calculated 'Once'. This directly optimises the guessed chair transition structure to transition state.

The second method using Redundant Co-ordinate Editor first froze reaction coordinate of the guessed chair transition structure (freezing bond to be formed between terminal allyl fragments) and then minimised the rest of the molecule to minimum. This optimised structure was optimised again but to transition state, after unfreezing their reaction coordinates. However, TS(Berny) method used this time does not involve the calculation of force constant.

Both of these two method calculations were ran on HF/3-21G theory level and results are illustrated below:

Methods of optimisation at HF/3-21G

Geometry

Energy / Hartrees

Negative vibration frequency/cm^-1

Vibrational frequency spectrum

Vibrational frequency animation

TS(Berny) opt + freq

-231.61932232

-817.94

Optimisation using Redundant Co-ordinate Editor

-231.61932220

-817.93

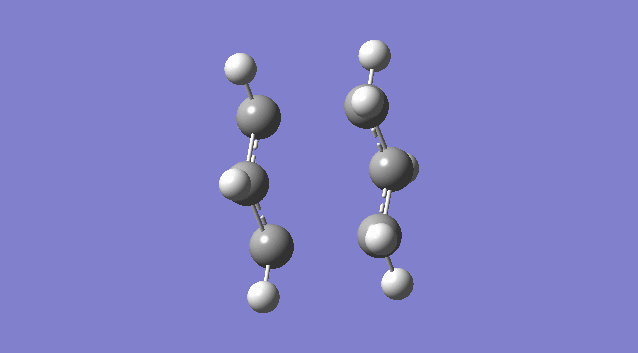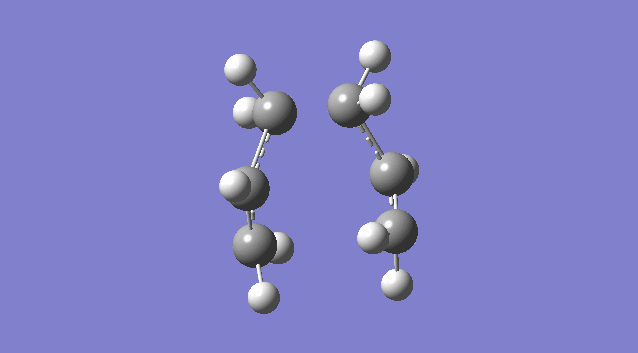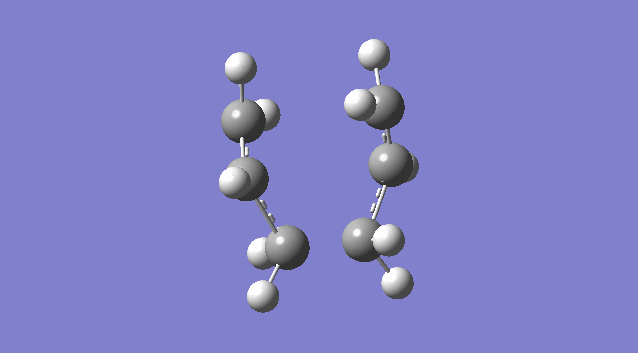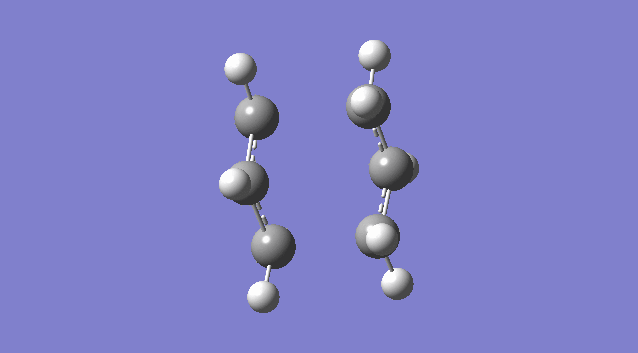Despite methods used to optimise chair transition structure are different, the results are very similar since the same guessed chair transition geometry was being minimised in both cases. Only one imaginary frequency is found in each case. The presence of one imaginary negative frequency means the corresponding structure has reached its saddle point, the maximum of the reaction trajectory, confirming the formation of transition state. The vibration at the negative frequency demonstrates the concerted nature of reaction: as two terminal atoms move toward each other at one end, the other two terminal carbon atoms move away from each other at the other end, simulating formation and breakage of bonds between terminal carbon atoms in Cope reaction.

Nf710 (talk) 12:22, 4 November 2015 (UTC) correctly optimised however it isn't a negative frequency its is an imaginary frequency that comes from a second derivative of the energy at that minimum to give the force constant which is then put into the eqution for a molecular oclisiltor. which has a term (k/m)^1/2 which give an imaginary number as you root a negative.

"Boat" Transition Structure

Boat transition structure is characterised using QST2 method. In this method, reactant 1,5-hexadiene (Ci symmetry) and product 1-5 hexadiene (Ci symmetry) were both built in Gaussview. The atoms in each structure were labelled to ensure the bonds break and form between the correct atoms. TS(QST2) opt+freq calculation was then set up on HF/3-21G theory level. However, this calculation failed in its first attempt and produced a dissociated chair transition state instead of a boat structure. This is because the starting reactant and product resemble the chair geometry rather than the boat.

Hence to solve this issue, dihedral angle between the central four carbon atoms (C2-C3-C4-C5) in both molecule was changed to 0° and inside C-C-C angle (C2-C3-C4 and C3-C4-C5) was set to 100°. This modified both reactant and product geometry to become more boat-like. QST2 calculation was repeated and the boat transition structure was successfully modelled.

Attempt

Input

Output

Energy/Hartrees

Negative frequency vibration/^-1

Vibrational frequency animation

1st

n/a

2nd

-231.60280223

-840.22

In comparison to chair structure, boat structure has a less negative energy value. This means it is at a higher energy level, raising activation energy required for Cope rearrangement of 1,5-hexadiene and making reaction pathway through boat transition state unfavorable.

Nf710 (talk) 12:29, 4 November 2015 (UTC) well documented and some understanding how frequency relates to energy, but I dont think you have grasped that it is an imaginary frequency and where it comes from like I explained in my previous comment.

Intrinsic Reaction Coordinate

Intrinsic Reaction Coordinate, IRC, is applied to the chair transition structure optimised using TS(Berny) method. IRC takes small geometry steps along the reaction pathway where the gradient of potential energy surface is the steepest from the transition state to the reactant and product. Since the starting reactant and product of cope rearrangement of 1,5-hexadiene is the same, IRC is only applied in the forward direction. Force was always calculated and 50 steps were used in the calculation.

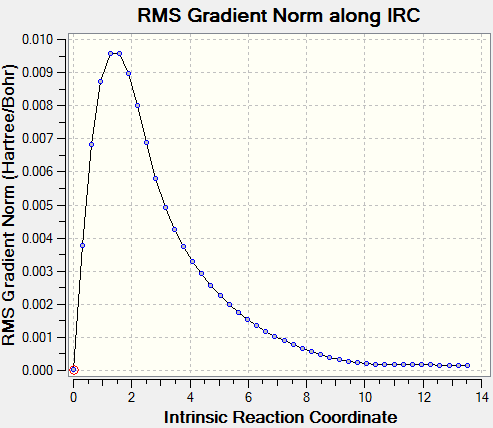
Figure 5: graph of gradient along IRC of chair transition state

Transition state locates at maximum point of potential energy surface, known as saddle point, where gradient of potential energy surface equals to zero. Both reactant and product are found at local minimum of potential energy surface where gradient of potential energy surface is also zero. IRC follows the steepest reaction pathway from transition state to reactant/product and the graph of gradient of potential energy surface along IRC starts and returns to zero, confirming the formation of transition state that lead to both reactant and product.

	HF/3-21G			B3LYP/6-31G(d)
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.619322	-231.466700	-231.461343	-234.556931	-234.414910	-234.408982
Boat TS	-231.602802	-231.450930	-231.445302	-234.543078	-234.402360	-234.396016
*Reactant (1,3-hexadiene with Ci symmetry)*	-231.692535	-231.539543	-231.532565	-234.611711	-234.469215	-234.461866

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	45.71	43.38	34.08	33.19	33.5 ± 0.5
ΔE (Boat)	55.61	54.76	41.95	41.78	44.7 ± 2.0

Nf710 (talk) 12:42, 4 November 2015 (UTC)IRC done well and tables presented very nicely, re optimization of the your TS done correctly however you havent compared the geometries or imaginary frequencies. very nice comparison with experiment. In general a well rounded report but some lacking knowledge in the theory of the optimisations work particulary with the second derivatives and what it represents.

Appendix, Log Files

Anti

Gauche

Anti with Ci symmetry

Anti with Ci symmetry at B3LYP/6-31G* optimisation

Anti with Ci symmetry at B3LYP 631-G* optimisation and frequency analysis

Chair TS using TS(Berny)

Chair TS using freezing coordinate

boat TS using QST2 1st attempt

boat TS using QST2 2nd attempt

IRC with 50 steps run on chair TS

Diels-Alder Cycloaddition

There are two Diels-Alder reaction being studied in this experiment: reaction between cis-butadiene and ethene and reaction between cyclohexa-1,3-diene and maleic anhydride. Similar to the cope rearrangement, reaction occurs in a concerted fashion via a cyclic transition state.

Diels-Alder reaction between cis-butadiene and ethene

Figure 6: Mechanism of Diels-Alder between cisbutadiene and ethene

Molecule of cis-butadiene and ethene were drawn and optimised to minimum separately using semi-empirical/AM1 theory level. Their optimised structures were put together resembling envelope-like transition structure, with maximum π-orbital overlapping between cis-butadiene and ethene. Freezing reaction coordinate was chosen to optimise transition state at semi-empirical AM1 theory level. The result of this calculation is re-optimised to TS(Berny) at B3LYP/6-31G* theory level. Transition structure is found since only one imaginary vibrational frequency is located, indicating it is at its saddle point.

Optimised cis-butadiene at semi-empirical/AM1 theory level has energy of 0.04879719 Hartrees and symmetry of C2v. Its HOMO is anti-symmetric about C2-C3 plane whereas its LUMO is symmetric about the plane.


Labelled cis-butadiene and ethene in Diels-Alder reaction	HOMO of cis-butadiene, anti-symmetric	LUMO of cis-butadiene, symmetric

Optimised transition structure at B3LYP/6-31G*

Energy at semi-empirical/AM1

Energy at B3LYP/6-31G*

Negative vibrational frequency at semi-empirical/AM1 /cm^-1

Negative vibrational frequency at B3LYP/6-31G* /cm^-1

HOMO/symmetry with respect to C2-C3 plane

LUMO/symmetry with respect to C2-C3 plane

0.11165482 Hartrees

-234.54388562 Hartrees

-955.87

-526.79

anti-symmetric

symmetric

IRC was being carried out on both optimised transition state using semi-empirical/AM1 and B3LYP/6-31G* respectively. In both cases, the graph of gradient along IRC starts and returns to zero, indicating transition state has been successfully characterised and reacted to form product. However, only forward direction was ran. IRC should have been run in both directions to check if transition structure could lead to both reactant and product at minimum of potential energy surface. If transition structure has been successfully characterised, IRC gradient graph would start at zero and return to zero as it approaches both ends of graph, simulating reaction pathway between transition state to reactant and product respectively.

Level of Theory	Number of Points Set	Graph of Gradient along IRC
AM1 semi empirical	100	Caption
B3LYP/6-31G*	150	Caption

IRC of transition state at B3LYP/6-31G* was firstly calculated using 100 steps. However, this did not lead to convergence of RMS gradient graph to zero. Therefore, more steps in reaction pathway are examined and graph approaches closer to zero as result - transition state has been found.

C-C distances in optimised transition state is measured and recorded.

Calculation theory method	C4-C5 distance Å	C1-C6 distance Å	C2-C1/C3-C4 distance Å	C2-C3 distance Å	C5-C6 distance Å
Semi-empirical/AM1	2.11906	2.11995	1.38192	1.39760	1.38284
B3LYP/6-31G*	2.27207	2.27210	1.38308	1.40720	1.38608

Literature C=C bond length, C-C bond length and C Van der Waals Radius are 1.334 Å, 1.544 Å and 1.700 Å respectively. In both calculation theory levels, distances between C4 and C5 as well as between C1 and C6 are longer than both C-C single and double bonds, but shorter than 2 x Van der Waals Radius of carbon. This indicates the partial formation of new C-C sigma bond between the terminal carbon atoms of the reactants. Other carbon bond lengths are longer than C=C bond but shorter than C-C bond, suggesting the molecule is at its transition state, where bond is forming and breaking at the same time. Therefore bond length information also confirms the structure optimised is the transition structure of Diels-Alder between cis-butadiene and ethene.


Vibration at -526.79cm^-1, bond formation is synchronous at transition state	Vibration at lowest positive frequency, 136.15^-1, bond formation is asynchronous as reaction proceeds

(The reaction will not proceed through the lowest positive frequency Tam10 (talk) 12:26, 27 October 2015 (UTC))

By examining and visualising the symmetry property of HOMO and LUMO of transition structure, it is possible to predict the MOs of reactants involved in the Diels-Alder cycloaddition. For Diels-Alder reaction to occur, LUMO of one reactant must react with HOMO of another reactant with the same symmetry. Reaction can only happen if there is significant overlap between the two MOs and this happens when the two MOs have the same symmetry. Therefore, the anti-symmetric HOMO of the transition state must have been formed from the anti-symmetric HOMO of cis butadiene and the antisymmetric LUMO of ethene while the symmetric LUMO of the transition state must have formed from the symmetric LUMO of cis-butadiene and symmetric HOMO of ethene.

(Images of the MOs of ethylene should be included Tam10 (talk) 12:26, 27 October 2015 (UTC))

Diels-Alder reaction between cyclohexa-1,3-diene and maleic anhydride

In this Diels-Alder reaction, the idea of regio-selectivity is being explored. Cyclohexa-1,3-diene and maleic anhydride can approach each other in two different orientations, leading to exo and endo products.

Molecules of cyclohexa-1,3-diene and maleic anhydride were built and optimised to minimum at semi-empirical/AM1 theory level. These optimised molecules were put together to form a guessed exo and endo transition state structure for Diels-Alder reaction between cyclohexa-1,3-diene and maleic anhydride. Method that involves freezing reaction coordinate was again carried out at semi-emperical/AM1 theory level. The resulting optimised transition state was re-optimised again using TS(Berny) method at B3LYP/6-31G* theory level. However, QST2 had to be used to model exo transition state due to its complex geometry. Freezing coordinate method failed to characterise the guessed exo transition structure since its guessed structure did not resemble its actual transition structure. Hence, reactants and product of this Diels-Alder cycloaddition were drawn and correctly labelled on Gaussview, where QST2 was used to locate transition state that exists somewhere between reactants and product.

C-C bond lengths are measured and recorded for both exo and endo transition state.

Endo transition state:

Method of calculation	C17-C1 distance/Å	C4-C16 distance/Å	C1-C6/C4-C5 distance/Å	C1-C2/C4-C3 distance Å	C2-C3 distance/Å	C17-C16 distance/Å	C17-C18/C15-C16 distance Å	C5-C15 distance/Å	C6-C18 distance/Å
semi-emperical/AM1	2.16233	2.16242	1.39304	1.49050	1.52293	1.40850	1.48924	2.89218	2.89218
B3LYP/6-31G*	2.26923	2.26925	1.39124	1.51490	1.55808	1.39388	1.47945	2.98898	2.98897

Exo transition state

Method of calculation	C3-C15 distance/Å	C6-C17 distance/Å	C1-C6/C2-C3 distance/Å	C5-C6/C3-C4 distance Å	C15-C17 distance/Å	C17-C16 distance/Å	C17-C18/C15-C16 distance Å	C20-C2 distance/Å	C1-C19 distance/Å
semi-emperical/AM1	2.17038	2.17027	1.48976	1.39440	1.41012	1.52202	1.48819	2.94494	2.94543

C-C bond lengths in both endo and exo transition state are being measured and recorded. As mentioned above, literature C=C bond length, C-C bond length and C Van der Waals Radius are 1.334 Å, 1.544 Å and 1.700 Å respectively. Some C-C bonds are longer than C=C double bond but shorter than C-C single bond, suggesting geometry is somewhere along the reaction pathway between reactants and product. At semi-emperical/AM1 theory level, the distance between the –(C=O)-O-(C=O)- fragment of maleic anhydride and the C atoms of the opposite -CH=CH- in endo transition state is found to be 2.89218 Å, which is shorter than the distance between the –(C=O)-O-(C=O)- fragment and –CH2-CH2- fragment in exo transition state which is 2.98897 Å. Both of these distances are shorter than 2 x Carbon Van der Waals forces, indicating there are some interactions between carbon atoms forcing carbon atoms to be closer together. The distance between carbon atoms where new sigma bond forms is 2.16233/2.16242 and 2.17038/2.17027 in endo and exo respectively. This is again shorter than 2 x Carbon Van der Waals Radius, indicating attractive interactions between carbon atoms. In this case, the distances in endo transition state are also shorter. The shorter the C-C distance, the greater the favourable interactions between Carbon atoms. Therefore, less strain is present in endo transition structure whereas exo transition structure experiences a greater amount of strain since the greater values of distances indicate C-C interaction is not as favourable as in endo form. Secondary orbital effect in endo structure can also be seen since it stabilises the endo structure, bringing carbon atoms closer together, leading to smaller C-C distances between –(C=O)-O-(C=O)- fragment and CH=CH fragment and shorter partially formed sigma C-C bond.

Molecules	HOMO	LUMO
Endo TS	HOMO of endo TS	LUMO of endo TS
Exo TS	HOMO of exo TS	LUMO of exo TS
Maleic anhydride	HOMO of maleic anhydride	LUMO of maleic anhydride
1,3-cyclohexadiene	HOMO of 1,3-cyclohexadiene	HOMO of 1,3-cyclohexadiene

These molecular orbitals are captured at semi-empirical/AM1 theory level. HOMO of maleic anhydride and LUMO of 1,3-cyclohexadiene is symmetric whereas LUMO of maleic anhydride and HOMO of 1,3-cyclohexadiene is anti-symmetric. However, HOMO and LUMO of both exo and endo transition state are anti-symmetric.

	HF/3-21G			B3LYP/6-31G(d)
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
1,3-Cyclohexadiene	0.02771129	0.152502	0.157726
Maleic acid	-0.12182418	-0.077322	-0.0721119
Endo TS	-0.05150480	0.133494	0.143684	-612.68339576	-612.502208	-612.491836
Exo TS	-0.05041976	0.134882	0.144883	-612.67933542	-612.498004	-612.487667

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Endo)	35.97	36.44
ΔE (Exo)	37.46	37.20

(There are no units in this table. In addition, you need to clarify whether you're talking about the activation energy or the reaction enthalpy Tam10 (talk) 12:26, 27 October 2015 (UTC))

This shows activation energy for the reaction via endo transition structure is lower, making endo product much more preferred than the exo product.

("Preferred" is a little too vague. It's best to distinguish between kinetics and thermodynamics Tam10 (talk) 12:26, 27 October 2015 (UTC))

IRC was carried out on both endo and exo to confirm the formation of transition state in the forward direction only. Both directions should have been run to confirm the reaction pathway from transition state to both reactant and product.

RMS gradient along IRC for endo TS, at semi-empirical/AM1 theory level with 100 steps. Gradient converges to zero, showing formation of transition state.

RMS gradient along IRC for endo TS, at DFT/B3LYP/6-31G* theory level with 100 steps. However, the graph is only approaching zero but not reaching it. IRC needs to be run with more steps in order to confirm transition state in this case. DFT/B3LYP/6-31G* is theory at a higher level and therefore it does caculation more accurately than semi-empirical/AM1 method. Hence, more IRC steps should be carried out to confirm the presence of its transition state.

RMS gradient along IRC for exo TS, at semi-empirical/AM1 theory level with 100 steps.

RMS gradient along IRC has approached zero for exo TS, at semi-empirical/AM1 theory level with 100 steps.

(There is no discussion about orbital overlap effects or sterics Tam10 (talk) 12:26, 27 October 2015 (UTC))

Appendix Log files

At semi-empirical/AM1:

TS in D-A between cis-butadiene and ethene at AM1

IRC with 100 steps on TS of cis-butadiene and ethene

At 6-31G*:

TS in D-A between cis-butadiene and ethene at 631G*

IRC with 200 steps on TS of cis-butadiene and ethene at 631G*

At semi-empiricial/AM1:

Endo TS in D-A between cyclohexadiene and maleic anhydride

Endo TS in D-A between cyclohexadiene and maleic anhydride IRC at 100 steps

Endo TS in D-A between cyclohexadiene and maleic anhydride

Endo TS in D-A between cyclohexadiene and maleic anhydride IRC at 100 steps

At 6-31G*:

Endo TS in D-A between cyclohexadiene and maleic anhydride

Endo TS in D-A between cyclohexadiene and maleic anhydride IRC

Reference

Conformational Study of 1,5-Hexadiene and 1,5-Diene-3,4-diols, Benjamin W. Gung, Zhaohai Zhu, Rebecca A. Fouch J. Am. Chem. Soc., 1995, 117 (6), pp 1783–1788 DOI: 10.1021/ja00111a016 Publication Date: February 1995

Organic Chemistry by Jonathan Clayden, Nick Greeves, Stuart Warren.

Pauling, L. (1931). THE NATURE OF THE CHEMICAL BOND. II. THE ONE-ELECTRON BOND AND THE THREE-ELECTRON BOND. J. Am. Chem. Soc., 53(9), pp.3225-3237. doi:http://pubs.acs.org/doi/abs/10.1021/ja01360a004

Density Functional Theory Isotope Effects and Activation Energies for the Cope and Claisen Rearrangements J. Am. Chem. Soc., 1994, 116 (22), pp 10336–10337, DOI: 10.1021/ja00101a078, Publication Date: November 1994