Rep:Mod:SergioGeorgini
Module 1
Samuel Murphy
Aims
Three primary methods were learnt and applied to evaluate the structural and spectroscopic properties of a number of molecules. Firstly, the basic techniques of molecular mechanics, using the Allinger MM2 molecular mechanics models implemented on ChemBio3D Ultra, were used to investigate the regioselectivity of the hydrogenation of cyclopentadiene dimer as well as atropisomerism of an intermediate in the synthesis of taxol. Secondly, semi-empirical molecular orbital modelling using MOPAC/PM6 was used to analyse the regioselective addition of dichlorocarbene and glycosidation in monosaccharide chemistry. Finally, a mini project was undertaken to differentiate between two different isomers of cubebol using DFT-based Molecular orbital methods combined with the methods previously learnt in the module.
Introduction/Background
With the development of more user friendly modelling software packages, synthetic chemists now have access to useful information and can obtain insights from computational calculations. The main uses of computational chemistry for synthetic chemists are that they are able to minimise and compare energies visually, predict spectra, calculate molecular orbitals and model transition states.[1]. These tools are important in time and cost saving as it removes the need for "trial and error" synthesis. If a transition state is modelled and shown to be too high in energy to experimentally proceed, the synthetic chemist can move instead of trying the reaction in the lab. The MM2 method is a non-quantum mechanical model known as the Molecular Mechanics approach (MM). The model assumes the energy of a molecular system comprises essentially five additive (non-interacting) terms which are: diatomic bond stretches, triatomic bond angle deformations, tetra-atomic bond angle torsions, non-bonded Van der Waals repulsions and electrostatic attractions of individual bond dipoles.[2] This method is useful to find the optimal geometry and corresponding optimised geometry of a molecule. It also gives useful information like dihedral angles and torsion and Van der Waals energies. However, its flaws are that it cannot cope with unusual bonding or interaction, cannot predict molecular orbitals and cannot model bond-breaking transition states
Semi-empirical Molecular Orbital Theory trumps the non-quantum mechanical MM2 method as it can cope with unusual bonding like conjugation as well as modelling molecular orbital surfaces. It can cope with the elctronic aspects of reactivity and take the influence of electrons in a molecule on bonding and derived spectroscopic properties.[3]
Modelling using Molecular Mechanics
The Hydrogenation of Cyclopentadiene Dimer
The endo-/exo- selectivity of cyclopentadiene dimerisation
Theoretically, cyclopentadiene could dimerise to form one of two diesteroisomers, either the exo- or the endo-dimer via a Diels-alder π4s + π2s cycloaddition (figure 1). However, experimentally, the dimerisation procedes with specific formation of the endo- dimer rather than the exo-.
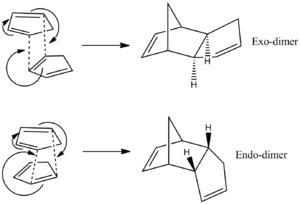
The product formed depends on the orientation of the dienophile to the diene as shown above but thermodynamics vs. kinetics needs to be considered. Under thermodynamic control, the most stable final product would be formed but if under kinetic control the product with the most stable transition state would be formed. Allinger MM2 force field was used to optimise the geometry of the two diasterosiomers isomers in order to determine the most thermodynamically product ie. the isomer with the lowest total energy (table 1).
| Component | Energy of Exo dimer/ (kcalmol-1) | Energy of Endo dimer/ (kcalmol-1) |
|---|---|---|
| Stretch | 1.2860 | 1.2511 |
| Bend | 20.5804 | 20.8464 |
| Stretch-Bend | -0.8384 | -0.8354 |
| Torsion | 7.6546 | 9.5110 |
| Non-1,4 Van der Waals | -1.4158 | -1.5433 |
| 1,4 Van der Waals | 4.2321 | 4.3200 |
| Dipole/Dipole | 0.3775 | 0.4476 |
| Total Energy | 31.8765 | 33.9975 |
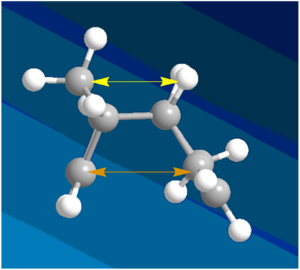
The results of the molecular modelling showed that the exo-dimer was the more thermodynamically stable as it had a lower total energy of 31.8765 Kcal/mol compared to the total energy of 33.9975 Kcal/mol for the endo-dimer. The primary reason for this energy difference is the lower torsion energy of the exo- (7.6546 Kcal/mol) compared to the endo- (9.5110 Kcal/mol) due to steric strain and hindrance. One source of strain, in the endo-isomer, is the repulsion between the bridge-head carbon and the two hydrogens pointing in the same direction as the bridge-head (figure 2 - yellow arrow. This strain is not present in the exo- form as those two hydrogens are pointing in the opposite direction away from the bridge-head. The second source of strain is the 1,4 steric strain shown as the orange arrow in figure 2. Again, this strain is not present in the exo-form as the 5 membered ring is pointing upwards and away, resulting in less steric strain.
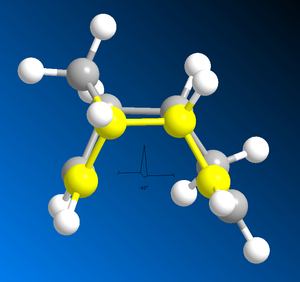 |
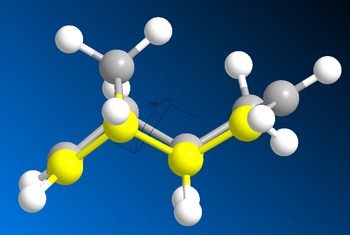 | |||
The exo-dimer displays a dihedral angle of 179o which is close to the ideal 180o anti-periplanar conformation with the lowest torsion energy. The endo-dimer dihedral measurement of 46o is in between a gauche and a total eclipsed conformation which are both high in energy than the anti-periplanar arrangement and so the endo-dimer has higher torsional energy.
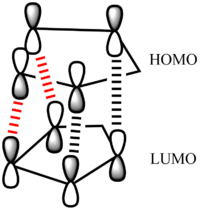
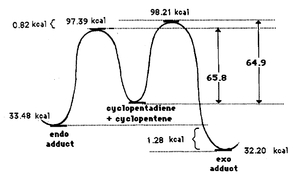
Therefore, the fact that endo-dimer is specifically produced experimentally indicates that the dimerisation is under kinetic control. If it were under thermodynamic control the exo-dimer would be formed as it is the more stable of the two isomers. Proceding via a pericyclic reaction, this stereospecific preference for the endo- isomer is due to the electronic properties of the molecules which can be understood in terms of frontier molecular orbitals. Primary orbital overlap need to be considered between the HOMO of the diene and the LUMO of the dienophile as shown in figure 3 for the endo- isomer (black lines). However this overlap is similar in the exo-product so there must be another overlap which favours the endo- dimer. This extra overlap is the secondary orbital overlap (SOO) which is the positive overlap of frontier molecular orbitals of the nonactive frame (figure 3 - red lines). This SOO is only present in the endo- tansition state and not in the exo- and so the energy is lowered thereby favouring the endo- isomer productowever, this cannot be modelled using a molecular mechanics. The energies of both transition states have been measured in literature and it has been shown that the endo- transition state is ~1 Kcal/mol lower than the exo- transition state. This is illustrated in the graph in figure 4[4].
Hydrogenation of the endo- isomeric cyclopentadiene dimer
Dihydro derivatives
Hydrogenation of the endo dimer initially gives one of the dihydro derivatives (3 or 4) depending on which carbon carbon double bond is hydrogenated (figure 5). This is due to regioselectivity unlike the stereoselective dimerisation.
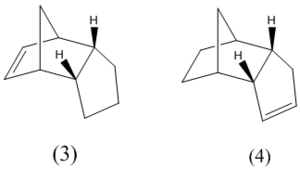
The geometries of these two derivatives were again optimised using Allinger MM2 force field and displayed in table 2 below along with several other interactions
| Component | Energy of Dihydro derivative 3/ (kcalmol-1) | Energy of Dihydro derivative 4/ (mol-1) |
|---|---|---|
| Stretch | 1.2771 | 1.0966 |
| Bend | 19.8664 | 14.5232 |
| Stretch-Bend | -0.8346 | -0.5493 |
| Torsion | 10.8068 | 12.4978 |
| Non-1,4 Van der Waals | -1.2257 | -1.0692 |
| 1,4 Van der Waals | 5.6330 | 4.5124 |
| Dipole/Dipole | 0.1621 | 0.1406 |
| Total Energy | 35.6850 | 31.1520 |
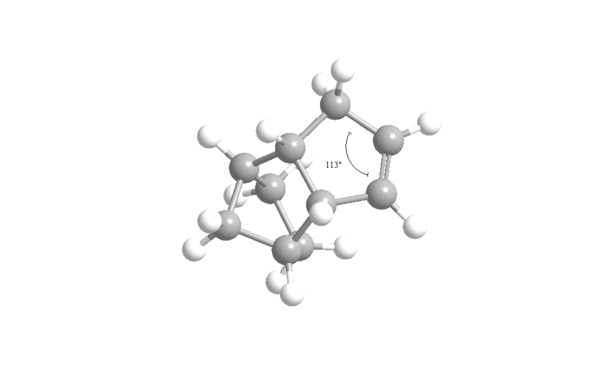
The results show that dihydro derivative 4 has a lower energy (31.1520 Kcal/mol) than dihydro derivative 3 (35.6850 Kcal/mol) so is therefore more thermodynamically stable. The main difference in energies is due to the difference in bend energy dependent on angular strain. The ideal bond angle for an sp2 hybridised carbon, like in the carbon-carbon double bond, free of strain is 120o. The ring strain in derivatives 3 and 4 compresses this angle raising the energy in the process. Using ChemBio3D, this angle was measured for the two derivatives shown in figures 6 and 7. The 108o of derivative 3 is further from the ideal 120o than the 113o of derivative 4 causing it to have more angular strain and hence have a higher energy. Furthermore, the 1,4 Van der Waals energy is higher for dihydro derivative 3 than derivative 4. Derivative 4 is thermodynamically the most stable product but that does not necessarily mean the dihydrogenation proceeds thermodynamically. Derivative 3 could well have a lower energy transition state and be the most kinetically stable product but transition state energies are unknown so this can only be speculated.
 |
 | |||
Tetrahydro derivative
The dimer eventually becomes fully saturated after prolonged hydrogenation to form the tetrahydro derivative shown below (figure 8). The hydrogenation equation from the dihydro- to the tetrahydro derivatives needs to be balanced by addition of H2 to the dihydro side but this makes no difference as the energy of dihydrogen is zero.
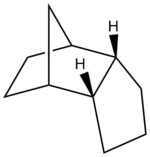
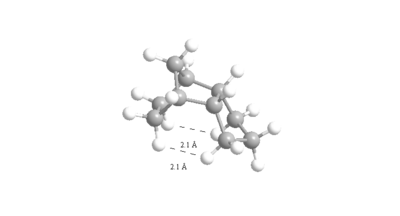
The optimised geometry was found (using MM2) to have a total energy of 36.0902 Kcal/mol. The sp2 hybridized carbons have been hydrogenated to sp3 carbons and so the ideal bond angle is now 109.5o. This causes torsional strain which raises the energy of the derivative compared to the unsaturated derivatives. There is also more repulsive Van der Waals interactions as there are more hydrogens due to the hydrogenation. This loss of planarity of the hydrogens (going from sp2 to sp3) means their interaction with the other atoms increases which raises the total energy of the derivative. These van der waals interactions both of 2.090 Å are ≤2.1Å (figure 9) and so are in the repulsive region.[5]
Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol
Atropisomerism of a key intermediate
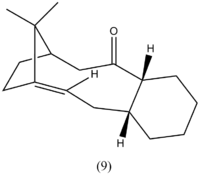
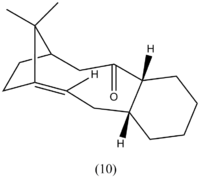
The anti-cancer drug Taxol is synthesised via a key intermediate whereby the carbonyl group either points up (9) or points down (10). On standing, intermediate 9 isomerises to 10 suggesting that 9 is the kinetic product with the most stable transition state and 10 is the most thermodynamically stable product with the lowest total energy. However, molecular mechanics was needed to confirm this predicition with the results shown below. These isomers are an example of atropisomerism as there is restricted rotation of the substituted aromatic rings within the macrocyclic taxol structure.[6] Further steps in the synthesis involve addition to the carbonyl so it is important to determine which form of the isomer is most stable. It was found that the cyclohexyl ring can either be in the energetically expensive twist-boat formation on in the more stable chair confomation. These two possible geometries (for both 9 and 10) were optimized using Allinger MM2 force-field. These structual images are shown below in table 3.
The different energy components and total energies were calculated with MM2 (table 4). MMFF94 was also used to calculate the total energy. MM2 and MMFF94 use different force-fields to calculate the optimum energy so they cannot be directly compared. However the relative energies between 9 and 10 can be compared with MM2 and MMFF94.
| Component | Energy of Intermediate 9 - twist boat/ (kcalmol-1) | Energy of Intermediate 9 - chair/ (kcalmol-1) | Energy of Intermediate 10 - twist boat/ (kcalmol-1) | Energy of Intermediate 10 - chair/ (kcalmol-1) |
|---|---|---|---|---|
| Stretch | 2.8775 | 2.7006 | 2.7103 | 2.6044 |
| Bend | 17.2803 | 15.8868 | 11.7407 | 10.4198 |
| Stretch-Bend | 0.4731 | 0.4176 | 0.3236 | 0.2908 |
| Torsion | 20.6082 | 20.3008 | 21.8690 | 19.3717 |
| Non-1,4 Van der Waals | -0.8920 | -1.3913 | -2.0978 | -2.2173 |
| 1,4 Van der Waals | 14.3717 | 13.2867 | 13.9193 | 12.9205 |
| Dipole/Dipole | -1.7088 | -1.6723 | -2.0316 | -2.0092 |
| Total Energy using MM2 | 53.0100 | 49.5289 | 46.4336 | 41.3808 |
| Total Energy using MMFF94 | 78.0026 | 73.8573 | 66.335 | 61.2032 |
The absolute difference in energy between 9 and 10 is an observable quantity directly related to the equilibrium constant between the two intermediates. The MM2 and MMFF94 methods agree with each other as for both methods, intermediate 9-twist boat(MM2 - 53.0100 kcalmol-1 and MMF94 78.0026 kcalmol-1) and intermediate 9- chair (MM2 - 49.5289 kcalmol-1 and MMF94 73.8573 kcalmol-1) are higher in total energy than intermediate 10-twist boat(MM2 - 46.4336 kcalmol-1 and MMF94 66.335 kcalmol-1) and intermediate 10- chair (MM2 - 41.3808 kcalmol-1 and MMF94 61.2032 kcalmol-1) respectively. Furthermore, the results show that for both intermediate 9 and 10, the isomer with the cyclohexyl chair is lower in energy as expected than the isomer with the the energetically expensive cyclohexyl twist-boat. This difference in energy is primarily due to bend energy as there is more angular strain in the twist-boat form. The cyclohexyl chair conformation is free of angular strain as all of the bond angles are the ideal 109.5o needed for an sp3 hybridised carbon. The 1,4 Van der Waals energies are also higher in the twist boat conformers relative to the corresponding chair conformers. Therefore, only isomers containing the chair conformation will be analysed. According to MM2, intermediate 9 (chair) has a higher total energy of 49.5289 kcalmol-1 than the 41.3808 kcalmol-1 of intermediate 10 (chair) (also confirmed with MMFF94). This confirms that intermediate 10 (chair) is the thermodynamic product as it more stable energy wise. Intermediate 9 (chair) initially forms as it is the kinetic product so must have a lower energy transition state but this cannot be modelled using MM2 as frontier molecular orbitals need to be calculated and are behind the limtits of MM". The MMFF94 results, compared relatively, show good agreement with MM2. The total energy of intermediate 10 (chair) is 82.9 % that of intermediate 9 (chair) according to MMFF94 which is similar to the 83.5 % using MM2. The main reason for this total energy difference is the bend energy which differs by 5.467 kcalmol-1. This shows that there is more ring strain in the in the intermediate when the carbonyl is pointing up compared to when it is pointing down.
Hyperstable olefins
In 1924, Bredt noted that double bonds tended to avoid bridge heads in macrocylic molecules (ring junctions) due to steric ring strain.[7] Despite this, several of these compounds were prepared but the carbon-carbon double bond was found to be highly reactive.[8] These molecules had a positive "olefin strain" (OS) energy which is defined as the strain energy of the most stable parent hydrocarbon subtracted from the strain energy of the olefin.[7] However, O.S Maier et al. discovered a new class of bridge-head compounds with a negative OS energy.[9]These compounds were named hyperstable olefins whereby the olefin is more stable than the parent hydrocarbon. Intermediates 9 and 10 are examples of these hyperstable olefins with high heats of hydrogenation favouring the olefin over the parent hydrocarbon. The geometry of the most stable isomer (intermediate 10 - chair) was again optimised using MM2 along with the resulting parent hydrocarbon. As intermediate 10 - chair and its parent hydrocarbon are not isomeric the hydrogenation equation needs to be balanced by adding a dihydrogen to the unsaturated side. However, when the geometry of H2 was optimised using MM2 it was found to have zero total energy. So in this case, balancing the equation has no effect on the comparison of energies but in other cases of more complex molecules it is important to include all energies. The results are shown below in table 5:
| Component | Energy of Intermediate 10 - chair/ (kcalmol-1) | Energy of Parent hydrocarbon of intermediate 10 -chair/ (kcalmol-1) |
|---|---|---|
| Stretch | 2.6044 | 2.8190 |
| Bend | 10.4198 | 13.6598 |
| Stretch-Bend | 0.2908 | 0.6432 |
| Torsion | 19.3717 | 21.7524 |
| Non-1,4 Van der Waals | -2.2173 | -2.6034 |
| 1,4 Van der Waals | 12.9205 | 15.7104 |
| Dipole/Dipole | -2.0092 | -1.7262 |
| Total Energy using MM2 | 41.3808 | 50.2552 |
| Total Energy using MMFF94 | 61.2032 | 72.7665 |
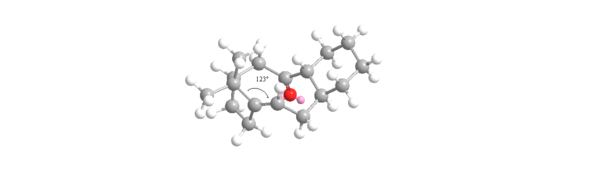
This gives a negative OS energy of -8.8744 kcalmol-1 (41.3808 - 50.2552) meaning the hyperstable bridge-head olefin is lower in energy and more stable than the parent hydrocarbon. The MMFF94 energy for the olefin is 84.1 % that of the parent hydrocarbon. This compares well relatively to the MM2 value of 82.3%. The hyperstable bridge-head olefin is more stable mainly due to having lower bending, torsion and 1,4 Van der Waals energies. In the unsaturated intermediate 10 -chair isomer, the carbons either side of the carbon-carbon double bond are sp2 hybridized so would ideally prefer a bond angle of 120o to the adjacent sp3 hybridized carbon. Conversely, in the saturated parent hydrocarbon isomer, the ideal bond angle is now 109.5o as the hybridization of that same carbon is now sp2. These two bond angles were calculated with the results shown below in figures 10 and 11:
 |
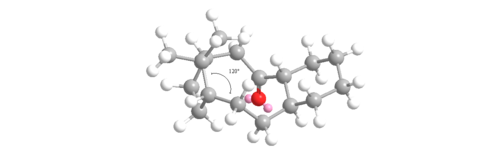 | |||
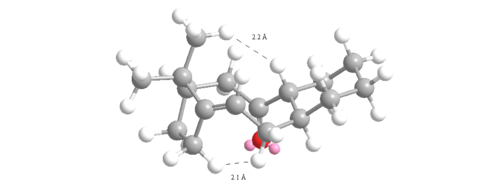
The angle measured for the unsaturated intermediate 10- chair is 123o which is only 3o away from the ideal 120o. However, the angle measured for the saturated intermediate 10-chair is 120o which is 10.5 o larger than the ideal 109.5o. Therefore, there is less angular ring strain and torsion in the unsaturated compared to the saturated intermediate leading to its hyperstability. The other reason for the hyperstability is the Van der Waals energies which are higher in the saturated than the unsaturated intermediate (15.7104 to 12.9205 kcalmol-1). If hydrogen atoms interact at distances ≤2.1Å then they are repulsive but if >2.1Å then they are attractive. Two of the interactions were measured for each intermediate and shown in figures 12 and 13:
 |
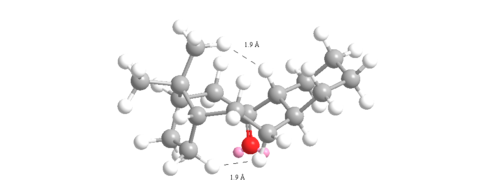 | |||
The intramolecular bond distances measured in the unsaturated intermediate are 2.087Å and 2.213Å so one is repulsing and one attracting. However, the same Van der Waals intermolecular bond distance measured for the saturated intermediate are both ≤2.1Å (1.948Å and 1.938Å) and so are both repulsive raising the energy of the intermediate. These reasons are why the hyperstable olefin reacts so slowly.
Modelling Using Semi-empirical Molecular Orbital Theory
Regioselective Addition of Dichlorocarbene
Upon addition of dichlorocarbene to 9-chloromethanonaphthalene (compound 12), π-selectivity dominates as the syn trichloride product (below in figure 14) is the only monoadduct isolated (72 % yield). The pentachloride diadduct is the other product isolated with a lower yield of 23 %.[10]
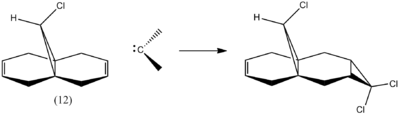
To understand and rationalise this π-selectivity, in terms of orbital control of reactivity, an approximate representation of the valence-electron molecular wavefunctions needed to be determined. This wave-description of the electrons marks the transition away from purely the classical mechanical treatment of molecules to the quantum mechanical treatment.
Part 1: Orbital control of reactivity
The geometry of the structure was first optimised using MM2 before applying an electronic method. The structure was then run on the MOPAC interface (on ChemBio3D) with method = PM6. The molecular surfaces property was chosen and the HOMO, presumed to be the most reactive towards electrophilic attack, as well as several other valence-electron molecular wavefunction were initially approximated. However, the first molecular wavefunction modelled (MOPAC/PM6 HOMO) did not reflect the molecular symmetry. This HOMO wavefunction shown below in figure 15 is clearly assymetric lacking the plane of symmetry cutting through the chlorine atom and both carbon-carbon double bonds of the molecule.

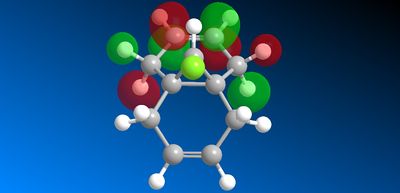
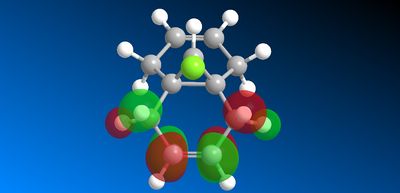
This asymmetry shows that there is a flaw in the MOPAC/PM6 method so another MOPAC interface method was therefore used instead to obtain symmetry reflecting that of the molecule. B. Halton et al [11] used the MOPAC/PM3 method successfully to also model compound 12 so this method was used to model the HOMO -1, HOMO, LUMO, LUMO +1 and LUMO + 2 valence electron molecular wavefunctions with 0.015 isocontour, shown below (figure 16).
| HOMO -1 | HOMO | LUMO | LUMO + 1 | LUMO + 2 |
|---|---|---|---|---|
 |
 |
 |
 |
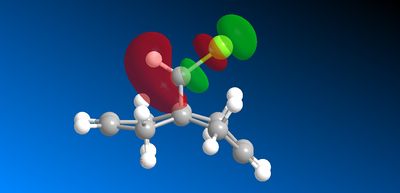 |
Figure 16: Valance electron molecular wavefunctions of compound 12
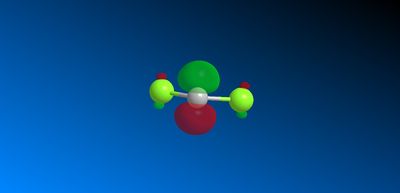
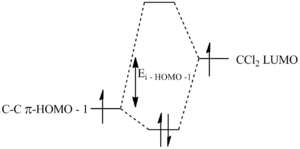
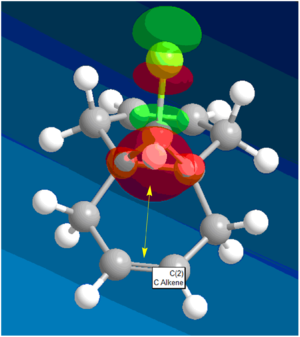
The question of regioselectivity about which pi face the dichlorocarbene will add to can be solved by looking at the HOMO molecular orbital. There is a large build up of electron density on the π-face syn to the chlorine which means this is the most nucleophilic alkene. This is important in discriminating between the two alkene bonds as the reaction with dichlorocarbene is similar to electrophilic addition. Therefore, this nucleophilic alkene will donate electron density to the LUMO of the electrophilic dichlorocarbene (figure 17) in an electrophilic attack. The π-face anti to the chlorine has no electron density (in the HOMO) according to the modelling so would not donate any electron density. However, The LUMO does show that the orbitals are located around the π-face anti to the chlorine. This suggests that this alkene would be susceptible to nucleophilic attack from an electron donating nucleophile. Therefore, according to this MOPAC/PM3 modelling, the dichlorocarbene would add to the alkene syn to the chlorine as is seen experimentally.
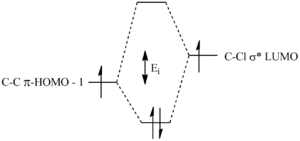
It can be seen that the HOMO -1 orbital has a large build up of electron density on the π-face syn to the chlorine so this face could act as a nucleophile and attack the dichlorocarbene. However, according to the Klopman Salem equation [12], stabilisation energy (Estab is directly proportional to the square of the overlap integral divided by the interaction energy (Ei). This interaction energy is is the difference in energy between overlapping orbitals and the smaller the value, the larger the stabilisation energy.
It can be seen that the interaction energy is smaller for the HOMO overlap than for the HOMO -1 overlap and so Estab is larger for the former.
Another reason for the regioselective preference of the syn π face is that there is a stabilising interaction between the anti π-face and the C-Cl σ* orbital (LUMO + 2). This results in the anti π orbital (HOMO -1) to be more stabilised relative to the syn π-orbital (HOMO) (figure 18). This overlap is not present for syn π-orbital rendering it more susceptible to electrophilic attack of the dichlorocarbene.
Part 2: The influence of the Cl-C bond on the vibrational frequencies
The influence of the C-Cl bond vibrational frquencies of the molecule were calculated by comparing compound 12 and its monohydrogenated derivative (with the syn C=C bond intact). After optimising the geometry with MOPAC/PM6, an input file was saved to run B3LYP/6-31G(d,p) on the Gaussian interface. This was done for both molecules before saving as gjf. files and editing on wordpad so that the top line read # b3lyp/6-31G(d,p) opt freq. The two input files were submitted to scan and the resulting formatted check point files opened on GaussView 5.0.9 and analysed.
The two calculated IR vibrational spectra are shown below in figure 19:
| Compound 12 D space | Compound 12's monohydrogenated derivative D space |
|---|---|
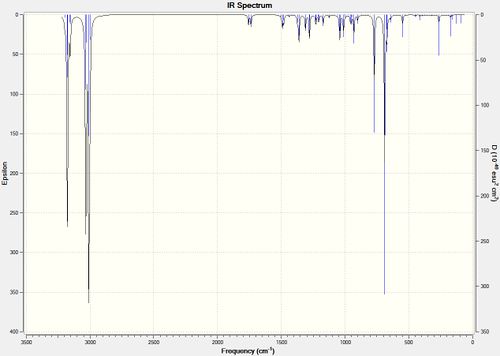 |
 |
Figure 19 : The calculated IR spectra of Compound 12 dihydro derivative
The C-Cl stretches were inspected and the two C=C stretches for the diene (compound 12) and the single stretch for the monohydrogenated derivative identified (monoene). Their frequencies are shown below in table 6
| Compound (symmetry) | C=C stretch - syn (cm-1) | C=C stretch - anti(cm-1) | C-Cl stretch (cm-1) | |
|---|---|---|---|---|
| Compound 12 (Cs) | 1757.37 | 1737.11 | 770.91 | |
| Compound 12' monohydrogenated derivative (C1) | 1753.76 | x | 779.93 |
The frequency of the C-Cl stretch in the monohydrogenated derivative (779.93 cm-1) is higher than the C-Cl stretch in compound 12 (770.91 cm-1) showing it has increased in strength. This agrees with the analysis in part 1 regarding the donation of electron density from the anti-π face (HOMO - 1) into the C-Cl σ* orbital (LUMO + 2). Filling of this anti-bonding obital weakens the C-Cl bond in compound 12. However, the anti-π face is not present in the monohydrogenated product meaning there is no donation to the orbital so the C-Cl bond is therefore stronger than in the diene.
Monosaccharide chemistry: glycosidation
The neighbouring group effect can force almost complete diastereospecifity either the alpha or beta anomer in glycosidation. To form the beta anomer the adjacent OAc group has to attack from the bottom of the ring to form the oxonium cation which allows nucelophilic attack above the ring. Conversely. the alpha anomer is formed by the oxonium cation intermediate forming on the top face of the ring allowing the nucleophile to add anomerically on the bottom face. This is shown below in figure 19 [13].
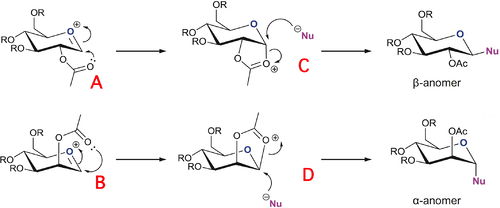
Before the structures were sketched it was decided that an appropriate R group to represent the chemistry while keeping the computational demand minimal would be R=Me. If R=Ac was used, as is usually used in protecting group chemistry, the computational demand would be too high for the methods used due its size and increased hydrogen bonding. However, if R=H was used, it would not be a true representation of the sterics in the ring. It was decided that the MOPAC/PM6 method was better suited for the task than the MM2 method as the latter only works well for simple hydrocarbons with just a few substituents and cannot cope with unusual bonding or interactions like carbocations and conjugation. Also, the semi-empirical MOPAC/PM6 is better suited to modelling the neighbouring group effect as is required as it can model conjugation in molecules.. A and B are when the acetyl group is pointing below the plane of the oxonium cation whereas A' and B' are when they point above. Likewise C and D are when the oxonium ring points below the plane of the molecule whereas C' and D' are when it points above. Images of these jmols are shown below in figure 20:
| A | A' | B | B' | C | C' | D | D' |
|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
Figure 20: J Mol images of A, A', B, B', C, C', D and D'
The geometries of the structures shown above were optimised and energies minimised using Allinger MM2 force-field and MOPAC/PM6 with the results shown below in table 7. In each case, the MM2 geometry was used as the starting point for obtaining the PM6 geometry.
| Component | Energy of A MM2 and PM6/(kcalmol-1) | Energy of A' MM2)and PM6(kcalmol-1) | Energy of B MM2 and PM6 /(kcalmol-1) | Energy of B' MM2 and PM6/(kcalmol-1) | Energy of C MM2 and PM6/(kcalmol-1) | Energy of C' MM2 and PM6/(kcalmol-1) | Energy of D MM2 and PM6/(kcalmol-1) | Energy of D' MM2 and PM6/(kcalmol-1) | |
|---|---|---|---|---|---|---|---|---|---|
| Stretch | 2.6707 | 2.5528 | 2.468 | 2.6004 | 1.7911 | 2.7921 | 2.7077 | 1.9074 | |
| Bend | 11.7215 | 8.6069 | 9.4604 | 12.1232 | 16.7074 | 18.5139 | 20.6730 | 21.2521 | |
| Stretch-Bend | 0.9734 | 0.9221 | 0.9064 | 0.8869 | 0.7530 | 0.8843 | 0.8669 | 0.8154 | |
| Torsion | 1.8441 | 3.5586 | 3.1489 | 2.6201 | 7.6987 | 9.0568 | 7.8668 | 7.4818 | |
| Non-1,4 Van der Waals | 1.6890 | -2.5681 | -2.6296 | 1.4638 | -4.0374 | -2.0970 | -2.6482 | -2.8266 | |
| 1,4 Van der Waals | 19.1122 | 19.5047 | 19.1629 | 19.8778 | 17.4106 | 19.0514 | 18.3036 | 16.6698 | |
| Charge/Dipole | -32.9145 | -1.4833 | -1.0194 | -37.9911 | -5.0966 | -0.3640 | -1.1547 | -7.7978 | |
| Dipole/Dipole | 8.0355 | 3.1907 | 3.9632 | 6.3753 | -1.0251 | -1.4280 | -1.1256 | -1.8637 | |
| Total Energy using MM2 | 13.1219 | 34.2844 | 35.4796 | 7.9564 | 34.2016 | 46.4093 | 45.4894 | 35.6384 | |
| ΔH energy of formation using MOPAC/PM6 | -91.65906 | -77.39802 | -77.51015 | -88.53139 | -91.65466 | -66.84000 | -67.00276 | -88.72917
|
For the A/A' pair the lowest energy for both the MM2 and MOPAC/PM6 methods are when the acetyl group is pointing below the oxonium cation so A'. The main cause for this energy difference is evidently from the difference in charge-dipole energy. For the B/B' pair, the lowest energy for both the MM2 and MOPAC/PM6 methods are when the acetyl group is pointing above the oxonium cation so B' again owing to difference in charge-dipole energy. Similar to the A/A' pair, the C form of the C/C' pair is lower in energy as the oxonium ring is pointing below the plane of the molecule. Much like the B/B' pair the D' form in the D/D' pair is lower in energy as the oxonium ring is pointing above the plane of the molecule.
It can also be seen that the ΔH of formation for A and C is the same to 3sf (-91.7 kcalmol-1) as well as that for B' and D' (-89 kcalmol-1 3sf) However, the energies modelled using MM2 are different which suggests a flaw in one of the methods. The 3 bond lengths for the MOPAC/PM6 structures measured below in figures 20a and 20b show are the same for both A and C (same results for B' and D' but not shown). The corresponding compounds have the same structure and geometry but different bonding which suggests that the MOPAC/PM6 method can handle changes in the bond but the classical molecular mechanical MM2 method cannot. MOPAC/PM6 treats the two isoenergetic compounds as non-classical carbocations which incorporates the neighbouring group effect of the acetyl group. The MOPAC/PM6 method forms the most stable intermediate if the orientation of the acetyl group is right (ie below the plane for A/C and above the plane for B/D. The MM2 method is flawed as it treats the system as a classical carbocation lacking in conjugation so does not incorporate the neighbouring group effect.
 |
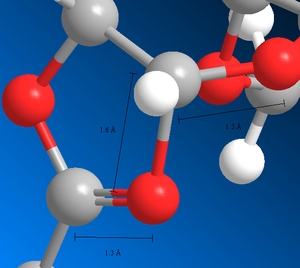 | |||
The diastereospecificity of the glycosidation can be rationalised looking at the energies of intermediates C/C' and D/D'. C is lower in energy than C' and also has better orientation for nucelophilic attack on the oxonium carbocation. Therefore, intermediate C forms the beta anomer. Similarly, D' is lower in energy than D and has better orientation and so the alpha anomer is formed. boltzmann ratios and predict/rationalise the diastereoselectivity of the reactions? The relative abundances of C/C' and D/D' were calculated using Boltzmann distribution to find the ratios of C:C' and D:D'. The lowest energies from the two pairs (lowest state i=0) were made zero energy. So for C/C* the energy of C (i=0) (-91.65466 kcalmol-1) was made zero and the energy of C' (i=1) was made 28.81466 kcalmol-1 as it is this much high than C energy. The Boltzmann distribution was then calculated for each energy and abundancies compared (table 7a).
| Boltzmann distribution for C (i=0) and C' (i=1) | Boltzmann distribution for D' (i=0) and D (i=1) |
|---|---|
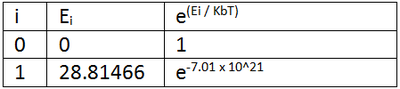 |
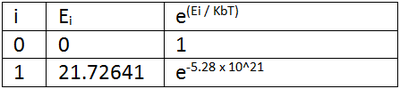 |
Table 7a : The Boltzmann distribution for C/C' and D/D'
The ratio of C:C' is effectively 1:0 as the value for C' is so small. This means that the intermediate C is effectively 100% abundant which supports the stereoselectivity already mentioned. Similarly, the ratio of D:D' is effectively 0:1 as the D value is so small. So intermediate D' is effectively 100 % abundant again supporting the stereoselectivity mentioned above.
Structure based Mini project using DFT-based Molecular orbital methods
The total synthesis of (-)Cubebol
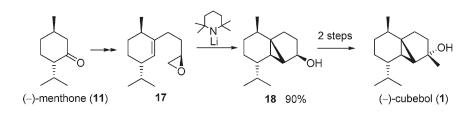
The total synthesis of the cooling agent cubebol, a natural sesquiterpene alcohol with a cooling and refreshing taste has recently been reported[14]. The last few steps of this total synthesis are shown in figure 20. DFT-based molecular orbital methods was used to calculate the spectroscopic information about two isomers of cubebol (one being (-)-cubebol) shown below in figure 21.The data gathered will be compared and contrasted with that in the literature. There are several stereocentres but only that affected by the final synthesis step was considered (figure 21). Therefore, the stereochemistry of the -OH and methyl group has been inverted from (-)-cubebol to form isomer 2 but all other stereocentres kept the same. The absolute configuration noted in the literature will be modelled and tested along with isomer 2 to see if the assignment is correct or if another isomer is actually produced.The isomeric products will be differentiated spectroscopically using 13C NMR, vibrational frequencies (IR) and optical rotation analysis. The 13C NMR spectra could show different chemical shifts which will be compared with the literature. Furthermore, there should be a key difference in optical rotation with only one matching the literature. Likewise, the IR spectra might show peaks at slightly different frequencies.The mechanism will also be analysed and discussed and the molecular orbitals modelled (MOPAC/PM3) to see why the reaction shows selectivity for one particular isomer. The geometry of the two isomers will be minimised using MM2 and MOPAC/AM1 giving a break-down as before of the different minimised energy components.
| Component | Energy of (-)-cubebol (1)/ (kcalmol-1) | Energy of diastereoisomer (2)/ (kcalmol-1) |
|---|---|---|
| Stretch | 2.2431 | 2.1171 |
| Bend | 9.6588 | 9.2921 |
| Stretch-Bend | -0.5139 | -0.4382 |
| Torsion | 20.9652 | 19.6557 |
| Non-1,4 Van der Waals | -3.5055 | -3.9401 |
| 1,4 Van der Waals | 9.6755 | 9.4554 |
| Dipole/Dipole | 0.3501 | 0.2839 |
| Total Energy using MM2 | 38.8734 | 36.4259 |
| Total Energy using MOPAC/AM1 | -71.02497 | -71.03413 |
There is little difference between the total energies modelled using MM2 with the difference being down to increased torsional strain in isomer(1) raising its total energy. For the MOPAC/AM1 method the energies are even closer so more spectroscopic data needs to be calculated to distinguish the preferential diastereoisomer.
13C NMR spectral analysis
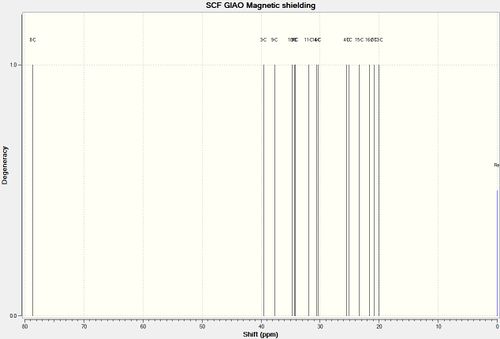
After geometry optimisation using MM2 and MOPAC/AM1 (on ChemBio3D) an input file was created on the gaussian interface with method DFT=mpw1pw91 and basis set 6-31G(d,p). The file was edited on wordpad so the top line read # mpw1pw91/6-31g (d,p) opt(maxcycle=25) and submitted to SCAN. The output file was then saved as a gjf file and edited in wordpad so the top line now read # mpw1pw91/6-31g (d,p) NMR scrf (cpcm, solvent=chloroform). This was submitted to SCAN and the NMR results from the formatted checkpoint file analysed.
| (-)-cubebol (1)D space | cubebol diastereoisomer (2)D space |
|---|---|
 |
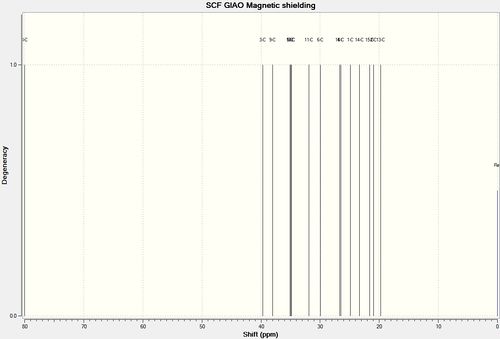 |
Figure 23 : The calculated 13C NMR dpectra of (-)-cubebol (1) and its diastereoisomer (2)
The carbons are assigned in figure below
| (-)-cubebol (1) | cubebol diastereoisomer (2) |
|---|---|
 |
 |
Figure 24 : The assignment of carbons in (-)-cubebol (1) and its diastereoisomer (2)
| Carbon | (-)-cubebol (1)δcalc (ppm) | cubebol diastereoisomer (2)δcalc (ppm) | (-)-cubebol (1)δlit[15] (ppm) | (-)-cubebol (1)(δcalc - δlit) (ppm) | cubebol diastereoisomer (2)(δcalc - δlit) (ppm) | |
|---|---|---|---|---|---|---|
| 8 | 78.6 | 80.0 | 80.3 | -1.7 | -0.3 | |
| 3 | 39.6 | 39.7 | 44.1 | -4.5 | -4.4 | |
| 9 | 37.7 | 38.0 | 39.0 | -1.3 | -1.0 | |
| 10 | 34.7 | 35.1 | 36.3 | -1.6 | -1.2 | |
| 5 | 34.3 | 35.0 | 33.6 | 0.7 | 1.4 | |
| 7 | 34.2 | 34.9 | 33.4 | 0.8 | 1.5 | |
| 11 | 32.0 | 31.9 | 31.7 | 0.3 | 0.2 | |
| 14 | 30.6 | 30.0 | 30.8 | -0.2 | -0.8 | |
| 6 | 30.3 | 26.7 | 29.5 | 0.8 | -2.8 | |
| 4 | 25.5 | 26.5 | 27.9 | -2.4 | -1.4 | |
| 1 | 25.1 | 24.9 | 26.5 | -1.4 | -1.6 | |
| 15 | 23.3 | 23.4 | 22.5 | 0.8 | 0.9 | |
| 16 | 21.6 | 21.6 | 20.1 | 1.5 | 1.5 | |
| 2 | 20.9 | 21.0 | 19.6 | 1.3 | 1.4 | |
| 13 | 20.1 | 19.8 | 18.7 | 1.4 | 1.1 |
There are no heavy atoms in the molecule like halogens so no spin orbit coupling error needed to be taken into account. The average deviation from the literature was calculated to be 1.38 and 1.43 ppm for (-)-cubebol (1) and its isomer (2) respectively. This shows accurate modelling as the deviation is small but does little to help distinguish between the two isomers prompting further spectroscopic analysis.
IR spectral analysis
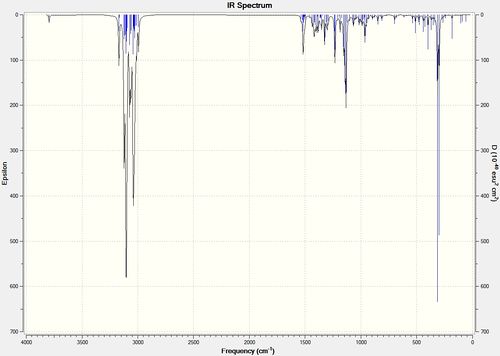
After geometry optimisation using MM2 (on ChemBio3D) an input file was created on the gaussian interface with method DFT=b3lyp and basis set 6-31G(d,p). The file was edited on wordpad so the top line read # b3lyp/6-31g (d,p) opt freq and submitted to SCAN. The vibrational spectra are shown below in figure 25:
| (-)-cubebol (1)D space | cubebol diastereoisomer (2)D space |
|---|---|
 |
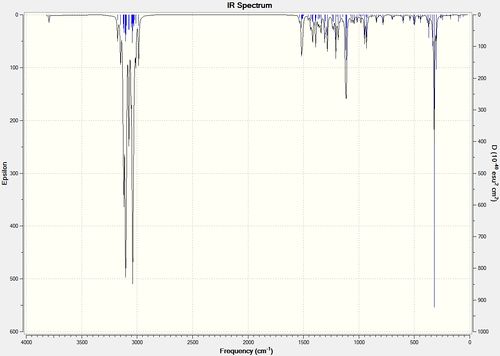 |
Figure 25 : The calculated IR spectra of (-)-cubebol (1) and its diastereoisomer (2)
The literature OH stretch is at 3380cm-1[14] which is lower than the modelled OH stretches of 3794.68 and 3794.04 cm-1 for isomers (1) and (2) respectively. There is little difference between the two calculated stretches and so the IR spectrum does not help in distinguishing between the two isomers. The optical rotation needs to be calculated to distinguish between the two diastereoisomers.
Optical rotation analysis
The optimised energy output file used for the NMR calculation was saved as a gjf file and edited on wordpad so the top line read # am-b3lyp/ 6-211G(d,p) polar(optrot) scrf(IEFPCM, solvent=chloroform) CPHF=RdFreq and the bottom line 589 nm. The file was then submitted to scan and the optical rotation found in the log output file. The results calculated are shown below in table 10:
| Compound | Optical rotation [α]25D | |
|---|---|---|
| (-)-cubebol (1) D space | 13.88 | |
| cubebol diastereoisomer (2) D space | -27.17 | |
| (-)-cubebol literature[14] | -27.9 |
The optical rotation has been the most useful tool in distinguishing between the isomers as they could clearly be distinguished from the results unlike the NMR and IR spectra. The results show that the optical rotation of -27.17o for diastereoisomer (2) is very close to the literature value of -27.9o. The value for (-)-cubebol (1) however is the wrong sign and far off at 13.88o. This suggests that diastereoisomer (2) is actually formed instead of (-)-cubebol (1)which is contrary to what the literature states.
Mechanistic analysis
The final synthesis step in the total synthesis of (-)-cubebol is the alkylation of norcubebanone carbonyl with the organolithium MeLi and CeCl3 (figure 26). The CeCl3 prevents the enolate ion from forming and makes sure the alkylation proceeds smoothly.
The proposed mechanism involves nucleophilic attack of the Me group to the electrophilic carbonyl carbon followed by acid hydrolysis to form the alcohol (figure 27).
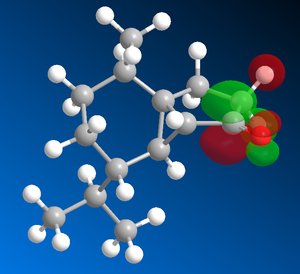
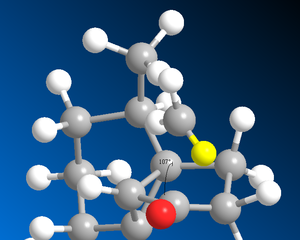
The sigma*C=O molecular orbital on the norcubebanone is filled with electron density from the Li-Me HOMO is a SN2 attack to form the cubebol (after hydrolysis)(figure 28). The two isomers can both be formed depending on which plane of the ring the Me- attacks from. If it attacks from above the plane, isomer (1) will be formed and if from below isomer (2) will be formed. Therefore, the Burgi-Dunitz (BD) trajectory of 107o has to be considered and steric hindrance looked at. It can be seen from figure 29 below that the attack from above and below the plane in terms of steric hindrance is similar. However, there appears to be more repulsive Van der Waals interactions (it seems more crowed when attacking from above as there are more hydrogens) when attacking above the plane which would favour the formation of isomer (2).
| LUMO of norcubebanone showing the sigma*C=O | HOMO of Li-Me |
|---|---|
 |
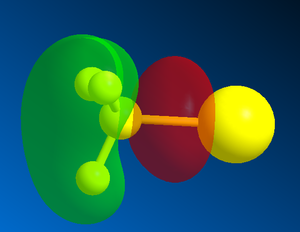 |
Figure 28 : Molecular orbitals: LUMO of norcubebanone and HOMO of Li-Me
| Attack from above the plane | Attack from below the plane |
|---|---|
 |
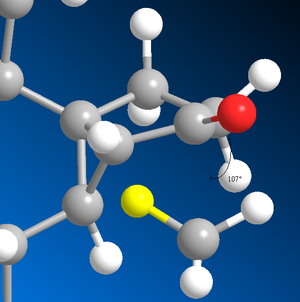 |
Figure 29 : Attack from above and below the plane along the Burgi-Dunitz trajectory of 107o
Further diastereoselectivity
Earlier on in the synthesis, there is another issue of diastereoselectivity (shown below in figure 29) when Lithium 2,2,6,6-tetramethylpiperidide (LTMP) induces an intramolecular cyclopropanation of epoxide (a) in t-BuOMe to give isomer (b) but isomer (c) could also be formed.
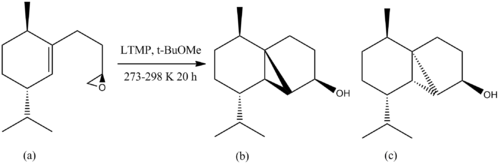
The geometries of the two isomers were firstly optimised using MM2 where it was calculated that isomer (b) had a higher energy than isomer (c) (37.2399 kcalmol-1 vs. 32.4653 kcalmol-1. Further modelling with MOPAC/PM6 showed that the energies of the optimised structures were the same to 2sf (-72 kcalmol-1). This suggests that there is litte difference in energy under thermodynamic conditions. The literature states that isomer (b) is preferentially formed in 90% yield[14] so it could be under kinetic control whereby the energy of the transition state for (b) is less than that of (c).
Conclusion
To conclude, the IR and NMR spectra calculated did little to help distinguish between the diastereoisomers. However, the optical rotation results showed a clear match with literature for isomer (2) suggesting that this is preferentially formed and not isomer (1) as the literature states. Furthermore, mechanistic analysis also showed that isomer (2) is the more likely product due to a less hindered Burgi-Dunitz trajectory path during the SN2 attack on the norcubebanone carbonyl to form (-)-cubole. Experimentally in the lab, the two isomers of cubebol could be distinguished by measuring the optical rotation with plane polarised light on an alpha D line.
References and citations
- ↑ https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:context
- ↑ https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:molecular_mechanics
- ↑ https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:organic#Modelling_Using_Semi-empirical_Molecular_Orbital_Theory.
- ↑ M. A. Fox et al, J. Org. chem.,1987, 52, 1471
- ↑ A. Bondi, J. Phys. Chem., 1964, 68 (3), 441
- ↑ P. Lloyd-Williams & E. Giralt., Chem. Soc. Rev., 2001, 30, 145
- ↑ 7.0 7.1 W. F. Maier, J. Am. Chem. Soc.,1981, 103, 1891
- ↑ G. A. Kraus et al., Chem. Rev., 1989, 1591
- ↑ Z. H. Li et al.,Tetrahedron Lett., ,1987, 28 (7), 753
- ↑ B. Halton et al., J. Org. Chem, 1991, 56, 5553
- ↑ B. Halton et al., J. Chem. Soc., Perkin Trans 2, 1992, 447
- ↑ A. J. StoneJ. Am. Chem. Soc., 1980, 102 (24), 7185
- ↑ https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:Anomer2.jpg
- ↑ 14.0 14.1 14.2 14.3 D. M. Hodgson, J. Org. Chem,2010 75 (7),2157
- ↑ B. Wu et al., Biosci. Biotechnol. Biochem.,2008, 72 (2), 611