Rep:Mod:Sc2108 Module 1

Introduction

In the last 25 years, computer modelling has had a significant impact on science and technology . especially chemistry where it is so much harder to illustrate atoms and bonds, never mind energy of reactions. Computational techniques were thus applied in this module in order to see how significant importance this has on chemistry in order to accurately model many aspects of structure and reactivity of the molecules. The main aims were to use molecular mechanics, semi-empirical molecular orbital theory and DFT method for calculations involving structure and spectroscopy. Firstly, molecular mechanics was used to predict the geometry and regioselectivity of the hydrogenation of cyclopentadiene dimer, stereochemistry of nucleophilic additions to a pyridinium ring and the conformation of a large ring ketone intermediate in Taxol formation. Semi-empirical methods were used to study the regioselectivity of the electrophilic carbenylation of a chloro-substituted bicyclic diene. Finally, DFT molecular orbital theory was used to inspect neighbouring group participation on the C-Cl and C=C stretching frequency of the previously investigated bicyclic diene. In the end, a mini project was conducted, investigating the two isomers from Diels Alder reaction and DFT molecular orbital theory was used to predict 13C NMR, IR and optical rotation.

Results and discussion

Isomerisation of cyclopentadiene

Cyclopentadiene dimerises into two possible isomers, endo and exo form. The endo dimer 2 is reported to be more favourable, although some of the exo dimer 1 is formed as well. An MM2 calculation was performed in ChemBio3D (12.0) in order to optimize geometries of the molecules and to obtain energies.

Figure 1: Optimised structures of Molecules 1 and 2

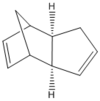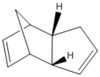Table 1: Relative Energies of Exo isomer 1 and Endo isomer 2

	Energies/ kcal mol-1
	Stretch	Bend	Stretch-Bend	Torsion	Van der Waals	Dipole-Dipole	Total
Exo isomer (1)	1.28	20.57	-0.83	7.67	4.24	0.38	31.88
Endo isomer (2)	1.25	20.86	-0.83	9.50	4.30	0.44	34.02

It can be seen from the table above, that the exo product is lower in energy than the endo form by 2.14 kcal/mol. This suggests that endo dimer is kinetically favourable and exo dimer is thermodynamically favourable product. It is reported that endo product is the major product , therefore this means kinetically favourable product is a major product and that this Diels Alder reaction is kinetically controlled. Hence, this also suggests that the reaction is not reversible, which is common for Diels Alder reactions. Thus, the dimerisation of cyclopentadiene is kinetically controlled, giving the endo dimer as a major product and exo dimer as a minor, thermodynamic product.

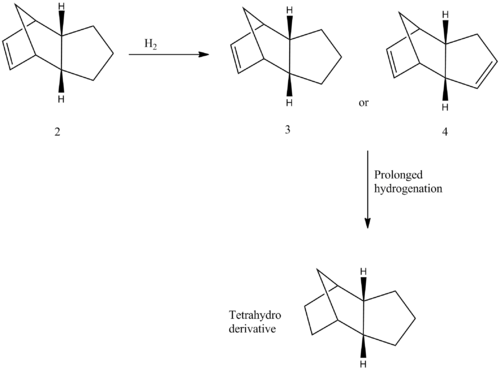
Hydrogenation of cyclopentadiene

Figure 2: Reaction mechanism of hydrogenation of endo dimer

Hydrogenation of the endo dimer is reported to give a dihydro derivative. Tetrahydro derivative, however, is formed only after a prolonged hydrogenation. There are two endo dimers, and in order to decide whether molecule 3 or 4 is formed, yet again, an MM2 calculation was carried out in order to optimize geometries and to obtain energies which are compared and summarised below.

Figure 3: Optimised structures of Molecules 3 and 4

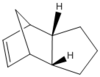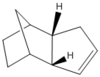Table 2: Relative Energies of Molecule 3 and Molecule 4

	Energies/ kcal mol-1
	Stretch	Bend	Stretch-Bend	Torsion	Van der Waals	Dipole-Dipole	Total
Molecule 3	1.27	19.94	-0.84	10.77	5.63	0.16	35.69
Molecule 4	1.13	13.08	-0.56	12.37	4.45	0.14	29.30

Dimer 4 is more stable than dimer 3 by 6.39 kcal/mol, meaning it is thermodynamically favoured. Since it is suggested that this is the major product , clearly this reaction is thermodynamically controlled. It is also seen that the molecule 3 has a bending energy 6.86 kcal/mol larger than the molecule 4, which is pretty close to the difference in total energy (6.39 kcal/mol), suggesting this is the major contributor to the difference in total energies. This is due to the position of a double bond, where a dihedral angle in Molecule 4 (112.7^o) is closer to the stable 120^o conformation (sp²) than dihedral angle of molecule 3 (107.8^o), meaning Molecule 4 is thus less hindered and has a lower bending energy.

Stereochemistry of Nucleophilic Additions to a Pyridinium Ring (NAD+ analogue)

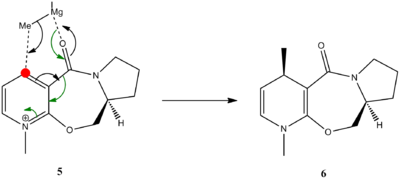
Reaction between derivative of prolinol (N-Methyl Pyridoxazepinone) and Grignard reagent (MeMgI)

In this reaction, molecule 5 reacts with a Grignard reagent, forming product 6. This reaction goes via nucleophilic addition where magnesium coordinates to the electronegative carbonyl oxygen and methyl group, which asks as a nucleophile, attacks the carbon (in red ). It was reported that this reaction is regio- and enantioselective.[6]

Figure 4:Reaction Mechanism of Molecule 5 to Molecule 6

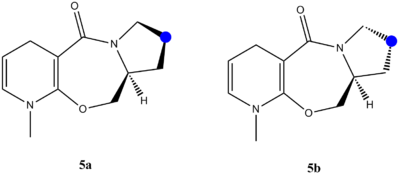
When optimising a molecule, it was found that there are two possible conformations for a 5 membered ring on prolinol. Carbon in blue

can either be up or down.

Figure 5: Molecule 5 (prolinol) showing -up- 5a and -down- 5b conformations

aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa

Table 3: Relative Energies of Molecules 5a and 5b

	Energies/ kcal mol-1
	Stretch	Bend	Stretch-Bend	Torsion	Van der Waals	Dipole-Dipole	Charge-Dipole	Total
Molecule 5a	1.19	7.41	0.09	14.44	16.17	2.83	-3.81	36.05
Molecule 5b	1.81	14.36	0.12	5.13	16.59	1.69	-3.99	35.11

It can be seen that the molecule with -down- conformation is more stable and is thus used in further optimisations and calculations. Interestingly, there are two big differences between the two molecules - bend and torsion energies. Bend energy is larger for a 5b molecule than 5a molecule (about 2x) but torsion energy is almost 3x smaller, suggesting there is less strain and this conformation is preferable.

Since it was reported that ChemBio3D 12.0 has a bug that affects the molecular mechanics force field when applied to molecules with N+ atom, different dihedral angles between a carbonyl carbon, carbon next to it and a carbon in red (Figure 4), have been studied in order to see if a minimum energy truly is obtained using MM2 optimisation.

Figure 6:Graph representing relationship between dihedral angle and total energy of the molecule 5b

Table 4: Total energies of Molecule 5b relative to dihedral angle

Dihedral Angles/o
	Total Energy /kcal mol-1
0	35.80
2	35.59
4	35.41
6	35.24
8	35.15
11	35.11
12	35.12
14	35.18
16	35.29
18	35.43
20	35.64

Dihedral angle at which the lowest energy was obtained is +11°. The positive sign means the carbonyl group lies above the plane of the pyridine ring and points forward (Jmol representation in Figure 5). Interestingly, when comparing energies of the molecule at dihedral angle -20 and +20, it has a higher energy at negative angle. This is another proof of how favourable it is for carbonyl group to be pointing above the plane, avoiding electronic clashes with other atoms. As mentioned before, since there was supposed to be a bug, so a non-mechanics method PM6 was performed as a reference. Note that the Grignard reagent could not be included in the structure since magnesium is not recognised by the in ChemBio3D.

Table 5: Total energies of Molecules 5a and 5b using PM6 method and the dihedral angle of molecule 5b

Structure
	Heat of formation in kcalmol-1 using MOPAC/PM6	Dihedral angle of molecule 5b at lowest energy
5a	93.69	-
5b	93.91	25.53

Even though the dihedral angles are different, all the energies are positive, despite different methods, meaning the carbonyl group truly is above the plane of the pyridine.

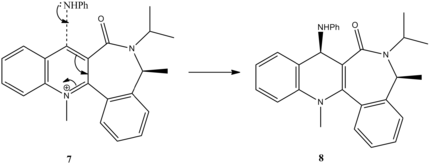
Reaction between aniline and PhNH2

The reaction below also proceeds via nucleophilic addition, however this time there is no coordination of NH₂Ph to the carbonyl because NH₂Ph is electron rich, which would cause a slight repulsion with the electronegative C=O group.

Figure 7:Reaction Mechanism of Molecule 7 to Molecule 8

Similarly, energies with different dihedral angles were studied with MM2 and PM6 optimisations.

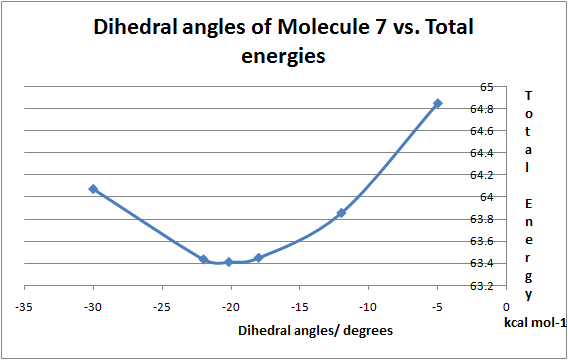
Figure 8: Graph of dihedral angles vs. total energies of Molecule 7 by MM2 optimisation

Table 6: Comparison of dihedral angles and energies for Molecule 7 with different methods

Method
	Dihedral Angle/°	Lowest Energy kcal/mol
MM2	-18.90	63.40
MOPAC/PM6	-43.69	156.19

On the contrary to the previous example, this reaction gives a total minimum energy at negative dihedral angle values, meaning the carbonyl is on the bottom face of the molecule 7. This is explained by the lone pair repulsion phenomenon. Since nucleophile contains a lone pair on the N atom, the phenylamine wants to avoid the bottom of the molecule in order to avoid repulsion, which results in amine being on the top face to give the molecule 8. This agrees well with the literature, where the site of nucleophile attack is on the opposite side of the C=O group due to sterics.

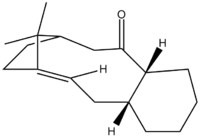
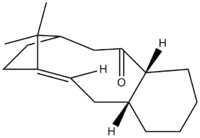
Stereochemistry and Reactivity of Intermediate in Synthesis of Taxol

When synthesising an important anti-cancer drug - Taxol, there is a key intermediate, either 9 or 10 (Figure 9) . This was proposed by Paquette where oxygen is either pointing up (9) or down (10). On standing though, the compound isomerises between the two, which is described as atropoisomerism. Their properties were again studied in ChemBio3D, where MM2 and MMFF94 optimisations were produced in order to see which isomer is more stable.

Figure 9: Possible intermediate 9 or 10 in Taxol synthesis

Since both molecules have a six-membered ring, the idea of boat/chair conformation has to be taken into account. In most occasions, a chair conformation is more stable that a boat. In order to see if this is true, both boat and chair conformations of the ring were examined, to obtain the structure with the lowest energy. At first, the optimisation gave a boat conformation, which was then manually dragged into a chair conformation and optimised again to yield a different energy. The optimised structures of both intermediates (9 and 10) can be seen below:

Table 7: Relative Energies of Intermediates 9 and 10 obtained by MM2 optimisation

	Energies/ kcal mol-1
	Stretch	Bend	Stretch-Bend	Torsion	Van der Waals	Dipole-Dipole	Total
Intermediate 9 - boat	2.77	16.57	0.46	20.65	14.05	0.18	54.23
Intermediate 9 - chair	2.68	15.83	0.40	18.27	12.69	0.14	48.92
Intermediate 10 - boat	2.67	11.35	0.31	21.73	13.57	-0.19	48.19
Intermediate 10 - chair	2.54	10.71	0.32	19.72	12.56	-0.18	44.28

Looking at the Table above, it can be seen that the theory of chair conformation being more stable than boat was confirmed. From both methods, MM2 and MMFF94, it was proven that the intermediate 10 is more stable (lower in energy by 4.64 kcal/mol (MM2) and 9.99 kcal/mol (MMFF94) ) than intermediate 9. This can be explained by looking at the carbonyl group and the hydrogens, shown in the Figure 9. When a carbonyl group is pointing upwards, there is a steric hindrance with the hydrogens, thus the higher energy. So the molecule prefers having a carbonyl group pointing downwards so the sterics is avoided. This agrees with the experimental observation, confirming the computed values.

Table 8: Relative Energies of Intermediates 9 and 10 obtained by MMFF94 optimisation

	Energies/ kcal mol-1
	Total
Intermediate 9 - boat	77.92
Intermediate 9 - chair	70.55
Intermediate 10 - boat	66.31
Intermediate 10 - chair	60.56

It is clearly seen that MMFF94 gives higher total energy, however trend still applies and shows which conformation is more stable. The reason in higher energy is due to different description of the non-bonded interactions.

As molecules ‘’’9’’’ and ‘’10’’’ are reported to react slowly, the energies were compared to the corresponding alkanes as it was stated that Taxol is a hyperstable alkene. Hyperstable alkenes are unreactive, containing less strain and results in negative strain energy. [11]. One way of relieving this strain in alkenes is by increasing the ring size, that is why a double bond in intermediates ‘’’9’’’ and ‘’’10’’’ is in 10-membered ring rather than heptane. However, the unreactivity itself is due to the a particular stability of the cage structure of the alkene rather than sterics as one might think. Thus, MM2 calculations were carried out on intermediates where a double bond is substituted with a single bond. This gave excellent results, proving the alkene olefin is more stable.

Table 9: Comparison of Intermediates - single bond substitution

	Energies/ kcal mol-1
Intermediate 9 - chair	48.89
Intermediate 9 - alkane - chair	53.69
Intermediate 10 - chair	44.29
Intermediate 10 - alkane - chair	54.52

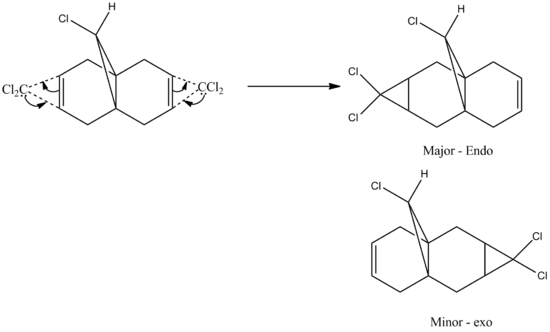
Regioselective Addition of Dichlorocarbene

Part 1: Orbital control

The reaction between 12 and dichlorocarbene yields an addition of CCl2 to the syn/endo C=C bond (double bond closer to Cl) resulting in this endo product being the major one and addition to the anti/exo double gives the minor product (72:23, respectively).

Figure 10: Reaction mechanism between 12 and dichlorocarbene yielding endo and exo Products

At first, PM6 method was used in order to obtain orbitals, however the orbitals were non symmetrical (despite molecule being C_s symmetry) so another method was tried - RM1 - which gave good results:

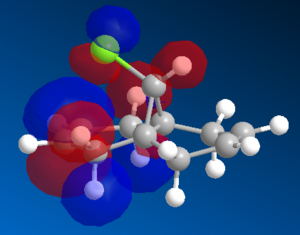
Figure 11: HOMO and HOMO-1 orbitals of 12 molecule using RM1 method

HOMO1	HOMO-1

Looking at the HOMO (left) it can be seen that electron clouds are mainly on syn/endo C=C bond, meaning this side is more susceptible to electrophilic attack. Looking at HOMO-1 (right) it too has electron clouds on syn but in addition has some electron density at anti C=C bond as well. This can be explained with π orbitals. Stabilisation of the exo π orbital is probably due to the orbitals having the right orientation to interact. Due to electronegativity of Cl atom, the πC-C is a high lying (filled) orbital and the σ*C-Cl is a low lying (empty) orbital. That is why the exo π orbital is more stable and consequently more electrophilic, so the nucleophilic attack thus happens at the endo π orbital (producing major product).

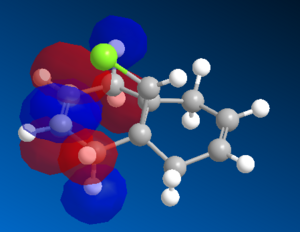
Figure 12: LUMO, LUMO+1 and LUMO+2 orbitals of 12 molecule

LUMO	LUMO+1	LUMO+2

Part 2: Vibrational frequency

Further analysis was done (MOPAC/RM1 method) on the two molecules 12 and 13 by examining vibrational frequencies.

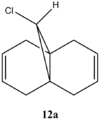
Figure 13: Molecules 12a and 12b

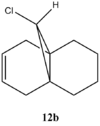Table 10: Comparison of stretching vibrational frequencies of 12a and 12b with included literature values

	12a	12b	Literature
IR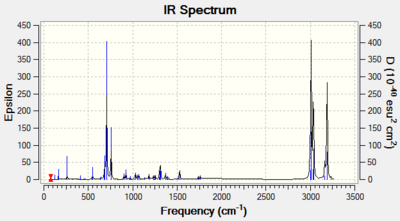
C=C (endo)/ cm-1	1757.35	1753.74	1745
C=C (exo)/ cm-1	1737.09	-	1745
C-Cl/ cm-1	770.83	779.98	760-505

Note that for molecule 12b only one C=C stretch is observed due to only one double bond which is endo to the C-Cl. This bond is not capable of overlaping with the C-Cl σ* and thus is not observed (no secondary orbital overlap).

There are three most important stretches for the two molecules: C-Cl and C=C endo and exo. All stretches correspond nicely to the literature, confirming the right conformation with lowest energies. It is interesting to see the shift of cyclohexene due to an electron withdrawing group – Cl. Normally, cyclohexene has a C=C stretch at 1645cm^-1, however in this case, due to chlorine, stretching frequency is higher – 1745 cm^-1. This effect can also be seen for endo and exo C=C stretches. Endo, is much closer to the chlorine than exo, therefore it is expected that its stretching is higher. This is in fact observed, giving frequencies of 1757.35cm^-1 and 1753.74cm^-1 for molecule 12a and 12b, respectively. For exo product, as expected, frequency of stretching is smaller - 1737.09 cm^-1 because π electron density is donated into the σ* bond resulting in delocalisation of orbintal and thus weaker bond (lower frequency). This is why, hydrogenation occurs at the exo C=C bond.

Structure-Based Mini-Project:

There were 3 different reactions that were studied, however none of them gave good results, i.e. did not agree with literature. Unfortunately, due to lack of time, a given reaction had to be studied and analysed.

Assigning Regisomers in Click Chemistry

Note that original paper had R₁=R₂=Ph, so Ph is used in these calculations as well.

Figure 14: Reaction mechanism

aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaa

Table 11: Relative Energies of two isomers, using MM2 method

	Energies/ kcal mol-1
	Stretch	Bend	Stretch-Bend	Torsion	Van der Waals	Charge-Dipole	Total
1,2-product	1.15	17.11	0.08	-15.66	14.78	-1.48	17.50
1,3-product	0.80	13.23	-0.02	-14.77	14.78	-1.45	11.07

It can be seen that the 1,3 dimer is more stable. This is due to having lower bend-energy (13.88 kcal/mol less), meaning there is less strain in the molecule and this conformation is preferred.

NMR analysis

¹³C NMR analysis for 1,2-isomer

Experimental/ ppm
	Literature/ ppm
55.83	51.85
127.93	126.93
128.01	127.22
128.25	128.22
128.97	128.92
129.58	129.08
129.21	129.64
131.29	133.26
133.87	133.34
135.42	135.66
138.77	135.66

(http://hdl.handle.net/10042/to-742)

¹H NMR analysis for 1,2-isomer

Experimental/ ppm
	Literature/ ppm
5.50 (s, 2H)	5.54 (s, 2H)
7.00 (t, 2H, J= 3.2 Hz)	7.07 (t, 2H, J = 3.6 Hz)
7.19 - 7.25 (m, 5H)	7.23 – 7.27 (m, 5H)
7.38-7.53 (m, 3H)	7.37 – 7.46 (m, 3H)
7.71 (s, 1H)	7.73 (s, 1H)

¹³C NMR analysis for 1,3-isomer (Note that only graph for literature values was available, meaning ppm is less accurate).

Experimental/ ppm
	Literature/ ppm
55.24	~54
126.73	~126.93
74.30-77.21	~76.5-78
120.25	~119.5
128.11	~126
128.90-130.04	~128-129.5
129.02	~131
133.68	~135
147.54	~148

(http://hdl.handle.net/10042/to-7429)

¹H NMR analysis for 1,2-isomer

Experimental/ ppm
	Literature/ ppm
5.47 (s, 2H)	5.49 (s, 2H)
7.29 (m, 8H)	7.25 (m, 8H)
7.58 (s, 1H)	7.66(s, 1H)
7.77(d, 2H)	7.83 (d, 2H)

When IR spectra were compared, there were no major differences, so this was omitted from the results section. This is due to the fact that there are the same functional groups on both isomers, which gives similar stretches and this method would not be very good for distinguishing between the two.

Conclusion

It was learnt how molecular mechanics, semi-empirical molecular orbital theory and DFT-based molecular orbital methods work, how easy it is to perform essential calculations, which would not be possible without these programs. The main aims have thus been fulfilled. However, there is always one disadvantage of these methods. They are all run on the computer and the errors, bugs, etc. always persist and sometimes it is beyond our understanding. Overall, though, very useful techniques that worked on most of the molecules.

Molecular mechanics was used to optimise the molecule's geometry to an energy minimum, independently of reaction being kinetically controlled or thermodinamically controlled. Sometimes, one has to manually drag an atom into another position in order to obtain the lowest energy (just as cyclohexane chair - boat example), but nevertheless it gives good results. Why not excellent? Well, they do not really take into account electrons and orbitals effects which are often very important in considering the reactivity of bonds and spectroscopic properties. This was actually observed in regioselective addition of dichlorocarbene, where exo double bond undergoes hydrogenation due to endo double bond being more prone to electrophilic attack.

Unfortunately, due to lack of time, the Mini-Project was not discussed in-depth as it could have been. Since 3 other reactions were tested beforehand and did not work, this is another proof where these computational methods fail. They, sometimes, cannot take large molecules or heavy metals and so calculations will not work. However, all calculations were still performed on the chosen reaction and they gave rather excellent results compared to the literature.

Overall it can be concluded that this experiment was successful and very beneficial, especially in terms of dealing with problems that might have occurred during calculations. This gave even better understanding of the computational methods and how essential they are in Chemistry.