Rep:Mod:SaveMeSanFrancisco

Computational Labs - Module 3 (Physical Chemistry)

Author: Thomas McDevitt

Simple computational chemistry involves the iterative calculation of energetically minimised geometries of molecules. This can be done using MM2 molecular mechanics (purely a classical point of view) which utilizes Newtonian physics to calculate energies of molecules. This perspective cannot, however, be used to examine transition states due to its inability to describe the formation and destruction of chemical bonds, meaning that basic quantum mechanics need to be introduced to calculate molecular orbitals by solving the Schrödinger equation, generating a potential energy surface and hence finding appropriate transition structures.

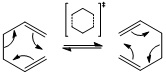
The Cope Rearrangement

This is an example of a pericyclic reaction (or, more specifically, a [3,3]-sigmatropic shift; an atom chain migration, where the numbers represent the length of the chain that migrates and the length of the backbone along which the chain migrates). Simple pericyclic reactions are ideal for the purposes of this module as they proceed through a concerted cyclic transition state as opposed to passing through a discrete intermediate in a stepwise reaction. The transition state in this particular example can either have a chair or a boat conformation.

The Cope rearrangement.

Optimised Structures and Energies of Products/Reactants

Various conformations of 1,5-hexadiene were drawn and optimised using a Hartree-Fock/3-21G method.

Structure	Conformation	Energy / a.u.	Point Group	Equivalent (Appendix 1)
Cyclopentadiene	Anti	-231.69260 (5.d.p.)	C2	Anti 1
Cyclopentadiene	Gauche	-231.68772 (5.d.p.)	C2	Gauche 1

The anti- conformation has a lower (more negative, in this case) energy than the gauche- conformation. This relates to the forces which render the eclipsed conformation of ethane higher in energy than the staggered conformation.

Staggered ethane.

Eclipsed ethane.

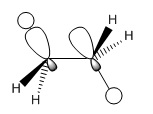
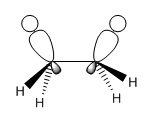
In staggered ethane, there is electron donation from any one σ-bonding orbital into the directly opposite σ-antibonding orbital, causing a mild degree of conjugation resulting in overall stabilisation of the molecule. This kind of interaction can occur in any antiperiplanar relationship, where the degree of stabilisation relates to the stability of the situation in the image below.

The eclipsed conformation, however, not only lacks this interaction but has another which destabilised the molecule, namely the interaction between two filled σ-bonding orbitals. Electron-electron repulsion raises the energy of the molecule.

The effective stabilisation of staggered ethane.

This, as such, explains why the conformer of 1,5-hexadiene with more staggered relationships is more stable than that with more eclipsed relationships. More specific to the molecule in question, a C-C σ-bond eclipses a C-C π-bond. However, when considering the most stable conformer, one must consider carefully how to apply this effect.

The two staggered conformations of 1,5-hexadiene.

To the left, the two staggered conformations of 1,5-hexadiene can be seen. The rotamer to the right, where the CHCH2 groups are antiperiplanar to each other, steric hindrance is at a minimum - however, since the groups are antiperiplanar to each other, the stabilisation above will relate to the formation of a CHCH2 carbocation and a CHCH2 carbanion, which is not ideal. In the situation to the left, where the two such groups are gauche with respect to each other, they are antiperiplanar to hydrogen groups which much more easily accommodate the stabilisation effected by the aforementioned σ-σ* interaction. This is the gauche effect and leads to the theoretically deduced hypothesis that the rotamer shown to the left will be the lowest energy conformation. This hypothesis can be tested.

Structure	Conformation	Energy / a.u.	Point Group	Equivalent (Appendix 1)
Cyclopentadiene	Fully Optimised	-231.69266 (5.d.p.)	C1	Gauche 3

The energy obtained is lower than both of the conformers trialled previously. It is worth noting that whilst the energy is lower, it is only 6x10_-5 a.u. lower than the anti- conformation. This shows that whilst the stereoelectronics dominate sterics, the amount which it is overcome is very low; they both play a significant part.

Calculating a Potential Energy Surface

A conformer similar to anti1 (namely, anti2) was drawn and optimised using the same method as before - the HF/3-21G method. This was then optimised again using a higher level of accuracy - a DFT optimisation at the B3LYP/6-31G(d) level. The energies obtained for both were then compared.

Structure	Conformation	Energy / a.u.	Point Group
Cyclopentadiene	Anti-2 (HF/3-21g)	-231.69254 (5.d.p.)	Ci
Cyclopentadiene	Anti-2 (DFT/B3YLP/6-31G(d)	-234.61171 (5.d.p.)	Ci

Whilst there are no major differences in the geometry, the energy obtained for the DFT method is lower than that obtained for the HF one. This may suggest that a more stable conformation has been obtained, though since energies measured are simply relative values as opposed to absolute energies, the energies obtained for two different methods cannot be directly compared as they were generated in different ways.

Something worth noting was that the HF calculation took 15 seconds, whereas the DFT took 1 minute and 15 seconds (5x as long), showing how the greater level of accuracy requires a significant amount more computational resources. For molecules much bigger than this, it becomes necessary to make do with a lower level of accuracy just to complete calculations in a feasible length of time.

To obtain a potential energy surface comparable to experimental values, one final scan was needed - a vibrational frequency scan. This was done, also using the DFT/B3YLP/6-31G(d) method.

The computer-generated IR Spectrum of the Anti-2 Conformer of 1,5-Hexadiene.

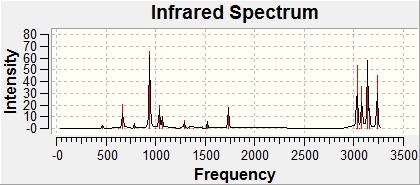
Once complete, the formatted checkpoint file was opened, and the vibrational frequencies observed to check for imaginary frequencies (of which there were none) and to inspect the generated infrared spectrum. After this, the log file was opened and the real-output examined for data regarding energies.

Key values were as follows:

 Sum of electronic and zero-point Energies=           -234.469196
 Sum of electronic and thermal Energies=              -234.461849
 Sum of electronic and thermal Enthalpies=            -234.460905
 Sum of electronic and thermal Free Energies=         -234.500777

C.f. Total energy of the molecule is -234.61171.
All energies here are given in atomic units.

These results are in good agreement with those calculated previously.

	Sum of electronic & zero-point energies / a.u.	Sum of electronic & thermal energies / a.u.
Calculated value	-234.46920	-234.46185
Provided value	-234.46920	-234.46186

Optimisation of the Chair Transition State

The optimised allyl fragment.

An allyl fragment (CH₂=CH-CH₂) fragment was drawn out into GaussView and optimised using the HF/3-21G level of theory. A transition structure was obtained, though it was found that the calculations would only converge to the expected transition structure if the fragment drawn at the beginning was planar. The optimised result was then copied and pasted twice into a new MolGroup to approximately represent chair-cyclohexane, with the terminal ends of the fragments approximately 2.2Å apart. This was the guess structure of the transition state and had to be adjusted to be as close as possible to the real transition structure for the optimisation to work.

The imaginary vibration of the optimised transition structure.

First Transition State Optimisation

This was then optimised to a transition state using an Opt+Freq option (to enable frequency analysis). Instead of being optimised to a minimum (as geometry optimisations would go), it was optimised to a transition state. Force constants would be calculated once. The resulting structure represented a typical cyclohexane boat type geometry. Its vibrations were analysed - there was an imaginary vibration at -817.98 cm^-1 (2.d.p) which is shown to the left. This vibration corresponds to the Cope rearrangement.

Second Transition State Optimisation - Frozen Coordinate Method

The optimisation was repeated from the guess structure. However, this time, the distances between terminal carbons of the allyl chains (with each one to their respective counterpart in terms of bond formation) were frozen to their existing bond lengths. The Optimisation + Frequency analysis was performed and the resulting structure resembled that obtained with the last method, given that the bond lengths had been frozen. There was also one imaginary frequency at -765.08 cm^-1 (2.d.p.) which had the same vibrational mode as that of the last optimisation. The bond lengths would be optimised this time, by using the redundant coordinate editor to add a bond between the appropriate terminal carbons and optimising the structure to a transition state without force constants. The resulting structure strongly resembled the result of the first optimisation, and had an imaginary frequency at -838.04 cm^-1. The two structures were then compared.

Comparison of the Two Optimisations

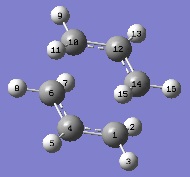The chair-transition structure with atom labels.	Atoms	Value (1st Optimisation)	Value (2nd Optimisation)
	C1-C4; C4-C6; C10-C12; C12-C14	1.38929Å	1.38930Å
	C1-H3; C6-H8; C10-H9; C14-H16	1.07600Å	107600Å
	C1-H2; C6-H7; C10-H11; C14-H15	1.07426Å	1.07423Å
	C4-H5; C12-H13	1.07585Å	1.07588Å

The two results agree almost identically, with the variations easily being put to error in the calculations (with the settings used, 3x10^-5 Å is well under the resolution of the calculations). The fact that two different methods have converged so well to the same result suggests that the result obtained for both methods is correct, as far as the underlying theory is concerned.

Optimisation of the Boat Transition State

For the optimisation of the boat structure, we will use a different method: the QST2 method. This involves manual specification of the products and reactants, and running a calculation to find an appropriate transition state. For this to work, both the products and reactants need to be drawn with identical atom labels (though obviously with different structures). The previously optimised Anti-2 structure was used twice in a single new MolGroup, the second copy of which was adjusted so that the atom labels would reflect those of the product. The resulting labels were as follows.

The anti-2 conformer with labels for both the reactant and product of the Cope rearrangement.

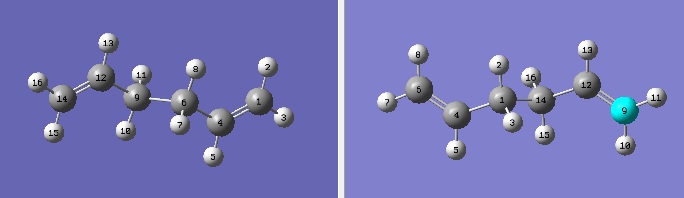
At this point, the first QST2 calculation was performed with an optimisation/frequency, optimising to a TS(QST2) (as opposed to TS(Berny) which had been used previously). The calculation was performed and the output formated checkpoint file examined, at which point it was noticed that the result showed a very unusual (and, by matter of simple chemical logic, incorrect) structure.

The failed calculation for the boat structure.

This was because the starting molecules for the calculation were so far from the intended boat structure that the calculation would never have reached the target transition state. As such, the molecules had to be adjusted.

• The dihedral angle between the central four carbon atoms for both molecules was set to 0^o.
• The angles for the inside C-C-C bonds (e.g. C₆-C₉-C₁₂ in the molecule above to the left) were reduced to 100^o.

The resulting structures appeared as follows.

The adjusted starting structures for the boat transition state structure calculation.

Cyclopentadiene

The new boat transition state - a successful calculation.

The imaginary vibration in the boat transition structure.

The calculation was rerun. As expected, the resultant molecule was a transition state shaped as a cyclohexane boat. The frequencies were analysed - the structure was found to have a single imaginary frequency at cm^-1 which has been animated to the right (c.f. that of the chair transition state structure of cm^-1). Note - the rotatable Jmol files aren't saved with enough data to effectively display the transition state bond behavior in an endeavor to save disk space.

Comparison of Boat and Chair Transition Structures

Cyclopentadiene

The IRC (Intrinsic Reaction Coordinate) method will now be used to determine the conformation of the products of the minimum energy path from each transition structure on a potential energy surface. The first optimised structure from the chair transition structure calculations was used, and scanned using Gaussian with an IRC method, recalculating the force constants at every step with an additional 50 steps to ensure reliability of the outcome. The calculation, incidently, took a lot longer than most others (just under 4 minutes on the Imperial College SCAN system, whereas most of the other calculations had taken less than 30 seconds). The resulting formatted checkpoint file had 47 molecules in it - the last of which shows the product conformation. It is shown to the right as a rotatable Jmol. Its geometry represents most well that of the Gauche-2 conformation, and incidently had a very similar energy - its total energy was -231.69165 a.u. (c.f. Gauche 2, which has a total energy of -231.69167 a.u.).

Cyclopentadiene

This process was then repeated in an identical manner with the final geometry for the boat transition structure. The final structure obtained is shown to the left. It has an energy of -231.68301 a.u. (5.d.p.), one of the much higher energy conformers of 1,5-hexadiene (and higher than all of those shown in Appendix 1), which can be justified by noticing the eclipsed nature of all of the entities whilst rotating it such that one is looking directly down the central C-C bond.

These results are justifyable in the sense that a lower energy (more stable) transition state gives rise to a more stable conformer (the chair-shaped transition state gives rise to the gauche-2 conformer of 1,5-hexadiene) whereas the higher energy (less stable boat-shaped TS) produces a much higher energy conformer. This suggests that, whilst the Cope rearrangement could potentially occur through a boat-transition state structure, but its higher energy will cause it to occur a lot less.

Activation Energy Calculation

The final product calculated with the IRC method is exactly the same as the reagent (the reaction coordinate is symmetrical) hence the difference in energy between the transition state and the calculated product is the activation energy. There are 4 obtained structures in question - the boat and chair transition states and their respective products/reagents. All of these have calculated energies in atomic units at the Hartree-Fock/3-21G level. They will also be calculated at the DFT/B3YLP/6-31G(d) level.

	Boat Product	Boat TS	Chair Product	Chair TS
Energy / a.u. (HF)	-231.68301	-231.60280	-231.69164	-231.61932
A. Energy / a.u.	0.08021		45.4
A. Energy / kcal mol-1	50.3		0.07232
Energy / a.u. (DFT)	-234.60311	-234.54309	-234.61068	-234.55698
A. Energy / a.u.	0.06002		0.05370
A. Energy / kcal mol-1	37.7		33.7
A. Energy / kcal mol-1 (Exp)	44.7		33.5

Here, 1 hartree = 627.509 kcal mol^-1.

Despite computational error, the calculations haven't brought a figure for the activation energy that agrees very solidly with experimental figures. However, they do help to give a good idea of the relative activation energies and lead to the conclusion (as can be backed up by theory) that the boat transition states are higher in energy and are more difficult to attain.

The Diels-Alder Reaction

The Diels-Alder cycloaddition is a specific kind of pericyclic reaction that occurs between a dienophile and a diene to form a single unsaturated group. In this section of the module, the transition states of the Diels-Alder reactions will be analysed (as well as their molecular orbitals inspected) in the reactions between cis-butadiene and ethylene, and then between cyclohexa-1,3-diene and maleic anhydride.

The Diels-Alder Reaction of Cis-Butadiene and Ethylene

The Reagents

• Cis-butadiene optimisation on D-Space: DOI:10042/to-6294
• Ethene optimisation on D-Space: DOI:10042/to-6302

Cis-Butadiene was optimised using the HF/3-21G level of accuracy. The molecular orbitals were then examined and the HOMO/LUMO plotted.

The HOMO of cis-butadiene.

The LUMO of cis-butadiene.

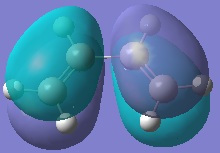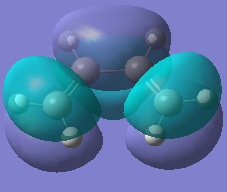It can be seen that the HOMO is antisymmetry but the LUMO is symmetric with respect to the plane of symmetry in the molecule (σ_v as opposed to σ_h).

Ethene was drawn into Gaussview and optimised. The HOMO and LUMO for this were then plotted and the symmetry inspected.

The HOMO of ethene.

The LUMO of ethene.

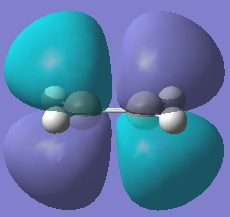This time, the HOMO is symmetric whereas the LUMO is antisymmetric with respect to the plane of symmetry of the molecule (more specifically, the σ_v plane that bisects the π-bond).

The Product

• Cyclohexene optimisation on D-Space: DOI:10042/to-6301

The product was then drawn out. As can be seen from the reaction scheme, the product for this particular Diels-Alder reaction is cyclohexene.

The Diels-Alder reaction between cis-butadiene and ethylene.

The product in this case is cyclohexene. It can be seen that the reaction will only proceed forward to form cyclohexene if the butadiene is in its cisoid-conformer, hence when butadiene is drawn out, it is drawn out as cis-butadiene and optimised as such, despite it not necessarily being the lowest energy conformation.

The Transition State

• Transition State calculation on D-Space: DOI:10042/to-6303

The cis-butadiene and ethene were put together in one molecule window whereas in a second molecule window within the same MolGroup, the cyclohexene was pasted. The atoms were numbered identically and then a QST2 scan was performed.

The numbering of atoms between products and reactants.

Cyclopentadiene

The vibration corresponding to this Diels-Alder reaction.

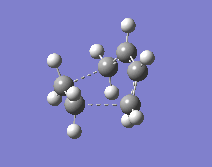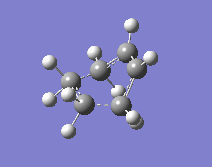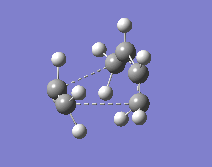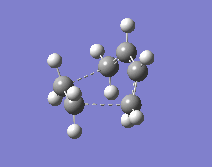
One thing that had to be considered was the suprafacial disrotation of the terminal CH₂ groups in the cis-butadiene. For a heat-initiated 6-electron (4_π+2_π) pericyclic cycloaddition, these groups turn in opposite directions and this has to be taken into account when numbering the atoms (another thing worth noting is that this 6-electron pericyclic reaction, when initiated by heat, will proceed through a Hückel transition state). A QST2 calculation was then performed to optimise and calculate frequencies.

The transition state obtained is shown to the right. This shows the attack of the ethene on the cis-butadiene at and angle above the plane it occupies.

Upon inspection of the frequencies, one imaginary frequency was calculated at -819 cm^-1 which was found to be the frequency corresponding to the cyclisation in question. This imaginary frequency is shown to the left.

The molecular orbitals of this transition state were analysed.

The HOMO of the transition state.

The LUMO of the transition state (the "face").

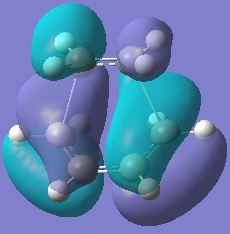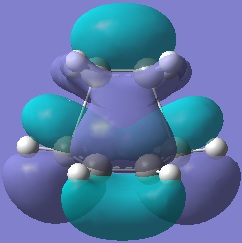The HOMO is antisymmetric with respect to the plane of symmetry of the molecule in question whereas the LUMO is symmetric.

Structural Analysis of the Transition State

The structure of the transition state was examined in closer detail to determine some of its properties.

C---C (bond being formed) length: 2.20Å, C.f.:

• Cyclohexane: 1.53Å
• Benzene: 1.40
• Propene: 1.34Å

The Van-der Waals radius of carbon is 1.30Å, suggesting that the bond has not completely formed due to its much higher length (c.f. those of a standard comparable C-C single bond, C=C double bond, or C=C aromatic bond - comparable as this is a Hückel transition state). The formation of the bond occurs when the filled antisymmetric HOMO of cis-butadiene interacts with the unfilled antisymmetric LUMO of ethene, and the filled symmetric HOMO of ethene interacts with the unfilled symmetric LUMO of cis-butadiene, leading to a transition state with an antisymemtric HOMO and a symmetric LUMO.

These bonds form in a synchronous manner as can be seen from the imaginary vibration. The terminal carbons of both cis-butadiene and ethene approach each other at exactly the same time - which corresponds to the earlier statement that the formation and destruction of bonds in a pericyclic reaction has to be concerted.

The Diels-Alder Reaction between Cyclohexa-1,3-diene and Maleic Anhydride

This reaction has to be considered carefully in that there are two products - the exo- isomer and the endo- isomer. The endo isomer is preferentially formed, but each will be explored in terms of the energies of the final products and energies of their respective transition states to see if this can be rationalised using computational data and chemical intuition.

The Reagents

• Cyclohexa-1,3-diene optimisation on D-space: DOI:10042/to-6323
• Maleic Anhydride Optimisation: DOI:10042/to-6324 </ul
  Cyclohexa-1,3-diene was drawn into Gaussview and optimised at the HF/3-21G level. The same was done for maleic anhydride. Since the reagents for both outcomes of this reaction are identical, this part of the examination only needs to be performed once. The molecular orbitals (namely, once again, the HOMO/LUMO) were examined.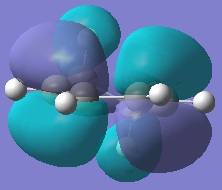
  
  

  The HOMO of cyclohexa-1,3-diene.

  The LUMO of cyclohexa-1,3-diene.

  
  Here, the HOMO is antisymmetric and the LUMO is symemtric. It seen on these images that should the molecule be rotated with in exactly the opposite way, the HOMO would be symmetric about a C₂ axis that goes orthogonally to the plane that the molecule is being viewed in, and similarly the LUMO would be antisymemtric through this same axis. However, since this is the diene in our Diels-Alder reaction, we are only looking at the reactivity of, and hence electron density of, the π-bonds which will react with the dienophile.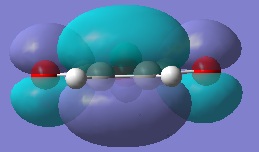
  
  

  The HOMO of maleic anhydride.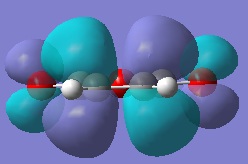

  The LUMO of maleic anhydride.

  
  The HOMO of maleic anhydride is symmetric with respect to the σ_h plane of symmetry, and the LUMO is antisymmetric with respect to this same plane.
  
  

  The Products

  • Exo-product optimisation on D-Space (first): {{DOI|10042/to-6327
  • Endo-product optimisation on D-Space (first): {{DOI|10042/to-6328
  
  The endo- and exo- products were then drawn out and optimised separately. After the first optimisation at the HF/3-21G level of accuracy, the molecules appeared to have a lot less symmetry than expected, so a second optimisation was done at the DFT/B3YLP/6-31G level.
  
  

  References and Citations