Rep:Mod:Salvatore89
The hydrogenation of Cyclopentadiene dimer
The dimerisation of cyclopentadiene is a typical example of a reaction subject to the endo rule. In general periyciclic reactions can be only understood by careful consideration of the stereolectronic properties of the molecules. The dimerisation of cyclopentadiene favours the formation of the thermodynamically less stable ''endo'' product. However under equilibrating conditions the ''exo'' product becomes dominant, for this reason old solutions of Cp consist mainly of the exo adduct and the dimer needs to be cracked to obtain the endo adduct.[1] At this point it is worth explaining briefly the difference between kinetic and thermodynamic control:
- Under thermodynamic control the reaction is reversible and equilibrium is established between the starting material and the product, in this case the most stable product predominates.
- Under kinetic control the reaction is irreversible and the transition state barrier can only be crossed in the forward direction, for this reason the most rapidly formed product predominates; this is generally the one obtained by crossing the lowest activation energy barrier.
In the following calculations has been determined the overall energy of the two adducts by a Molecular Mechanics technique. Specifically the parameters for the following molecule were obtained by minimizing the energy of the molecule using the Allinger MM2 molecular mechanics model.
exo-Cyclopentadiene dimer endo-Cyclopentadiene dimer
Stretch: 1.2855 1.2511 Bend: 20.5794 20.8483 Stretch-Bend: -0.8381 -0.8357 Torsion: 7.6571 9.5105 Non-1,4 VDW: -1.4171 -1.5431 1,4 VDW: 4.2322 4.3189 Dipole/Dipole: 0.3776 0.4475 Total Energy: 31.8766 kcal/mol 33.9975 kcal/mol
The product that is lowest in energy is the exo-product. Molecular mechanics is sufficient for the estimation of the most stable product as steric factors are predominant in determining the stability of these molecules and more advanced quantum mechanical calculations would not give a qualitatively different answer. In order to prove this point the structures for the two molecules were optimized by semi empirical molecular orbitals methods PM6 and the results obtained followed the expected trend: endo adduct energy = 41.91829 Kcal/Mol > exo adduct energy = 40.47366 Kcal/Mol.
An attempt to calculate the structure and the vibration frquencies of the transition state for the formation of the endo-cyclopentadiene dimer was carried out. The structure of the reaction intermediate was first optimized by semi empirical PM6 method and subsequently the structure was optimized again for the transition state by Density Functional Theory calcualations. Surprisingly the results obtained resembled the transition state of a Cope rearrangement which is generally believed to be one of the possible routes for this dimerisation. The structure obtained from the calculation can be observed here Transition State . Analysis of the vibrational frequencies shows the expected negative vibration frequency corresponding to the imaginary frequency of crossing the activation barrier. The negative vibration is calculated at -546cm-1 and corresponds to the vibration of the forming bond (where the not formally bonded hydrogen can be seen). The overall energy of the TS is found to be -388.12a.u., however it would have been necessary to scan a large number of possible transition states to identify the lowest in energy.
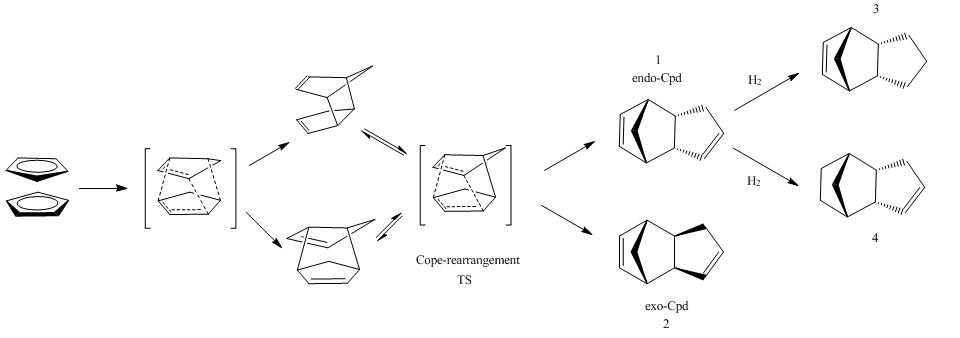
Analogous molecular mechanics calculations were performed in order to calculate the ease of hydrogenation of the kinetically favoured endo product. We will denominate the endo cyclopentadiene dimer hydrogenated at the dienophile ring as endo-Cpd-3 while the one hydrogenated at the dienophilic ring as endo-Cpd-4. The results are shown below:
hydrogenated endo-Cyclopentadiene dimer-3 hydrogenated endo-Cyclopentadiene dimer-4
Stretch: 1.2773 1.0965 Bend: 19.8622 14.5248 Stretch-Bend: -0.8346 -0.5493 Torsion: 10.8081 12.4972 Non-1,4 VDW: -1.2229 -1.0701 1,4 VDW: 5.6330 4.5124 Dipole/Dipole: 0.1621 0.1406 Total Energy: 35.6850 kcal/mol 31.1520 kcal/mol
In terms of the overall stability the endo-Cpd-3 is found to be higher in energy that the endo-Cpd-4. The major contribution to this difference in energy can be found by analyzing the deviations from ideality of the single parameters specified above. It appears immediately obvious that the largest difference lies in the deviation from bond angles ideality (Bends) which is considerably larger for the endo-Cpd-3; so does the bond length and the VdW interactions. On the other end the endo-Cpd-3 is less torsionally stressed than the endo-Cpd-4. To give a more exact and quantitative picture of where the major components of strain lie, the deviation from ideality of bond angles were calcualted and the major contributions to non ideality follow in the table. To identify the angles refer to the structures endo-Cpd-3 and endo-Cpd-4
hydrogenated endo-Cyclopentadiene dimer-3 hydrogenated endo-Cyclopentadiene dimer-4 Angle Calc. ideal Δ-angles Angle Calc. ideal Δ-angles C(4)-C(7)-C(3) 93.6861 109.5 15.8139 C(4)-C(7)-C(3) 92.5919 109.5 16.9081 C(4)-C(1)-C(2) 107.766 122.0 14.234 C(9)-C(10)-C(6) 112.4331 122.0 9.5669 C(3)-C(2)-C(1) 107.767 122.0 14.2322 C(10)-C(9)-C(8) 113.0453 122.0 8.9547 C(7)-C(4)-C(1) 97.938 109.5 11.5715 C(7)-C(3)-C(5) 100.8147 109.5 8.6953 C(7)-C(3)-C(2) 97.938 109.5 11.5712 C(7)-C(4)-C(1) 101.1453 109.5 8.3647 C(7)-C(4)-C(6) 100.078 109.5 9.4313 C(7)-C(3)-C(2) 101.2139 109.5 8.2961 C(7)-C(3)-C(5) 100.079 109.5 9.431 C(8)-C(5)-C(3) 117.7888 109.5 8.2788 C(8)-C(5)-C(3) 117.872 109.5 8.362 C(7)-C(4)-C(6) 101.6222 109.5 7.8878 C(10)-C(6)-C(4) 117.871 109.5 8.3614 C(6)-C(5)-C(3) 101.9052 109.5 7.6048
- ↑ Inan Fleming, Molecular Orbitals and Organic Chemical Reactions, Wiley 2010
Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol
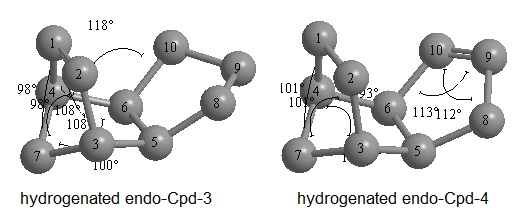
A key intermediate in the synthesis of the anti-cancer drug Paclitaxel (sold under the trademark TAXOL) shows an interesting type of isomerism named atropisomerism. Atropisomeric compounds possess chirality not for the presence of a stereogenic centre but because their rotation around one bond is restrained to such an extent to allow for the isolation of two conformers at room temperature. In the particular case of the TAXOL intermediate the interconversion for the ring configuration is restrained yielding to possible atropoisomers, one that has the carbonyl oxygen pointing above the plane of the molecule and the other pointing below. Relative stabilities for the two isomers have been calculated by Alliger MM2 molecualar mechanics and Merk Molecular Force Fields MMFF94 methods and the results obtained follow:
Carbonyl up MM2 Carbonyl down MM2
Stretch: 2.7844 2.6194 Bend: 16.540 11.340 Stretch-Bend: 0.4300 0.3430 Torsion: 18.255 19.672 Non-1,4 VDW: -1.5543 -2.1621 1,4 VDW: 13.110 12.872 Dipole/Dipole: -1.7251 -2.0019 Total Energy: 47.840 kcal/mol 42.683 kcal/mol
Carbonyl up MMFF94 Carbonyl down MMFF94
Final Energy: 70.528 kcal/mol 66.278 kcal/mol
The results for the two methods are qualitatively and quantitatively similar in fact they both yield a energy difference of about 5 kcal/mol. (By assuming that we can estimate the thermal energy difference between the two conformers using the equations valid for the kinetic model of an ideal gas we say...)Knowledge of which intermediate is most stable is extremely important when planning a synthetic route as each conformer will yield a different product when reacting at the carbonyl group.
A careful observation of the structure of both conformers will suggest the reason why these molecules show great stability towards functionalisation of the olefinic bond: the left hand side of these molecules as it can be seen in the representation above constitutes a bicyclic system with one of the sp2 carbons being a bridgehead. Bredt's rule[1] asserts that double bonds tend to avoid ring junctions however these rules can be clearly violated as the molecules we are considering fall in this class. Numerous qualitative studies were conducted on the applicability of Bredt's rule and bridgehead olefins until Maier and Schleyer [2] conducted a thorough quantitative analysis of this class of compounds by Allinger MM1 force field calculations and identified a new class of "hyperstable" olefins which contain less strain than the parent hydrocarbon and have negative OS(olefin strain) values. They explain that such olefins should be very unreactive not due to steric hindrance or enhanced π-bond strength but due to special stability afforded by the cage structure of the olefin and to the greater strain of the parent polycycloalkane. The great difference in stability between the polycycloalkane and the bridgehead alkene can be easily computed by MM2 force field calculations. The results obtained for the hydrogenated species were
Carbonyl up Carbonyl down
Stretch: 4.3349 cf.2.7844 7.0142 cf.2.6194 Bend: 21.460 cf.16.540 86.014 cf.11.340 Stretch-Bend: 0.9781 -0.0936 Torsion: 22.562 cf.18.255 18.931 cf.19.672 Non-1,4 VDW: 1.5883 2.6967 1,4 VDW: 17.165 -2.6051 Dipole/Dipole: -1.7361 -2.6051 Total Energy: 66.352 cf.47.840 144.23 cf.42.683 kcal/mol
The hydrogenation reactions are strongly endothermic, particularly for the intermediate with the carbonyl oxygen pointing down and as predicted by Mayer and Schleyer the major contribution come from the considerably increased deviation from ideality in the bond angles the overall torsion of the molecules and the bond lengths. The strong endothermicity of these reaction explains the very slow rate of reaction for the functionalisation of these class of molecules.
- ↑ Bredt, J.; Thouet, H.; Schmitz, J. Liebigs Ann. Chem. 1924, 437, 1.
- ↑ Wilhelm F. Maier, Paul Von Rague Schleyer, J. Am. Chem. Soc., 1981, 103, 1891. DOI: 10.1021/ja00398a003
Regioselective addition of dichlorocarbene
The stereoselctive reactivity of π-faces towards nucleophiles and electrophiles caused much interest in the past. 9-Chloro-1,4,5,8-tetrahydro-4a,8a-methanonaphtalene (we will refer to it simply as diene)showed to react stereospecifically only at the double bond syn to the Chlorine. This system was thoroughly studied by Halton, Boese and Rzepa[1] who rationalized the stereoselectivity in terms of molecular orbitals interaction. Their results were also confirmed by determination of the crystal structure of the diene in question that, at a qualitative level of accuracy, showed the same ring deformations predicted by the MOPAC PM3 calculations.
MOPAC PM6 calculations were conducted on the diene in order to justify the regioselectivity of the diene. Contrarily to the molecular mechanics force fields calculations conducted before, in order to explain the reactivity of the diene a quantum mechanical approach is necessary. For this purpose molecular orbital semi empirical calculations PM6 were conducted on the diene and the frontier orbitals were identified.
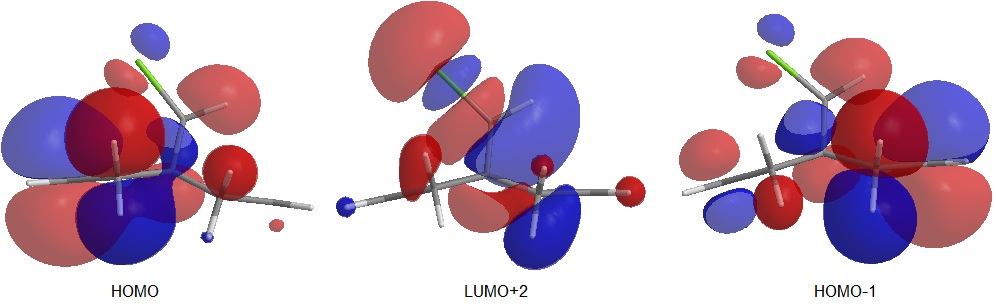
The results obtained are in line with the ones reported in the literature. It can be immediately noticed that the HOMO is localized on the alkene syn to the chlorine making the endo alkene more nucleophilic in terms of frontier orbitals. In fact an electrophile will interact with the HOMO electrons which are the highest in energy and hence the most polarisable. It should be noted that the calculated molecular orbitals are fully symmetrical as the molecule is overall Cs in symmetry which is equivalent to describing it as having a plane of symmetry groing through the C-Cl double bond.
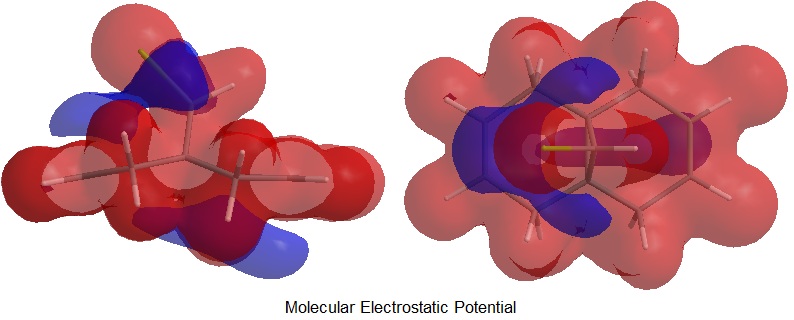
As well as frontier orbitals, the stereoselectivity of this rigid diene, free from any differentiating steric moiety, could be also due to asymmetry of the molecular electrostatic potential (MEP) as proposed by ref.[1]. In line with the literature the PM6 MEP calculation suggested electrostatic π-facial asymmetry (in the figure above the negative potential is represented in blue). This feature is most likely due to an antiperiplanar stabilizing interaction between the occupied anti π*-orbital, shown above as HOMO-1, and the C-Cl σ*-orbital, shown above as LUMO+2.
The vibrational frequencies for the diene and a hydrogenated diene with only the syn-olefin were calculated by density functional theory B3LYP/6-31G(d,p) Gaussian geometry optimization and frequency calculation. The DFT is a form of ab-initio calculation and unlike MOPAC does not use any empirical parameter in the determination of the molecular orbitals and properties of a molecule. This also means that the computational demand for this approach is considerably higher than for force field or semi empirical methods.
Structure optimization and calculation of the vibrational spectrum yielded the following results for the C-Cl bond and for the olefinic bonds:
Diene Hydrogenated Diene
v Intensity v Intensity
C-Cl 770.8 25.15 778 20.02
930.08 7.29 908.67 4.23
952.35 2.34 925.81 11.77
C=C syn 1757.4 3.94 1758.05 4.34
C=C anti 1737.0 4.19 ------n/a------
C-C anti ------n/a------ 1070.6 1.17
These results can be rationalized with the help of the considerations made above on the calculated frontier orbitals. The main vibration of the C-Cl bond is weaker for the diene than for the hydrogenated diene due to the HOMO-1 LUMO+2 interaction described above. In fact since the C-Cl σ* molecular orbital is unoccupied in the hydrogenated diene, the C-Cl bond is stronger. However the syn C=C double bond is almost unaffected by the hydrogenation of the other olefin as the two peaks lie within 0.7 cm-1 of each other. The weaker vibrational fequencies listed for C-Cl, although in the same region, have different energy because the major contribution to these vibrations comes from the rocking of the hydrogens of the rings. Calculated IR spectra for the two molecules can be found below.
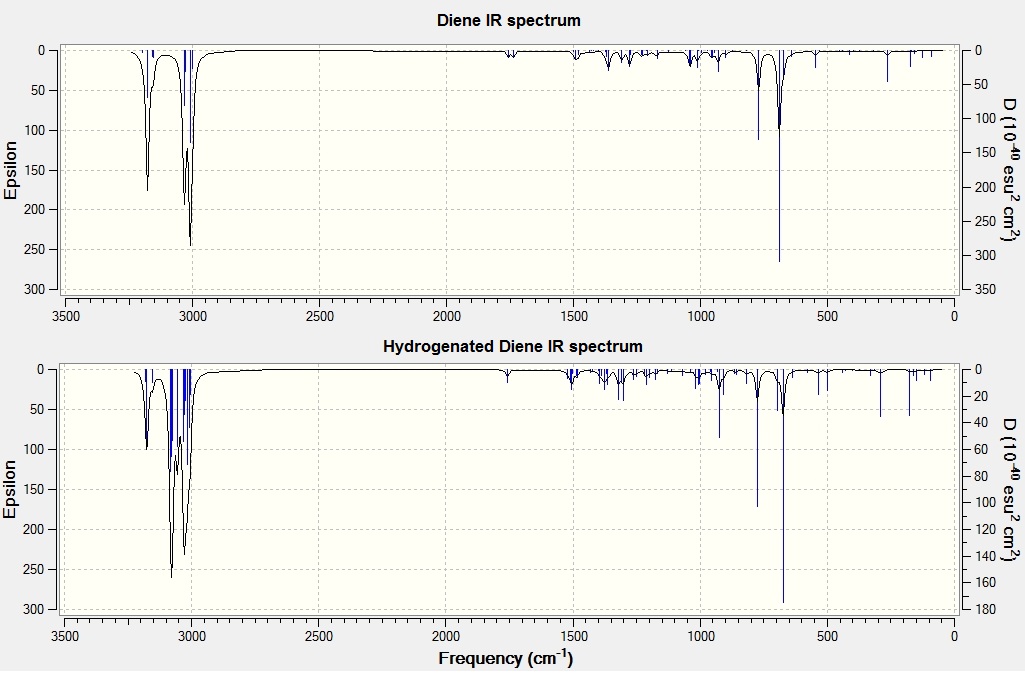
- ↑ 1.0 1.1 Brian Halton, Roland Boese and Henry S. Rzepa J. Chem. Soc., Perkin Trans. 2, 1992, 447-448 DOI:10.1039/P29920000447
Monosacharide chemistry: Glycosidation
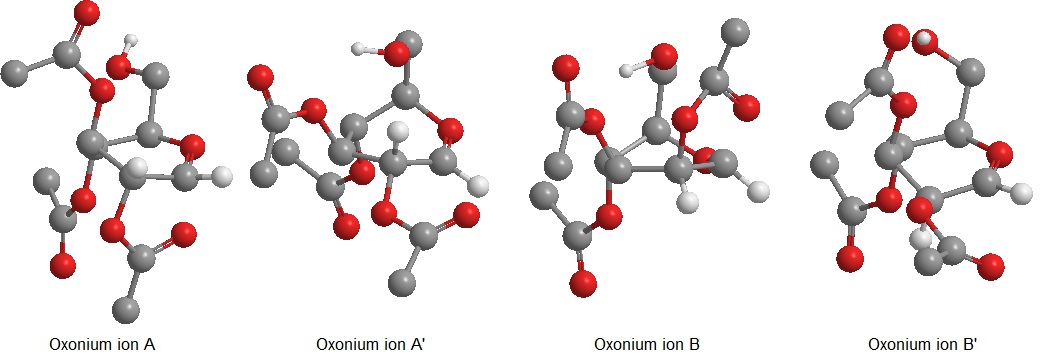
Glycosidation reactions involve the functionalization of a glycosyle donor(normally a sugar) with a glycosyl acceptor. The glycosyl acceptor can be any nucleophile. Glycosidation can be used to couple two or more sugars, in which case the product is said to be an oligosaccharide. The product of glycosidation normally leads to the creation of an α and a β anomer. The two isomers depend on the orientation of the glycosyl acceptor at the anomeric carbon. In hemiacetals the anomeric carbon corresponds to the carbon C-1 which is vicinal to the hemiacetal oxygen(the one which is part of the ring). If no precautions for selective glycosidation are taken a mixture of the to anomers is obtained. Thanks to the pioneering work of Winstein[1] anomers can be produced diasterospecifically by neighbouring group partecipation. Neighbouring group partecipation is here investigated by molecular mechanics MM2 and by PM6 semi empirical method. Methyl groups would have been sufficient to represent the R group in order to obtain a computationally and chemically valid answer, however Ac groups were used to substitute the secondary alcohols as during a synthetic route all the secondary alcohol would be substituted at once. This choice did not cause particularly longer times of computation since MM2 and PM6 methods were adopted. Glycosidation reactions go through the formation of an oxonium ion intermediate. Two couples of intermediates are possible: the A/A' couple has the C-2 acetyl group lying under the plane of the oxonium ion ring while the B/B' couple has the C-2 acetyl lying above the plane of the oxonium ion ring. The two couples of intermediates give different anomers due to neighbouring group effect. Neighbouring group effect is due to the the Ac oxygen that donates an electrons lone pair into the empty σ*-orbital of the C=O+ oxonium ion bond. Due to the quantummechanical nature of this effect we expect the MM2 force field method not to be able to detect this interaction. The energies and structures of the two couples of oxonium ions were calculated by MM2 and PM6 and found to be:
- MM2
Oxonium ion A Oxonium ion A' Oxonium ion B Oxonium ion B'
Stretch: 2.6982 2.2809 2.8404 2.6859
Bend: 17.2785 16.5131 17.3175 14.2042
Stretch-Bend: 1.3122 1.0804 1.2966 1.1736
Torsion: -7.5904 -10.1241 -5.3272 -4.1769
Non-1,4 VDW: -1.7929 -3.6537 -4.1535 -4.4592
1,4 VDW: 15.5865 16.4088 17.1698 16.0917
Charge/Dipole: -2.5693 -2.0993 -11.5147 2.5507
Dipole/Dipole: 11.9404 12.0485 12.3138 8.0525
Total Energy: 36.8631 32.4547 29.9426 36.1225 kcal/mol
- PM6
Heat of Formation = -180.9492 -164.9085 -176.466 -162.6422 Kcal/Mol
As pointed out above PM6 is a much more accurate method for this type of molecule as the semi-empirical DFT method takes into account secondary orbital interactions. The optimized structures obtained by PM6 calculations are shown above. The large difference in energy between the A/B and the A'/B' isomers due to the secondary orbital interaction can only be detected by PM6 method, in fact the MM2 calculation yields opposite (and erroneous this case) results due the the low level of theory adopted. When the oxonium ion is in its A or B conformation the interaction between the carbonyl and the oxonium antibonding orbitals stabilizes the molecule bringing the carbonyl oxygen very close to the oxonium C=O+ carbon, effectively resulting in a bond between the Ac oxygen and the C-1 carbon. Although the bond is not shown, the semi empirical quantum mechanical approach does not discriminate between formal bonds and secondary interactions. In order to prove this point MOs for both A and B isomers were calculated by PM6 method and as it can be noted in the image below there is effectively electron density between the acetyl oxygen and the C-1 carbon.
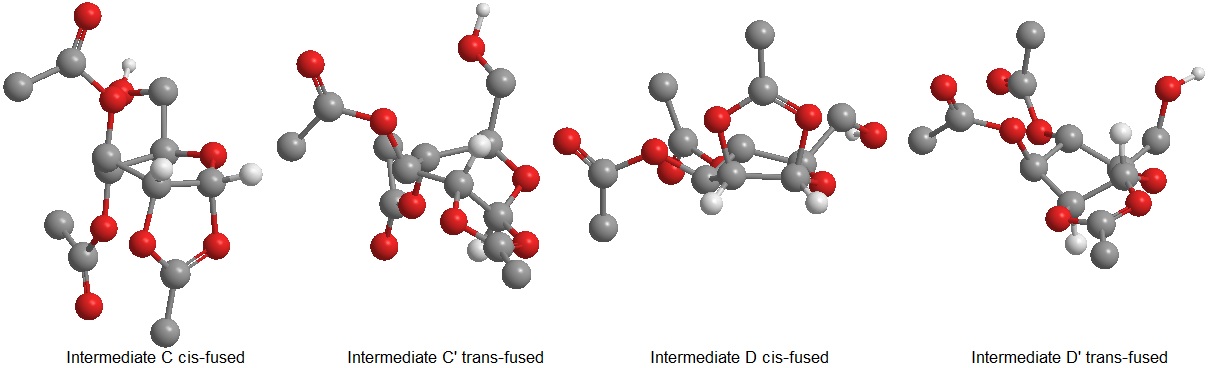Formation of a formal bond between the Ac oxygen and the C-1 oxygen leads from the A/A' and B/B' couples to C/C' and D/D' respectively. Evaluation of the energy for these intermediates calculated by both MM2 and PM6 methods is shown below . As pointed out above, the PM6 calculations for C and D produce roughly the same values obtained for A and B; the extra stabilization for C and D is due to a largely reduced torsion in the molecule as it can be assessed by inspection of the MM2 calculations. The increased torsion of the ring in A and B is most likely caused by distortion of the ring due to the oxonium C=O+ double bond.
The glycosidation reaction will be fully stereospecific only if the cis-fused ring C or D are formed, in fact the less stable trans-fused rings C' and D' will be less efficient at hindering substitution from one of the two sides of the ring. The C/C' and D/D' ratios can be calculated by Maxwell-Boltzmann statistics C/C'=e(-ΔE(j/mol)/(k*Na*T))≈10^22, therefore the amount of C'and D' compared to that of C and D is infinitesimally small. This explains the nearly 100% selectivity of the glycosidation reaction.
- MM2
Int. C cis-fused ring Int. C' trans-fused ring Int. D cis-fused ring Int. D' trans-fused ring
Stretch: 2.1752 2.8405 1.9880 2.8293
Bend: 21.3131 24.1379 22.3749 24.4264
Stretch-Bend: 1.0059 1.1488 1.0414 1.0536
Torsion: -1.1243 -0.7691 -2.2186 -2.6499
Non-1,4 VDW: -3.8840 -3.4571 -2.2859 -3.0154
1,4 VDW: 14.5749 16.4973 14.5985 16.6750
Charge/Dipole: 1.0846 4.3630 -10.5247 0.4621
Dipole/Dipole: 3.4496 5.6203 4.9648 5.5638
Total Energy: 38.5951 50.3816 29.9384 45.3450 kcal/mol
- PM6
Heat of Formation = -180.94978 -151.11416 -167.25477 -152.99433 Kcal/Mol
- ↑ S. Winstein, R. E. Buckles,J. Am. Chem. Soc., 1942, 64 (12), pp 2780–2786 DOI:10.1021/ja01264a020
Mini Project
1,8-Diarylnaphthalenes are extremely interesting molecules with an unusual geometry for organic molecules. The molecule consists of a naphthalene ring substituted at both peri positions with aryl substituents. The strong repulsion between the aryl groups causes the substituents to align each other almost perpendicular to the plane of the naphthalene and this causes π-stacking. The deformation due to the aryl rings core repulsion also causes deformation of the naphthalene ring. 1,8-Diarylnaphthalene are finding numerous applications as photoluminescent or chiral sensors and stereodynamic switchens[1]. As well as useful optically active molecules they are finding applications in organometallic chemistry for the synthesis of sandwich complexes. The steric and electronic interactions between the substituted aryl rings are important for tuning the aforementioned properties. In a recent work by Pieters,Gaucher et al. [2] library of 1,8-Diarylnaphthalenes has been sensitised by Stille-type cross coupling reactions. Here we investigate 1,8-bis(2-methoxyphenyl)naphthalene to test the experimental results reported in the work of Pieters et al.[2] . This latter system is also currently being investigated by Judge and Fuchter at Imperial College London and the results here obtained will be compared to their unpublished results attempting to resolve the discrepancies between theirs and Pieters' work.
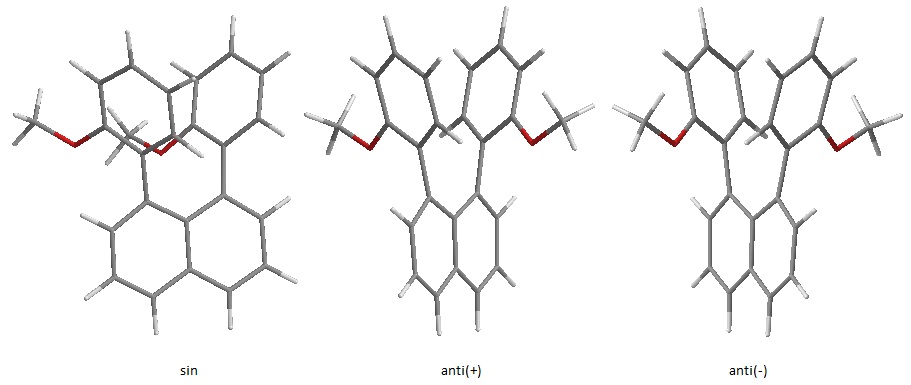
Experimental evidence reports the existence of two possible isomers for 1,8-bis(2-methoxyphenyl)naphthalene: the syn and the anti. The anti isomers exists as two enantiomers, here labeled (+) and (-), due to the difficult rotation of the substituted aryls around the naphthalene-rings. Density functional theory B3LYP/6-31G(d,p) Gaussian geometry optimization calculations were used to probe the possible conformations of the diarylnaphthalene isomers. Calculation of the energies allows us to find a difference in energy between the isomers and hence applying Maxwell-Boltzmann statistics it is possible to evaluate the ratio of anti:syn. It can be asserted with some confidence that the energies calculated are very close to the minimum energy as optimizations were conducted starting from numerous rotational transition states and they all produced the anti isomer as a result, a few examples of these will be shown later. This is in line with the crystal structures reported by Pieters and provided by Judge. The results so obtained are then compared to Pieters' and Judge's results. The experimental ratios were obtained by taking the ratio of the integrations of two NMR peaks assigned respectively to one or the other isomer. The energy calculated for the anti was -1077.06094857 a.u. while the one for the syn was -1077.05806344 a.u. The calculated difference in energy between the two is then found to be ΔEcalc=-2.885*10-3a.u = -7.5746Kj/mol. When the calculation is performed including solvation effects, the energy difference is found to be 7.2kJ/mol in Chloroform. The ratio between the anti and the syn is found by simple application of MB's statistics:Nanti/Nsyn=exp(-ΔEcalc/k*NA*T) where k is the Boltzmann's constant in J/K, NA is Avogadro's number and T is the temperature in . The calculated ratios, compared to the experimental results at 298.15K follow:
DFT Pieters Judge Nanti:Nsyn 21:1(18:1 sol) 9:1 9.6:1
From the results of Pieters and Judge, which are in good agreement, it can be found that the experimental difference in energy ΔEexpt≈5.5kJ/mol. The difference between the calculated and experimental results could be due to underestimated solvation effects and inter molecular interactions.
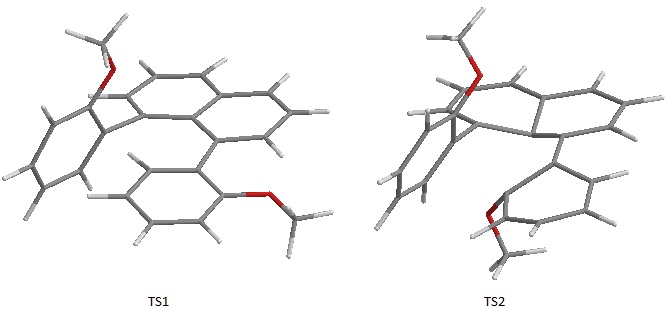
Earlier it was briefly suggested that the calculation of the energy for a few rotational Transition States were attempted. On the right the structures of two calculated transition states, TS1 and TS2 are shown. The energy difference between the ground state (anti) and the two TS (activation energies) are: ΔETS1=291.94 kJ/mol while ΔETS2=841.2 kJ/mol. Clearly the calculated energy barrier to rotation are enormous. Normally a reaction would go through the lowest energy TS, therefore TS2 can be disregarded as a possibility. TS1 is a better candidate although not enough possible conformations have been scanned to find the TS lowest in energy. It must also be considered the fact that solvation effects were not included in the calculation and these could have significantly lowered the TS energy. However the large numbers obtained give a qualitative idea of how difficult rotation is around the naphthalene axis and explains why two enantiomers of the anti-isomer exist.
The main discrepancy between Judge's and Pieters' work is in the interpretation of the C-NMR and of the syn-H-NMR. However there is good agreement between the anti-H-NMR of the two. Here an attempt to solve the discrepancy is made. It can be anticipated that overall the calculated results are in favor of Judge's interpretation.
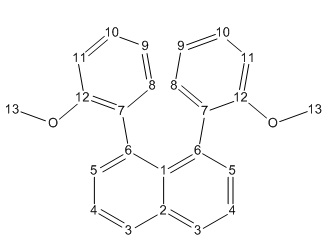
C and H NMR for both the syn and the anti isomers were calculated in chloroform. The raw data for the calculation are shown in the scheme below. In the analyzed data table the raw data peaks are grouped accordingly to the labeling shown in the scheme on the right. Although the molecule is distorted we assume that the molecule has some degree of symmetry and an average value for the shift of the grouped shifts is taken. The values so obtained are corrected by the mean difference with the experimental results as the calculated NMR have a systematic shift either below or above the experimentally determined shifts, probably due to heavy atom effect (Oxygen) and ring currents.
NMR Raw data
Position anti-δ syn-δ Position anti-δ syn-δ
10-C 44.86 55.5839 27-H 24.7773 24.2989
11-C 55.6696 53.9007 28-H 24.528 24.0289
12-C 66.4544 63.5355 29-H 24.1985 23.6813
13-C 66.0254 64.6333 30-H 24.2567 23.757
14-C 74.3201 74.8795 31-H 24.8686 24.0249
15-C 66.2927 69.0638 32-H 24.8243 24.1263
16-C 78.0662 80.2187 33-H 24.3979 24.4016
17-C 41.3659 40.5055 34-H 24.5814 24.6552
18-C 40.2873 40.8485 35-H 24.3233 24.6187
19-C 90.7485 86.0345 36-H 24.9645 25.3138
1-C 64.6323 64.2753 37-H 26.1261 24.9737
20-C 66.1382 69.4627 38-H 24.7198 24.6745
21-C 89.1813 78.434 39-H 25.1712 25.1515
22-C 38.862 62.0624 40-H 21.039 25.0459
25-C 2.7888 38.9986 41-H 28.1118 27.7056
26-C 1.8425 36.3303 42-H 12.6186 28.1193
2-C 72.9733 71.3228 43-H 27.9652 27.9097
3-C 64.5385 66.3209 44-H 28.0887 29.379
4-C 74.6814 60.8305 45-H 20.2443 29.5553
5-C 43.1308 64.7255 46-H 18.6898 29.0263
6-C 56.2771 53.9023
7-C 66.6455 68.1109
8-C 77.0767 71.6082
9-C 67.7971 64.5463
NMR analyzed data
Pos. anti_C Corrected Judge st.dev. Pos. syn_C Corrected Judge st.dev.
11 84.40735 149.80735 155.6 4.09 11 83.1266 144.7866 155.6 7.64
9 81.7507 147.1507 137.6 6.75 9 76.65675 138.31675 137.6 0.50
4 75.025 140.425 134.3 4.33 4 71.4655 133.1255 134.3 0.83
2 74.6814 140.0814 132 5.71 10 69.26325 130.92325 132 0.76
10 66.21545 131.61545 131 0.43 3 67.2159 128.8759 131 1.50
5 66.2147 131.6147 130.1 1.07 1 64.7255 126.3855 130.1 2.62
3 65.592 130.992 129.9 0.77 5 64.4108 126.0708 129.9 2.70
7 61.062 126.462 128.8 1.65 8 63.34785 125.00785 128.8 2.68
8 52.4437 117.8437 128.3 7.39 2 60.8305 122.4905 128.3 4.10
6 50.56855 115.96855 125 6.38 7 58.7181 120.3781 125 3.26
1 43.1308 108.5308 118.5 7.04 6 54.7431 116.4031 118.5 1.48
12 40.8266 106.2266 108.5 1.60 12 40.677 102.337 108.5 4.35
13 2.31565 67.71565 54.8 9.13 13 37.66445 99.32445 54.8 31.48
Pos. anti_H Corrected Judge Pieter st.dev. Pos. syn_H Pieter
11 25.5453 7.95 7.91 7.92 0.03 14 27.91153 7.92
9 24.8763 7.29 7.49 7.5 0.14 13 27.91153 7.5
5 24.8008 7.21 7.19 7.21 0.01 11 25.14375 7.21
4 24.6983 7.11 7.07 7.08 0.02 9 24.90335 7.08
10 24.5215 6.93 6.9 6.95 0.02 8 24.72375 6.95
3 24.2276 6.64 6.72 6.73 0.05 10 24.64660 6.73
8 22.7184 5.13 6.22 6.23 0.77 5 24.21260 6.23
14,13 22.3409 4.75 3.5 3.47 0.88 4 24.02690 3.79
3 23.71915 3.56
3.47
Pieters' results for C-NMR are not included above as the number of peaks reported in his paper largely outnumber the number of NMR peaks found by Judge and the number of peaks here calculated once grouped. They are reported here for completeness: Pieters' C-NMR δ = 155.5, 137.5, 134.1, 132.4, 131.9, 131.4, 130.9, 130.7, 130.1, 129.9, 128.8, 128.7, 128.2, 127.5, 124.9, 124.6, 119.0, 118.5, 108.9, 108.3, 54.7, 54.1 ppm.
As it can be asserted by inspection of the data listed above the analyzed calculated data match very well the anti-H NMR of both Pieters and Judge and the C-NMR by Judge. The C-NMR by Pieters reports 22 peaks which are probably a mixture of syn and anti. The syn-H-NMR by the latter author also outnumber the calculated data by one shift making a comparison of the two data sets not possible. Judge could not provide any NMR data for the syn-structure, in fact interpretation of the NMR spectra for the syn-isomer is very difficult due to the ratio of the two molecules and, as the calculation shows, either Pieters' interpretation is incorrect or the peaks must be assigned differently and the grouping of the calculated data must be changed.
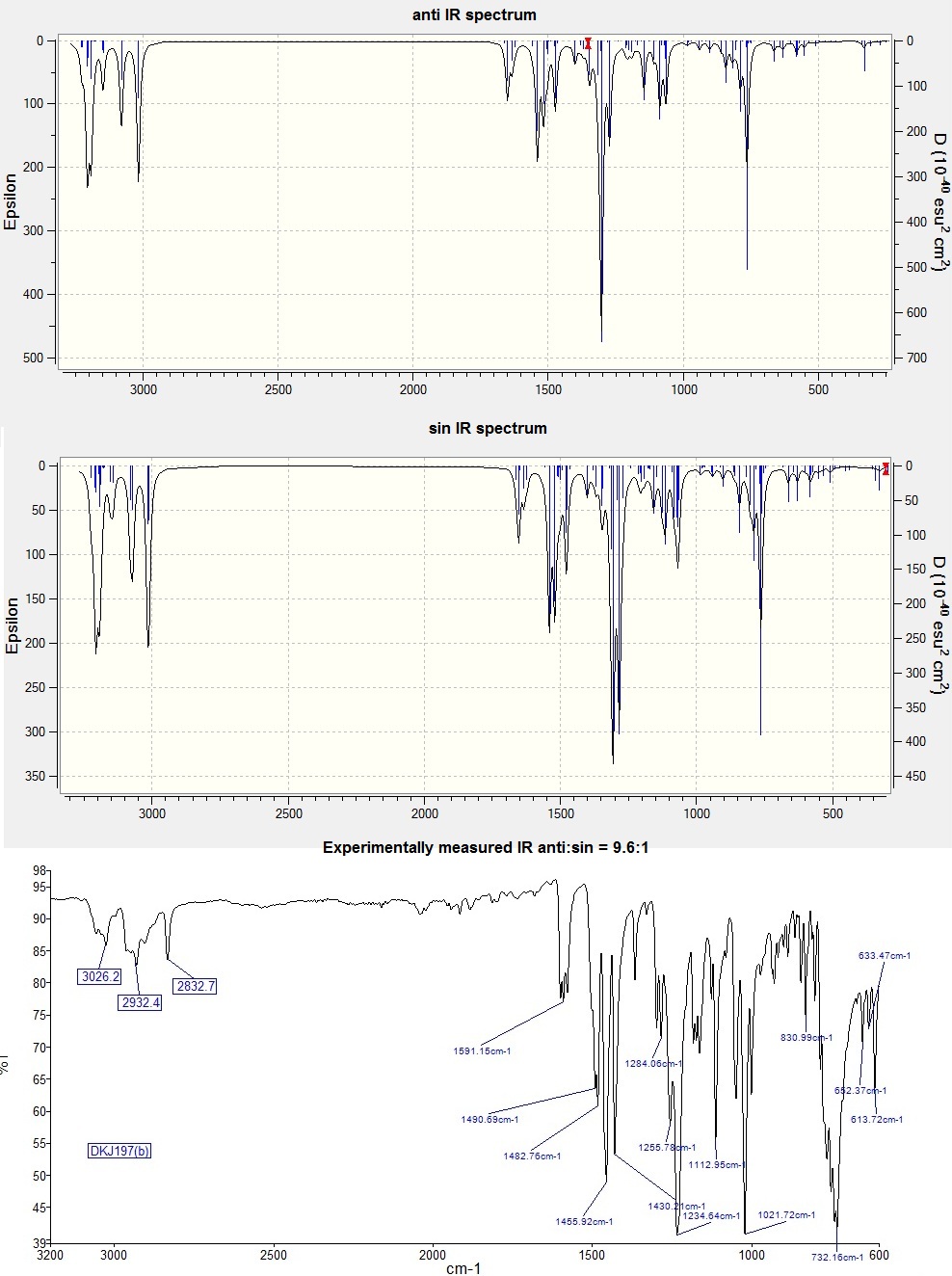
Calculation of the molecular vibrations for the two isomers were attempted and the resulting spectra are shown below along with the experimentally measured IR of a 9.6:1 mixture (anti:syn) provided by Judge.The calculated results are in good agreement with the experimental spectrum outside the fingerprint region (<700cm-1)
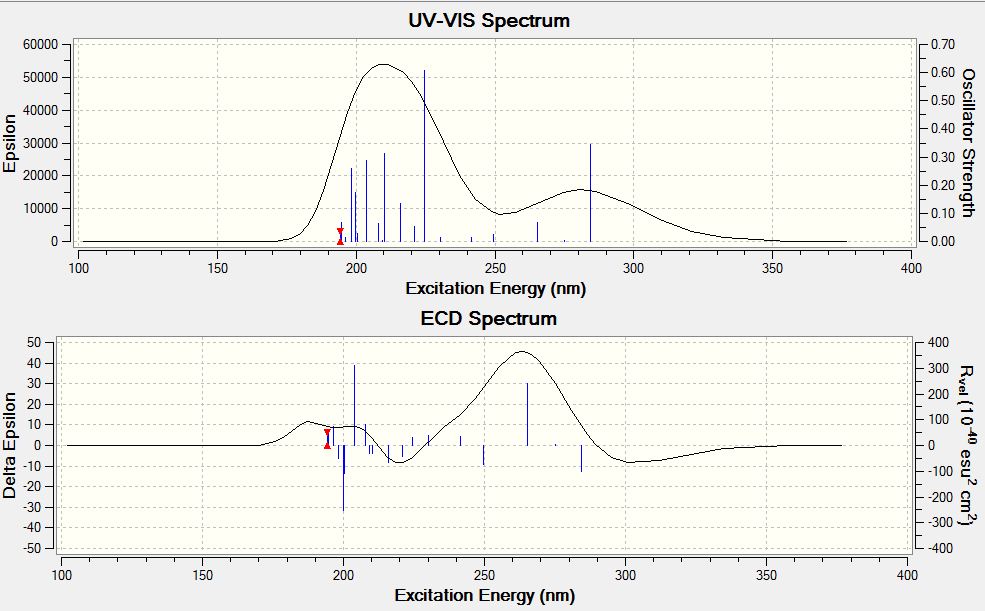
Finally the circular dichroism spectrum for the anti isomer was calcualated, in fact as mentioned earlier the isomer can exist in two possible enantiomers due to a very large rotational barrier. If the two enantiomers could be separated CD as well as optical rotation measurements would be a good way to probe the two enantiomers.
- ↑ C. Wolf, X. Mei, J. Am. Chem. Soc. 2003, 125, 10651–10658,DOI:10.1021/ja0358145
- ↑ 2.0 2.1 Grégory Pieters,Vincent Terrasson,Anne Gaucher,Damien Prim,Jerôme Marrot,2010,Eur.J.O.C.,5800–5806, DOI:10.1002/ejoc.201000685
Aknowledgements
The author would like to thank Miss D.Judge and Dr.M.Fucther for providing the results used above.