Rep:Mod:Sabrina

Name: Sabrina Maas CID: 00595314 Module: 1

Modelling using Molecular Mechanics

Recently, the importance and effectiveness of computational chemistry has largely increased. The potential uses of computational chemistry are extremely useful- with the ongoing advances in computing power, these methods will allow accurate predictions of optimised complex molecules which can then confirm and help to explain experimental results. Similarly, computational methods are increasingly used by synthetic chemists to model transition states and predict spectra. This module will investigate several different computational models and analyse the extent to which these predictions are reliable when compared to literature.

Drawing a molecule in ChemBio3D and then using the Allinger MM2 molecules mechanics model to minimise the energy produces a total energy (in kcal mol^-1) as well as optimised values for bond lengths, angles etc. This total energy can only be used to compare two different isomers, as independently it has no real measurable value. If the predominant product is known experimentally, a comparison of the calculated energies for the isomers can then be used to determine whether the reaction produces a thermodynamic or kinetic product.

The Hydrogenation of Cyclopentadiene Dimer

Cyclopentadiene is an important part of organometallic chemistry as it displays variable hapticity as a ligand, and therefore can adapt to the electronic needs of the metal centre. However, cyclopentadiene readily dimerises, decreasing the yields of the complexes containing it. This dimerisation process is facile as cyclopentadiene is able to act both as an electrophile and a nucleophile; one is the electron rich diene, and the other is the dienophile. Two cyclopentadiene molecules dimerise via a Diels-alder π4s + π2s cycloaddition with two possible outcomes, the exo (1) and endo (2) products, shown below.

Figure 1:Dimerisation giving two products: Exo Dimer 1, Endo Dimer 2

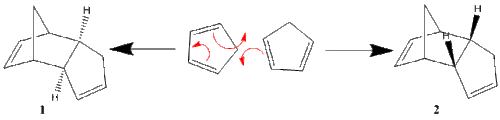
When cyclopentadiene dimerises, the dominant product is known to be the endo dimer, 2, rather than the exo dimer 1.

Using ChemBio3D and the MM2 procedures, the energies and other interactions for both dimers were calculated after optimising using MM2. These are shown below in table 1.

Table 1 - A comparison of various interactions and total energies of the exo and endo dimers minimised using MM2

Component	Energy of Exo dimer/ (kcalmol-1)	Energy of Endo dimer / (kcalmol-1)
Stretch	1.2855	1.2507
Bend	20.794	20.8476
Stretch-Bend	-0.8381	-0.8358
Torsion	7.6571	9.5109
Non-1,4 Van der Waals	-1.4171	-1.5430
1,4 Van der Waals	4.2322	4.3195
Dipole/Dipole	0.3776	0.4476
Total Energy	31.8766	33.9975

From these calculations it can be seen that dimer 1 has a total energy of 31.8766 kcalmol^-1, whereas dimer 2 has a higher energy of 33.9975 kcalmol^-1. This suggests dimer 2, which is known to be dominant, is the kinetic and not the thermodynamic product, and therefore suggests the reaction is under kinetic control. The energy component which accounts for the largest difference between dimers 1 and 2 is the torsion component. As the endo dimer has a higher torsion component, this suggests it is more strained and experiences more steric hindrance. This strain is due to two repulsions; the repulsion between the bridge-head carbon and the hydrogen atoms pointing in the same direction, and the repulsion between the carbon atoms in one double bond with those in the other.

Upon hydrogenation of dimer 2, two different scenarios could occur. Either of the two double bonds in dimer 2 can potentially be hydrogenated, resulting in two different products shown in figure 2 below.

Figure 2: Hydrogenation products: Regioisomers 3 and 4

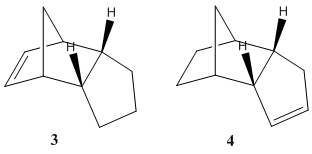
Using ChemBio3D and the MM2 procedures, the energies and other interactions for both regioisomers were calculated. These are shown below in table 2.

Table 2 - A comparison of various interactions and total energies of the dihydro derivative regioisomers minimised using MM2

Component	Energy of Product 3/ (kcalmol-1)	Energy of Product 4 / (kcalmol-1)
Stretch	1.2771	1.0968
Bend	19.8664	14.5241
Stretch-Bend	-0.8346	-0.5491
Torsion	10.8068	12.4979
Non-1,4 Van der Waals	-1.2257	-1.0701
1,4 Van der Waals	5.6330	4.5119
Dipole/Dipole	0.1621	0.1406
Total Energy	35.6850	31.1520

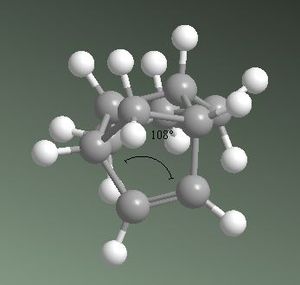
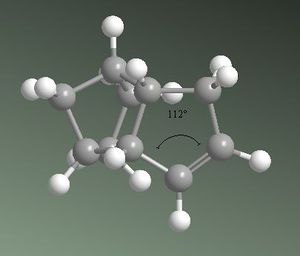
From these calculations it can be seen that product 3 has a total energy of 35.6850 kcalmol^-1, whereas product 4 has a lower energy of 31.1520 kcalmol^-1. This suggests product 4 is the thermodynamically favoured product, and therefore it is easier to hydrogenate the double bond located in the 6-membered ring. This may be explained by analysing the energies related to angular strain associated with both products. The ideal sp² carbon angle is 120^o. In product 3, the sp² carbon angle is 107.8^o and in product 4 it is 112.4^o. Both products show angles that are more compressed than ideality, leading to an increase in the bend energies. Product 3 exhibits a higher bend energy as it is more strained, supporting that product 4 is preferred thermodynamically. This is shown in figures 2a and 2b below. Product 3 also has higher energy components due to stretching and van der Waals, however has a lower torsion energy component than product 4. This torsion component is not large enough to counteract the other higher energy components, therefore product 4 is still overall more thermodynamically stable. This does not, however, determine whether the reaction will proceed under thermodynamic or kinetic control, nor does it determine which is the kinetic product.

Figure 2a: Hydrogenation product 3 angle strain

Figure 2b: Hydrogenation product '4 angle strain

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

The organic compound taxol is an important drug in the treatment of ovarian cancers. In the synthesis proposed by Paquette, a key intermediate is synthesised with the carbonyl group pointing up (5) or down (6) as shown in figure 3 below. These two intermediates are atropisomers as they differ because of restricted rotation around a carbon-carbon single bond due to steric hindrance with the bridgehead group. Atropisomers can be equilibrated thermally, which is a result observed in the proposed synthesis; it was found that on standing, the initally produced compound isomerises to the other carbonyl isomer.

Figure 3:Carbonyl isomers 5 and 6

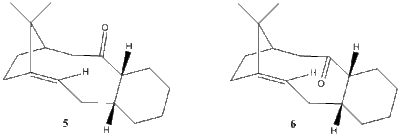
By determining the relative energies of these atropisomers, it can be determined which isomer is the kinetic intermediate and therefore formed first, and which is thermodynamically more stable. Both MM2 and MMFF94 force-field molecular mechanics models are used to calculate the total energies shown in table 3 below. Two different conformations of the 6-membered ring for each isomer are possible: chair conformation or the higher-energy twist-boat conformation. It is assumed that the twist-boat has an energy that is too high for the compound to exist, and therefore the only intermediates identified below are chair conformations.

Table 3 - A comparison of the energies of the taxol intermediates isomers minimised using MM2 and MMFF94

Component	Energy of Atropisomer 5/ (kcalmol-1)	Energy of Atropisomer 6 / (kcalmol-1)
Stretch	2.7833	2.6222
Bend	16.5389	11.3389
Stretch-Bend	0.4303	0.3438
Torsion	18.2525	19.6666
Non-1,4 Van der Waals	-1.5504	-2.1574
1,4 Van der Waals	13.1100	12.8709
Dipole/Dipole	-1.7250	-2.0021
Total Energy (MM2)	47.8396	42.6830
Total Energy (MMFF94)	70.5501	60.5627

This table clearly shows that isomer 5 is the kinetic product (higher total energy) which is initially formed and isomer 6 is the thermodynamic product which is slowly formed upon standing. The MM2 and MMFF94 force-field models produce similar results, with both predicting isomer 6 to have the lowest total energy, with MMFF92 predicting a 9.9874 kcalmol^-1 energy difference and MM2 a slightly smaller energy difference of 5.1566 kcalmol^-1. From the table above, it can be seen that the largest energy difference between isomers 5 and 6 is due to the bending component. This is due to the angle of the sp² carbon, which is further from the ideal 120° in isomer 5 (126.6°) than in isomer 6.(123.6°) The MM2 and MMFF94 methods agree in this scenario as the molecules are simple enough to handle for the MM2 model. If formal charges were present on the atoms, it would be noticeable that MMFF94 is more accurate in predicting the energies as it can take into account electrostatic interactions. MM2, on the other hand, can only treat two bonded atoms as a classical two-body spring potential.

Hyperstable Alkenes

A hyperstable alkene is an alkene that shows a negative olefinic strain energy. Olefinic strain energies may be calculated as follows:

Olefinic Strain Energy = Total Energy of Olefin - Total Energy of Hydrogenated Derivative

The hydrogenation of an alkene with a negative olefinic strain energy is known to be extremely slow. By calculating the energy of the hydrogenated taxol intermediate, the unreactivity of the alkene will be explained.

Table 4 - A comparison of the energies of intermediate 6 and its hydrogenated intermediate 6 minimised using MM2 and MMFF94

Component	Energy of Intermediate 6/ (kcalmol-1)	Energy of Hydrogenated Intermediate 6 / (kcalmol-1)	Energy Difference (olefin - hydrogenated)/ (kcalmol-1)
Stretch	2.6222	3.0967	-0.4745
Bend	11.3389	14.3879	-3.049
Stretch-Bend	0.3438	0.5792	-0.2354
Torsion	19.6666	19.4672	0.1994
Non-1,4 Van der Waals	-2.1574	-0.9995	-1.1579
1,4 Van der Waals	12.8709	15.4953	-2.6244
Dipole/Dipole	-2.0021	-1.7292	-0.2729
Total Energy (MM2)	42.6830	50.2977	-7.6147
Total Energy (MMFF94)	60.5627	75.7743	-15.2116

Both the MM2 and MMFF94 calculations for the total energy of isomer 6 and its hydrogenated product show that the formation of this hydrogenated product is unfavourable, as a higher energy is observed. The difference, which corresponds to the olefinic strain energy, is shown in the above table to be -7.6147kcalmol^-1. The largest contributions to this olefinic strain energy are the bend energy, non-1,4 van der Waals and 1,4-van der Waals energy components. Upon hydrogenation, the two carbon atoms which had a double bond between them change from a hybridisation of sp² to sp³. This has an effect on the bond angle surrounding those carbon atoms, which changes from 124.2° in isomer 6 and 118.9° in the hydrogenated product. In the hydrogenated product, the angle is therefore very far away from the ideal sp³ angle of 109.5°, whereas the angle in isomer 6 is not far from the ideal 120°. Therefore more strain is experienced in the hydrogenated product, increasing the energy.

The van der Waals energy differences are due to the number of repulsive interactions between hydrogen atoms in the molecule. It is known that interactions between hydrogen atoms at distances less than or equal to 2.1 Å are repulsive. In figures 4 and 5 below, it can be seen that two repulsive interactions are found in the hydrogenated product, but merely one is found in the alkene isomer 6.

Figure 4:Repulsive van der Waals interactions alkene bridgehead

Figure 5:Repulsive van der Waals interactions hydrogenated product

Modelling using Semi-empirical Molecular Orbital Theory

Regioselective Addition of Dichlorocarbene

Using semiempirical calculations such as MOPAC, which provide representations of valence-electron molecular wavefunctions and therefore a more quantum mechanical treatment of the molecule, this section will show why compound 7, otherwise known as 9-chloromethanonaphthalene, shows π-selectivity when reacting with electrophiles. The [1+2] cycloaddition of compound 7 with dichlorocarbene is shown in figure 6 below.

Figure 6: Addition of dichlorocarbene to compound 7

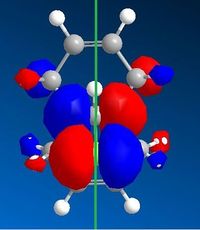
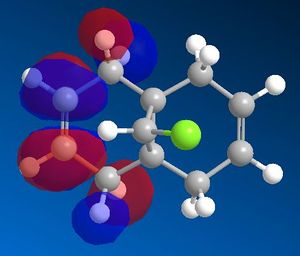
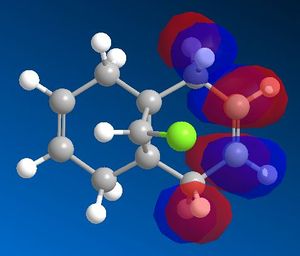
After optimising the structure of 7 using MM2, the structure was then run using the MOPAC interface with PM6 as the method. This, however, gave unexpected results. Compound 7 is known to have a point group C_s which contains a σ_h symmetry plane. This strongly suggests the molecular orbitals should also be symmetrical across this plane, which cuts through the chlorine atom and the carbon double bonds. Using the method PM6, the molecular orbitals produced did not show this expected symmetry. An example of the HOMO, which is thought to be the most reactive towards electrophiles, generated using PM6 can be seen in figure 7 below. The green line represents the symmetry plane, showing clearly that the orbitals are not symmetrical across the plane.

Figure 7: HOMO generated using PM6

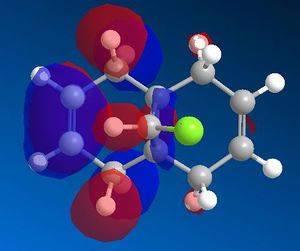
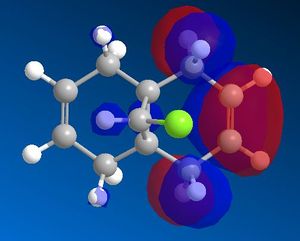
The MOPAC interface using AM1 as the method produced the expected symmetrical molecular orbitals. These are shown in table 5 below.

Table 5 - Molecular Orbitals for Compound 7

HOMO -1	HOMO	LUMO	LUMO + 1	LUMO + 2

From the molecular orbital representations above, it can be seen that a large proportion of the electron density in the HOMO is located on the syn alkene. This is the alkene that is syn to the chlorine atom, or in other words on the same side of the molecule as the chlorine atom. As mentioned above, the HOMO is thought to be the most important for the reaction with electrophiles. This is because it is the orbital in which the highest energy electrons are located, making it the most nucleophilic and therefore the most reactive towards electrophiles. The reaction of compound 7 with dichlorocarbene is similar to an electrophilic addition, therefore it is the syn alkene that is best able to donate electron density into the lowest unoccupied molecular orbital of the dichlorocarbene in the case of an electrophilic attack. On the other hand, it can be seen that the LUMO has a large proportion of the electron density positioned at the anti alkene. This suggests the anti alkene can experience nucleophilic attack from an electron donating species.

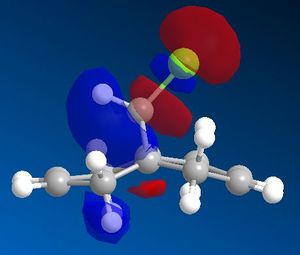
The LUMO+2 molecular orbital seems to depict the σ^*(C-Cl) anti-bonding orbital, which is a very good electron acceptor due to the highly electronegative chlorine atom. This causes the carbon atom to be electron deficient, which may promote a stabilising interaction from the electrons in the π(C=C) anti alkene orbital.

From the above diagrams it can also be seen that the HOMO-1 has a large electron density build-up on the anti alkene. As this is an occupied molecular orbital, it could be thought to behave as a nucleophile and attack the electrophilic dichlorocarbene species. This interaction, however, will have a lower stabilisation energy than the overlap between the HOMO and the dichlorocarbene LUMO. This is due to the Klopman Salem equation: E_stab α s² / ΔE_i. The larger the interaction energy, the smaller the stabilisation energy. The HOMO has the highest energy electrons and therefore produces a smaller interaction energy with the dichlorocarbene LUMO than the HOMO-1. This is clearly shown in figure 8 below.

Figure 8: Different stabilisation energies for HOMO and HOMO-1

The influence of the C-Cl bond on the vibrational frequencies of the carbon- carbon double bonds in both compound 7 and its monohydrogenated derivative, where the anti alkene is hydrogenated, is analysed below. The geometry of both compounds were optimised using MM2 and then MOPAC. An input file was saved to run B3LYP/6-31G(d,p) on the Gaussian interface, and saved as a .gjf file which was then submitted to SCAN. The output file was used to generate vibrational spectra on Gaussview 5.0 for both compounds, shown in figures 9 and 10. The prediction from the molecular orbital discussion above is confirmed; the C-Cl bond length is decreased (and therefore the C-Cl vibration is found at a higher frequency) in the monohydrated product. This is due to the removal of the anti alkene, which means the π(C=C) to σ^*(C-Cl) interaction discussed above is no longer present. Any lack of electrons being donated into an anti-bonding orbital will ultimately stabilise the C-Cl bond, therefore increasing its strength and decreasing its bond length. This can be clearly seen in the vibration frequencies of the C-Cl bonds seen in table 6.

Figure 9: IR Spectrum of compound 7

Figure 10: IR Spectrum of monohydrogenated derivative of compound 7

Table 6 - Summary of Relevant Data from the Vibrational Spectra for compound 7 and Monohydrogenated derivative of compound 7

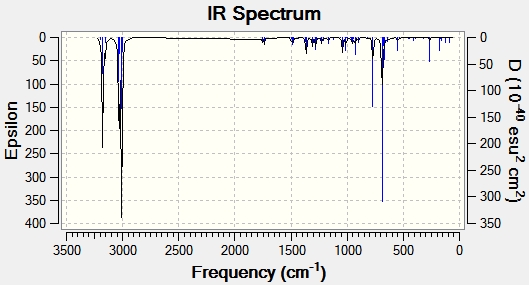
Type of Bond Vibration (cm-1)	Molecule
	Compound 7	Monohydrogenated derivative of 7
C-Cl	770.92	779.93
C=C (syn)	1757.33	1753.76
C=C (anti)	1736.99	n/a

This data confirms the reasoning given above as the C-Cl bond frequency is 9.01 cm^-1 lower, and therefore weaker than in the diene species. This therefore strongly suggests there is an interaction between the π(C=C)orbital and the σ^*(C-Cl) orbital. This can be further confirmed by analysing the effect of electron withdrawing and donating groups on the anti-alkene.

Using the same reasoning as above, the presence of an electron withdrawing group on the anti-alkene suggests less electron density will be present in the π(C=C)orbital, and therefore less electron density can be donated into the σ^*(C-Cl) orbital. This would increase the C-Cl bond strength and therefore frequency of vibration. The presence of an electron donating group on the anti alkene suggests more electron density will be available in the π(C=C)orbital , and therefore more electron density can be donated into the σ^*(C-Cl) orbital. This would weaken the C-Cl bond and it should appear at lower frequencies in the IR spectra.

To confirm this, compound 7 with different substituents on the anti-alkene were studied. The vibrational frequency results are shown below in table 7. The IR spectra can be seen by clicking on the relevant molecule titles.

Table 7 - Summary of Relevant Data from the Vibrational Spectra for compound 7 with different anti-alkene substituents

Type of Bond Vibration (cm-1)	Molecule
	Compound 7	NO2 substituent	OMe substituent
C-Cl	770.90	771.58	765.15
C=C (syn)	1757.33	1758.07	1756.34
C=C (anti)	1736.99	1738.86	1736.63

The above results clearly conform to the prediction explained above. The C-Cl bond is stronger and therefore shorter when the anti-alkene has an electron withdrawing substituent (NO₂) and weaker and therefore longer when the anti-alkene has an electron donating substituent.(OMe)

Monosaccharide chemistry: Glycosidation

During glycosidation, a leaving group is forced to leave the cyclohexane ring by the push of a lone pair of electrons from the oxygen within the ring. This forms an intermediate oxonium cation. According to the orientation of the OAc group on the adjacent carbon, two different anomers with almost complete diastereospecificity can be formed. To form the alpha anomer, the intermediate oxonium cation in D must be formed from the top face, as can be seen in structure B. This forces the nucleophile to attack from the bottom face. To form the beta anomer on the other hand, the intermediate oxonium cation in C must be formed by the attack of the oxygen from the bottom face. This forces the nucleophile to add in the anomeric position from the top face. This can be seen in figure 11 below.

Figure 11: Glycosidation mechanisms showing the formation of α- and β- anomers

To keep the computational demand minimal, an R group should be chosen that although is not as complex as, for example, R=Ac, which is often used in protecting group chemistry, still represents the steric bulk provided by the substituent. Using R=Ac would produce high computational demands as it has a large size and hydrogen bonding would have to be taken into account. If R is small, for example a hydrogen atom, sterics would not reflect reality and would also produce hydrogen bonding interactions due to the presence of hydroxyl groups. Therefore it was decided that, for the purpose of the computational methods used below, R would be represented by a methyl group.

By experimenting with the MM2 and MOPAC/PM6 methods, it was found that MOPAC/PM6 was better suited for the calculations than MM2. This is because MM2 seems to work well for simple hydrocarbons with limited substituents, and does not seem to work well with carbocations and conjugation within molecules. It did not seem to recognise the stabilising interaction between the oxonium cation and the lone pair of electrons on the acetyl oxygen. It is a purely mechanical method that is unable to form new bonds. On the other hand, the semi-empirical method MOPAC/PM6 was able to model the conjugation in the molecules and therefore could model the neighboring group effect. The electrostatic interactions were better modelled and the method is able to suggest the formation of new bonds by virtue of the distance between two atoms.

As can be seen in figure 11 above, A consists of the OAc group being in the equatorial position and below the plane of the 6-membered ring. A' therefore also consists of the OAc in the equatorial position however above the plane of the 6-membered ring. B consists of the OAc group in the axial position above the plane of the ring, and B' therefore has the OAc group below the plane of the ring but still axial. C has the 5-membered ring in the equatorial position below the plane of the 6-membered ring and C' is the same however above the plane of the 6-membered ring. D consists of the 5-membered ring in the axial position above the plane of the ring, and D' is the same however below the plane of the 6-membered ring.

Table 8 - A comparison of various interactions and total energy of A, A', B, B', C, C', D, D modelled using MM2 and the delta H of formation calculated using MOPAC/PM6

Component	Energy of A MM2 and PM6/(kcalmol-1)	Energy of A' MM2 and PM6 /(kcalmol-1)	Energy of B MM2 and PM6 /(kcalmol-1)	Energy of B' MM2 and PM6/(kcalmol-1)	Energy of C MM2 and PM6/(kcalmol-1)	Energy of C' MM2 and PM6/(kcalmol-1)	Energy of D MM2 and PM6/(kcalmol-1)	Energy of D' MM2 and PM6/(kcalmol-1)
Stretch	2.9375	3.2965	2.4380	2.4612	1.8870	2.0833	1.7148	2.0620
Bend	11.3902	13.2324	10.7764	14.5179	11.8389	12.7086	14.2840	12.8531
Stretch-Bend	1.0212	1.2354	0.9450	1.1078	0.6582	0.8004	0.5621	0.7818
Torsion	1.7370	1.0130	2.1604	1.3870	8.8866	9.7096	6.9009	9.8055
Non-1,4 Van der Waals	0.5669	-0.5792	-2.2454	-2.1688	-3.4174	-3.4059	-5.2472	-3.8369
1,4 Van der Waals	18.2530	17.2489	19.1699	17.6213	18.9472	17.5265	18.4066	19.0037
Charge/Dipole	-11.5535	-7.4772	-8.9053	4.2191	-4.3956	1.0840	-0.8136	-1.5985
Dipole/Dipole	6.7374	6.7847	5.6014	5.3703	-0.9325	0.3830	-0.4079	-0.9510
Total Energy using MM2	31.0897	34.7546	29.9403	44.5157	33.4723	40.8895	35.3998	38.1198
ΔH energy of formation using MOPAC/PM6	-82.78890	-61.89125	-90.51306	-78.58201	-91.65352	-62.07907	-91.64179	-74.51324

The results in the table above show several things. Firstly, the MM2 and MOPAC/PM6 methods are not completely contradictory. In fact, both methods showed the same relative stabilities between the original compound and its 'prime,' where the OAc or 5-membered ring is on the opposite side of the plane of the 6-membered ring. For example, A shows a lower energy and ΔH energy of formation using both MM2 and MOPAC/PM6 than A', suggesting the compound with the OAc equatorial and below the plane of the ring is more stable than the OAc group equatorial and above the plane of the ring.

Using MM2, it was found that the main energy difference between the acetyl group or oxonium ring pointing above or below the oxonium cation in the 6-membered ring is due to a difference in charge-dipole energy. This is because the MM2 method is unable to recognise the oxonium ion for what it is and merely treats it as an oxygen atom with a positive point charge. The magnitude of the charge-dipole energy is therefore dependent on the distance between the oxygen cation and the lone pair on the oxygen in the acetyl group. This suggests A' and B' have slightly longer distances between the oxygen lone pair and the oxonium cation as the charge/dipole energies are more favourable than the than their A and B counterparts.

Using MOPAC/PM6, the heat of formations were calculated. The results in table 8 above show that there are similarities between the heat of formations of A/C and B/D. This suggests that the MOPAC/PM6 method is capable of creating new bonds between two atoms. (in this case the oxygen in the acetyl group and the carbon adjacent to the oxonium ion) Although the bonds are not drawn in by the method, these are clearly apparent when measuring the C-O bond distances. The bond lengths found for A and B clearly show a formation of a bond as they are around the typical length of a C-O bond of 0.143nm, whereas in A' and B' a bonding interaction is not formed. These bond lengths are shown in table 9 below. Another factor that affects the stability of A/A' and B/B' is the Burgi-Dunitz angle. The ideal angle of attack of a nucleophile towards an sp² hybridised atom is 107^°. For A and B, the angle between the oxygen lone pair and the carbon atom adjacent to the oxonium cation is close to this ideal angle. For A' and B', the angle deviates from ideality, therefore resulting in a higher energy.

Table 9 - C-O Bond lengths and angle of attack comparisons

Compound	C-O Bond Length / Å	Angle of attack /°
A	1.574	104.4
A'	4.29	130.9
B	1.550	106.2
B'	4.99	140.6

Mini Project - Enantioselective [2+2+2] Cycloaddition of alkenyl isocyanates and terminal alkynes

[2+2+2] cycloaddition reactions catalysed by transition metals are very good methods for synthesising polycyclic carbocycles and heterocycles with structural and functional complexity. Robert T. Yu and Tomislav Rovis reported a general and efficient route to many indo- and quinolizidine alkaloid natural products, using pentyl isocyanate and different alknenyl isocyanates. The reaction used is a step in the total synthesis of (+)-Lasubine II.

For the purpose of this mini-project, the two regioisomeric products E and F of the regioselective reaction shown in figure 12 below will be analysed.

Figure 12: Formation of E and F

To form E, a simple [2+2+2] cycloaddition occurs. To form F, a CO migration must occur before the cycloaddition, in order for the ketone and phenyl group to occupy the right positions. By merely looking at the reaction scheme it is impossible to tell which regioisomer is thermally favoured. In this mini-project, computational methods will be used to find the lower energy isomer and hence explain the selectivity of the reaction. Then, spectra for both products will be predicted using computational methods which can then be compared to literature in order to evaluate the methods used.

Analysis of Energies

Literature reports the dominant product to be F, with the ratio of E:F being 1:7.3. In order to determine the most thermodynamically stable product, the molecules E and F underwent geometry optimisation using the MM2 and then MOPAC/PM6 methods. The results are summarised in table 10 below.

Table 10 - A comparison of the energies of the regioisomers E and F

Component	Energy of Isomer E MM2 / PM6 / (kcalmol-1)	Energy of Isomer F MM2 / PM6 / (kcalmol-1)
Stretch	1.5226	1.8440
Bend	8.3377	14.0557
Stretch-Bend	-0.0113	0.1981
Torsion	-4.4601	3.7864
Non-1,4 Van der Waals	1.2659	3.0548
1,4 Van der Waals	14.1286	15.3433
Dipole/Dipole	-8.4538	-0.9195
Total Energy (MM2)	12.3297	37.3627
Heat of Formation PM6	-2.71712	-10.17611

One of the things that can be realised by inspecting the jmol files within the table is that the MM2 optimised geometry is more planar than the MOPAC/PM6 optimised geometry for both isomers. The PM6 method seems better suited to deal with atoms such as nitrogen as it is non-planar in PM6, as expected, yet is planar in MM2.

The total energy calculated using MM2 produces a lower energy for isomer E by 25.033 kcalmol^-1, which is quite a large difference. MM2 therefore suggests isomer E to be the most thermodynamically stable. The largest energy difference is due to the bending component. This could be due to the strain associated with the phenyl ring being close to the 5-membered ring containing the nitrogen. However, using the MOPAC/PM6 method, the ΔH heat of formation of F is lower and therefore suggests isomer F is the most thermodynamically stable. Seeing as the nitrogen is non-planar in this computational method, as is expected for an sp³ nitrogen with a lone pair, it seems to more accurately depict reality. The MOPAC/PM6 method is therefore used to optimise the geometries of the isomers before producing spectra below.

¹³ C NMR Spectroscopy

The structures of E and F were drawn in ChemBio3D and the energies were minimised first using MM2 and then MOPAC/PM6. These geometries were then DFT optimised using SCAN. The resulting files were then edited in order to resubmit it to SCAN to calculate the NMR spectra.

Figure 13: ¹³ C NMR of isomer E

Figure 14: ¹³ C NMR of isomer F

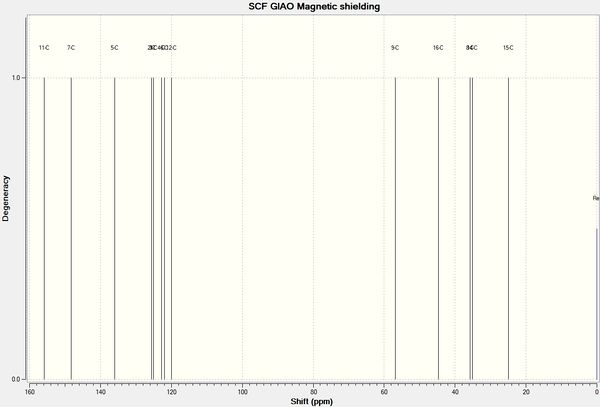
The numbering used to distinguish between carbon environments in table 11 is shown in figure 15.

Figure 15: ¹³ C NMR environment numbering

Table 11 - ¹³C NMR, Reference = TMS mPW1PW91/6-31G(d,p) CDCl₃ GIAO

Environment	E				Environment	F
	13C Peak Shift (δ,ppm)					13C Peak Shift (δ,ppm)
	Computationally Predicted	Literature value <ref="miniproj"></ref>	Difference			Computationally Predicted	Literature value<ref="miniproj"></ref>	Difference
11	155.9	164.2	-8.3		2	183.8	192.2	-8.4
7	148.2	148.7	-0.5		6	158.6	163.1	-4.5
5	136.0	138.1	-2.1		7	134.9	136.4	-1.5
2	125.6	129.5	-3.9		10	127.1	130.0	-2.9
3	125.1	129.0	-3.9		8	125.34	128.7	-3.4
1	125.0	126.1	-1.1		9	125.26	127.8	-2.5
4	122.7	121.0	-1.7		12	126.0	-	-
6	122.0	-	-		11	125.5	-	-
12	119.9	-	-		1	99.5	100.2	-0.7
9	56.9	56.8	0.1		4	58.8	59.1	-0.3
16	44.7	44.2	0.5		16	52.1	49.5	2.6
8	35.7	33.7	2.0		3	40.8	41.7	-0.9
14	35.1	33.4	1.7		14	31.5	32.2	-0.7
15	24.9	23.3	1.6		15	27.8	24.7	3.1

From the table above, it can be seen that the chemical shifts between the computational prediction and the literature values are not significantly different. The range of differences are explicitly shown in figure 16.The largest difference between literature and the prediction is around 8ppm is for the highest chemical shift peak. This could be due to the limitations of the modelling system used. If more time was available, a modelling system with more parameters may yield chemical shifts closer to literature.

The lack of peaks in literature for environments 6 and 12 in E and 11 and 12 in F is most likely due to overlapping peaks that were not distinguishable due to the carbon atoms being in aromatic rings and therefore producing similar chemical shifts.

The carbon NMR seems to be a useful method in distinguishing between isomers as the carbonyl oxygen, labelled 11 in E and 2 in F, produce chemical shifts that differ by 27.9ppm. Similarly, the carbon atom β to the carbonyl carbon, ie the one adjacent to the phenyl ring, labelled 7 in E and 6 in F, produce chemical shifts that differ by 10.4ppm.

Figure 16: ¹³ C NMR relative errors of predicted to literature chemical shifts

It is difficult to compare these graphs at first sight, as the carbon atoms are differently numbered in both compounds. However, it can be seen that there is a trend in the difference for the phenyl carbons, which are labelled 1-5 in E and 7-10 in F, and show a negative difference, and the carbons in the 5-membered ring, labelled 14-16 in both E and F, which show a positive difference.

IR Spectroscopy

The geometry of compounds E and F were optimised using MM2 and then MOPAC. An input file was saved to run B3LYP/6-31G(d,p) on the Gaussian interface, and saved as a .gjf file which was then submitted to SCAN. The output file was used to generate vibrational spectra on Gaussview for both compounds, shown in figures 17 and 18.

Figure 18: IR of isomer E

Figure 18: IR of isomer E

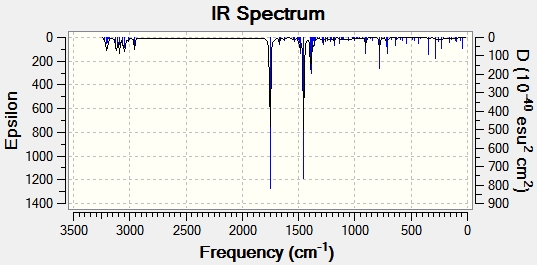
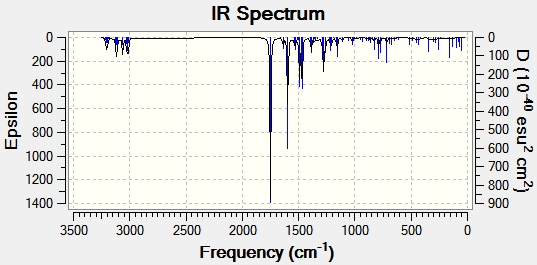
The important IR spectral data is shown in table 12 below.

Table 12 - Summary of Relevant Data from the Vibrational Spectra for isomers E and F

Type of Bond Vibration (cm-1)	Molecule
	E	Literature E values	F	Literature F values
C=O stretch	1753.25	1644	1749.91	1624
C=C aromatic stretch	1486.40	1593	1596.09	1532
C=C aromatic stretch	1454.87	1450	1491.42	1460
C=C aromatic stretch	-	-	1467.62	-
C-N stretch	1389.54	1352	1292.37	1260
C-H bend phenyl	780.90	-	790.79	-

From the above data, it can be seen that the C=O stretch is at a slightly higher frequency for E than for F, both in the predicted spectrum and the literature values. The C=C bonds are all in the same frequency region and therefore are not of much use to distinguish the molecules. The characteristic C-N bond, on the other hand, is very useful in doing so. It appears at a higher frequency for E than for F. This difference is quite apparent, being different by 97.17cm^-1 in the computed spectrum, and 92cm^-1 in literature. This suggests the C-N peak can be used to determine the presence of either isomer.

Overall, there are relatively large discrepancies between the literature values reported and the frequencies predicted by the computational method. Although they differ by a value of 110cm^-1 on average, it can be seen that the trend between the relative strengths of isomers E and F are is apparent. This relatively large error between the literature and computational values can be reduced by assuming the predicted stretching vibrations are systematically too high by 8%. Taking this into account, the difference on average between literature and the prediction is reduced to 86cm^-1.

The literature has not reported C-H phenyl asymmetric and symmetric stretches around 2900-3200cm^-1 which can clearly be seen in the predicted spectra.

The sum of electronic and thermal free energies was found to be 672.3108 Hartrees for isomer E and 672.2949 Hartrees for isomer F. This suggests isomer F has a lower free energy by 9.98 kcalmol^-1. This agrees with the energy analysis performed previously, where isomer F had a lower heat of formation energy calculated using MOPAC/PM6.

Optical Rotation and Circular Dichroism

To determine the optical rotation of isomers E and F, the optimised energy input file used for the NMR calculation was saved as a .gjf file and edited on wordpad so the first line read #cam-b3lyp/ 6-211G(d,p) polar(optrot) scrf(IEFPCM, solvent=chloroform) CPHF=RdFreq. This file was submitted to SCAN and the optical rotation was found in the log output file. The results, as well as the literature values, are reported in table 13 below.

Table 13 -Calculated optical rotation values of E and F compared with literature

Compound	Optical rotation [α]D20	Literature [α]58920
isomer E	-26.82	+166.9
isomer F	+619.65	+640.0

The optical rotation value calculated by Gaussian for isomer F is very similar to literature. For isomer E, the value has the incorrect sign. This could be due to the inaccuracy of the method for calculating optical rotations around the order of magnitude of 100 and below. Nevertheless, it seems as though optical rotation is a useful method in determining which isomer is present.

To calculate the circular dichroism spectra, the optimised energy input file used for the NMR calculation was saved as a .gjf file and edited on wordpad so the first line read #cam-b3lyp/ 6-211G(d,p) td(Nstates=20) scrf(IEFPCM, solvent=chloroform). The file was then submitted to SCAN and the circular dichroism spectra was generated in gaussview using the output file. The spectra for isomers E and F can be seen in figures 19 and 20 below.

Figure 19: CD of isomer E

Figure 20: CD of isomer F

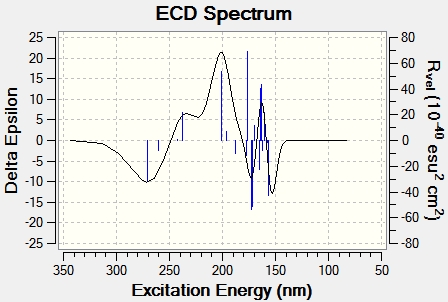
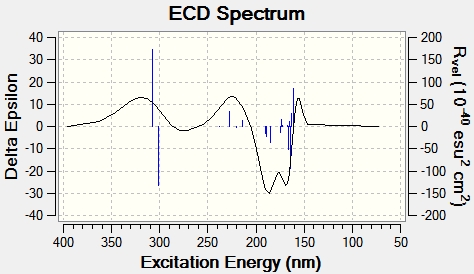
The generation of circular dichroism spectra confirms that the molecules are chiral, as only chiral molecules are CD active. A positive CD signal, as predominantly shown in figure 19, left circularly polarised light is absorbed more than right circularly polarised light. A negative CD signal, as mainly seen in figure 20, suggests right circularly polarised light is absorbed more than left circularly polarised light. This therefore suggests circular dichroism is also a successful technique in determining which isomer is present, as they have opposing absolute configurations.

Conclusion

In conclusion, all techniques shown above may be used to distinguish between the two regioisomers. Infrared spectroscopy, although producing different peaks, showed a smaller difference between the two isomers. It also showed a relatively large difference between the computed peaks and literature, suggesting the method is not completely accurate. The errors would have to be fully established to establish with certainty, which isomer is present. For ¹³C NMR, optical rotation and circular dichroism, the largest differences between the two isomers was shown, and they would therefore be the best methods to determine which isomer is present.

Overall Conclusion

The results in this module show the power of several computational methods such as MM2/MMFF94/MOPAC and Gaussian DFT based methods. Although MM2 was useful for calculating total energies for simple systems such as the products of the dimerisation of cyclopentadiene, it was not as accurate when determining the energy of more complex systems, such as the glycosidation intermediates. MM2 was unable to cope with the oxonium ion and was unable to create theoretical bonds. MOPAC/PM6 on the other hand proved to be more accurate for complex systems, at it was able to predict the formation of a new bond by minimising the energy.

In the mini-project section, Gaussian DFT based computational methods proved to be very successful in generating ¹³ C NMR, IR and CD spectra as well as optical rotation measurements that mostly corresponded to literature.

Computational methods therefore seem extremely useful in explaining and confirming the selectivity in a particular reaction, and with increasing improvement of the modelling systems, more accurate and reliable results will be obtained.