Rep:Mod:SYM1111
Introduction
In this set of computational experiments, transition structures on potential energy surfaces for the Cope rearrangement and Diels Alder cycloaddition reactions will be characterised. The most stable structure (lowest energy) of the transition states of the molecules will be found. For the Cope rearrangement, we are interested to know if the reaction undergoes a chair or boat transition state. As for the Diels Alder cycloaddition reaction, we are interested to find the more stable (ie lower energy) product - either the exo or endo product. A series of calculations were done to provide answers to these questions above.
The Cope Rearrangement
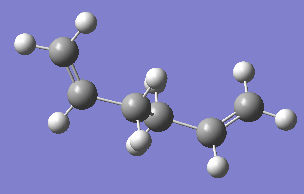
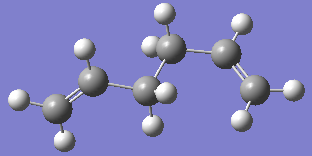
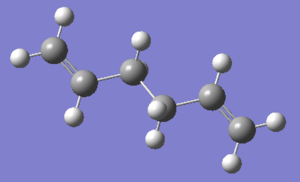
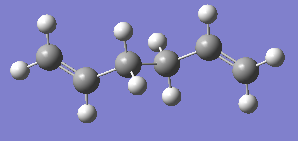
1,5-hexadiene
| antiperiplanar conformation | gauche conformation |
|---|---|
|
|
The two images above are Guassview images of optimised 1,5-hexadiene in different conformations.
Antiperiplanar conformation
Optimising the structure at HF/3-21G level of theory (Job type: Optimisation) yields -231.69253528 a.u. of energy. Using the "symmetrize" function, the molecule was assigned Ci point group.
Gauche conformation
I would expect the gauche conformation to have a higher energy than the antiperiplanar conformation. This is because the antiperiplanar conformation is free from torsional strain, while in the gauche conformation, there will be steric clashes in the alkyl groups.
Optimising the structure at HF/3-21G level of theory (Job type: Optimisation) yields -231.68771610 a.u. of energy. Using the "symmetrize" function, the molecule was assigned C2 point group.
The prediction of the gauche conformation being higher in energy is confirmed via the calculations above.
Prediction of lowest energy molecule
I would expect that the lowest energy conformation of 1,5-hexadiene is in the antiperiplanar conformation.
| |
||
 |
Optimising the structure at HF/3-21G level of theory (Job type: Optimisation) yields -231.69260235 a.u. of energy. Using the "symmetrize" function, the molecule was assigned C2 point group. | |
 |
Optimising the structure at HF/3-21G level of theory (Job type: Optimisation) yields -231.69097054 a.u. of energy. Using the "symmetrize" function, the molecule was assigned C1 point group. | |
 |
Optimising the structure at HF/3-21G level of theory (Job type: Optimisation) yields -231.68961573 a.u. of energy. Using the "symmetrize" function, the molecule was assigned C1 point group. | |
 |
Optimising the structure at HF/3-21G level of theory (Job type: Optimisation) yields -231.68907062 a.u. of energy. Using the "symmetrize" function, the molecule was assigned C2h point group. |
From the four predicted structures, Prediction 1 has the lowest energy conformation.
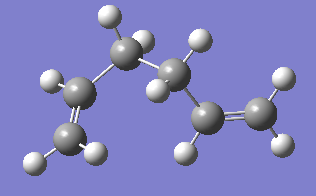
Identification of structures
The structures above are compared with those in Appendix 1.
In part (a), the structure is anti2 conformer.
In part (b), the sturcture is gauche1 conformer.
Prediction 1 is anti1, prediction 2 is anti4, prediction 3 is gauche6, and prediction 4 is anti3.
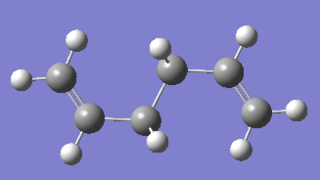
Optimising anti2 conformation of 1,5-hexadiene
| HF/3-21G | B3LYP/6-31G* |
|---|---|
|
|
HF/3-21G level of theory
Optimising the structure at HF/3-21G level of theory yields -231.69253516 a.u. of energy. Using the "symmetrize" function, the molecule was assigned Ci point group. Comparing with the table given in the notes, the structure above have the same point group, and the energy was given to be -231.69254 a.u., similar to that from the optimisation done.
B3LYP/6-31G* level of theory
Optimising the structure at B3LYP/6-31G* level of theory (Job type: Optimisation, Method: DFT) yields -234.55969661 a.u. of energy. Using the "symmetrize" function, the molecule was assigned Ci/C1 point group.
Comparing with the HF/3-21G calculation, the final energy differs by 0.13283855 a.u. The structure being optimised with HF/3-21G has a lower energy than the one being optimised with B3LYP/6-31G*.
Frequency calculation, IR spectrum and thermochemistry data
From the optimised B3LYP/6-31G* structure, a frequency calculation at the same level of theory was run (Job type: Frequency). The infrared spectrum obtained is shown below:
Sum of electronic and thermal Energies= -234.408954 a.u
Sum of electronic and thermal Enthalpies= -234.408010 a.u
Optimising the "Chair" Transition Structure
Optimising the allyl fragment (CH2CHCH2)
Optimising the structure at HF/3-21G level of theory (Job type: Optimisation) yields -115.82303995 a.u. of energy.
Optimising the transition state of the chair conformation
Using HF/3-21G level of theory(Job Type: Opt+Freq, Optimisation to TS (Berny), Calculate force constants once, additional keyword: Opt=NoEigen), the guessed transition state of the chair conformation was optimised. (Figure 1)
An animation of how the bonds move to form the chair transition state of the Cope Rearrangement is shown below:
The optimisation was successful and a transition state was observed. The imaginary frequency obtained was -818.01cm-1, which is an indication of the presence of a transition state.
Bond forming bond lengths obtained via this calculations are 2.02019Å and 2.02038Å.
Optimising the transition structure using the freeze coordinate method
Using HF/3-21G level of theory(Job Type: Opt+Freq, Optimisation to TS (Berny), Calculate force constants once, additional keyword: Opt=NoEigen), and Redundant Coord Editor (Bond, Add, Freeze coordinate options selected), the guessed transition state of the chair conformation was optimised.
After completing the job above, the bond forming/breaking distances are fixed to 2.2Å. This will be optimised using the subsequent steps using the Redundant Coord Editor. One of the bonds previously frozen was chosen (Bond, Derivative options were chosen) and this was repeated for the other frozen bond as well. The normal guess Hessian modified was used to include information of the two coordinates being differentiated (Job type: Never calculate force constants, keeping the rest of the settings same as above). The optimised transition state of the chair conformation using the freeze coordination method is shown (Figure 2)
Bond forming bond lengths obtained via this calculations are 2.02095Å and 2.02053Å.
The bond forming lengths of the two methods above are almost the same - approximately 2.02Å to 3 significant figures.
Optimising the "Boat" Transition Structure
Using the QST2 method for optimisation
Using the anti2 molecule previously optimised, further analysis was done to obtain the boat transition structure. Using the QST2 calculation (Job Type: Opt+Freq, TS(QST2),the optimised transition state of the boat conformation was obtained.
However, this method does not work. The transition state obtained was distorted in a way which was not what we would expect. This is because when the calculation was linearly interpolated between the two structures, the top allyl fragment was translated and the possibility of rotation around central bonds was not considered.
Modifications to the QST2 method
Reactant and product geometries were thus modified so that they are closer to the boat transition states. The dihedral angle of the second carbon to the fifth carbon (C-C-C-C) was set to 0 degrees, and the second to forth carbon (C-C-C) and third to fifth carbon (C-C-C) was reduced to 100 degrees.
| Reactant | Product |
|---|---|
|
|
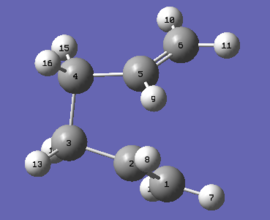
The QST2 calculation was then set up again. Now, we obtain the right boat transition structure:
From these calculations, there was only one negative frequency value obtained (-840.01cm-1). The infrared spectrum obtained is shown below:
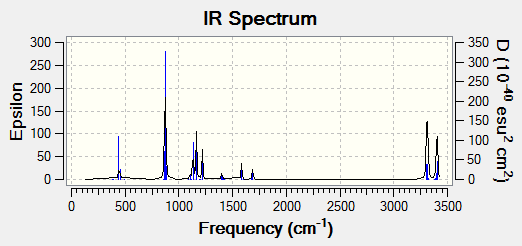
An animation of the boat transition state is shown below:
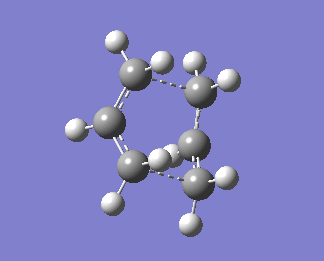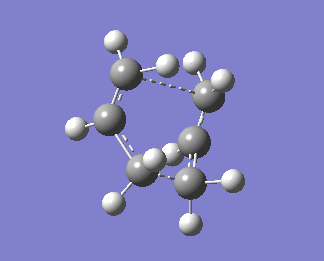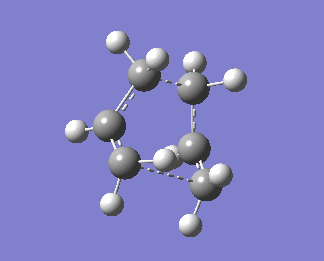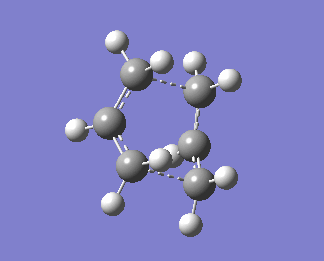
Bond forming bond lengths obtained via this calculations are 2.13983Å and 2.14071Å. One imaginary frequency was obtained, -840.01cm-1. This imaginary frequency is an indication of the transition state.
Intrinsic Coordination Method
This method follows the minimum energy path from a transition structure down to its local mimum on a potential energy surface.
Using HF/3-21G level of theory(Job Type: IRC, compute in forward direction, always calculate force constants, number of points = 50), the guessed transition state (predicted to be the minimum energy) of the chair conformation was calculated.
Prediction of the minimum energy transition state: (Note: Both images are the same molecule at different angles)
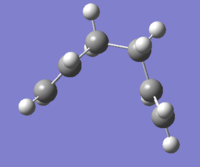
Comparing to the table of values in the script, this molecule was found to be gauche2, with energy value of -231.69157825 a.u..
An animation of the gauche2 molecule is shown below:
An IRC graph was obtained:
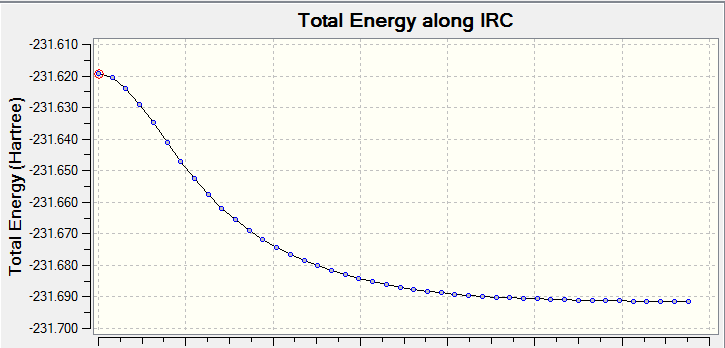
Further analysis
Further analysis was done using three different methods to confirm that the prediction molecule has reached a minimum geometry.
Method one: Last point on IRC was taken and a normal minimization was run
This methods yields the same structure of gauche2 and same energy value as well.
Method two: IRC restarted and number of points was set to 200
This methods yields the same structure of gauche2 but a slightly different energy was obtained, -231.69157800 a.u..
Method three: Force constants was computed at every step
This methods yields the same structure of gauche2 as well. but this time the energy value obtained was -231.69166702 a.u., which is closer in value to the one given in the script, -231.69167 a.u..
Calculation of activation energies of the chair and boat transition states
Starting from the HF/3-21G optimised structures, both chair and boat transition structures were reoptimised using the B3LYP/6-31G* level of theory and frequency calculations were carried out (Job Type: Opt+Freq, TS (Berny)).
The two levels of theory yield the same geometry but different energies. In this experiment, low level of theory was used to map the potential energy surface first before reoptimising at the higher level.
A table showing the summaries of these energies are shown below:
Summary of energies (in hartree)
| HF/3-21G | B3LYP/6-31G* | |||||
|---|---|---|---|---|---|---|
| Electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | Electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | |
| at 0 K | at 298.15 K | at 0 K | at 298.15 K | |||
| Chair TS | -231.618642 | -231.462513 | -231.458613 | -234.505467 | -234.362677 | -234.356762 |
| Boat TS | -231.604612 | -231.455946 | -231.442497 | -234.492891 | -234.344098 | -234.338795 |
| Reactant (anti2) | -231.692535 | -231.539539 | -231.532566 | -234.559704 | -234.416244 | -234.408954 |
Summary of activation energies (in kcal/mol)
| HF/3-21G | HF/3-21G | B3LYP/6-31G* | B3LYP/6-31G* | Expt. | |
| at 0 K | at 298.15 K | at 0 K | at 298.15 K | at 0 K | |
| ΔE (Chair) | 48.33 | 46.41 | 32.75 | 33.61 | 33.5 ± 0.5 |
| ΔE (Boat) | 52.46 | 56.52 | 45.27 | 44.03 | 44.7 ± 2.0 |
Note that *1 hartree = 627.509 kcal/mol
The activation energies using B3LYP/6-31G* method is rather close to that obtained from experiments.As B3LYP/6-31G* is a higher level of theory, reoptimising molecules using HF/3-21G level of theory would give a result closer to the actual value, which is why using the latter method gives values which differ by quite a significant amount from the experimental values.
Also, it can be concluded that the activation energy for the molecule to be in the boat transition state is much higher than that of the chair transition state, hence it is more likely for the reaction to undergo a chair transition state as the barrier of the reaction is lower.
Diels-Alder Cycloaddition
Optimizing cis-butadiene
Optimising the structure at HF/3-21G level of theory (Job type: Optimisation, Method: Semi-empirical, AM1) yields 0.04879719 a.u. of energy. Using the "symmetrize" function, the molecule was assigned C2v point group.
| HOMO | LUMO |
|---|---|
|
|
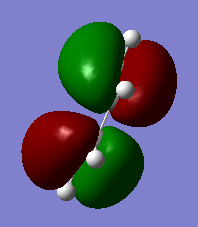
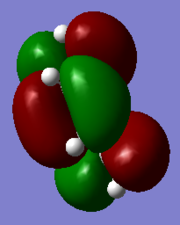
HOMO is symmetric while LUMO is antisymmetric.
Computation of the Transition State geometry for the prototype reaction and an examination of the nature of the reaction path
Ethylene and cis-butadiene are both optimised separately at HF/3-21G level of theory (Job type: Optimisation, Method: Semi-empirical, AM1). They were then put together for optimisation of the transition state via [4+2] cycloaddition process.
Method 1: Freeze coordinate method
Optimising the structure at HF/3-21G level of theory (Job type: Optimisation, Method: Semi-empirical, AM1) yields 0.11431503 a.u. of energy.The bond lengths of the partly formed σ C-C bonds are 2.11850Å and 2.11929Å.
| HOMO | LUMO |
|---|---|
|
|
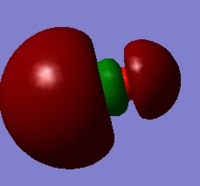
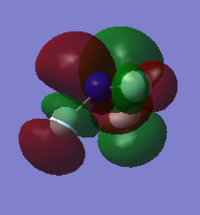
Both HOMO and LUMO are antisymmetric.
Method 2: Redundant coordinate method
One of the bonds previously frozen was chosen (Bond, Derivative options were chosen) and this was repeated for the other frozen bond as well. The normal guess Hessian modified was used to include information of the two coordinates being differentiated (Job type: Never calculate force constants, keeping the rest of the settings same as above). This method yields 0.11314896 a.u. of energy for the molecules. The bond lengths of the partly formed σ C-C bonds are 2.12492Å and 2.08430Å.
Method 3: QST2 method
Using the QST2 calculation (Job Type: Opt+Freq, TS(QST2)),the optimised transition state was obtained. The bond lengths of the partly formed σ C-C bonds are 2.12105Å and 2.11713Å.
| HOMO | LUMO |
|---|---|
|
|
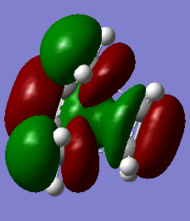
Both HOMO and LUMO are antisymmetric.
The infrared spectrum obtained via the calculations are shown below:
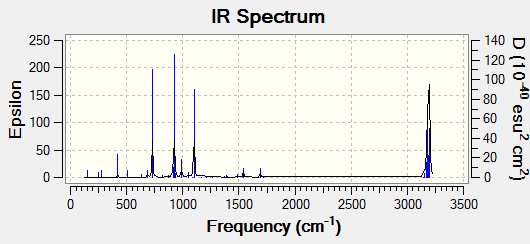
An animation of the transition state using QST2 is shown:
There is only one imaginary frequency value obtained in this calculation, -956.57cm-1. The formation of two bonds are synchronous. The lowest positive frequency is 147.23 cm-1. Imaginary frequencies are indicative of a transition state, while positive frequencies represent a minumum energy of the reaction.
Discussion
The structure of the transition state depicts a distorted tetrahedral about the C-C bonds which are in the process of forming. This is because there is a change in hybrisation and thus angles between the atoms - initially the carbons were sp2 hybrised (double bonds), but during the transition state, it gradually becomes sp3 hybridised (single bonds). Here, ethene approches cis-butadiene in a parallel manner, which will allow for maximum orbital overlap.
Typically, sp2 bond lengths are 1.34Å while sp3 bond lengths are 1.54Å. The Van der Waals radius of carbon is 1.70Å. The C-C bond length of a partly formed σ C-C bond in a transition state is much longer than both a single and double bond. However, this partly formed C-C bond length is still shorter than the bond length of 2 carbons which are not interacting. This suggests possibility of interactions and attractive forces between the two carbons (which are forming the bond for the cycloaddition reaction) which then gradually forms a bond in the end for completion of reaction.
The HOMO at the transition structure is antisymmetric. This cycloaddition reaction involves the HOMO of the diene (1,3-butadiene) and LUMO if the dienophile (ethene). Both the HOMO and LUMO of the two compounds are antisymmetric and are close in energy levels thus have very efficient orbital overlap, hence the reaction is allowed.
This reaction will be more favourable if the dienophile has an electron withdrawing substituent (such as CO2Me - as shown in the later section on "Additional Investigation", or maleic anhydride - as shown in the next section of this page) and the diene has electron donating groups attached to it so that it is more electron rich. Adding an electron withdrawing group on the dienophile will lower its LUMO energy, hence making it much closer to the HOMO orbital of the diene. Thus, the energy of the resultant bonding orbital will decrease, and hence making the two reactants much more reactive than initial.
Study of regioselectivity of the Diels Alder Reaction
Cyclohexa-1,3-diene and maleic anhydride were both optimised separately at HF/3-21G level of theory (Job type: Optimisation, Method: Semi-empirical, AM1). They were then put together for optimisation of the transition state via Diels Alder reaction.
| Cyclohexa-1,3-diene after optimisation | Maleic anhydride after optimisation |
|---|---|
|
|
Endo Product
Using the QST2 calculation (Job Type: Opt+Freq, TS(QST2)),the optimised transition state was obtained. This method yields an energy of -0.05150411 a.u. for the molecule.
The C-C bond lengths and distances of interest are shown below (Bond lengths are given in angstroms). The bond forming lengths are 2.16113Å and 2.16442Å.
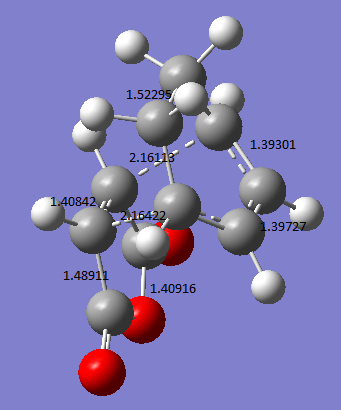
An animation of the transition state process is shown below. Only one imaginary frequency value was obtained, -811.78cm-1. This an indicative of a transition state, which is the endo transition state in this case.
Exo Product
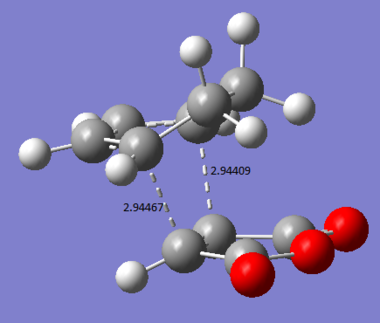
Using the QST2 calculation (Job Type: Opt+Freq, TS(QST2)),the optimised transition state was obtained. This method yields an energy of -0.05041960 a.u. for the molecule.
The C-C bond lengths and distances of interest are shown below. (Bond lengths are given in angstroms)
An animation of the transition state process is shown below. Only one imaginary frequency is obtained, -805.55cm-1. This is an indication of the presence of a transition state, which is the exo transition state in this case.
Some discussion
For symmetric dienophiles such as ethene and maleic anhydride used in this set of experiments, each end of the double bond can act as an electrophilic site for attack by the diene with equal probability. As long as the diene and dienophile are aligned properly for the formation of new C-C bonds (cycloaddition), the bonds are formed very quickly, hence the Diels-Alder reaction is synchronous.
From literature2, it is also suggested that for a reaction with electron-rich dienes and electron-poor dienophiles, the reaction undergoes an asynchronous mechanism.
Exo vs endo transition states
Although the exo product is more stable, the endo product is preferentially formed. This is because in this case, the exo form is more strained than the endo form. Although the endo product is less stable (kinetic product), it is still preferentially formed. This is because there is a bonding interaction between the carbonyl groups of the dienophile and the developing π bond at the back of the diene. This is the result of secondary orbital overlap effect - the stabilisation of the endo product. Secondary orbital overlap is also present in the exo transition state but there is much less effecient overlap, hence resulting in the preferential formation of the endo transition state.
Exo vs endo structural differences
Exo: The electronegative -(C=O)-O-(C=O)- fragment is pointing away from the diene in order to reduce steric clashes. However, because it points away, it loses out on additional stabilisation (secondary orbital overlap interactions) and thus is less preferntially formed in this case.
Endo: The electronegative -(C=O)-O-(C=O)- fragment is directly above/below the diene and hence is stabilised by secondary orbital overlap interactions.
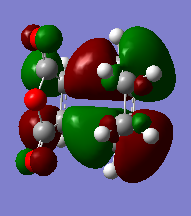
Nodal area of exo and endo HOMOs
The size of the nodal area between the -(C=O)-O-(C=O)- fragment and the remainder of the system is a gauge of the degree of stabilisation and bonding interactions of the exo and endo transition states. In both the exo and endo HOMOs, there are nodal lobes around the oxygen atom in the -(C=O)-O-(C=O)- fragment.
In the exo transition state, there is a large nodal area between the -(C=O)-O-(C=O)- fragment and the remainder of the system. This is because the -(C=O)-O-(C=O)- fragment is pointed away from the diene (as mentioned above describing the structure of the exo transition states), hence it is unlikely for any interaction between the two fragments to be possible. There is a small nodal area for the endo transition state, hence indicating more bonding interaction in the middle portions between the carbons in the -(C=O)-O-(C=O)- fragment and the carbons (those not involved in bond formation) of the diene. As the diene is directly above/below the -(C=O)-O-(C=O)- fragment (unlike in the exo case where the two fragments are pointed away), there is a higher chance of interaction and thus resulting in a smaller nodal area.
Additional Investigation of a published example
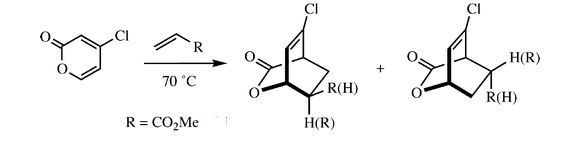
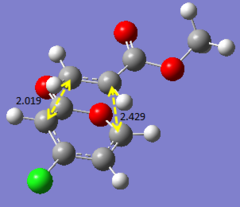
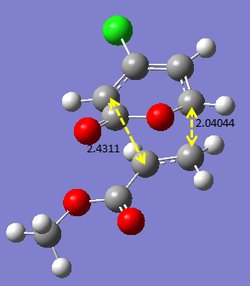
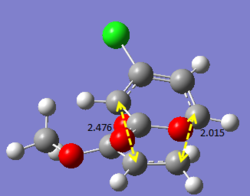
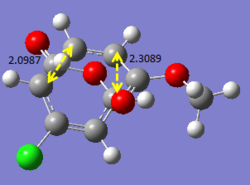
Additional investigation is done on a published example [[1]] in order to find the lowest energy transition state of the molecule. As an asymmetric alkene is involved, there are two possible endo and exo products each, resulting in four possible products in total. The following calculations will show the structures and bond lengths of the transition states, and from there the lowest energy transition state will be found.
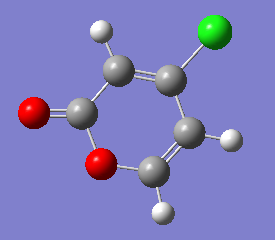
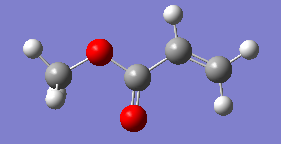
Optimising 4-Chloro-2(H)-pyran-2-one and methyl acrylate
4-Chloro-2(H)-pyran-2-one and methyl acrylate were both optimised separately at HF/3-21G level of theory (Job type: Optimisation, Method: Semi-empirical, AM1). They were then put together for optimisation of the transition state via Diels Alder reaction.
| 4-Chloro-2(H)-pyran-2-one after optimisation | methyl acrylate after optimisation | |
|---|---|---|
|
|
After optimisation, the energy of 4-Chloro-2(H)-pyran-2-one was found to be -0.08307721 a.u., while the energy of methyl acrylate was found to be -0.11175406 a.u..
Summary of results
The transition states were first calculated via QST2 method (semi-empirical, AM1) and then reoptimised using DFT method (B3LYP/6-31G*). It was observed that the QST2 gives an approximate value of the bond forming bond lengths, and with reoptimisation, a more accurate bond forming bond length is obtained, which yields values rather similar to that in the published example. The four products (EXO5, EXO6, ENDO5, ENDO6) are labelled as in the published paper. The results obtained are summarised below. (Bond lengths are given in terms of angstroms.)
| |
|||||
 |
 |
 |
 |
||
 |
 |
 |
 |
||
 |
 |
 |
 |
||
DFT: -511.52 |
DFT: -502.08 |
DFT: -858.55 |
DFT: -499.52 |
||
DFT: -1109.3926 |
DFT: -1109.3952 |
DFT: -1109.3899 |
DFT: -1109.3912 |
The bond lengths obtained via these optimisations are compared with that from literature. The values obtained using the computational methods are in fact very close to what was obtained in literature, hence indicating that the optimisation method used is rather accurate. From the energy values obtained, it is concluded that ENDO5 has the lowest energy and hence is the lowest energy transition state. Thus, it is most likely that for the reaction above, the transition will under go the ENDO5 structure. This is also confirmed from literature, where the enthalpy change of formation is the smallest for the ENDO5 structure.
It is also noted that the energies of the endo transition states are lower than the exo transition states, hence indicating that the endo transitions are in general more stable than the endo ones.
Some Discussion
For asymmetric dienes and dienophiles, there is generally great regioselectivity. In the example above where the dienophile has an electron withdrawing group attached to it (electron-poor dienophile), the most nucleophilic atom in the diene is bonded to the most electrophilic atom in the diene preferentially. It is also good to note that Diels-Alder reaction has great stereoselectivity as well - trans-substituted dienophiles results in trans-substituted cyclohexes, the same goes for cis-substituted dienophiles.
Further Discussion
In this exercise, we focus on HOMO/LUMO interactions to find out whether a reaction is allowed (symmetric/antisymmetric orbitals), and then proceed to calculate the energies of the transition states to investigate the most likely pathway in which the final structure is formed.
However, there are limitations to the frontier orbital theory. In a compound with multiple functional groups and conjugation, the HOMO is likely to span across a large portion of the molecule and not only to a particular position - this makes it difficult to analyse the results obtained. Also, if the reaction occurs in compounds with aromatic systems, the aromatic system will prefer to remain its original state as any reactivity (such as deprotonation) will cause it to lose its resonance stabilisation.
In addition to the factors listed above, there are several other factors that might affect the calculation of the Diels-Alder transition states.
1. Type of substituent
When the dienophile has bulky substituents attached to it, the exo product will be preferentially formed, as forming the endo product will cause huge steric clashes and unfavourable interactions/repulsions. Also, as mentioned previously, the reaction is favoured when electron withdrawing groups are attached to the dienophile and electron donating groups are attached to the diene - this reduces the HOMO/LUMO gap, hence activation energy of the reaction can be lowered.
2. Temperature - Thermodynamic or kinetic control
Under thermodynamic conditions, the exo product will be preferentially formed as it is the more stable product. However, under kinetic conditions, the endo product will be preferentially formed.
Conclusion
The calculations were completed using different methods with results and analysis shown in the previous sections. As for the additional investigations done, values obtained from the optimization showed good agreement with literature values. The use of computational methods are thus extremely useful for prediction of reactions. Although the values obtained in this set of experiment are rather accurate, more methods and higher level of theories can be used to confirm the value of the data obtained.
References
1. Kamyar Afarinkia, Michael J. Bearpark, Alexis Ndibwami. "Computational and Experimental Investigation of the Diels-Alder Cycloadditions of 4-Chloro-2(H)-pyran-2-one" JOC Articles. 2003 (http://dx.doi.org/10.1021/jo0348827)
2. Molecular Orbitals in Conjugated Systems. Department of Chemistry and Biochemistry at UC Santa Barbara, 2011. Source accessed on: 29/10/2013 (http://web.chem.ucsb.edu/~kalju/chem109C/DielsAlder.html)