Rep:Mod:SYD96

Optimization of Molecules

Optimization of NH₃

General Data

Parameter	Value	Unit
Molecule	NH3
Calculation Type	OPT+FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d.p)
E(RB3LYP)	-56.55776762	a.u
RMS Gradient Norm	0.000000485	a.u.
Point Group	C3V
Bond Length	1.01865	Å
Bond Angle	105.759	deg.

Item	Value	Threshold
Maximum Force	0.000004	0.000450
RMS Force	0.000004	0.000300
Maximum Displacement	0.000072	0.001800
RMS Displacement	0.000035	0.001200

NH3

The optimization file is liked to here

Vibrational modes

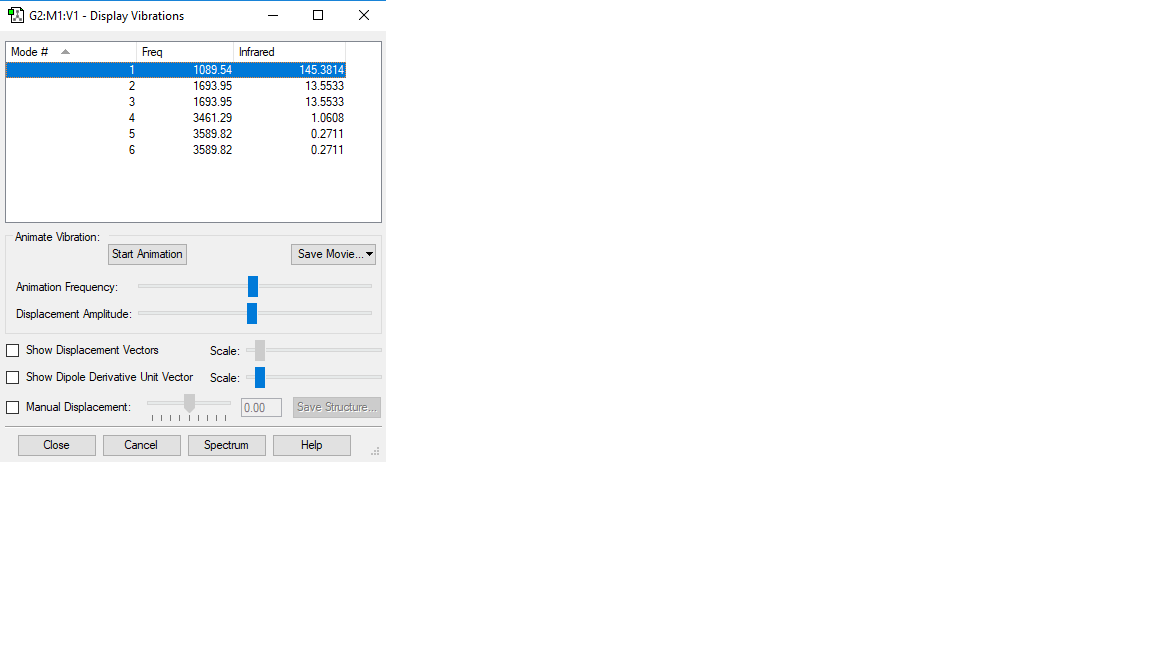
According to the 3N-6 we would expect to see 6 vibrational modes. Degenerate modes have the same energy, therefore in this case, modes 2 and 3 and modes 5 and 6 are degenerate. Vibration modes 1,2,3 are bending modes, whereas modes 4,5,6 fall into the stretching mode category. Vibration mode 4 is very symmetric. Mode 1 is known as the "umbrella mode". Since there are four different distinct energy levels, we would expect to see four different bands in an experimental spectrum of gaseous ammonia. However, two of them are too low so only two bands will be seen.

Charge distribution

Due to the relatively high electronegativity of N compared to H, we expect the charge of the N atom to be negative in contrast to the charge of the H atoms, which we expect to have a positive charge. Moreover, the fact that ammonia molecules form hydrogen bonds, something that requires a difference in relative charge within the molecule. This is confirmed by the calculations which determined the value for the charge of the N atom at -1.125 and the charge for the H atom at 0.375.

Optimization of N₂

General Data

Parameter	Value	Unit
Molecule	N2
Calculation Type	OPT+FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d.p)
E(RB3LYP)	-109.52412868	a.u
RMS Gradient Norm	0.00000060	a.u.
Point Group	D*H
Bond Length	1.10550	Å
Bond Angle	N/A	deg.

Item	Value	Threshold
Maximum Force	0.000001	0.000450
RMS Force	0.000001	0.000300
Maximum Displacement	0.000000	0.001800
RMS Displacement	0.000000	0.001200

N2

The optimization file is liked to here

Vibrational modes

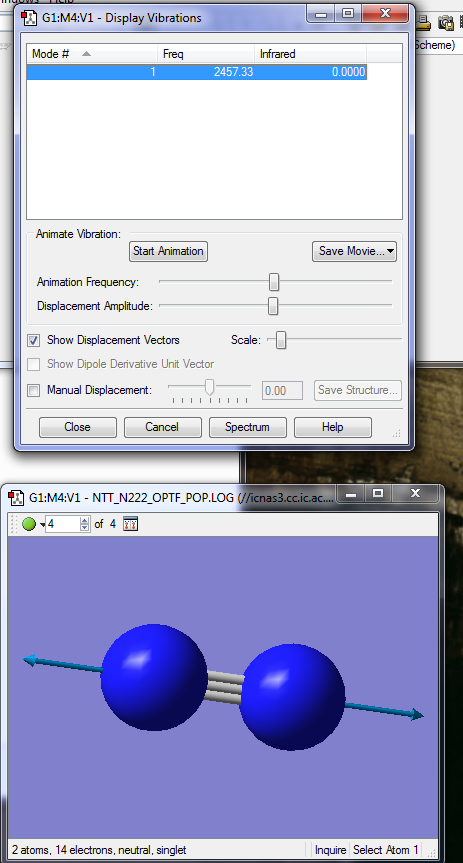
The nitrogen molecule is linear, therefore the number of vibrational modes is determined by the 3N-5 rule. We should, as a result, expect to see only one vibrational mode, which is confirmed as shown in the following picture. The vibrational mode is a symmetrical stretch.

Charge distribution

The nitrogen molecule consists of two identical nitrogen atoms. Therefore, electrons are distributed equally and the charge will be equal to zero, as we see no dipole.

Optimization of H₂

General Data

Parameter	Value	Unit
Molecule	H2
Calculation Type	OPT+FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d.p)
E(RB3LYP)	-1.17853936	a.u
RMS Gradient Norm	0.00000017	a.u.
Point Group	D*H
Bond Length	0.074279	Å
Bond Angle	N/A	deg.

Item	Value	Threshold
Maximum Force	0.000000	0.000450
RMS Force	0.000000	0.000300
Maximum Displacement	0.000000	0.001800
RMS Displacement	0.000001	0.001200

NH3

The optimization file is liked to here

Vibrational modes

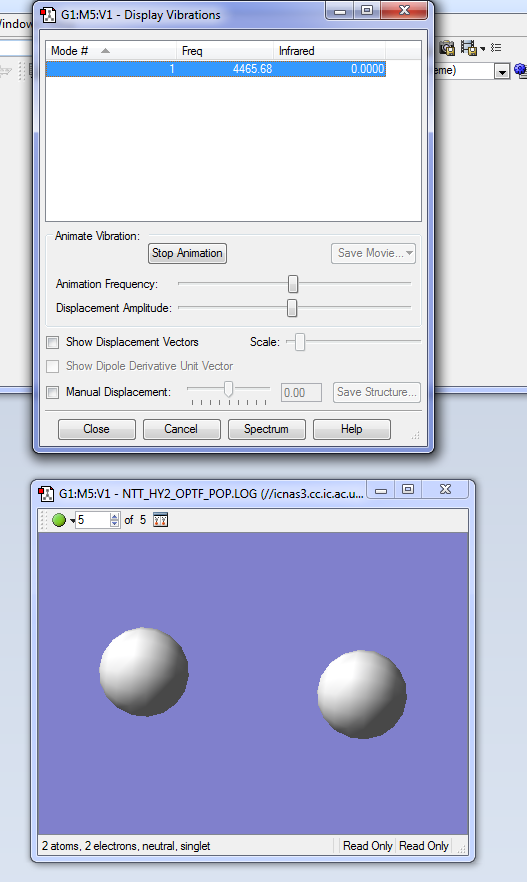
The hydrogen molecule is linear, therefore the number of vibrational modes is determined by the 3N-5 rule. We should, as a result, expect to see only one vibrational mode, which is confirmed as shown in the following picture.

Charge distribution

The hydrogen molecule consists of two identical hydrogen atoms. Therefore, electrons are distributed equally and the charge will be equal to zero, as we see no dipole.

Reaction energies

• E(NH₃)= -56.55776762 a.u
• 2*E(NH₃)= -113.11553524 a.u
• E(N₂)= -109.52412868 a.u
• E(H₂)= -1.17853936 a.u
• 3*E(H₂)= -3.53561808
• ΔE=2*E(NH₃)-[E(N₂)+3*E(H₂)]= -0.05578848 a.u = -146.4726653977 KJ/mol

The energy, therefore, is 146.48 KJ/mol. Since the gaseous ammonia formed by the reaction is lower in energy than the reactants it is more stable. This is also supported by the fact that the reverse reaction does not happen, meaning that it is not energetically favorable.

Optimization of CH₄

General Data

Parameter	Value	Unit
Molecule	CH4
Calculation Type	OPT+FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d.p)
E(RB3LYP)	-40.52401404	a.u
RMS Gradient Norm	0.00003263	a.u.
Point Group	TD
Bond Length	1.09197	Å
Bond Angle	109.5	deg.

Item	Value	Threshold
Maximum Force	0.000063	0.000450
RMS Force	0.000034	0.000300
Maximum Displacement	0.000179	0.001800
RMS Displacement	0.000095	0.001200

CH4

The optimization file is liked to here

Vibrational modes

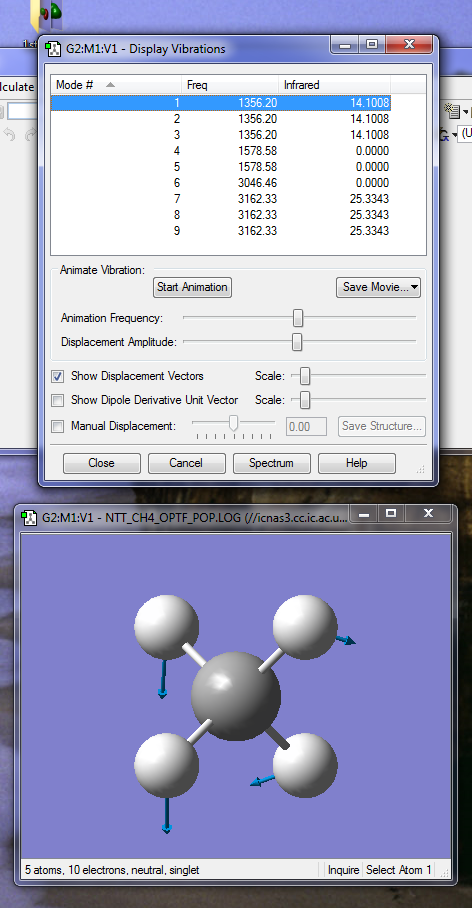
According to the 3N-6 we would expect to see 9 vibrational modes. Degenerate modes have the same energy, therefore in this case, modes 1, 2 and 3, modes 4 and 5 and modes 7, 8 and 9 are degenerate. Vibration modes 1,2,3,4,5 are bending modes, whereas modes 6,7,8,9 fall into the stretching mode category. Vibration mode 6 is very symmetric. Two bands will be seen in the spectrum of gaseous methane.

Charge distribution

Since carbon is slightly more electronegative than hydrogen, we expect the carbon atom to have a slightly negative charge and the hydrogen atoms to have a smaller positive charge. This is supported by the GaussView calculations which determine the charge for carbon to be -0.930 a.u. and the charge for the hydrogen atoms to be 0.230 a.u.

Molecular orbitals

The four bonding orbitals of methane can be seen below. They are a result of overlap between 2s and 2p atomic orbitals from carbon and the four 1s atomic orbitals of hydrogen. The first one is equally distributed around the molecule, indicating electrons equally shared between the carbon and four hydrogen atoms. In the next three, which are degenerate and higher in energy than the first (-0.01429548 a.u. compared to-0.02539377 a.u. for the first one), the only difference is their orientation. We can see a phase change (red and green) which decreases the net bonding. All of the MOs are delocalized, but all of them show high electron densities between carbon and hydrogen.

Below is a picture of the lowest energy non-bonding orbital, which empty and does not affect energy. If we added an electron to this orbital, bonding between carbon and hydrogen will be decreased.