Rep:Mod:STrimmer2

Module 2

Samuel Trimmer

Introduction

This module looks into the basics of computational chemistry. The tasks performed throughout show the reasoning behind the methods used and the settings chosen for certain calculations. This module progresses from module 1 in that it uses gaussian calculations to study the reactivity of a molecule rather than just which product is most stable. This module moves away from small organic molecules to larger inorganic molecules which require different settings. In order to optimise these larger more complex molecules and study their orbitals the schrodinger equation has to be solve.

In the project itself borane is optimised and its frequency, molecular and natural bonding orbitals are studied. It is then compared with the optimisation of thallium bromide which requires different treatment, in the form of pseudo-potentials , because of the heavier atoms involved. Following this the cis/trans isomerisation of Mo(CO)₄(PCl₃)₂ is studied. The vibrations are looked at in detail to ascertain why the IR spectrum's differed for the two isomers.

Finally this module consists of a mini project in which I chose to look at the geometry of d8 complexes, in particular NiCl₄ and NiCN₄. The aims of this project are to see if the computational methods predict the geometries to be the same as the literature. Furthermore the project aims to look into the reactivity of the complexes by studying the nature of the molecular orbitals produced.

BH₃ Creation and Optimisation

Boroane is a trigonal planar molecule with an sp2 hybridised boron which also has an empty p orbital perpendicular to the plane. This molecule was created in gaussview and the hydrogen boron bond lengths were set to 1.5 angstroms.

Once this molecule had been created its geometry was optimised by a gaussian calculation. The method used for the optimisation is called DFT-B3LYP with a 3-21G basis set. These calculations were run and the results of the optimisation are shown below.

BH₃ Geometry Optimisation Summary

File Type	.log File	Pentahelicene
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	3-21G
Final Energy/Hartree a.u.	-26.46
Final Gradient	0.00000285
Dipole Moment	0.00
Point Group	D3H

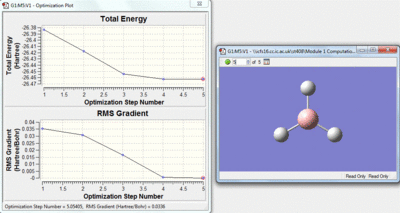
This method is a iteration process. The initial molecule will have a certain amount of attractive and repulsive forces due to its geometry. A separate geometry is then tried by the calculation if this is lower in energy the molecule will then change to this geometry, if however the new geometry is not lower in energy a different one will be tried by the calculation. Over the optimisation process the energy gap between each geometry will decrease and as this happens the rate of the change of energy with respect to the iterations will approach zero. The Rate of energy change with respect to the iterations is the gradient of the top graph shown below, the bottom graph shows how this gradient changes.

Optimisation of Borane

Stage 1	Stage 2	Stage 3

Stage 4	Stage 5

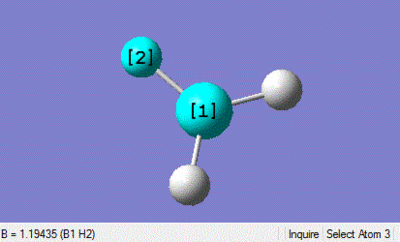
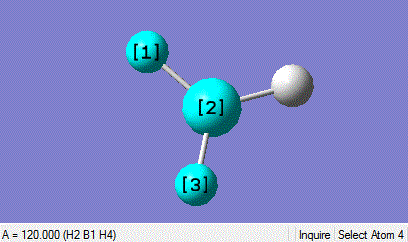
This DFT-B3LYP optimisation using the basis set 3-21G gives a B-H bond length of 1.19435 angstroms and a H-B-H bond angle of 120 degrees. This is not far from the values in the literature of 1.1867 angstroms which suggests that the method for optimisation suits small molecules well.

BH₃ after optimisation

Bond legnth	Bond Angle

BH₃ Molecular Orbitals

Once the Borane molecule had its geometry optimised the molecular orbitals could now be calculated running a new gaussian calculation. The calculation was an energy calculation using the DFT-B3LYP method and the 3-21G basis set and set to calculate full natural bonding orbitals (NBO's). Below the molecular orbitals have been determined theoretically using the Linear combination of atomic orbitals.

OUTPUT FILE http://hdl.handle.net/10042/to-7025

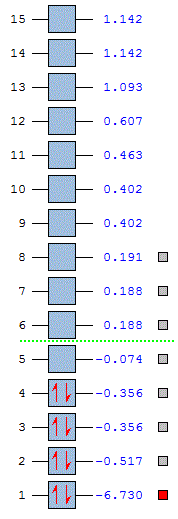
The Molecular orbital diagram above (created in Chemdraw) shows the prediction of the mixed atomic orbitals of the BH3 molecule, the calculated energy levels from an the second optimisation are tabulated below.

Molecular Orbital Optimisation of BH₃

Molecular Orbital Symmetry	Image of Calc. Orbital	Predicted Orbital	Orbital Energy
1a'1			-6.730
2a'1			-0.517
1e'			-0.356
1e'			-0.356
1a2			-0.074
3a'1			0.191
2e'			0.188
2e'			0.188

The images above show just how well the computational model works. The actual molecular orbitals calculated computationally show a much better picture of the mixing of the molecule orbitals. Furthermore they get the energy levels in the correct order and the correct relatives heights. For example in my molecular orbital diagram the 2e' and the 3a'₁ should be the other way round when looking at the computed energy levels. The orbital height is more of an educated guess in the LCAO method. Below is a image of the energies of the molecular orbitals, relative to that of a 1s atomic orbital.

Furthermore it can be seen from these orbitals that the if the LUMO were filled that the energy stabilisation would be great. This is why borane exhists as a dimer B₂H₆. This sort of insight can only be seen with the computational calculation, the LCAO method does not give as much detailed information.

BH₃ NBO Analysis

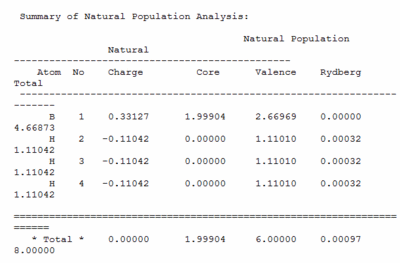
The natural bond orbitals were caluclated in the molecular orbital calculation, below the charge distribution is shown in number and colour, with red being negative and green positive.

Below is the summary of natural population file that shows the distribution of charge over the molecule. Shows the boron with the positive charge and the hydrogen's to have the negative over them.

Below are the orbital co-efficients which show how boron to be sp2 hybridised, 33% S character and 66% P character. It also shows the bond being made up of 55.5% Hydrogen and 44.5% Boron. Furthermore this output file shows the lone pair to be all in a Boron P orbital.

BH₃ Vibrational Analysis

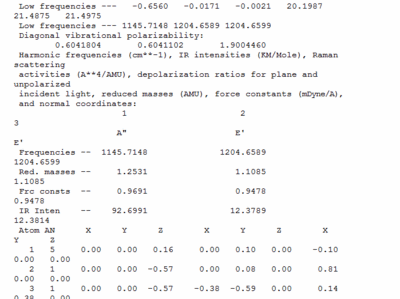
Vibrational calculations were carried out sing the geometry optimised borane molecule. The vibrational calculations are a further way of confirming that the optimised geometry is a minimum point on the potential energy surface, essentially it calculates the second derivative of the surface and if the vibrations calculated are all positive then it is a minima that has been obtained. The frequency calculation was performed using the DFT-B3LYP method and a 3-21G basis set. The output file for the calculation is shown below.

This image from the output file shows the low frequency in the vibrational analysis. If the low frequencies are an order of magnitude lower than the real frequencies then the calculations are of a good calibre, this is the case for my calculations. Furthermore all the vibrations showing a positive value indicates that the calculation has converged at the lowest minima.

Comparison of Vibrations

Vibration No.	Vibration Form	Frequency	Infrared	Symmetry D3H point Group and description
1		1145	92.7	All 3 hydrogen atoms have an in-phase vibration that is perpendicular to σh plane (A2)
2		1204	12.38	2 Hydrogen atoms bend in-phase whilst the other remains stationary, all in the σh plane (E')
3		1204	12.38	2 Hydrogen atoms rock in phase whilst the other rocks out of phase all in the σh plane (E')
4		2592	0	In phase symmetric stretch of all 3 Hydrogen atoms within the σh plane (A1')
5		2731	103.8	2 Hydrogen atoms have an asymmetric stretch in σh plane whilst the other remains stationary, the born atom rocks slightly in the σh plane as well (E')
6		2731	103.8	One hydrogen is undergoing a asymmetric stretch with respect to the other two stretching hydrogen's. The boron moves asymmetrically to the hydrogens. All the stretches are in the σh plane (E')

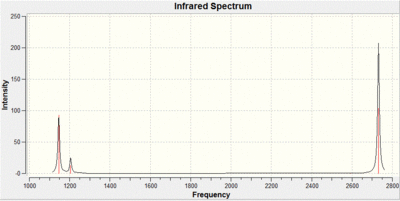
As well as calculating the motions of the vibrations the IR spectrum is also formulated, shown below.

This vibrational analysis shows that there are two sets of degenerate vibrations both, and two that are separate single vibrations and one that does not show up due to it being symmetrical.

TlBr₃ Optimisation

Thalium tribromide is a species that is much larger in comparison to the Boron Trihalide molecule. When using computational chemistry calculations the number of electrons in the molecule to be optimised has a profound effect on the method implemented and the ease at which the calculations can be carried out. Generally speaking chemistry considers the valence electrons to dominate bonding characteristics as is the case with these calculations. This allows the core of electrons to be modelled into what is called a pseudo-potential. As well as using a pseudo-potential the basis set needs to be changed for larger species. A basis set is the number of functions used to describe the molecules, for a larger molecule more functions are required in order to obtain accurate results.

The optimisation calculation was set up in gaussian using a DFT-B3LYP method with a LanL2DZ medium level basis set, the optimised structure is shown below. The point group was constrained to D3h and the tolerance increased to very tight (0.0001).

The optimisation method would seem to be a good method, and the pseudo-potential basis sets used also seem to be well suited to the calculation as the bond lengths match up well with the literature values. The bond length obtained 2.65 is similar to that of literature value 2.5, as is the bond angle 120 and the literature bond angle 120.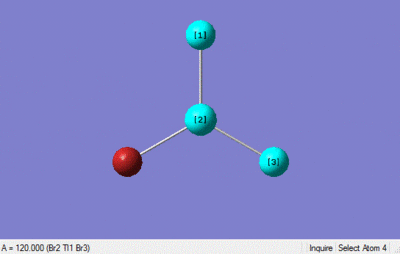

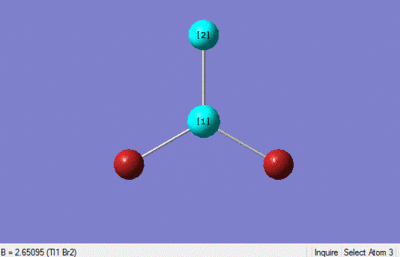
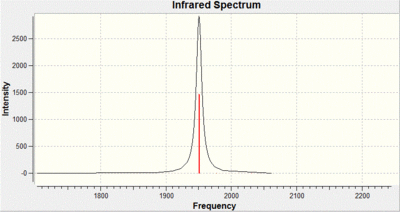
The frequency analysis was then carried out in order to check that a minima was obtained. Furthermore the vibrational analysis is carried out to compare the similar stuctured BH₃ molecule. The frequency analysis was carried out using the DFT B3LYP method with a LANL2DZ basis set and the additional text being pop=full,nbo.

Summary of TlBr3 Optimisation

	Summary	TlBr3
File Type	.log File	Pentahelicene
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	LANL2DZ
Spin	Singlet
Final Energy/Hartree a.u.	-91.218
Final Gradient	0.00000009
Dipole Moment	0.00

Comparison of Vibrations

Vibration No.	Vibration Form	Frequency	Intensity	Symmetry D3H point Group and description
1		50	3.5	2 bromine atoms bend in-phase whilst the other remains stationary, all in the σh plane (E')
2		50	3.5	2 bromine atoms rock in phase whilst the other rocks out of phase all in the σh plane (E')
3		57	5.0	All 3 bromine atoms have an in-phase vibration that is perpendicular to σh plane (A2)
4		151	0	In phase symmetric stretch of all 3 bromine atoms within the σh plane (A1')
5		195	23.7	One Bromine is undergoing a asymmetric stretch with respect to the other two stretching Bromines. The Thallium moves asymmetrically to the Bromines. All the stretches are in the σh plane (E')
6		195	23.7	2 Bromine atoms have an asymmetric stretch in σh plane whilst the other remains stationary, the thallium atom rocks slightly in the σh plane as well (E')

From looking at these vibrations it can be seen fairly quickly that there are a lot of similarities with that of the BH₃ The differences are that the energies and intensities are considerably lower. This is due to the heavier atoms being involved resulting in a smaller shift from the equilibrium position and a lower change in dipole. The spectrum still shows 3 clear peaks as before due to the degeneracy of the vibrations.

Cis and Trans isomerism of Mo(CO)₄(PCl₃)₂

In this section there are two isomers of Mo(CO)₄(PCL₃)₂, cis and trans. Both the isomers were drawn out in gaussview and optimised firstly by using a LANL2Z basis set. This optimisation removed the P-Cl bonds but this is just due to gaussview representation of a bond. Gaussview has set parameters for bond lengths so will not always show the bonds of the molecule in the program. The definition of a chemical bond is given by the IUPAC gold book as followed "There is a chemical bond between two atoms or groups of atoms in the case that the forces acting between them are such as to lead to the formation of an aggregate with sufficient stability to make it convenient for the chemist to consider it as an independent 'molecular species'.

Cis initial output file http://hdl.handle.net/10042/to-7038 Trans initial output file http://hdl.handle.net/10042/to-7035

Before carrying out the second optimisation the isomers were manually adjusted. The cis complex has one of the Cl atom align cis with the CO ligand and another Cl atom in the other PCl3 ligand align trans to the same CO ligand. The trans complex was arranges such that the two PCl3 ligands were eclipsing each other in line with the axial CO axis. This conformation can be seen in the second optimisation images below. Cis secondary opt. output http://hdl.handle.net/10042/to-7040 Trans secondary opt. output http://hdl.handle.net/10042/to-7041

Summary of 1st Cis and Trans Mo complex Optimisation

	Cis Isomer	Trans Isomer	Cis	Trans
File Type	.log File	.log File	Pentahelicene	Pentahelicene
Calculation Type	FOPT	FOPT
Calculation Method	RB3LYP	RB3LYP
Basis Set	LANL2MB	LANL2MB
Spin	Singlet	Singlet
Final Energy/Hartree a.u.	-617.525	-617.5221
Final Gradient	0.00021061	0.00010364
Dipole Moment	8.4796	0.00

The tables above show differences between the cis and trans isomers. The first isomers differ very slightly making the trans the thermal product, but only just. These energy differences being so small suggests that the production of either isomer is under kinetic control. Cis frequency output file http://hdl.handle.net/10042/to-7043 Trans frequency output file http://hdl.handle.net/10042/to-7042

Summary of 2nd Cis and Trans Mo complex optimisation

	Cis Isomer	Trans Isomer
File Type	.log File	.log File	Pentahelicene	Pentahelicene
Calculation Type	FOPT	FOPT
Calculation Method	RB3LYP	RB3LYP
Basis Set	LANL2DZ	LANL2DZ
Spin	Singlet	Singlet
Final Energy/Hartree a.u.	-623.577	-623.576
Final Gradient	0.00001232	0.00000104
Dipole Moment	1.3111	0.3044

Cis Vibrations (CO)

Vibration No.	Vibration Form	Frequency	Intensity	Description
42		1945	763	The axial CO groups stretch as the equatorial stretch asymmetrically.
43		1948	1498	The axial CO groups stretch symmetrically with a small asymmetric equatorial stretch.
44		1958	632	Axial/Equatorial asymmetric stretching.
45		2023	598	Axial/Equatorial symmetric stretching.

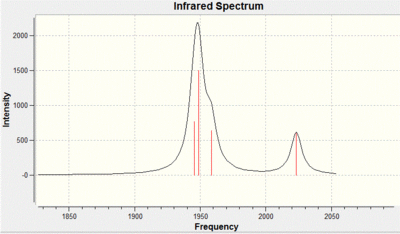
The IR spectrum shows four clear peaks CO peaks for the cis complex. This is because of the lack of symmetry in the molecule in comparison to the trans isomer. The peaks are of a high intensity due to the large change in dipole when the CO groups stretch. The dipole change is large because of the lack of symmetry in the molecule. With regards to the accuracy of the method the bond lengths can only be compared to that of [Mo(CO)4(PPh3)2] complex from literature. The mo-p bond length calculated is 2.51 angstroms whereas the literature 2.58 angstroms, The mo-c bond length calculated is 2.05 angstroms and in the literature is 2.04 angstroms. This shows that the calculation performed on gaussian is representative of the real molecule, it is a perfect comparison as the phenyl groups are a lot larger than the chlorine groups.

Trans Vibrations (CO)

Vibration No.	Vibration Form	Frequency	Intensity	Description
42		1950	1475	Asymmetric axial stretching.
43		1950	1466	Asymmetric axial/equatorial stretching.
44		1977	0.659	Symmetric stretching in the axial and equatorial planes but are in alternate phase to each other.
45		2030	3.787	In phase symmetric stretch of all axial and equatorial CO lignads

The IR spectrum shows 1 large CO peak for the trans complex. This is because of the high symmetry in the complex in comparison to the cis isomer. The degenerate peak of a high intensity is due assymmteric stretching whereas the two other peaks have high symmetry and give a small change in dipole. With regards to the accuracy of the method the bond lengths can only be compared to that of [Mo(CO)4(PPh3)2] complex from literature as before. The mo-p bond length calculated is 2.44 angstroms whereas the literature 2.36 angstroms, The mo-c bond length calculated is 2.06 angstroms and in the literature is 1.87 angstroms. As in the cis this shows that the calculation performed on gaussian is representative of the real molecule, again the comparison is not ideal.

Mini Project

D8 complexes of the transition metals have interesting properties. Depending on which four ligands are bound to the Nickel centre they can show a tetrahedral or square planar geometry. It has been shown that NiCl₄ has a square planar geometry and NiCN₄ has a teterhedral geometry.

The aim of this project is to see if the computational methods give predict the structures to be the same as that in the literature. Furthermore after an initial optimisation of the complexes a frequency analysis will be carried out to ensure the minimum energy has been obtained. Following this a molecular orbital calculation will be run using pseudo potentials.

Below are the two structures drawn to be optimised initially.

Structures to be Optimised

NiCl4	NiCN4
Pentahelicene	Pentahelicene

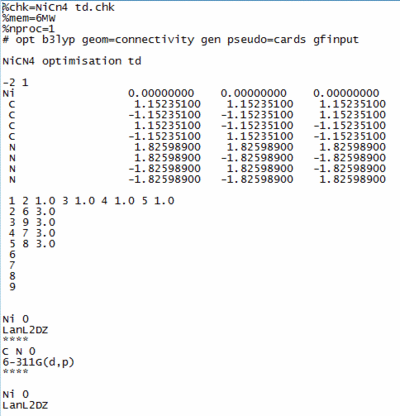
These two structures were firstly optimised using constrained point group D₄h for NiCl₄ and Td for NiCN₄. Both structures were run on gaussview as the SCAN facility had a huge que for jobs to be run. The input file below was configured in notepad so that the Nickel, Carbon and Nitrogen atoms were subject to different conditions.

The problem was that this file could not be run in the 32 steps that are inherent to gaussian calculations, in order to overcome this the values from the output of this file was copied into a new optimisation to allow what is effectively a 64 step calculation. After a long wait this file also came back with an error stating that the file had not converged. When the output file was analysed it could be seen that the problem routed in a different area. The Symmetry constraints was then removed to give the input file shown below.

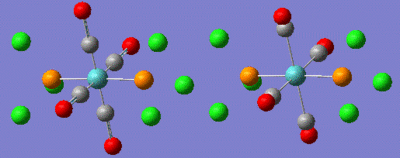
These files were then sent off to the SCAN facility to run overnight. The files had run by the following day but showed the NiCN₄ to give a non converged output whereas the NiCl₄ has converged, both shown in the image below.

The complexes below show how the results from the optimisations.

Optimised Structures

NiCl4 converged	NiCN4 non-converged
Pentahelicene	Pentahelicene

NiCl₄ Output file http://hdl.handle.net/10042/to-7045 NiCN₄ Output file http://hdl.handle.net/10042/to-7044

These optimisations although one not converged do show interesting results. The NiCN₄ complex should be tetrahedral according to the literature but with the computational calculation it would seem that it is progressing towards a square planar geometry. Although the molecule has not converged it is unlikely that it would progress back into a tetrahedral structure.

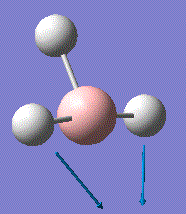
Vibrational Analysis could not be carried out (in time) on the optimised NiCl₄. However the MO's produced from the optimisation give a clue as to the reactivity of the complex.

Optimised Structures

NiCl4 HOMO	NiCl4 LUMO

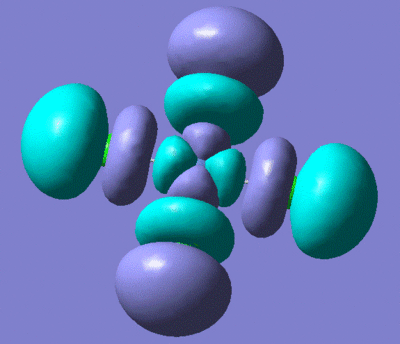
These two orbitals show that the NiCl₄ is very reactive. If the HOMO and LUMO are antibonding this would suggest that the complex would undergo ligand displacement very easily.