Rep:Mod:STrimmer1

Module 1: Structure and Spectroscopy

Samuel Trimmer

Introduction

The structure of molecules can be determined from a variety of different accruate methods, this report is focusing calculating the conformational and spectroscopic properties using computation chemsitry methods. The structure can be calculated from considering using only a classical physics model called MM2. This allows the distributions of atoms to be calculated by looking at the relative coulombic interactions. This is limited as it does not account for stereoelectronic effects, in order to become more accurate the PM6 method is used. This is a semi quantum mechanical method that not only looks at the coulombic interactions but calculates stability based on quantum mechanic principles.

These techniques are used in this module to decipher thermodynamic and kinetic products, and to give clues to the reasons behind one isomer being a more stable intermediate. Furthermore there is a mini project using these computational methods to recreate spectroscopic data and compare with that of actual analysis from literature.

Dimerisation of Cyclopentadiene and Hyrdrogenation of the Dimer

Cyclopentadiene dimerises via a Diels-Alder reaction into two possible structures, an endo dimer or an exo dimer. It is known from experimental data that the endo product is formed. In order to calculate whether the endo product is thermodynamic or kinetic the minimised energy of both the endo and exo dimers are compared using an MM2 calculation.

Dimer Comparison

Dimer Form	Energy/(kcal/mol)
Exo	31.8810
Endo	34.0111

The energy for the endo dimer is higher than the exo which means the endo structure is the kinetic product. The hydrogenation of the dimer gives two endo products indicating that the endo is not only the kinetic product but also the major product. This is explained by looking at the Diels-Alder reaction and the structures of the transition states.

The endo mechanism involves the two cyclopentadiene rings to be in a staggered confirmation. This confirmation has the dihedral angle of the two rings such that there is large torsional strain with respect to the exo prouduct. The exo product does not overlap in the same manner and has less torsional strain an hence is the lower energy product. It is thought that the major product is the endo product due to the stabilisation of the zwitterionic transition state resonance forms. It can seen in the image above that the endo product although higher in energy is stabilised by the attractive overlap in transition state.

Once the cyclopentadiene has dimerised it can undergo further reactivity at the electron rich double bonds, as there are two of them there is a possibility of two different products. Another MM2 calculation has to be carried out in order to see which one is the major product.

Hydrogenation Structures Energies

Energy Terms	Energies of Structure A/(kcal/mol)	Energies of Structure B/(kcal/mol)
Stretching	1.2761	1.1006
Bending	19.8604	14.4937
Stretch-bend	-0.8362	-0.5486
Torsion	10.8074	12.5144
Non-1,4 VDW	-1.2175	-1.0366
1,4 VDW	5.6399	4.5000
Dipole/Dipole	0.1620	0.1406
Total Energy	35.6920	31.1641

This table shows structure B to be lower in energy than A and is therefore the major product of hydrogenation. The main differences between the two structures are in the bending, torsion and 1,4 van der waal forces. This seems stability of structure to is due to the five membered ring being planar causing a rise in torsion but a decrease in the bending. Furthermore the repulsive 1,4 van der waal forces are decreased when the five membered ring is planar as the hydrogens are considerably further apart in the ring.

Stereochemistry of nucleophilic additions to a pyridinium ring (NAD+ analogue)

The two reactions shown below are both proceed with stereocontrol in the formation of their products. In order to work out how why the products have a their stereochemistry the conformation of the reactants are calculated. Looking firstly at the prolinol derivative it would seem that the lowest energy conformation has the carbonyl on one face of the molecule and the five membered ring bent in the direction of the opposite face. The mechanism involves the magnesium of the grignard reagent coordinating to the carbonyl and results in the methyl substituting onto that face, Structure A is the reactant pictured below.

The second reaction is that of a pyridinium ion with aniline. I placed the atoms in a lower energy confirmation,from my understanding of the sterics, and then using the molecular dynamics calculations in chembio to get the minimised energy for the molecule. This showed that the large R group attached to the nitrogen of the 7 membered ring is on one face of the molecule and is locked in this confirmation. The alanine does not coordinate to the oxygen but is forced onto the other face in the reaction to avoid steric clash of the phenyl groups and the R groups of the reactant, Structure B is the reactant pictured below.

Additions to Pyridinium Ring

Energy Terms	Energies of Reactant A/(kcal/mol)	Energies of Reactant B/(kcal/mol)	Structure A	Structure B
Stretching	2.0653	3.9748	Pentahelicene	Pentahelicene
Bending	14.1324	11.6774
Stretch-bend	0.1663	0.4017
Torsion	6.3456	9.5299
Non-1,4 VDW	-0.6682	3.4550
1,4 VDW	16.7007	29.3948
Charge Dipole	9.8133	9.0819
Dipole/Dipole	-3.9278	-4.8943
Total Energy	44.6281	62.6212

The reaction calculation could be improved by accounting for the kinetics. Only considering the thermodynamics for this situation does not account for how a nucleophile would attack, in an actual reactions there are many other parameters effecting the way a molecule will react other than just its confirmation.

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

The synthesis of taxol involves two key intermediate which are isomers of each other in which a carbonyl is on opposite faces. The isomers are examples of atropisomerism which is the formation of two different isomers due to the steric hinderancein the molecule, in this case forcing the carbonyl group to be either up or down in the molecule. It would seem from carrying out the MM2 on the two isomers that isomer 10 has the lowest energy conformation. When carrying out the MMFF92 this is also the case except there is a larger difference in the energy of the two.

Tazol Reaction Energies

Energy Terms	Energies of Reactant 9/(kcal/mol)	Energies of Reactant 10/(kcal/mol)	Structure 9	Structure 10
Stretching	2.0653	3.9748	Pentahelicene	Pentahelicene
Stretch	3.0584	2.6439
Bending	20.5178	11.2777
Stretch-bend	0.5230	0.3559
Torsion	22.1051	23.0625
Non-1,4 VDW	-0.7376	-1.1582
1,4 VDW	14.2415	13.9857
Dipole/Dipole	-0.0215	-0.1816
Total Energy	59.7297	49.9857

The reaction is slowed down due to the hyperstability of bridgedhead alkenes, they are extremely unreactive ever more so with the bulky methyl groups on the bridge. This causes the reaction to be particularly slow because of this large stability. When Removing the double bond from both structures there is a clear increase over energy structure 9 goes up to 69.8 kcal/mol and structure 10 up 55 kcal/mol. These hyperstable alkenes are related to bret's rule which states:

In polycyclic systems having atomic bridges, the existence of a compound having a carbon-carbon or carbon-nitrogen double bond at a bridgehead position is not possible, except when the rings are large, because of the strain which would be introduced in its formation by the distortion of bond angles and/or distances. As a corollary, reactions which should lead to such compounds will be hindered or will give products having other structures.

The reason that the structure is so stable is from a cage like structure formed by the alkene bond with the bridge, the difference between the two energies, with and without the cage like structure, is known as the olefin stabilization energy.

Modelling Using Semi-empirical Molecular Orbital Theroy

The MM2 calculation used previously is now not always the best way to decipher reactivity. This section considers secondary orbital overlap using MM2 to gain the structure and a MOPAC/PM6 method to obtain molecular orbitals. The molecules being focused are the dichlorcarbene Molecule A, and the anti hydrogenated molecule B.

Dichlorocarbene contains two double bonds which are susceptible to electrophilic attack. In order to decide which one of the double bonds is more susceptible to attack the conformation will be calculated using the MM2 and then the molecular orbitals calculated using the MOPAC interface, The images of the orbitals are shown below.

Molecular Orbitals for Dichlrocarbene

HOMO-1	HOMO

LUMO	LUMO+1	LUMO+2

When you observe the HOMO-1 it is clear that there is secondary orbital overlap between that of the chlorine atom and the double bonds orbital in a constructive manner as both orbitals are in the same phase. This overlap results in the chlorine atom withdrawing electron density from the double bond. This will decrease the double bond below the chlorine reactivity to electrophilic attack meaning that the other double bond going to be attacked.

The effect of the C-Cl bond can be viewed by calculating the vibrational frequency of two different molecules, one containing both double bonds, molecule A, and one with just the one double bond, the anti double bond has been hydrogenated molecule B. The orbitals for molecule A were pictured above and those for B are pictured below.

Molecular Orbitals for the monoalkene

HOMO-1	HOMO

LUMO	LUMO+1	LUMO+2

From studying the orbitals and the vibrational frequencies of the C-CL and C=C bonds it would seem that the syn bond is indeed stronger than the anti bond in the dichlorocarbene molecule A, which confirms the idea of the secondary orbital overlap stabilising the bond. Furthermore the C-Cl bond is weaker in the dichlorocarbene molecule A with respect to molecule B. This may be because the secondary orbital overlap is causing the bond to become more polarised and therefore not as stable. The molecular orbitals seem to show that there is no secondary orbital overlap in the molecule B which follows with the vibration data however the data may not be accurate as the calculations are not gospel. Also the rigidity of a molecule is changed when a double bond is removed meaning that a comparison of the vibrational data is not completely accurate.

Comparison of Vibrations

Molecule	C=C Stretch (cm-1)	C-Cl Stretch/(cm-1)
A	1757.4 (syn) 1737.1 (anti)	770.9
B	1758.2	775.0

Mini Project Research

This project is using computational chemistry to analyse an already reported literature reaction. This will test the accuracy and ability of the computational methods and also the question the accuracy of the spectroscopic data reported.

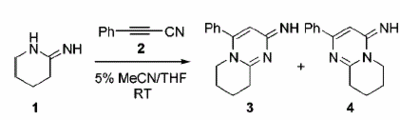
In order to carry out this task I searched the jacs database for a reaction that forms regioisomers that have carbon NMR peaks that differ by more than 5ppm, to avoid the inherent error of the computational method. The reaction found is the "Selective Formation of Iminopyrimidine Regioisomers"pictured below.

The carbon NMR of both isomers was run using gaussian and sent to SCAN to do the calculations, the results are tabulated below.

Isomer 3 Carbon NMR

Isomer 3 Carbon NMR shifts

Carbon Atom Label	Isomer 3 Carbon NMR calculated/(ppm)	Isomer 3 Carbon NMR Lit./(ppm)	Isomer 3
3	22.4	18.1
2	25.1	21.8
4	33.4	31.3
1	49.1	50.3
9	111.1	106.6
13	124.2	128.3
14	125.0	129.5
12	125.0	129.5
15	125.2	129.5
16	125.9	130.6
11	132.7	131.5
10	144.3	157.4
5	148.9	163.2
8	151.0	163.5

Isomer 4 Carbon NMR

Isomer 4 Carbon NMR shifts

Carbon Atom Label	Isomer 4 Carbon NMR calculated/(ppm)	Isomer 4 Carbon NMR lit./(ppm)	Isomer 4
3	20.7	18.1
4	23.4	21.4
2	33.6	33.3
5	45.0	47.0
8	105.0	101.4
17	122.0	122.0
13	123.0	123.0
16	124.0	127.5
14	124.5	129.1
15	125.0	129.1
11	132.7	132.2
9	149.0	157.7
7	149.6	158.3
1	153.0	161.2

The computed NMR for Isomer 3 and Isomer 4 has shown that using computational methods you can distinguish between the two isomers in the same manner as in the literature. When reading through the tables it can be seen that the general trend of the two isomers matches that of the literature. The computational calculation of the carbon NMR has not calculated the exact same values for the NMR in the literature but this is due to the inherent error in the calculation. The important relative shifts between the calculated NMR for each isomer and the relative shifts for the literature NMR. From the tables it can be seen and is most obvious for carbon 9 in isomer 3 and carbon 8 in isomer 4 (different labelling of the same carbon due to gaussview). In literature these two peaks are the 5.2ppm different and in the computational calculation are 6.1 ppm different. It would seem that the difference is due to the phenyl group attached being at a different orientation for each isomer, Isomer 4 is linear where as the phenyl group is angled out of the plane.

The results of this NMR are not conclusive due to the error in the computational method and the literature does not seem to report accurately. When calculated computationally all 14 carbons give a different shift whereas in the literature the actual NMR cannot always distinguish between peaks that are very close in value.

As well as the NMR the IR was computed in order to see if there the Isomers could be distinguishable, the literature did not report any IR values. Below are the two computed IR spectrums for Isomer 3 and 4.

IR Spectrum Isomer 3

IR Spectrum Isomer 4

The two IR spectra share one main peak at 1747 wavenumbers, this vibration is that of the central ring and the nitrogen double bond. The vibration that is different is the 1660 vibration in both molecules, one is substatially lower than the other. This vibration is that of the nitrogen double bond and the phenyl group attached. This is larger in isomer 4 maybe due to the phenyl ring being in the same plane as the central nitrogen ring. Another differing vibration is that at 1484 wavenumbers which is present in isomer 3 but not in 4. In the vibration the 5 membered ring and central ring vibrate in the same plane, this vibration may not occur in isomer 4 due to the rigidity of the structure and the steric clash of the 5 membered ring with the nitrogen double bond.

Overall it would seem that the IR would be a better method to distinguish between the two molecules as there is a more distinct difference between the two isomers. That is not to say that the Carbon NMR is not sufficient it is just not quite as clear a contrast between the isomers.