Rep:Mod:SSYL Computational Labs - Module 3
Selina Leung
Introduction
This project investigates the transition states for the Cope rearrangement of 1,5-hexadiene and two Diels-Alder reactions (ethylene with cis-butadiene and maleic anhydride with cyclohexa-1,3-diene). Gaussian was used for the calculations.
PART 1: The Cope Rearrangement
The Cope rearrangement involves a [3,3]-sigmatropic rearrangement of 1,5-dienes under heated conditions. The transition state of the rearrangment involves the movement of 4n+2 electrons (6 electrons in total for 1,5-Hexadiene). This project aims to deduce the mechanism of the rearrangment by analysing the transition state of the reaction which can exist in either the "boat" conformation or the "chair" conformation. The reaction scheme is shown below:
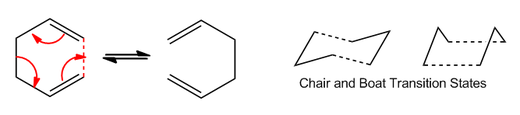
It has been suggested that the rearrangement are concerted where the reaction proceeds without formation of an intermediate. But also in addition, the bonds are formed and broken simulataneously. From the energies of the transition states tabulated below, it can be seen that the chair and boat conformations have different energies where the chair transition state possesses a lower energy that the boat.
| Transition State | ΔE (kcalmol-1) | CASSCF Energies relative to trans 1,5-hexadiene at 523 K.[1] |
| Chair | 40.7 | |
| Boat | 47.3 |
A molecule of 1,5-hexadiene was first analysed using GaussView, followed by the two transition state structures which were then compared.
Comparison of 1,5-Hexadiene Conformations
A molecule of hexadiene was produced in GaussView and optimised using the Hartree-Fock 3-21G Basis Set. This was repeated to give the different conformations, shown in the table below. Each conformation has been tabulated with its point group, bond geometries and energies. Out of the four conformations computed, the gauche 3 conformation appears to have the lowest energy and gauche 2 the highest. However, other conformers exist that have not been computed. It would be expected that the Anti conformations would have the lowest energy due to less sterical strain in the arrangment of the atoms, compared to the Gauche conformations.
| Structure | Energy (au) | Point Group | Bond Lengths (Å) | Dihedral Angle (°) | Log File |
 |
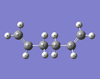-231.69260235 | C2 | C-C: 1.55230 C-C: 1.50888 C=C: 1.31610 |
-176.899 | Download |
 |
-231.69253528 | Ci | C-C: 1.55275 C-C: 1.50891 C=C: 1.31613 |
180.000 | Download |
 |
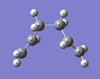-231.69166702 | C2 | C-C: 1.55082 C-C: 1.50831 C=C: 1.31566 |
-64.713 | Download |
 |
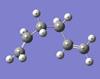-231.69266122 | C1 | C-C: 1.55329 C-C: 1.508923 C=C: 1.31647 |
-67.706 | Download |
The dihedral angles for the two Gauche conformations show that the bonds around the central C-C atoms are bent in closer together. However, the two Anti conformations both have dihedral angles of effectively 180° (and so an antiperiplaner arrangement). Antiperiplanar arrangements are typically the lowest in energy, again due to sterics where repulsion between the bulkier groups are minimised.
Optimisation of Anti 2 1,5-Hexadiene using a 6-31G(d) Basis Set
The "Anti 2" conformation was taken and further optimised using the DFT B3LYP 6-31G(d) method and basis set. The results are shown below and results compared with the originally optimised 3-21G molecule.
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d) |
| Charge | 0 |
| Spin | Singlet |
| Energy (au) | -234.61170194 |
| RMS Gradient Norm (au) | 0.00001319 |
| Dipole Moment (D) | 0.0000 |
| Point Group | Ci |
There appears to be no significant change in geometry between the two opimisation levels, however, there is a change in energy of -2.91916666 au (7664.27 kJmol-1) due to the accuracy of the basis sets. This is quite a large energy difference.
| Bond |
HF 3-21G Length (Å) |
DFT 6-31G(d) Length (Å) |
 |
| C1-C2 | 1.55275 | 1.54810 | |
| C2-C7 | 1.50891 | 1.50423 | |
| C1-C12 | 1.50891 | 1.50423 | |
| C12=C13 | 1.31613 | 1.33350 | |
| C7=C8 | 1.31613 | 1.33350 |
Item Value Threshold Converged? Maximum Force 0.000016 0.000450 YES RMS Force 0.000006 0.000300 YES Maximum Displacement 0.000198 0.001800 YES RMS Displacement 0.000081 0.001200 YES Predicted change in Energy=-1.629719D-08 Optimization completed. -- Stationary point found.
Frequency Analysis of Anti 2 1,5-Hexadiene
Frequency analysis was carried out on the reoptimised Anti 2 1,5-hexadiene molecule by changing the job method to "Frequency". The output file was checked to ensure that the first line of low frequencies are low and the second line shows no negative frequencies. This ensures that the molecule is at a minimum.
Low frequencies --- -29.5969 -11.3355 -0.0002 0.0008 0.0008 6.3672 Low frequencies --- 72.9020 80.5854 120.0804
The predicted IR spectrum for Anti 2 1,5-hexadiene was obtained from the results along with its vibrational data.
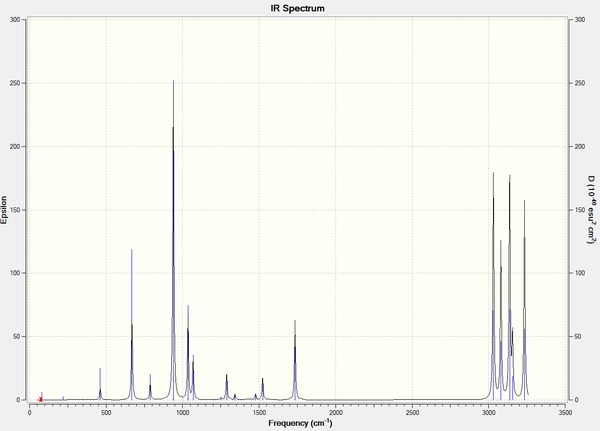
Below is the list of vibrational modes for the molecule. A total of 42 modes was found, many of which have intensities of 0. This is because they involve no shift in the position of the dipole moment, thus do no interact with the electromagnetic field. This is why less peaks are observed in the predicted IR spectrum (seen above) than listed below.
| Vibration | Frequency | Intensity | Vibration | Frequency | Intensity | |
| 1 | 72.90 | 0.0170 | 22 | 1287.90 | 6.5479 | |
| 2 | 80.59 | 0.1177 | 23 | 1322.83 | 0.0000 | |
| 3 | 120.08 | 0.0000 | 24 | 1338.33 | 0.0000 | |
| 4 | 218.85 | 0.1525 | 25 | 1342.60 | 1.3820 | |
| 5 | 348.54 | 0.0000 | 26 | 1383.88 | 0.0000 | |
| 6 | 394.99 | 0.0000 | 27 | 1474.26 | 0.0000 | |
| 7 | 461.97 | 2.9062 | 28 | 1476.78 | 1.5139 | |
| 8 | 625.44 | 0.0000 | 29 | 1508.67 | 0.0000 | |
| 9 | 669.09 | 19.9099 | 30 | 1522.82 | 5.6151 | |
| 10 | 788.36 | 4.0163 | 31 | 1731.37 | 0.0000 | |
| 11 | 938.14 | 0.0000 | 32 | 1734.63 | 18.1371 | |
| 12 | 938.59 | 14.7113 | 33 | 3021.30 | 0.0000 | |
| 13 | 939.66 | 59.3995 | 34 | 3030.82 | 53.5537 | |
| 14 | 941.94 | 0.0000 | 35 | 3059.73 | 0.0000 | |
| 15 | 1002.63 | 0.0000 | 36 | 3079.73 | 35.8657 | |
| 16 | 1033.32 | 0.0000 | 37 | 3135.82 | 0.0000 | |
| 17 | 1035.56 | 19.3742 | 38 | 3136.91 | 55.9329 | |
| 18 | 1042.53 | 0.0000 | 39 | 3155.87 | 14.8859 | |
| 19 | 1068.47 | 9.5456 | 40 | 3156.13 | 0.0000 | |
| 20 | 1203.16 | 0.0000 | 41 | 3234.08 | 0.0000 | |
| 21 | 1250.48 | 0.5751 | 42 | 3134.11 | 45.4609 |
Below are a selection of the vibrations with particularly strong intensities.
 |
 |
 |
 |
 |
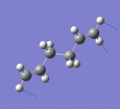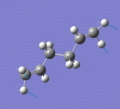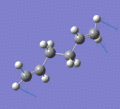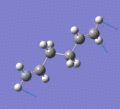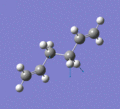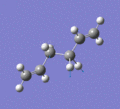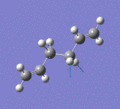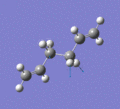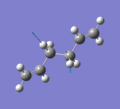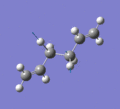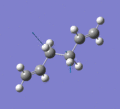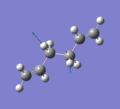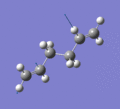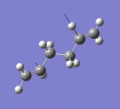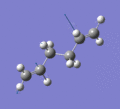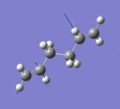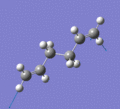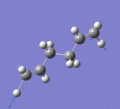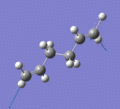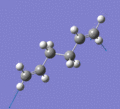From the output file, the following data was also obtained:
| Energy (au) | |
| Sum of electronic and zero-point Energies | -234.469217 |
| Sum of electronic and thermal Energies | -234.461861 |
| Sum of electronic and thermal Enthalpies | -234.460917 |
| Sum of electronic and thermal Free Energies | -234.500821 |
Confirmation of Optimisation
After each optimisation calculation, the output file was checked in order to see if the molecule had fully converged.
Anti 1
Item Value Threshold Converged? Maximum Force 0.000056 0.000450 YES RMS Force 0.000010 0.000300 YES Maximum Displacement 0.001274 0.001800 YES RMS Displacement 0.000459 0.001200 YES Predicted change in Energy=-2.090780D-08 Optimization completed. -- Stationary point found.
Anti 2
Item Value Threshold Converged? Maximum Force 0.000060 0.000450 YES RMS Force 0.000010 0.000300 YES Maximum Displacement 0.000376 0.001800 YES RMS Displacement 0.000171 0.001200 YES Predicted change in Energy=-2.037007D-08 Optimization completed. -- Stationary point found.
Gauche 2
Item Value Threshold Converged? Maximum Force 0.000008 0.000450 YES RMS Force 0.000003 0.000300 YES Maximum Displacement 0.000206 0.001800 YES RMS Displacement 0.000055 0.001200 YES Predicted change in Energy=-2.478210D-09 Optimization completed. -- Stationary point found.
Gauche 3
Item Value Threshold Converged? Maximum Force 0.000011 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.001095 0.001800 YES RMS Displacement 0.000297 0.001200 YES Predicted change in Energy=-8.759526D-09 Optimization completed. -- Stationary point found.
Optimising the "Chair" and "Boat" Configurations
An allyl CH2CHCH2 was first optimised using the Hartee-Fock 3-21G basis set to give the planar fragment below. This will be used to form the chair and boat transition states later on.
| File Type | .log |  |
| Calculation Type | FOPT | |
| Calculation Method | UHF | |
| Basis Set | 3-21G | |
| Charge | 0 | |
| Spin | Doublet | |
| Energy (au) | -115.82304011 | |
| RMS Gradient Norm (au) | 0.00000297 | |
| Dipole Moment (D) | 0.0292 | |
| Point Group | C2v |
Item Value Threshold Converged? Maximum Force 0.000006 0.000450 YES RMS Force 0.000003 0.000300 YES Maximum Displacement 0.000176 0.001800 YES RMS Displacement 0.000060 0.001200 YES Predicted change in Energy=-8.765549D-10 Optimization completed. -- Stationary point found.
Optimisation of the Chair Transition State
A) Optimisation of Transition State
The allyl fragment from the previous step was then duplicated and arranged into a chair transition state, ensuring that the distance between the terminal ends of the allyl fragments were around 2.2 Å (this was carried out by manually setting the bond lengths). The new structure was reoptimised using the "Opt+Freq" method, with the optimisation setting changed to "TS (Berny)" and the force constants to be calculated once. The additional keywords opt=noeigen was also added. The summary of results is shown below along with the point group once the molecule had been symmetrized in GaussView.
| Terminal C-C Distance | 2.02057 Å |  |
| C-C Bond Length | 1.38924 Å | |
| C-C-C Bond Angle | 120.499° | |
| File Type | .log | |
| Calculation Type | FREQ | |
| Calculation Method | RHF | |
| Basis Set | 3-21G | |
| Charge | 0 | |
| Spin | Singlet | |
| Energy (au) | -231.61932240 | |
| RMS Gradient Norm (au) | 0.00002345 | |
| Dipole Moment (D) | 0.0001 | |
| Point Group | Ci |
An imaginary frequency was also found at -817.88 cm-1. This vibrational mode is shown below which shows the reaction pathway as the terminal C-C bonds on one end approach each other to form one C-C σ-bond.
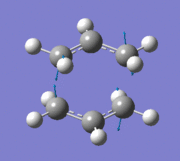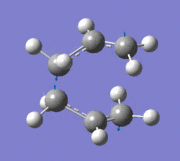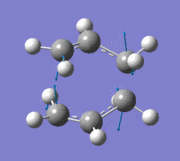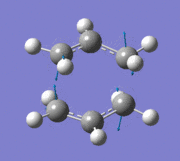
Item Value Threshold Converged? Maximum Force 0.000055 0.000450 YES RMS Force 0.000013 0.000300 YES Maximum Displacement 0.000961 0.001800 YES RMS Displacement 0.000181 0.001200 YES Predicted change in Energy=-7.303118D-08 Optimization completed. -- Stationary point found.
Low frequencies --- -817.8849 -2.4395 -0.0007 -0.0007 -0.0003 2.8347 Low frequencies --- 4.8020 209.5700 395.8888
B) Optimisation using the Frozen Coordinate Method
A separate optimisation of the chair transition state was carried out. This was done by creating a guess structure for the transition state as before, and once again setting the terminal bond distances manually to 2.20 Å. The terminal carbon atoms were then set as frozen coordinates (in order to maintain the bond length) using the Redundant Coordinate Editor. An optimisation calculation was then run as a minimum. The structure produced is very similar to the previous.
| Terminal C-C Distance | 2.20 Å |  |
| C-C Bond Length | 1.38127 Å | |
| C-C-C Bond Angle | 121.967° | |
| File Type | .log | |
| Calculation Type | FOPT | |
| Calculation Method | RHF | |
| Basis Set | 3-21G | |
| Charge | 0 | |
| Spin | Singlet | |
| Energy (au) | -231.61518525 | |
| RMS Gradient Norm (au) | 0.00325802 | |
| Dipole Moment (D) | 0.0004 | |
| Point Group | C2h |
Item Value Threshold Converged? Maximum Force 0.000014 0.000450 YES RMS Force 0.000003 0.000300 YES Maximum Displacement 0.001069 0.001800 YES RMS Displacement 0.000221 0.001200 YES Predicted change in Energy=-1.726556D-08 Optimization completed. -- Stationary point found.
C) Optimisation of the Terminal Bonds
The molecule optimised in the previous step using the frozen coordinate method was further optimised, however, this time using the Redundant Coordinate Editor to set the terminal bonds as "Derviative" rather than "Freeze Coordinate" as before. The structure was optimised as a transition state.
| Terminal C-C Distance | 2.01989 Å |  |
| C-C Bond Length | 1.38933 Å | |
| C-C-C Bond Angle | 120.508° | |
| File Type | .log | |
| Calculation Type | FTS | |
| Calculation Method | RHF | |
| Basis Set | 3-21G | |
| Charge | 0 | |
| Spin | Singlet | |
| Energy (au) | -231.61932200 | |
| RMS Gradient Norm (au) | 0.00005486 | |
| Dipole Moment (D) | 0.0002 | |
| Point Group | C2h |
The bond lengths calculated are very similar to the bonds calculated in Part (A).
Item Value Threshold Converged? Maximum Force 0.000027 0.000450 YES RMS Force 0.000008 0.000300 YES Maximum Displacement 0.000957 0.001800 YES RMS Displacement 0.000180 0.001200 YES Predicted change in Energy=-2.942683D-07 Optimization completed. -- Stationary point found.
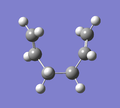
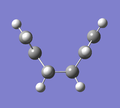
D) Intrinsic Reaction Coordinate (IRC)
For the optimised transition state using the frozen coordinate method, a new calculation was set up using the job type "IRC". "Follow IRC" was set to "Forward Only" and the steps was set to 50. The calculation had completed after 44 steps. A selection of the results are shown below alongside the step number. It can be seen that the fragments approach each other at one end (Steps 1 to 10) and form a C-C bond (Step 11). The ends of the molecules then distorts to what appears to be more like the Gauche 2 conformation (Step 44), rather than the Anti 2 conformation that was started with.
 |
 |
 |
 |
 |
 |
 |
 |
 |
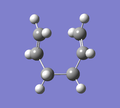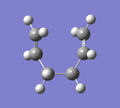Optimisation of the Boat Transition State
A) Optimisation using the QST2 Method
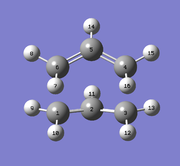
The optimised Anti 2 1,5-Hexadiene molecule from Part 1 was used for this calculation. A reactant and product molecule of the hexadiene was created in the same molecule window, and the carbon atoms numbered as shown below. The dihedral angle of the central 4 atoms was set to 0° and the C-C-C bond angles of the central 4 carbons set as 100°.
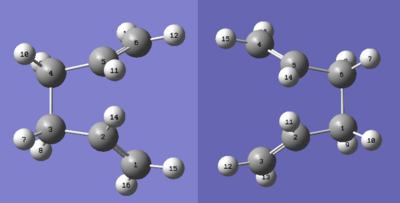
The job type was set as "Opt+Freq" and optimised using the TS (QST2) setting. The structure of the boat transition state is shown below:
| Terminal C-C Distance | 2.01989 Å |  |
| C-C Bond Length | 1.38933 Å | |
| C-C-C Bond Angle | 120.508° | |
| File Type | .log | |
| Calculation Type | FREQ | |
| Calculation Method | RHF | |
| Basis Set | 3-21G | |
| Charge | 0 | |
| Spin | Singlet | |
| Energy (au) | -231.60280241 | |
| RMS Gradient Norm (au) | 0.00002428 | |
| Dipole Moment (D) | 0.1582 | |
| Point Group | C2v |
Item Value Threshold Converged? Maximum Force 0.000099 0.000450 YES RMS Force 0.000017 0.000300 YES Maximum Displacement 0.001761 0.001800 YES RMS Displacement 0.000420 0.001200 YES Predicted change in Energy=-8.060687D-08 Optimization completed. -- Stationary point found.
Activation Energies: Optimisation of the Transition States using B3LYP/6-31G(d)
The HF/3-21G optimised chair and QST2 boat TS structures cab be further optimised using the B3LYP/6-31G(d) method and basis set. The activation energy can then be calculated from the energies obtained from each of the transition states.
A) Optimisation of the Chair TS
The previously optimised HF/3-21G was used for this calculation. The job type was set to "Optimisation" and instead of Hartree-Fock, "DFT" was selected with the B3LYP method and 6-31G d basis set. It can be seen that the bond lengths have shortened and the terminal C-C distance has also reduced compared to the previous optimisation. There is also a large energy difference of -2.93766127 au.
| Terminal C-C Distance | 1.96710 Å |  |
| C-C Bond Length | 1.40753 Å | |
| C-C-C Bond Angle | 119.946° | |
| File Type | .log | |
| Calculation Type | FTS | |
| Calculation Method | RB3LYP | |
| Basis Set | 6-31G(d) | |
| Charge | 0 | |
| Spin | Singlet | |
| Energy (au) | -234.55698367 | |
| RMS Gradient Norm (au) | 0.00001249 | |
| Dipole Moment (D) | 0.0000 | |
| Point Group | Ci |
Item Value Threshold Converged? Maximum Force 0.000027 0.000450 YES RMS Force 0.000005 0.000300 YES Maximum Displacement 0.000110 0.001800 YES RMS Displacement 0.000036 0.001200 YES Predicted change in Energy=-4.974933D-09 Optimization completed. -- Stationary point found.
B) Optimisation of the Boat TS
The boat TS optimised using the QST2 method in the previous section was used for this calculation. Again, there is some deviation of the geometry of the molecule with the previously optimised one. There is also an energy difference of 2.94029063 au (a large difference as expected).
| Terminal C-C Distance | 2.20615 Å |  |
| C-C Bond Length | 1.39325 Å | |
| C-C-C Bond Angle | 122.268° | |
| File Type | .log | |
| Calculation Type | FTS | |
| Calculation Method | RB3LYP | |
| Basis Set | 6-31G(d) | |
| Charge | 0 | |
| Spin | Singlet | |
| Energy (au) | -234.54309304 | |
| RMS Gradient Norm (au) | 0.00000871 | |
| Dipole Moment (D) | 0.0614 | |
| Point Group | C2v |
Item Value Threshold Converged? Maximum Force 0.000017 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000768 0.001800 YES RMS Displacement 0.000200 0.001200 YES Predicted change in Energy=-3.621263D-08 Optimization completed. -- Stationary point found.
Activation Energies for the Chair and Boat Transition States
The data obtained from the HF/3-21G optimsations are tabulated below and the activation energies calculated using the energy from the B3LYP/6-31G(d) optimised Anti 2 conformer is tabulated below. The activation energy was calculated by taking energy difference between each of the transition states and the Anti 2 conformer. The values were converted from hartree au to kJmol-1 and kcalmol-1 for a better comparison.
| Transition State | HF/3-21G Energy (au) | B3LYP/6-31G Energy (au) | ΔE Activation Energy (kJmol-1) | (kcalmol-1) |
| Anti 2 Molecule | -231.69253528 | -234.61170194 | ||
| Chair | -231.61932240 | -234.55698367 | 143.66 | 34.34 |
| Boat | -231.60280241 | -234.54309304 | 180.13 | 43.05 |
(1 hartree au = 2625.50 kJmol-1 = 627.51 kcalmol-1)[2]
As established earlier, it can be seen that there is a great difference in energy between the 3-21G and 6-31G(d) optimised molecules due to the different basis sets used. The chair transition state appears to have a lower activation energy than that of the boat transition state. This may be because the chair could be less sterically hindered (as the fragments are arranged rotated opposite each other) than the boat (where the fragments are adjacent and face the same way). Therefore, there could be less steric clash between the hydrogen atoms in the chair conformation.
The IRC analysis carried out previously seemed to show the chair transition state forming a Gauche 2 conformation, rather than the Anti 2 conformation. The HF/3-21G optimised Gauche 2 conformation has an energy of -231.69166702 au, thus differs from the Anti 2 energy (-231.69253528). Hence, there may be some degree of error upon the calculation of the activation energy. Even so, the activation energy for the chair should still be lower than for the boat transition state.
PART 2: Diels-Alder Cycloaddition
Diels-Alder cycloaddition occurs between a conjugated diene and an alkene, involving 4n+2 electrons. This section investigates two Diels-Alder reactions: ethylene with cis-butadiene and maleic anhydride with cyclohexa-1,3-diene. The HOMOs and LUMOs of each transition state structure will be computed. The significance of the HOMO and LUMO symmetries is because orbitals can only overlap if they have similar symmetry properties. If they differ in symmetry, overlap is not possible and thus the reaction does not occur.
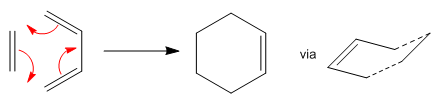
A) cis-Butadiene
A molecule of cis-butadiene was first optimised using HF/3-21G (Log File), followed by further optimisation using the B3LYP/6-31G(d) method and basis set (Log File). The summary of results after the second optimisation is shown below:
| C=C Bond Length | 1.33985 Å |  |
| C-C Bond Length | 1.47144 Å | |
| C-C-C Bond Angle | 127.279° | |
| File Type | .log | |
| Calculation Type | FOPT | |
| Calculation Method | RB3LYP | |
| Basis Set | 6-31G(d) | |
| Charge | 0 | |
| Spin | Singlet | |
| Energy (au) | -155.98594960 | |
| RMS Gradient Norm (au) | 0.00003232 | |
| Dipole Moment (D) | 0.0852 | |
| Point Group | C2v |
Item Value Threshold Converged? Maximum Force 0.000073 0.000450 YES RMS Force 0.000024 0.000300 YES Maximum Displacement 0.000294 0.001800 YES RMS Displacement 0.000140 0.001200 YES Predicted change in Energy=-2.787231D-08 Optimization completed. -- Stationary point found.
The HOMO and LUMO of cis-butadiene was also obtained. The HOMO is expected to be antisymmetric, and the LUMO symmetric. From the calculations, the HOMO was indeed found to be antisymmetrical with a nodal plane whereas the LUMO is symmetrical around a plane though the center.
 |
 |
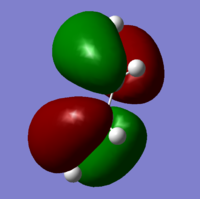B) cis-Butadiene and Ethylene Transition State
A guess structure of the transition state was produced in GaussView and the terminal carbon distances set to 2.20 Å and their coordinates frozen. The structure was then optimised to a minimum using the AM1 semi-empirical molecular orbital method.
| File Type | .log |  |
| Calculation Type | FOPT | |
| Calculation Method | RAM1 | |
| Basis Set | ZDO | |
| Charge | 0 | |
| Spin | Singlet | |
| Energy (au) | 0.10745363 | |
| RMS Gradient Norm (au) | 0.00619342 | |
| Dipole Moment (D) | 0.4149 | |
| Point Group | Cs |
Item Value Threshold Converged? Maximum Force 0.000062 0.000450 YES RMS Force 0.000019 0.000300 YES Maximum Displacement 0.000893 0.001800 YES RMS Displacement 0.000269 0.001200 YES Predicted change in Energy=-6.379689D-08 Optimization completed. -- Stationary point found.
Optimisation: Download Log File
The TS optimisation was then completed by unfreezing the terminal bonds (set to "Derivative") and also using the AM1 semi-empirical method and basis set. The terminal bond length was optimised as 2.11927 Å.
| File Type | .log |  |
| Calculation Type | FTS | |
| Calculation Method | RAM1 | |
| Basis Set | ZDO | |
| Charge | 0 | |
| Spin | Singlet | |
| Energy (au) | 0.11165477 | |
| RMS Gradient Norm (au) | 0.000003825 | |
| Dipole Moment (D) | 0.5606 | |
| Point Group | Cs |
Item Value Threshold Converged? Maximum Force 0.000091 0.000450 YES RMS Force 0.000013 0.000300 YES Maximum Displacement 0.001292 0.001800 YES RMS Displacement 0.000202 0.001200 YES Predicted change in Energy=-1.068318D-07 Optimization completed. -- Stationary point found.
Optimisation: Download Log File
The HOMO and LUMO were also obtained for the transition state. The HOMO is antisymmetrical whereas the LUMO has a plane of symmetry though the C=C bond. Again, there is a nodal plane in the HOMO.
 |
 |
|
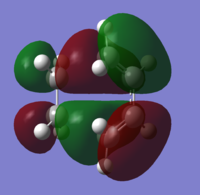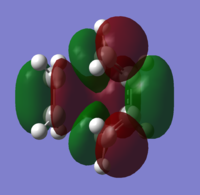Frequency analysis was then also carried out to see if there were any imaginary frequencies (similar to the chair transition state for the Cope rearrangment in the previous section). There appeared to be an imaginary frequency at -956.0808 cm-1.
Low frequencies --- -956.0808 -5.5823 -2.1447 -0.8758 -0.0032 0.0310 Low frequencies --- 0.0716 147.0674 246.7503
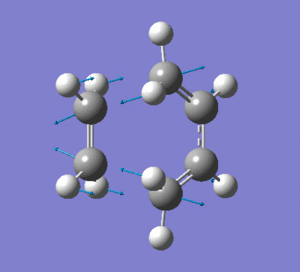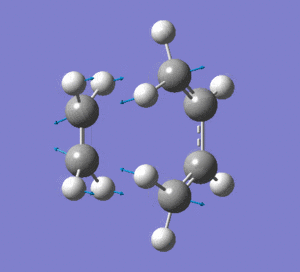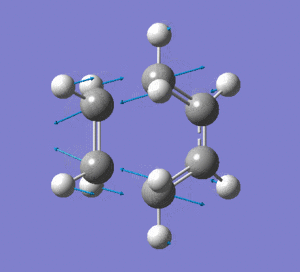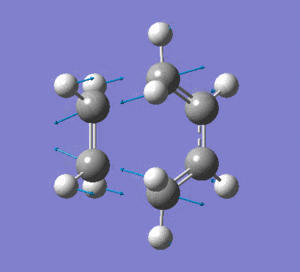
This vibration shows the transition state in the process of forming the two new C-C σ-bonds. It can be seen that the terminal carbon atoms from each fragment approach each other simultaneously and therefore the σ-bonds must be formed at the same time (synchronous). The vibration corresponds to the reaction pathway. The lowest positive frequency is at 147.0674 cm-1.. It does not show any interaction between the ethylene and butadiene fragments that would correspond to any bond formation. Each fragment appears to show asymmetrical movement that are likely to be independent of one another.
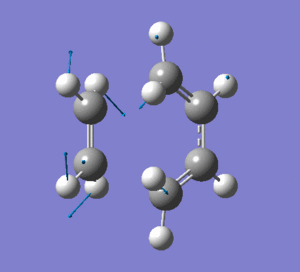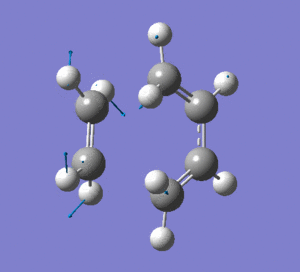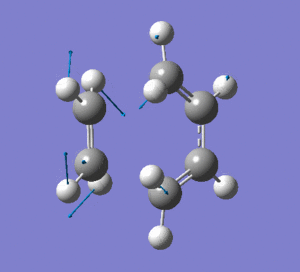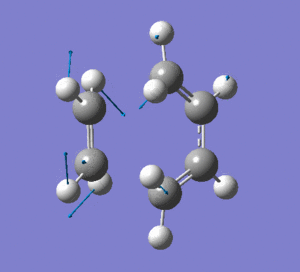
Frequency Analysis: Download Log File
Analysis and Discussion
The C-C bonds already present in the structure are all around 1.38 to 1.40 Å. Typical C-C bond lengths of an alkane is around 1.54 Å. For a C=C bond of an alkene, the bond length is around 1.42 Å [3] The van der Waals radius of a carbon atom is 1.70 Å [4]
For the ethylene/cis-butadiene transition state, the C-C terminal bond lengths were found to be 2.11927 Å, which is significantly larger than typical C-C bonds. This is also much larger than the van der Waals radius of a carbon atom. However, the terminal carbon atoms are within the range to interact as it is within twice the van der Waals radius (3.4 Å) as two atoms are involved. This indicates that these σ-bonds of the transition states have not fully formed and so the C-C distance is much greater than the bond lengths from lierature. However, there must be some degree of bonding interaction present between the terminal carbon atoms.
The reaction involves the interaction between the π/ π* orbitals of ethylene and the HOMO of butadiene. The HOMO of ethylene is symmetric, whereas its LUMO is antisymmetric. This is the opposite for butadiene where its HOMO is antisymmetric and its LUMO symmetric. The HOMO-LUMO pairs must interact and so the formation of the new C-C σ-bonds would give rise to an antisymmetrical MO. From the calculations, the HOMO of the transition state was found to be antisymmetric which means that the reaction is able to occur due to antisymmetrical molecular orbitals in the product. This means that the symmetry of the orbitals remains the same and so is conserved in the reaction. Therefore, HOMO of butadiene (antisymmetric) will interact with the LUMO of ethylene in the reaction to form two new C-C σ-bonds.
References
- ↑ Keiji. Morokuma , Weston Thatcher. Borden , David A. Hrovat. Chair and Boat Transition States for the Cope Rearrangement: A CASSCF Study. J. Am. Chem. Soc., 1988, 110 (13), 4474–4475 DOI:10.1021/ja00221a092
- ↑ University College London. Main Energy Conversion Factors. http://www.ucl.ac.uk/~uccaati/Energy.html
- ↑ Glenn Elert. Distance Between Carbon Atoms http://hypertextbook.com/facts/2001/AliceWarrenGregory.shtml
- ↑ S. S. Batsanov. Van der Waals Radii of Elements. Inorganic Materials. 37, 9, 2001, 871–885