Rep:Mod:SS2510

1C: Catalytic Asymmetric Epoxidation of Alkenes

Part 1: Familiarisation with basic operation technique through set exercises

Conformational analysis using molecular mechanics

The Hydrogenation of Cyclopentadiene dimer

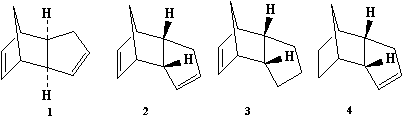
There are two possible products for the dimerisation of cyclopentadiene; the exo(1) and the endo(2). Upon dimerisation of the cyclpentadiene by a Diels-Alder reaction, the endo product is selectively produced, which, after extensive study, became the basis of the Aldor endo rule. Using the Avagadro software program with force field set to MMFF94s, the endo product was shown to have a greater energy (58.31kcal/mol) compared to that of the exo product (55.52kcal/mol) As such the endo is predicted to be less thermodynamically stable and therefore the dimerisation is kinetically controlled. This is confirmed by the literature , which states that for the highest energy transition state, which they term as 7N to form the endo dimer is 21.0kcal/mol, which is 2.9kcal/mol lower than the highest energy transition state of the exo product.

Table of energy calculations of the endo and exo products

Energy type	Endo product (kcal/mol)	Exo product (kcal/mol)
Total Energy	58.31	55.52
Total Bonding Stretch Energy	3.46	3.56
Total Angle Bending Energy	33.37	30.91
Total Torsional Energy	-2.93	-2.92
Total Van Der Waals Energy	12.29	12.99
Total Electrostatic Energy	14.12	13.02

There is an increase in angle bending energy, as there is extra strain on the endo product compared to that of the exo product, as well as increased electrostatic energy due to there being electrostatic repulsion from the hydrogens and the bridging carbon.

When hydrogenating the endo dicyclopentadiene, there are two double bonds, the norbornene (resulting in product 4) and the cyclopentene (product 3). Complete hydrogenation requires prolonged exposure of the dicyclopenatadiene as well as heat, which causes cracking of the dimer, reducing yield .Using the same method as described above, the energies of these molecules were calculated. Product 4 has a calculated energy 9.46kcal/mol lower than that of product 3 and as such is thermodynamically more stable also the hydrogenation to form of molecule 4 with hydrogen + Pd catalyst is several times faster than that of the formation of molecule 3 . The norbornene double bond is longer, suggesting it is weaker than the cyclopentene double bond, and also has larger charge density and a lower bond order. Consequently the norborene double bond is hydrogenated more easily.

Table of energy calculations of molecule 3 and 4

Energy type	Molecule 3 (kcal/mol)	Molecule 4 (kcal/mol)
Total Energy	50.72	41.26
Total Bonding Stretch Energy	3.30	2.82
Total Angle Bending Energy	30.83	24.68
Total Torsional Energy	0.13	-0.38
Total Van Der Waals Energy	13.25	10.64
Total Electrostatic Energy	5.12	5.15

For all energies, with the exception of electrostatic energy, molecule 4 is more stable, suggesting it has stronger bonds, less strain and more favourable van der waals interactions in comparison to that of molecule 3.

Atropisomerism in an intermediate related to the synthesis of Taxol

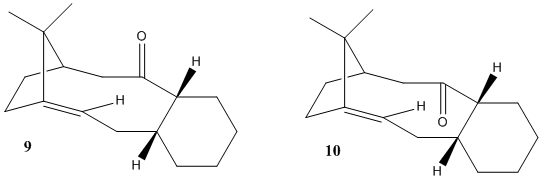
During the synthesis of Taxol, the formation of a key intermediate, molecule 9 and 10, occurs. Molecule 9 and 10 are atropisomers of each other, due to a high energy barrier for the rotation around a single bond from steric effects. There are 4 possible conformers for both 9 and 10, Two chair and two twist boats. Twist boats are always higher in energy than that of chairs and as such when finding the most stable conformer, only chair conformers needs to be considered. While using Avogadro, manual manipulation of molecule was used to form the correct chair conformation and then energy calculations using the MMFF94s forcefield was used.

Table of energy calculations of the most stable conformational form of 9 and 10.

Energy type	Molecule 9 aligned chair (kcal/mol)	Molecule 9 opposite chair (kcal/mol)	Molecule 10 aligned chair (kcal/mol)	Molecule 10 opposite chair (kcal/mol)
Total Energy	82.70	70.55	75.06	60.55

Aligned is defined as the β-carbon at the point of the chair conformation is aligned with the carbonyl group, whereas opposite is when the β-carbon is pointing in the direction opposite of that of the carbonyl group. It was found that the opposite chair for 9 and 10 were the lower energy states and as such more stable.

Table of energy calculations of the most stable forms of molecule 9 and 10 and their polycycloalkane equivalent.

Energy type	Molecule 9 (kcal/mol)	Molecule 10 (kcal/mol)	Saturated Molecule 9 (kcal/mol)	Saturated Molecule 10 (kcal/mol)
Total Energy	70.55	60.55	81.75	71.52
Total Bonding Stretch Energy	7.73	7.58	6.94	6.66
Total Angle Bending Energy	28.31	18.82	32.04	24.74
Total Torsional Energy	0.09	0.16	9.50	8.16
Total Van Der Waals Energy	33.22	33.39	32.71	31.44
Total Electrostatic Energy	0.30	-0.06	0.00	0.00

Thermodynaically, molecule 9 is least stable. There is a far greater angle bending term for 9 than there is for 10. This is due to unfavourable bond angles, which causes increased strain in the molecule. Due to the stereoselective nature of the carbonyl addition, it would be reasonable to suggest that the major product of the addition comes from the addition involving molecule 10.

Hyperstabilised alkenes are those that are less strained than their parent polycycloalkane within molecules containing a bridgehead , resulting in a very slow reaction to functionalise them. One such alkene is present in molecule 9 and 10. The olefin strain energy is smaller in 9 and 10, compared to their parent polycycloalkane and as such are stable. The parent polycycloalkane molecules have substantial amount more angle bending energy and torsional energy, indicating their more strained nature compared to the alkene form.

Spectroscopic Simulation using Quantum Mechanics

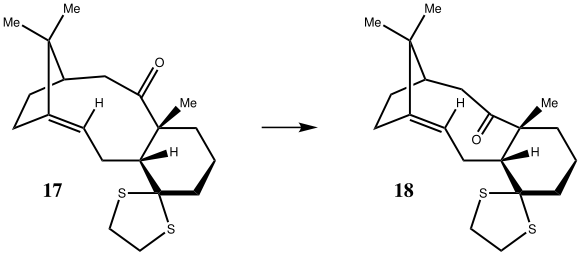
Molecules 17 and 18 are derivatives of 9 and 10. The lowest energy form of these molecules would be the opposite chair conformers, which was discovered from the analysis of 9 and 10. The ¹³ NMR spectra of a molecule can be calculated using Gaussian software package. The key input line used was :

# B3LYP/6-31G(d,p) Opt SCRF=(CPCM,Solvent=???) Freq NMR EmpiricalDispersion=GD3

The solvent used for 17 is chloroform and 18 is benzene. The difference in solvent used is for comparison to the literature. It is important to note that there is need for corrections when calculating the chemical shifts of its NMR due to a spin-coupling errors associated with heavy atoms, in this case sulphur. The exact correction is not know however, but there is a correlation between position in the periodic table and the needed correction. For C-Cl it is -3ppm, and as it is next to S in the table, this correction can be used as an approximation.

¹³C NMR spectra of molecule 17 with opposite chair conformation.

¹³C NMR spectra of molecule 18 with opposite chair conformation.

The spectra that matches that more closely matches the literature ¹³C NMR is that of the 17 opposite and 18 opposite chair conformations.

¹³C NMR spectra of molecule 17 with aligned chair conformation.

¹³C NMR spectra of molecule 18 with aligned chair conformation.

After analysing the NMR spectra of the aligned chair conformation for both, they too do not share the same spectra as the literature states. It is unlikely that the molecules would contain a twist boat conformation as these are far higher in energy. There is, therefore two possibilities, assuming that the molecules have been constructed correctly, either the modelling software has given inaccurate predictions or the literature does not report the correct NMR values. For the majority of the chemical shifts, the calculated values were much lower than the literature. One peak on each spectra, corresponding to the carbon bonded to the two sulphur atoms, is larger for the calculated than the literature value, this can be accounted for the need to correct for large atoms.

Table of NMR spectra values of 17 opposite chair conformation and 18 opposite chair conformation

Peak Assignment	17 Lit (ppm)	17 calculated (ppm)	Chemical shift difference (ppm)	18 Lit (ppm)	18 calculated (ppm)	Chemical shift difference (ppm)
R2C=O	218.79	216.28	2.51	211.49	211.16	0.30
R2C=C	144.63	144.86	0.23	148.72	148.04	0.68
R2C=C	125.33	124.72	0.61	120.90	120.14	0.76
S-CR2-S	72.88	91.35	18.47	74.61	93.74	18.53
R2CCS2	56.19	60.96	4.77	60.53	60.57	0.04
CR3H	52.52	57.08	4.56	51.3	54.87	3.57
CR4	48.50	52.47	3.97	50.94	54.04	3.10
CR4	46.8	51.49	4.69	43.28	49.65	6.37
CR2H2	45.76	46.92	1.15	43.28	49.25	5.97
CH2S2	39.8	43.88	4.08	40.82	46.77	5.95
CR2H2	38.81	41.96	4.07	38.73	42.00	3.27
CR2H2	35.85	41.88	6.03	36.78	41.84	5.06
CR2H2	32.66	35.44	2.78	35.47	38.63	3.16
CR2H2	28.79	31.30	3.01	30.84	33.72	2.88
CR2H2	28.29	28.92	0.63	30.00	28.20	1.80
CR2H2	26.88	28.38	1.95	25.56	26.55	0.99
CRH3	25.66	26.33	0.67	25.35	24.50	0.85
CR2H2	23.86	24.55	0.69	22.21	22.72	0.61
C RH3	20.96	19.78	1.18	21.39	21.68	0.29

The Gibbs free energy was calculated for each isomer and chair configuration, enabling a direct comparison of the relative energies of the molecules.

Table of Gibbs free energy values for molecules 17 and 18

Energy type	Molecule 17	Molecule 18
Opposite chair conformation	-1651.461 kcal/mol	-1651.461 kcal/mol
Aligned chair conformation	-1651.440 kcal/mol	-1651.457 kcal/mol

The Gibbs free energy of the opposite chair conformation are very similar in value, meaning that their thermodynamic stability is very similar. Both the opposite chair conformations are more stable than that of their associated aligned conformations, with the molecule 17 aligned conformation being least stable out of all the conformations.

Part 2: Analysis of the properties of the synthesised alkene epoxides

Crystal structures of the two catalysts

Structure of Shi and Jacobsens catalyst

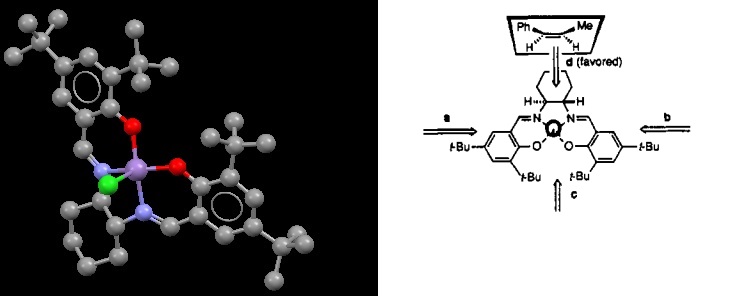
For the epoxidation of alkenes, two catalysts can be used. The Shi catalyst , which has selectivity for trans alkenes , and the Jacobsens catalyst, favouring cis alkenes.

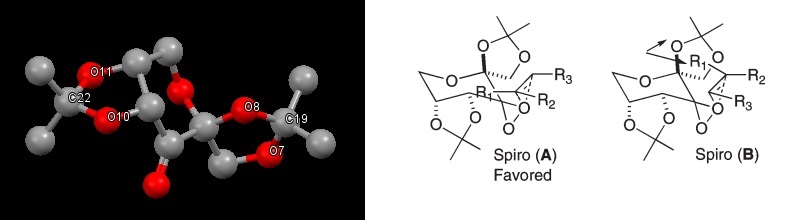
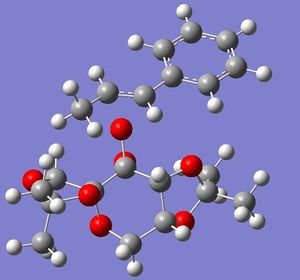
The selectivity of the Shi catalysts comes form the stability of the transition state. There are two forms, called spiral A and spiral B (below). Spiral B is unfavoured due to steric interaction with the dimethyl ketal and the alkene. It is these spiral ketal rings that form which are crucial for the high enantioselectivity for the trans alkenes. There are two anomeric centres in the catalyst. The one located at at C22 has a bond length of 1.42Å with O11 and 1.44Å with O10, for the other at C19, the bond lengths are 1.44Å with O8 and 1.38Å with O7. The difference in bond lengths is possibly due to the anomeric effect. The oxygen located in the ring can hyperconjugate with oxygens 10 and 14, stabilising the molecule. In order for this to happen, a strained orientation must be taken ( although this increase in energy is lower than the stabilisation of the hyperconjugation) resulting in a longer bond. This orientation is what causes the spiral A transition state on the addition of a trans-alkene.

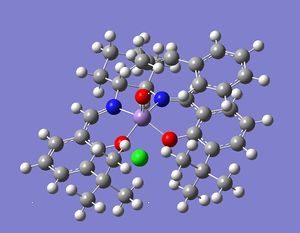
Jacobsens catalyst has 4 possible directions for an cis alkene to attack, labelled a,b,c and d (below). The direction for the attack determines the selectivity. Approach from direction d is the most favoured position to approach as the bulky t-Butyl groups opposite the diimine bridge prevents favourable approach from direction c. The sum Van der Waals radius of the t-Butyl groups is 2.42Å, which shows that there is an attraction between these groups, thus any approach from this direction would have to overcome this interaction. Direction a and b are sterically hindered due to the t-Butyl groups present. As such the most favourable approach is from the direction d.

Calculated NMR of epoxidated alkenes.

The two alkenes to be considered are β-methylstyrene and 1,2-dihydronaphthalene

Using a similar method to that of the intermediates of taxol, the ¹³C NMR of the epoxidated β-methylstyrene and 1,2-dihydronaphthalene can be computed. The NMR does not provide data on absolute configurations however it does enable us to check that the computations match experimental data. For β-methylstyrene oxide two spectra was computed however for 1,2-dihydronaphthalene oxide, only one spectra is expected as due to its locked structure, only RS and SR chiral structures

¹³C NMR taken for the (R S)1,2-dihydronaphthalene

¹³C NMR taken for the (S S)beta-methylstyrene

¹³C NMR taken for the (S R)beta-methylstyrene

¹³C NMR values of (R S)1,2-dihydronaphthalene oxide

Assigned peaks	Chemical shift of RS Lit (ppm)	Chemical shift of RS Calculated(ppm)	Difference in shifts(ppm)
Aromatic CR3	137.1	135.4	1.7
Aromatic CR2H	132.9	130.4	2.5
Aromatic CR2H	129.9	126.7	3.2
Aromatic CR2H	129.8	123.9	5.9
Aromatic CR2H	128.8	123.5	5.3
Aromatic CR2H	126.5	121.7	4.8
epoxide COR2H	55.5	52.8	2.7
epoxide COR2H	53.2	52.2	1.0
Alkane CR1H2	24.8	30.18	4.32
Alkane CR1H2	22.2	29.1	6.9

For the NMR of (R S)1,2-dihydronaphthalene oxide is similar to the literature however there is a need for a correction formula to correct for some of the chemical shift differences, especially for the aromatic ring.

¹³CNMR values of (S S)β-methylstyrene oxide

Assigned peaks	Chemical shift of RS Lit (ppm)	Chemical shift of RS Calculated(ppm)	Difference in shifts(ppm)
Aromatic CR3	137.7	132.8	4.9
Aromatic CR2H	128.3	123.4	4.9
Aromatic CR2H	127.9	123.1	4.8
Aromatic CR2H	126.5	122.7	3.8
Aromatic CR2H	N/a	122.4	N/a
Aromatic CR2H	N/a	121.4	N/a
epoxide COR2H	59.4	59.0	0.4
epoxide COR2H	58.9	57.7	1.2
Alkane C/sub>H3	17.8	13.1	4.7

¹³CNMR values of (S R)β-methylstyrene oxide

Assigned peaks	Chemical shift of RS Lit (ppm)	Chemical shift of RS Calculated(ppm)	Difference in shifts(ppm)
Aromatic CR3	135.5	132.8	2.7
Aromatic CR2H	127.9	123.4	4.5
Aromatic CR2H	127.4	123.1	4.3
Aromatic CR2H	126.5	122.7	3.8
Aromatic CR2H	N/a	122.4	N/a
Aromatic CR2H	N/a	121.4	N/a
epoxide COR2H	57.5	59.0	2.5
epoxide COR2H	55.0	57.7	2.7
Alkane CH3	12.5	13.1	0.6

There are two peaks visible in both β-methylstyrene oxide spectra not recorded in literature. The most likely explanation is that there are in fact 5 different carbon environments in the benzene ring ( excluding the substituted carbon) however due to some of these having a very similar chemical shift, at high temperatures, these peaks may average out, forming one peak.

Assigning the absolute configuration of the product

The absolute configuration can be assigned of a molecule can be assigned by three ways, simply checking the literature for rotation, measuring properties of the molecule or using calculated properties of transition states.

The three measurements that can be taken to determine the configuration of a molecule, they are; the optical rotation, the electronic circular dichroism (ECD) and the vibrational circular dichroism (VCD). Epoxides contain no chromophore and as such, any value computed for the ECD would be meaningless. Unfortunately VCD is a rather new technique and as such there is very little data available. The main way of determining configuration is by measuring the optical rotation.

Optical rotation values of 1,2-dihydronaphthalene oxide

Configuration	Optical rotation lit (o)	Optical rotation computed (o)
(SR)	-39	-35.9
(RS	129	35.9

Optical rotation values of beta-methylstyrene oxide

Configuration	Optical rotation lit (o)	Optical rotation computed (o)
(SR)	40.51	38.6
(RS	-37.8	-37.59
(SS)	-41.8	-37.49
(RR)	44.3	37.5

All calculated optical rotation data matches those quoted in the literature, except for the OR of (RS)1,2-dihydronaphthalene oxide however it is the polarity of the number that is most important, and it is the opposite of its inverted configuration (SR)

Although there is a lack of literature data on VCD, they do provide mirror images on spectra for opposite configurations, making them potentially very useful in the future.

VCD taken form the (S R)beta-methylstyrene oxide

VCD taken form the (S R)beta-methylstyrene oxide

By taking the lowest transition states for the shi and jacobsens catalysts, the enantiomeric excess can be calculated. By using the equation ΔG=-RTlnk, where G is free energy, R is the gas constant, T is temperature (298K) and k is the ratio of concentration of the two enantiomers. After obtaining k it can be substituted into the equation k=[A]/[B] ( in this case the free energy of B was subtracted from A). As this is a ratio it must add to 1, therefore [A]+[B]=1. By substituting [A], we get the equation [B]=1/k+1.

Types of Transition states.

Shi catalyst with Endo RR)	Shi cataylst with Exo SS
Jacobsen's catalyst with Exo SR	Jacobsen's catayst with Exo RS

Enantiomeric excess in the Shi catalyst transition state.

Lowest energy RR conformation (kJ/mol)	Lowest energy SS conformation (kJ/mol)	ΔG (kJ/mol)	k	% RR	% SS
3526131.68	-3526111.46	-20.22	3514.77	99.97%	0.03%

Enantiomeric excess in the Shi catalyst transition state.

Lowest energy SR conformation (kJ/mol)	Lowest energy SR conformation (kJ/mol)	ΔG (kJ/mol)	k	% SR	% RS
8882747.97	-8882725.66	-22.31	8190.94	99.99	0.01%

By using the free energy, the computation predicts that there will be an enantiomers excess of RR at 99.97% for the Shi catalyst and a 99.99% excess in the SR enantiomer for the Jacobsens catalyst. Comparing these values to literature, it is found that, indeed for the Shi catalyst there is an excess of 90%, achieved due to the formation of spiral A. For jacobsen catalyst, the predicted excess is 92% for SR. There is a slight over estimation using this method, however it does correctly predict the correct the enantiomer for both catalysts.

Investigating the non-covalent interactions in the active-site of the reaction transition state

The NIC interactions in the Shi transition state with lowest energy RR

Above is a a rendering of the Shi catalyst during its transition state with the lowest energy RR endo enatiomer. Non-covalent interactions have been calculated and shown as surfaces. The different colour of these surfaces represents the strength of interactions. Between the carbons of the alkene section of the beta-methylstyrene and the anomeric oxygens, there are strong attractive interactions. These attractive interactions would only be able to form when the alkene and the catalyst have the correct configuration, i.e, when the alkene is endo and the correct dioxirane positions. The result of these interactions means that the transition state is stabilised, which would not be present in other configurations. In addition to these intermolecular interactions, there are also nonbonding interactions intramolecularly within the Shi cataylst. These most notably occur between the anomeric centres and the branching alkanes, as well as between the transition state ketone and the cyclic groups adjacent. There is a multicoloured ring located between the transition state ketone and the alkene. This represents the transition state between the two, which results in the spiral discussed earlier.

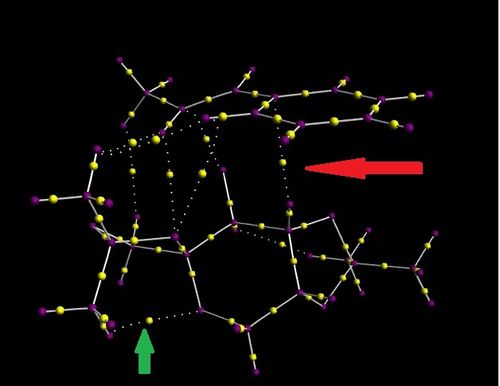
Investigating the Electronic topology (QTAIM) in the active-site of the reaction transition state

The Electronic topology of the Shi catalyst and RR-beta-methylstyrene.

[[

The QTAIM technique is complimentary to that of the electron density. It identifies the bond critical point for both covalent and NIC interactions. The yellow dots represent the bond critical point, the purple dots are atoms, white lines are bonds and dashed lines are NIC's. The bond critical point appears to be closer to that of the less electronegative atom involved in the bonding, this can be seen with the BCP being closer to the hydrogens than that of the carbons within the methyl groups and the the BCP being closer to the carbon in the ketone bond. The consequence of this positioning is the first derivative of the electron density to equal zero. An example of an intramolecular ineraction is pointed out by the green arrow. It is an attractive interaction between a carbon and a hydrogen. The bond critical point is closer to the hydrogen's position however, it is not as close as have been observed with covalent bonds. The weaker the interaction, the more centralised the bond critical bond. The red arrow, indicatign a bond critical point between a hydrogen on the Shi catalyst and the beta-methylstyrene also shows that the point is closer to that of hydrogen, however not as close as it would otherwise be in a formal bond.