The aim of this computational experiment was to model and characterize the structure of the transition state of the Cope Rearrangement and Diels-Alder Reaction. Once the transition state had been obtained the activation energies of the reactions were determined and compared to experimental values. For the Diels-Alder reaction the computational activation energies and the MO diagrams were used to explain the regioselectivity of the reaction.

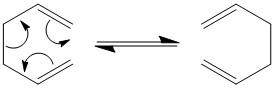
Cope Rearrangement

1,5-hexadiene

1,5-hexadiene undergoes the cope rearrangement, this is an example of a [3,3] sigmatropic rearrangement and is shown below.

1,5-hexadiene can have multiple different conformations due to free rotation around the sp³C-sp³C bond, the two lowest energy conformations are anti-periplanar(app) and gauche. APP is when the two carbon substituents are at 180° to each other, and gauche is when the two carbon substituents are at 60° to each other. Each of the app and gauche conformations can more than one conformation due to the relative orientation of the two alkene groups.

This computational exercise aims to determine the lowest energy conformer of 1-5-hexadiene and to model the transition sate of the Cope Rearrangement. This will allow the lowest energy transition state to be determine and consequently the preferred reaction mechanism.

Between the app and gauche conformation of 1,5-hexadiene, it is expected that the app conformation will be the lowest in energy due to it being the least sterically hindered. The app conformation which is expected to be the lowest in energy is the one with the alkene groups parallel to each other, anti 1, another low energy app conformation is anti 2. For the gauche conformations it is expected that the lowest energy form is gauche 3.^[1]

The Hartree-Fock basis set works by taking the average of the exchange energies of a molecule over all electronic wavefunctions. This results in a simple expression for the average potential field of a molecule from which physical quantities can be determined.^[2] The electronic energies and the point group of the three conformations of 1,5-hexadiene above were calculated using the Hartree-Fock/3-21G basis set.

HF/3-21G basis set (Hartree)
	Point Group	Energy
Anti 1	C2	-231.69260	LOG File
Anti 2	C_i	-231.69254	LOG File
Gauche 3	C1	-231.69266	LOG File

As can be seen from the above table the gauche conformation is the lowest energy conformer, however it is known that the app conformation is lower in energy due to less steric strain in the ring. A reason for the HF/3-21G basis set giving the gauche conformer as the lowest in energy is due to the Hartree-Fock method not including any electron correlation, therefore many electronic effects may not be considered e.g. CH-π interactions.^[1] For this reason the energetic energies were calculated again but with using a basis set that had uses a higher level of theory, the B3LYP/6-31G* basis set.

The B3LYP/6-31G* method is a hybrid method which uses a mixture of Hartree-Fock methods as detailed above and Density Functional methods (DFT). In the DFT method the exact exchange energies from the HF method are replaced with a more general expression which includes terms which account for both the exchange and electron correlation energies. This higher level of theory gives a more accurate representation of the molecule and its physical characteristics.^[3]

HF/3-21G vs B3LYP/6-31G* (Hartree)
	HF/3-21G	B3LYP/6-31G*	B3LYP Log File
Anti 1	-231.69260	-234.61180	LOG File
Anti 2	-231.69254	-234.61170	LOG File
Gauche 3	-231.69266	-234.61133	LOG File

The relative electronic energies of the conformations of 1,5-hexadiene agrees with those reported by Schaefer et al. when a higher level of theory is used.^[1] The reason for the relative energy differences between the data values for the two methods is that the HF method takes an average of all of the exchange energies whereas the B3LYP method takes into account the electron correlation energies as well i.e. it factors in electron-electron interaction energies. Therefore electron interactions such as CH-π between the vinyl and the CH are not factored in, which is why using the HF method the gauche conformer is lower in energy.

All of the energies that have so far been calculated are the energies of the bare potential energy surface. In order to obtain energies which can be compared to experimental values addition terms must be factored in order to do this a frequency calculation must be run. These results of these calculations are shown in the table below.

Thermodynamic energies (kcal/mol)
	Calculated (B3LYP/6-31G*)
	Sum of electronic and zero point energies	Sum of electronic and thermal energies
Anti 1	-147131.59	-147126.99	LOG File
Anti 2	-147131.54	-147126.92	LOG File
Gauche 3	-147131.22	-147126.68	LOG File

1 hartree = 627.509 kcal/mol

The thermodynamic properties of the above conformations of 1,5-hexadiene were not calculated at 0 K as the energy values obtained will be the same as the sum of the electronic and zero point energies, as shown in the above calculations. This is due to at 0 K there will be no thermal energy or entropy contribution towards the thermal energy, enthalphy or free energy.

Transition State Structures

The structure of the transition state can be optimized by several different methods;

By computing the force constant at the beginning of the calculation.
Using the redundant co-ordinate editor.
Using QST2, specifying the reactant and product and calculating the TS structure between them.

These three methods will be used to model the chair and boat transition states for the cope rearrangement. The Intrinsic Reaction Co-ordinate (IRC) will also be used to determine the conformation of 1,5-hexadiene which the transition states will lead to. Finally the activation energy of the chair and boat transition states will be calculated.

To confirm that the structure obtained for the transition state is in fact the transition state the vibrations of the molecule will be calculated. If the structure obtained from the optimization is a minimum on the potential energy surface then all of the vibrations will be positive due to the eigenvalues of the force constant matrix all being positive therefore giving a positive vibration. If the structure obtained is the transition state then there will be one and only one negative vibration, which is due to this point on the potential energy surface being a maximum, therefore giving a negative force constant and hence an imaginary vibration. The equation which links the force constants and the vibrational frequencies of the molecule is shown below. ^[4]

ν = \frac{1}{2 π} \sqrt{\frac{k}{μ}}

Where;

ν = vibrational frequency

k = force constant

μ = reduced mass

Chair Transition Structure

The chair transition state was optimized by computing the force constant at the beginning of the calculation. To do this an allyl fragment was optimized using the HF/3-21G basis set to obtain one half of the transition state, two of the optimized allyl fragments were orientated in a chair conformation and the terminal carbons were placed approximately 2.2 Å apart. This guessed chair transition state structure can now be optimized using two methods.

The first method is to calculate the force constant at the beginning of the calculation, by optimizing the guessed chair conformation to a TS (berry) and calculating the force constant just once. The frequency calculation gave an imaginary vibration at -818cm^-1 which corresponds to the cope rearrangement and is shown below. (LOG File)

Pentahelicene

The second method is to use the redundant co-ordinate editor in which certain atoms are frozen and optimizing the rest of the structure. The reaction co-ordinate (terminal carbons) are frozen and the rest of the molecule is optimized to a minimum, the reaction co-ordinate is then unfrozen and the the transition structure is minimized. This gave an imaginary vibration at 818cm^-1 which again corresponds to the vibration due to the cope rearrangement and is shown below. (LOG File)

Pentahelicene

Boat Transition Structure

The boat transition structure was optimized using the QST2 method. To do this the reactants and products are specified and then the calculation will interpolate between the two structures to obtain the transition state. The reactants and products had to be manually numbered so that once the rearrangement occurred the atoms corresponded to the equivalent atoms in the reactant. The reactant that was used was the optimizes anti 2 structure from the first section. The QST2 calculation was then set up to optimize to a transition state. Initially the calculation failed due to the anti 2 arrangement being to far away from the boat transition state, therefore the reactants and products were manually adjusted to adopt a boat like structure and the minimization was run again. This gave the boat transition structure as shown below which had an imaginary vibration at -840 cm^-1 which corresponded to the cope rearrangement. (LOG File)

Pentahelicene

Intrinsic Reaction Coordinate

The intrinsic reaction coordinate (IRC) method is used to calculate which conformation of 1,5-hexadiene the transition structure will lead to. It does this by creating a series of points by making small changes to the geometry of the molecule in the direction where the gradient of the potential energy surface is the steepest. The transition state structure was determined by running an IRC job in the forward direction only, due to the reaction coordinate being symmetrical. the force constants of the reaction were calculated at every step of the reaction, and the number of points along the IRC was set to 50.

For the chair transition structure the IRC calculation resulted in a gauche conformation, which once minimized corresponded to the gauche 2 conformation of 1,5-hexadiene. (IRC LOG File, Minimization LOG File)

For the boat transition structure the Initial IRC calculation had not reached a geometry from which the structure could be minimized. The IRC was therefore restarted but with the number of points set to 500, this then resulted in a structure which was minimized to the gauche 3 conformation of 1,5-hexadiene. (IRC LOG File, Minimization LOG File)

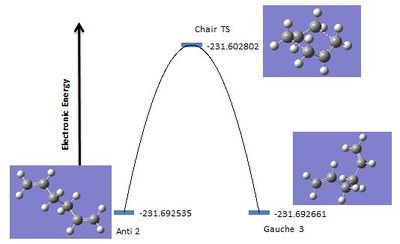
Activation Energies

To calculate the activation energies of the reaction via the boat and chair transition state the transition states were optimized to a minimum using the B3LYP/6-31G* basis set and then a frequency calculation was carried out to obtain the thermodynamic data. For the boat transition state when an optimization using the B3LYP/6-31G* basis set was initially done a distortion from the transition occurred. To overcome this the reactant co-ordinates (sp² terminal carbons) were frozen an optimization was run, which was followed by another minimization without the reactant coordinated frozen using the B3LYP/6-31G* basis set.

Summary of Transition State energies (Hartree)
	HF/3-21G (hartree)			B3LYP/6-31G* (hartree)
	Electronic Energy	Sum of electronic and zero point energies (0 K)	Sum of electronic and thermal energies (298 K)	Electronic Energy	Sum of electronic and zero point energies (0 K)	Sum of electronic and thermal energies (298 K)
Chair TS	-231.61932	-231.46670	-231.46134	-234.55698	-234.41493	-234.40901	HF LOG File, B3LYP LOG File
Boat TS	-231.60280	-231.45092	-231.44529	-234.54309	-234.40234	-234.39600	HF LOG File, B3LYP LOG File
Reactant (Anti 2)	-231.69254	-231.53954	-231.53257	-234.61170	-234.46921	-234.46186	HF LOG File, B3LYP LOG File

1 hartree = 627.509 kcal/mol

Summary of Activation energies (Kcal/mol)
	HF/3-21G		B3LYP/6-31G*		Experimental ^[5]
	0 K	298 0 K	0 K	298 K	Experimental ^[5]
ΔE^‡ (Chair)	45.71	44.70	34.06	33.16	33.5
ΔE^‡ (Boat)	55.61	54.77	41.96	41.33	39.2
(Boat - Chair) ΔE^‡	9.90	10.07	7.90	8.17	5.7

As can be seen from the summary of activation energies above there is a very close agreement between the calculated activation energy using the B3LYP/6-31G* basis set and the experimental activation energy, with only a 0.34 kcal/mol difference (at 298 K). This shows that the B3LYP/6-31G* basis set is a very good approximation to the actual transition state. However for the boat transition state there is a greater difference between the calculated and experimental values. The energy difference between the boat and chair transition state according to Gajewski is 5.7 kcal/mol, however as can be seen above there is still quite a large difference between the chair and boat transition states, this is mainly due to the difference between the calculated boat transition state and the experimental value.

Diels-Alder Cycloaddition

Molecular Orbitals

The structure of cis-butadiene was optimized using first the HF/3-12 basis set and then the B3LYP/6-31G* basis set to obtain the optimized structure. The HOMO and LUMO of cis-butadiene were then visualized and are shown below.

The HOMO of cis-butadiene is asymmetric with respect to the plane of reflection, and the LUMO of cis-butadiene is symmetric with respect to the plane of reflection.

Transition State

The transition state of the Diels-Alder cycloaddition was obtained by specifying the reactants and products of the Diels-Alder reaction, then using the QST2 method to interpolate between them to obtain the transition state. To obtain the reactant cis-butadiene and ethene were both optimized using the HF/3-21G basis set. The cis-butadiene and ethene were orientated so that the ethene was above cis-butadiene, with the distance between the terminal carbons of cis-butadiene and ethene being approximately 2.2 Å as reported by Houk et al.^[6] The structure for the transition state is shown below. An IRC calculation was carried out to confirm the transition state obtained above was the transition state that links the reactants (cis-butadiene and ethene) with the product of the reaction (cyclohexene). Due to the reaction not being symmetrical the calculation was run in both directions, the force constants were calculated at every step and the number of iterations was 100.

Pentahelicene

Carbon-Carbon Bond Lengths (nm)
Bond	Distance
sp³-sp³	0.153 ^[7]
sp²-sp²	0.135 ^[7]
VdW radii	0.170 ^[8]
DA TS partially formed bonds	0.221

The bond length of the partially formed C-C bond in the transition state of the reaction of cis-butadiene and ethylene is 0.221 nm. The van der Waal radii of carbon is 0.170 nm, therefore the carbons between which the new σ-bonds are going to form are within the each others van der Waals radii so there is going to be an attractive force between them. The carbons are not close enough to formally acknowledge this as a bond, as the C-C distance between two sp³ hybridized carbons is 0.153 nm. However when the vibration from the transition state is examined it can be seen that the vibration brings the terminal carbons much closer together, this shortening of the C-C bond will eventually lead to the formation of the sp³-sp³ C-C bonds in the product.

The lowest positive vibration in the transition state occurs at 167 cm^-1, this positive vibration corresponds to a stationary point on the potential energy surface (a minimum), which results in a positive force constant and hence vibration. The vibration at -819 cm^-1 corresponds to the only point on the potential energy surface where the energy is a maximum in one direction and a minimum in the other which results in a negative force constant and hence an imaginary vibration, which is due to it corresponding to the transition state of the molecule. Therefore the vibration at -819 cm^-1 corresponds to the synchronous formation of the two new σ sp³-sp³ C-C bonds to give cyclohexene, which can also be seen by observing the movie of the vibration below. Whereas the vibration at 167 cm^-1 is asynchronous and does not correspond to the formation of the two new σ sp³-sp³ C-C bonds.^[4]

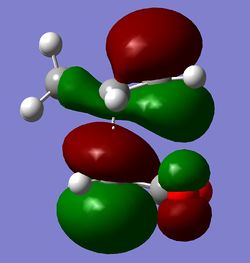
The HOMO of the transition state is shown below and corresponds to the LUMO of cis-butadiene and the HOMO of ethylene as shown below. The LUMO of cis-butadiene and the HOMO of ethylene are both symmetric with respect to the plane, therefore the resulting HOMO from the combination of these two orbitals is asymmetric with respect to the plane of symmetry. When two new σ bonds are formed they can be formed both on the same face of the π system (suprafacial) or from opposite faces of the π system (antarafacial). This reaction is a 4n + 2 pericyclic reaction which is promoted by heat, for it to be allowed it must have one suprafacial component. As can be seen from the HOMO of the TS the two new σ bonds are both formed on the same face of the п system, hence having a suprafacial component therefore making this reaction an allowed pericyclic process.

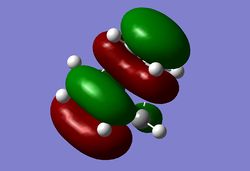The transition state obtained above was optimized using the HF/3-21G and then the B3LYP/6-31G* basis set to obtain the thermodynamic data values outlined below.

Summary of Transition State energies (Hartree)
	HF/3-21G (hartree)			B3LYP/6-31G* (hartree)
	Electronic Energy	Sum of electronic and zero point energies (0 K)	Sum of electronic and thermal energies (298 K)	Electronic Energy	Sum of electronic and zero point energies (0 K)	Sum of electronic and thermal energies (298 K)
Diels-Alder TS	-231.72037	-231.56319	-231.55775	-234.63915	-234.49262	-234.48762	HF LOG File, B3LYP LOG File
Reactant	-231.65792	-231.50991	-231.50052	-234.57278	-234.43496	-234.42952	HF LOG File, B3LYP LOG File

1 hartree = 627.509 kcal/mol

Summary of Activation energies (Kcal/mol)
	HF/3-21G		B3LYP/6-31G*		Experimental
	0 K	298 0 K	0 K	298 K	Experimental
ΔE^‡ DA TS	33.43	35.91	36.18	36.46	34.3 ^[6]

As can be seen from the above activation energy data there is a close agreement between the calculated and experimental values. This indicates that the optimized structure is very similar to the real transition state, in fact using the lower level of theory HF basis set gave a value for the optimized transition state which is closer in energy to the experimental value. Due to the transition state being a maximum on the potential energy surface when the transition state was optimized it may in fact have optimized the structure so it is not quite the highest energy point when the B3LYP/6-31G* basis set was used, which could be a reason for the slight difference between the calculated and experimental values.

Regioselectivity

Cyclohexa-1,3-diene and maleic anhydride undergo a very rapid Diels-Alder reaction as shown below, the endo adduct is predominantly formed. It is thought that this reaction is under kinetic control, so the transition state which gives the lowest activation energy will give the product in excess.

To determine whether this is a kinetically or thermodynamically controlled reaction the energy of the transition state needed to be calculated. The structure of the transition state was determined using the same method as detailed above for the Diels-Alder transition state; interpolation between the reactant and product using the QST2 basis then calculating the IRC in both directions with the force constant calculated every step (IRC Endo LOG File, IRC Exo LOG File).

Exo TS =
LOG File

Exo TS

Endo TS =
LOG File

Endo TS

In the endo transition state maleic anhydride is orientated above the diene fragment of cyclohexadiene, whereas in the exo transition state the maleic anhydride is orientated over the alkyl fragment of cyclohexadiene. In the endo transition state the -(C=O)-O-(C=O)- fragment of maleic anhydride is above two sp² hybridized carbons, whereas in the exo transition state the same maleic anhydride fragment is above two sp³ hybridized carbons. Consequently in the endo transition state the carbons in the -(C=O)-O-(C=O)- maleic anhydride fragments are 0.297 nm away from the hydrogen below them, but in the exo transition state they are much closer to a hydrogen and at only 0.243 nm away. The van der Waals radius for a C-H bond is 0.270 nm, therefore in the exo transition state the C-H interaction above is much closer than this which will lead to steric repulsion between the two atoms, whereas in the endo transition state the C-H distance is much longer than the van der Waals distance so there will be significantly less steric repulsion.

It can also be seen from the transition structures above that the partially formed σ bonds are slightly shorter in the endo than the exo transition state. The steric repulsion detailed above could be responsible for this difference in bond lengths, as in the exo transition state the two reactants are positioned slightly further apart in order to minimize the steric repulsion. Which leads to slightly longer partially formed σ bonds in the exo transition state therefore causing the transition state to be higher in energy.

Summary of Activation energies (Kcal/mol)
	HF/3-21G		B3LYP/6-31G*		Experimental ^[6]
	0 K	298 0 K	0 K	298 K	Experimental ^[6]
ΔE^‡ (Endo)	27.08	25.55	19.96	20.49	12.7
ΔE^‡ (Exo)	31.33	29.82	22.47	23.00	12.7

Relative energies of Products (Kcal/mol)
	HF/3-21G		B3LYP/6-31G*
	0 K	298 0 K	0 K	298 K
ΔE Endo Product	39.58	41.51	25.44	25.37
ΔE Exo Product	32.37	39.79	23.69	23.73

As can be seen from the summary of activation energies above the transition state which leads to the endo adduct has a lower activation energy using both the HF/3-21G and B3LYP/6-31G* basis sets, therefore confirming the endo product is the kinetic product. Previous work by Fox et al. has found in Diels-Alder reactions with maleic anhydride as the dieneophile, that the exo product is always the thermodynamic product.^[9] However as can be seen from the relative energies of the products, the endo product is lower in energy than the exo product, so for the above calculation the endo product is both the kinetic and thermodynamic product. When the relative energy of the product was calculated with the HF/3-21G basis set and then the B3LYP/6-31G* basis set the energy difference decreased. If the energy difference was calculated with a basis set at a higher level of theory than B3LYP/6-31G* the relative energy values may change so that the exo adduct is lowest in energy and therefore the thermodynamic product, this was not done however as it is computationally expensive, but could be an area for further work.

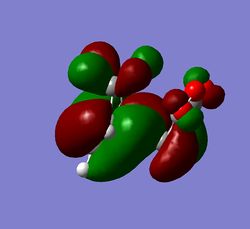
The HOMO of both the endo and exo transition state is due to a combination of the cyclohexadiene HOMO and the maleic anhydride LUMO, a simplified 'cartoon' version of the HOMO for both adducts is also shown. Between the -(C=O)-O-(C=O)- fragment of maleic anhydride and the rest of the transition state there is a nodal plane which is seen as the p orbital on the carbonyl oxygen being in a different phase to the p orbitals on the dieneophile carbons. In the exo TS HOMO the nodal plane is more clearly defined which is due to the maleic anhydride not being orientated under the diene, this more clearly defined node indicates there is a greater antibonding interaction than in the endo TS HOMO, which agrees with the relative energies of the transition states. Another consequence of the maleic anhydride dieneophile being orientated underneath the cyclohexadiene in the endo adduct is that the p orbitals in the LUMO of the maleic anhydride interacts with the HOMO of cyclohaxadiene to convey stability to the transition state of the endo adduct. This interaction is called the secondary orbital overlap effect, and can also be seen to a much greater extent in the endo HOMO-1 (below).^[10]

Other interactions that are worthy of note are there is a nodal plane down the center of the transition state for both the endo and exo forms. This indicates that in the transition state the new π bond found in the product has not yet started to form, therefore the transition state occurs early on in the reaction coordinate. Another interesting observation is that the sp³ hybridized carbons in cyclohexadiene becomes almost p orbital like except they are not linear, a reason for this is the constrained geometry in the ring does not sterically favor sp³ hybridized orbitals.

References

↑ ^1.0 ^1.1 ^1.2 Rocque B. G., Gonzales J. M., *Schaefer III H. F. , Mol. Phys., 2002, 100 (4), 441. DOI:10.1080/00268970110081412
↑ *Slater J.C., Phys. Rev., 1951, 81 (3), 385. DOI:10.1103/PhysRev.81.385
↑ Kohn W.,Sham L. J., Phys. Rev., 1965, 140 (4A), A1133. DOI:10.1103/PhysRev.140.A1133
↑ ^4.0 ^4.1 Jensen F., 'Introduction to Computational Chemistry', John Wiley & Sons, 2007, 432, 2nd, England.
↑ Gajewski J. J., Conrad N. D., J. Am. Chem. Soc., 1979, 101(22), 6693. DOI:10.1021/ja00516a035
↑ ^6.0 ^6.1 ^6.2 Storer J. W., Ralmondi L., *Houk K. N. , J. Am. Chem. Soc., 1994, 116(21), 9675. DOI:10.1021/ja00100a037 Cite error: Invalid <ref> tag; name "DA distances" defined multiple times with different content
↑ ^7.0 ^7.1 Lide Jr. D. R. , Tetrahedron, 1962, 17(3-4), 125. DOI:10.1016/S0040-4020(01)99012-X
↑ Bondi A. , J. Phys. Chem., 1964, 68(3), 441. DOI:10.1021/j100785a001
↑ Fox M*. A, Cardona R., Kiwiet N. J., J. Org. Chem., 1987, 52, 1469. DOI:10.1021/jo00384a016
↑ Fleming I., 'Molecular Orbitals and Organic Chemical Reactions', John Wiley & Sons, 2009, 235, England.

[1,5-hexadiene_config-1] 1.0 ^1.1 ^1.2 Rocque B. G., Gonzales J. M., *Schaefer III H. F. , Mol. Phys., 2002, 100 (4), 441. DOI:10.1080/00268970110081412

[HF_REVIEW-2] *Slater J.C., Phys. Rev., 1951, 81 (3), 385. DOI:10.1103/PhysRev.81.385

[DFT_REVIEW-3] Kohn W.,Sham L. J., Phys. Rev., 1965, 140 (4A), A1133. DOI:10.1103/PhysRev.140.A1133

[imaginary_vibrations-4] 4.0 ^4.1 Jensen F., 'Introduction to Computational Chemistry', John Wiley & Sons, 2007, 432, 2nd, England.

[Cope_activation_energies_2-5] Gajewski J. J., Conrad N. D., J. Am. Chem. Soc., 1979, 101(22), 6693. DOI:10.1021/ja00516a035

[DA_distances-6] 6.0 ^6.1 ^6.2 Storer J. W., Ralmondi L., *Houk K. N. , J. Am. Chem. Soc., 1994, 116(21), 9675. DOI:10.1021/ja00100a037 Cite error: Invalid <ref> tag; name "DA distances" defined multiple times with different content

[C-C_lengths-7] 7.0 ^7.1 Lide Jr. D. R. , Tetrahedron, 1962, 17(3-4), 125. DOI:10.1016/S0040-4020(01)99012-X

[VdW_distances-8] Bondi A. , J. Phys. Chem., 1964, 68(3), 441. DOI:10.1021/j100785a001

[DA_thermo_vs_kinetic-9] Fox M*. A, Cardona R., Kiwiet N. J., J. Org. Chem., 1987, 52, 1469. DOI:10.1021/jo00384a016

[2°_orbital_overlap-10] Fleming I., 'Molecular Orbitals and Organic Chemical Reactions', John Wiley & Sons, 2009, 235, England.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]